32.1投影同步课时训练(Word版 含答案)
文档属性
| 名称 | 32.1投影同步课时训练(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 275.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览



文档简介
32.1投影同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
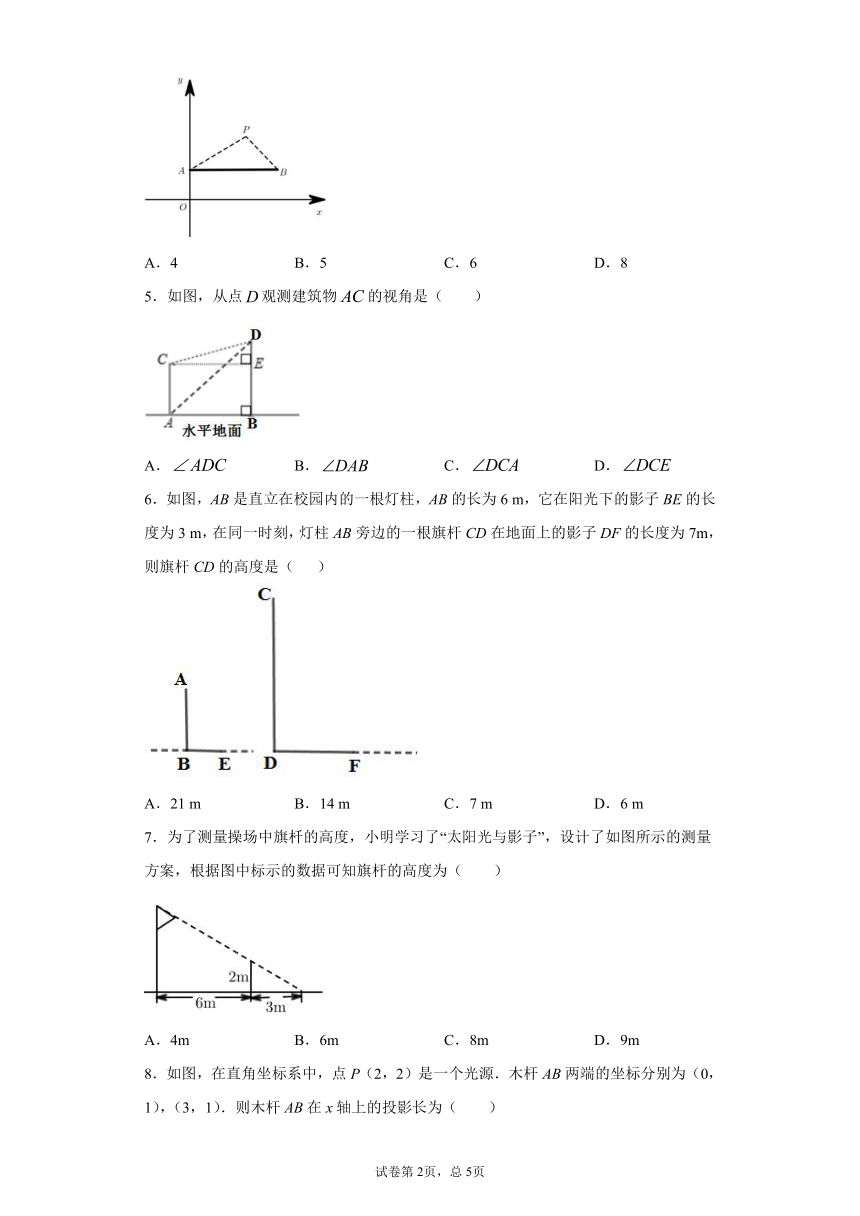
1.在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上他行走在这条路上如图,当他从点走到点的过程,他在灯光照射下的影长与所走路程的变化关系图象大致是( )
A. B. C. D.
2.如图,晚上小明在路灯下沿路从处径直走到处,这一过程中他在地上的影子( )
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
3.在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下( )
A.不能够确定谁的影子长 B.小刚的影子比小红的影子短
C.小刚跟小红的影子一样长 D.小刚的影子比小红的影子长
4.如图,在平面直角坐标系中,点是一个光源.木杆AB两端的坐标分别为,.则木杆AB在x轴上的投影长为( ).
A.4 B.5 C.6 D.8
5.如图,从点观测建筑物的视角是( )
A. B. C. D.
6.如图,AB是直立在校园内的一根灯柱,AB的长为6 m,它在阳光下的影子BE的长度为3 m,在同一时刻,灯柱AB旁边的一根旗杆CD在地面上的影子DF的长度为7m,则旗杆CD的高度是( )
A.21 m B.14 m C.7 m D.6 m
7.为了测量操场中旗杄的高度,小明学习了“太阳光与影子”,设计了如图所示的测量方案,根据图中标示的数据可知旗杆的高度为( )
A.4m B.6m C.8m D.9m
8.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3 B.5 C.6 D.7
9.身高米的小明同学利用相似三角形测量学校旗杆的高度,上午点,小明在阳光下的影长为米,此时测得旗杆的影长为米,则学校旗杆的高度是( )
A.米 B.米 C.米 D.米
10.如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
二、填空题
11.晚上行走时,当你离路灯越近时,你的影子就越短.(______)
12.张三和李四并排站立在阳光下,张三身高1.80米,他的影长2.0米,李四比张三矮9厘米,此时李四的影长是___米.
13.如图,一棵树(AB)的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE)为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多可以离开树干多少米才可以不被阳光晒到?____.
14.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成角时,第二次是阳光与地面成角时,两次测量的影长相差8米,则树高______米.(结果保留根号)
15.如图,小明在A时测得旗杆的影长是2米,B时测得旗杆的影长是8米,两次的日照光线恰好互相垂直,则旗杆的高度是______米.
16.在某一时刻,测得一根长为1.5m的标杆的影长为3m,同时测得一根旗杆的影长为16m,那么这根旗杆的高度为_______m.
三、解答题
17.如图,小明与同学合作利用太阳光线测量旗杆的高度,身高的小明()落在地面上的影长.
(1)请画出旗杆在同一时刻阳光照射下在地面上的影子.
(2)若小明测得此刻旗杆落在地面上的影长,求旗杆的高度.
18.晚上,小亮在广场乘凉,图中线段表示站立在广场上的小亮,线段表示直立在广场上的灯杆,点表示照明灯.
(1)请你在图中画出小亮在照明灯照射下的影子(请保留作图痕迹,并把影子描成粗线);
(2)如果小亮的身高,测得小亮影长,小亮与灯杆的距离,请求出灯杆的高.
19.如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分落在地面CE上,一部分落在墙EF上.
(1)请你在墙上画出表示CD的部分影子EH;
(2)若量得CE=1.2米,EH=1.5米,求立柱CD的高.
20.如图,在阳光下,身高165cm的小军测得自己的影长为0.9m,同时还测得教学楼的影长为8.1m,求该教学楼的高度.
参考答案
1.A
2.B
3.A
4.D
5.A
6.B
7.B
8.C
9.D
10.B
11.正确
12.1.9
13.8
14.
15.4
16.8
17.(1)见解析;(2)12m
【详解】
(1)如图;
(2)由题意可知:△ABC∽△DGE
∴,即
解得,
所以旗杆的长为12.
18.(1)见解析;(2)12m.
【详解】
(1)根据中心投影的基本规律,画图如下:
(2)由题意可知
∴,
∴,
∴m.
19.(1)作图见解析;(2)2.5米
【详解】
(1)如图,线段EH为所求;
(2)过点E作EM//BG,交CD于点M,
则四边形DHEM是平行四边形,△ABG∽△CME,
即DM=EH=1.5,
∵,
∴
∴
∴(米),
故立柱CD的高为2.5米.
20.14.85m
【详解】
解:设教学楼的高度为xm,根据题意得:
,
解得:x=14.85,
答:教学楼的高度为14.85m.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.在小明住的小区有一条笔直的路,路中间有一盏路灯,一天晚上他行走在这条路上如图,当他从点走到点的过程,他在灯光照射下的影长与所走路程的变化关系图象大致是( )
A. B. C. D.
2.如图,晚上小明在路灯下沿路从处径直走到处,这一过程中他在地上的影子( )
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
3.在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下( )
A.不能够确定谁的影子长 B.小刚的影子比小红的影子短
C.小刚跟小红的影子一样长 D.小刚的影子比小红的影子长
4.如图,在平面直角坐标系中,点是一个光源.木杆AB两端的坐标分别为,.则木杆AB在x轴上的投影长为( ).
A.4 B.5 C.6 D.8
5.如图,从点观测建筑物的视角是( )
A. B. C. D.
6.如图,AB是直立在校园内的一根灯柱,AB的长为6 m,它在阳光下的影子BE的长度为3 m,在同一时刻,灯柱AB旁边的一根旗杆CD在地面上的影子DF的长度为7m,则旗杆CD的高度是( )
A.21 m B.14 m C.7 m D.6 m
7.为了测量操场中旗杄的高度,小明学习了“太阳光与影子”,设计了如图所示的测量方案,根据图中标示的数据可知旗杆的高度为( )
A.4m B.6m C.8m D.9m
8.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3 B.5 C.6 D.7
9.身高米的小明同学利用相似三角形测量学校旗杆的高度,上午点,小明在阳光下的影长为米,此时测得旗杆的影长为米,则学校旗杆的高度是( )
A.米 B.米 C.米 D.米
10.如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
A.逐渐变短 B.先变短后变长
C.先变长后变短 D.逐渐变长
二、填空题
11.晚上行走时,当你离路灯越近时,你的影子就越短.(______)
12.张三和李四并排站立在阳光下,张三身高1.80米,他的影长2.0米,李四比张三矮9厘米,此时李四的影长是___米.
13.如图,一棵树(AB)的高度为7.5米,下午某一个时刻它在水平地面上形成的树影长(BE)为10米,现在小明想要站这棵树下乘凉,他的身高为1.5米,那么他最多可以离开树干多少米才可以不被阳光晒到?____.
14.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成角时,第二次是阳光与地面成角时,两次测量的影长相差8米,则树高______米.(结果保留根号)
15.如图,小明在A时测得旗杆的影长是2米,B时测得旗杆的影长是8米,两次的日照光线恰好互相垂直,则旗杆的高度是______米.
16.在某一时刻,测得一根长为1.5m的标杆的影长为3m,同时测得一根旗杆的影长为16m,那么这根旗杆的高度为_______m.
三、解答题
17.如图,小明与同学合作利用太阳光线测量旗杆的高度,身高的小明()落在地面上的影长.
(1)请画出旗杆在同一时刻阳光照射下在地面上的影子.
(2)若小明测得此刻旗杆落在地面上的影长,求旗杆的高度.
18.晚上,小亮在广场乘凉,图中线段表示站立在广场上的小亮,线段表示直立在广场上的灯杆,点表示照明灯.
(1)请你在图中画出小亮在照明灯照射下的影子(请保留作图痕迹,并把影子描成粗线);
(2)如果小亮的身高,测得小亮影长,小亮与灯杆的距离,请求出灯杆的高.
19.如图,身高1.5米的小明(AB)在太阳光下的影子AG长1.8米,此时,立柱CD的影子一部分落在地面CE上,一部分落在墙EF上.
(1)请你在墙上画出表示CD的部分影子EH;
(2)若量得CE=1.2米,EH=1.5米,求立柱CD的高.
20.如图,在阳光下,身高165cm的小军测得自己的影长为0.9m,同时还测得教学楼的影长为8.1m,求该教学楼的高度.
参考答案
1.A
2.B
3.A
4.D
5.A
6.B
7.B
8.C
9.D
10.B
11.正确
12.1.9
13.8
14.
15.4
16.8
17.(1)见解析;(2)12m
【详解】
(1)如图;
(2)由题意可知:△ABC∽△DGE
∴,即
解得,
所以旗杆的长为12.
18.(1)见解析;(2)12m.
【详解】
(1)根据中心投影的基本规律,画图如下:
(2)由题意可知
∴,
∴,
∴m.
19.(1)作图见解析;(2)2.5米
【详解】
(1)如图,线段EH为所求;
(2)过点E作EM//BG,交CD于点M,
则四边形DHEM是平行四边形,△ABG∽△CME,
即DM=EH=1.5,
∵,
∴
∴
∴(米),
故立柱CD的高为2.5米.
20.14.85m
【详解】
解:设教学楼的高度为xm,根据题意得:
,
解得:x=14.85,
答:教学楼的高度为14.85m.
