32.3直棱柱与圆锥的侧面展开图同步课时训练(Word版 含答案)
文档属性
| 名称 | 32.3直棱柱与圆锥的侧面展开图同步课时训练(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 294.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览

文档简介
32.3直棱柱与圆锥的侧面展开图同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
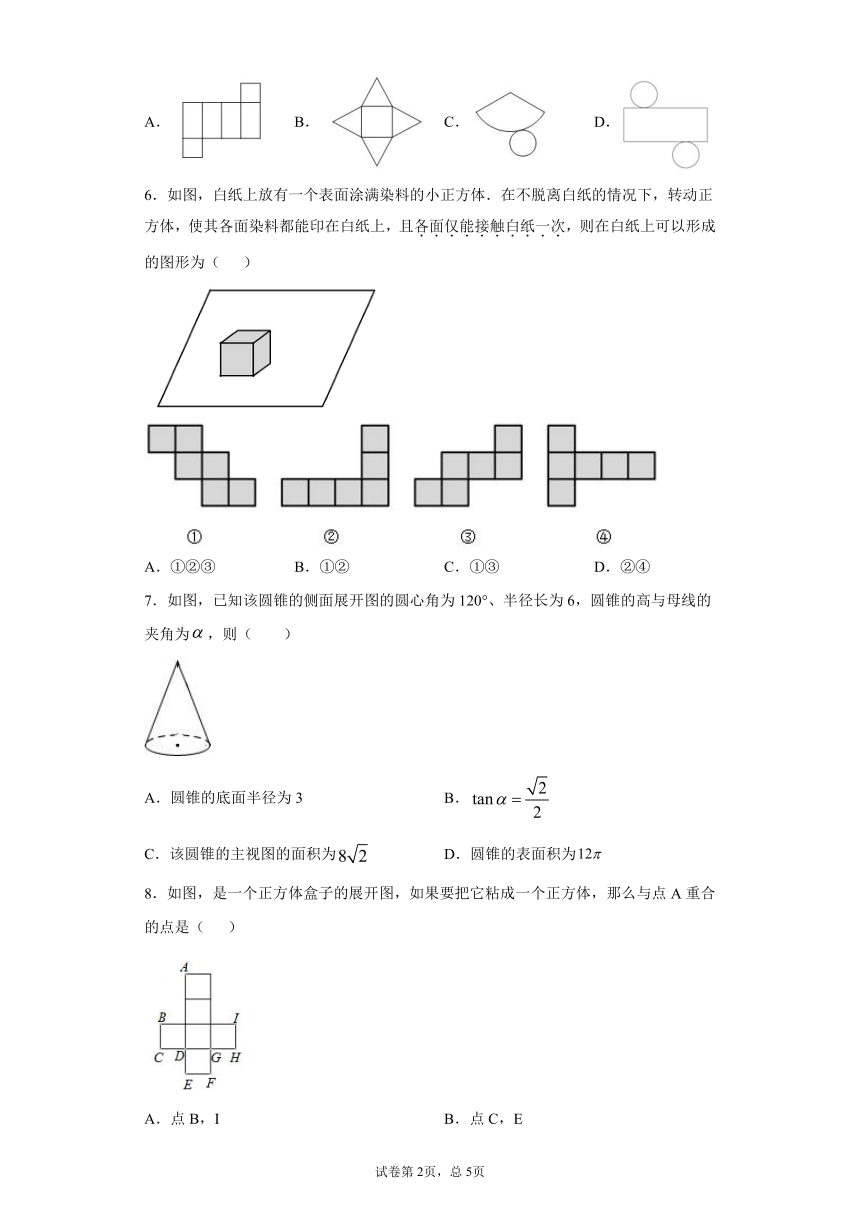
1.下图是正方体的展开图,则原正方体“5”与相对面上的数字之和是( )
A.9 B.8 C.7 D.6
2.下列各图中,经过折叠不能围成一个立方体的是( )
A. B. C. D.
3.写有“全国文明城市”的正方体展开图如图所示,与“全”字相对的字是( )
A.文 B.明 C.城 D.市
4.如图,已知圆锥的母线长为,底面半径为,则此圆锥侧面展开图的圆心角的度数是( )
A. B. C. D.
5.下列几何体的展开图中,能围成圆柱的是( )
A. B. C. D.
6.如图,白纸上放有一个表面涂满染料的小正方体.在不脱离白纸的情况下,转动正方体,使其各面染料都能印在白纸上,且各面仅能接触白纸一次,则在白纸上可以形成的图形为( )
A.①②③ B.①② C.①③ D.②④
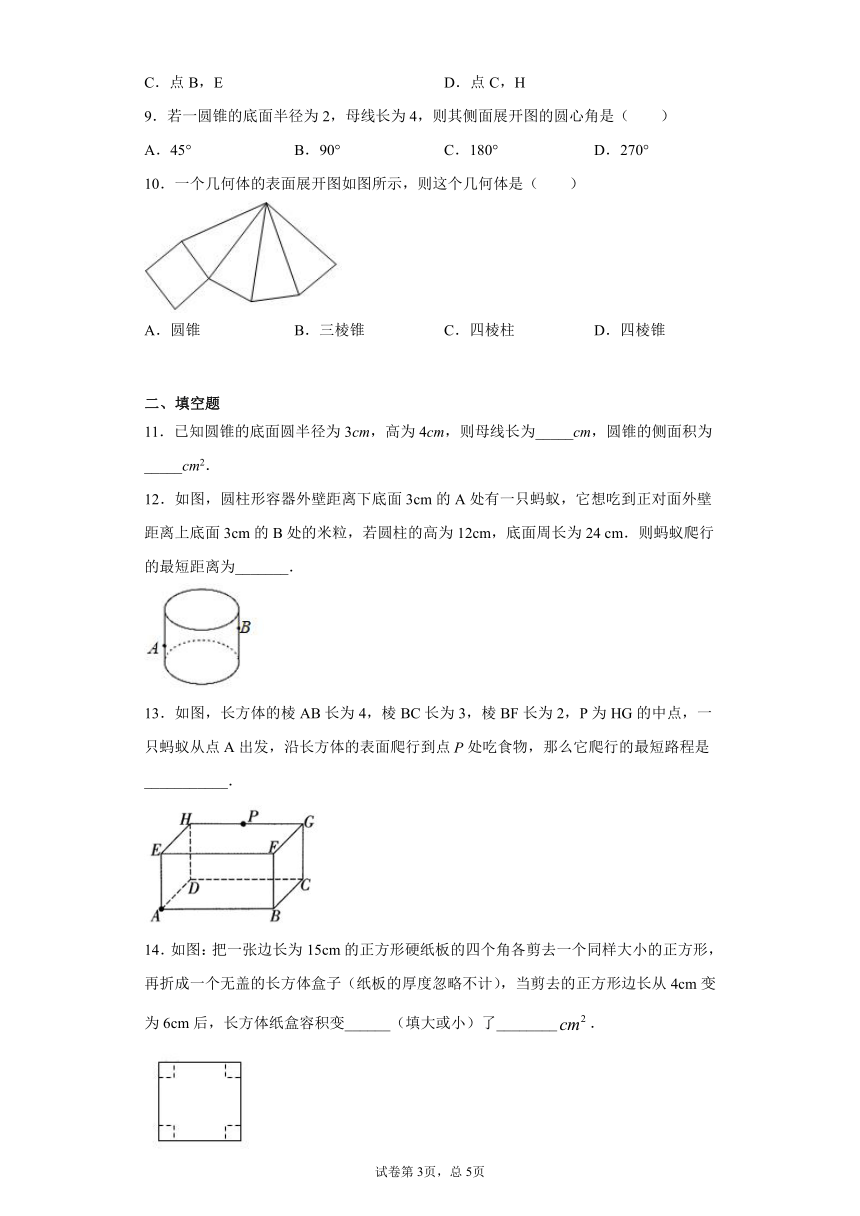
7.如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为,则( )
A.圆锥的底面半径为3 B.
C.该圆锥的主视图的面积为 D.圆锥的表面积为
8.如图,是一个正方体盒子的展开图,如果要把它粘成一个正方体,那么与点A重合的点是( )
A.点B,I B.点C,E
C.点B,E D.点C,H
9.若一圆锥的底面半径为2,母线长为4,则其侧面展开图的圆心角是( )
A.45° B.90° C.180° D.270°
10.一个几何体的表面展开图如图所示,则这个几何体是( )
A.圆锥 B.三棱锥 C.四棱柱 D.四棱锥
二、填空题
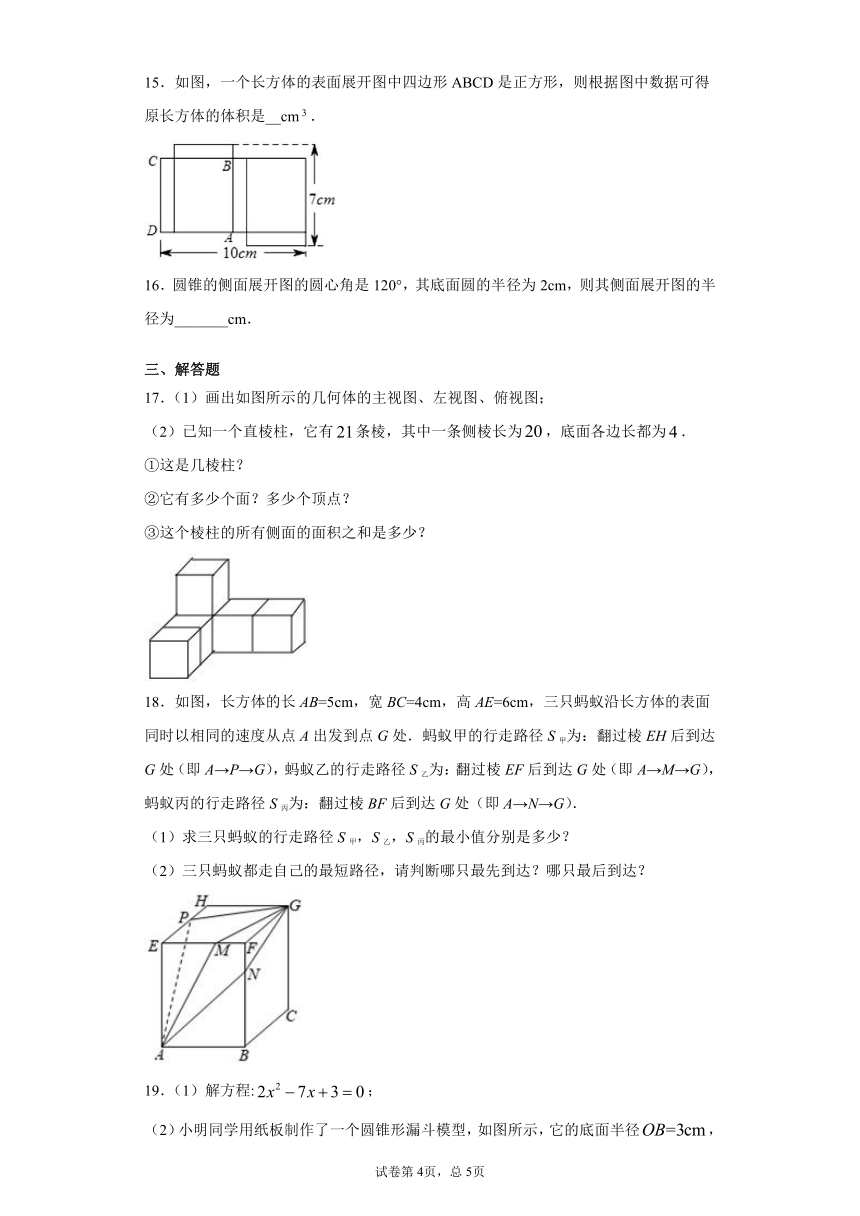
11.已知圆锥的底面圆半径为3cm,高为4cm,则母线长为_____cm,圆锥的侧面积为_____cm2.
12.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B处的米粒,若圆柱的高为12cm,底面周长为24 cm.则蚂蚁爬行的最短距离为_______.
13.如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点处吃食物,那么它爬行的最短路程是___________.
14.如图:把一张边长为15cm的正方形硬纸板的四个角各剪去一个同样大小的正方形,再折成一个无盖的长方体盒子(纸板的厚度忽略不计),当剪去的正方形边长从4cm变为6cm后,长方体纸盒容积变______(填大或小)了________.
15.如图,一个长方体的表面展开图中四边形ABCD是正方形,则根据图中数据可得原长方体的体积是__cm.
16.圆锥的侧面展开图的圆心角是120°,其底面圆的半径为2cm,则其侧面展开图的半径为_______cm.
三、解答题
17.(1)画出如图所示的几何体的主视图、左视图、俯视图;
(2)已知一个直棱柱,它有条棱,其中一条侧棱长为,底面各边长都为.
①这是几棱柱?
②它有多少个面?多少个顶点?
③这个棱柱的所有侧面的面积之和是多少?
18.如图,长方体的长AB=5cm,宽BC=4cm,高AE=6cm,三只蚂蚁沿长方体的表面同时以相同的速度从点A出发到点G处.蚂蚁甲的行走路径S甲为:翻过棱EH后到达G处(即A→P→G),蚂蚁乙的行走路径S乙为:翻过棱EF后到达G处(即A→M→G),蚂蚁丙的行走路径S丙为:翻过棱BF后到达G处(即A→N→G).
(1)求三只蚂蚁的行走路径S甲,S乙,S丙的最小值分别是多少?
(2)三只蚂蚁都走自己的最短路径,请判断哪只最先到达?哪只最后到达?
19.(1)解方程:;
(2)小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径,高,求这个圆锥形漏斗的侧面展开图的圆心角的度数.
20.如图1所示,从大正方体中截去一个小正方体之后,可以得到图2的几何体.
(1)设原大正方体的表面积为a,图2中几何体的表面积为b,那么a与b的大小关系是 ;
A.a>b;B.a<b;C.a=b;D.无法判断.
(2)小明说“设图1中大正方体的棱长之和为m,图2中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图3是图2几何体的表面展开图吗?如有错误,请予修正.
参考答案
1.D
2.C
3.B
4.C
5.D
6.C
7.C
8.B
9.C
10.D
11.5 15π
12.
13.5
14.小 142
15.20
16.6cm
17.(1)见解析;(2)①七棱柱;②它有个面,个顶点;③侧面积之和为.
【详解】
解:(1)根据几何体的主视图、左视图、俯视图的画法画出图形如下:
(2)①一个直棱柱有条棱,
这个直棱柱是七棱柱,
②七棱柱有个面,个顶点,
③七棱柱有个侧面,都是长为,宽为的长方形,
所以,
答:这个直棱柱是七棱柱,它有个面,个顶点,侧面积之和为.
18.(1)三只蚂蚁的行走路径S甲,S乙,S丙的最小值分别是cm,5cm,cm;(2)蚂蚁丙最先到达,蚂蚁甲最后到达
【详解】
解:(1)将长方体侧面展开,由行走路径最小值确定:路线为线段,
∵长AB=5cm,宽BC=4cm,高AE=6cm,
∴EF=AB=5cm,GF=BC=EH=4cm,AE=BF=CG=6cm,
∴图1:S甲=(cm)
图2:S乙=(cm),
图3:S丙=(cm),
答:三只蚂蚁的行走路径S甲,S乙,S丙的最小值分别是cm,5cm,cm;
(2)由(1)知,S甲=(cm),S乙=5=(cm),S丙=(cm).
∵>>,
∴蚂蚁丙最先到达,蚂蚁甲最后到达.
19.(1);(2)这个圆锥形漏斗的侧面展开图的圆心角的度数为216°
【详解】
解:(1)
a=2,b=-7,c=3
∴x=
解得:;
(2)该圆锥侧面展开图的半径BC=
侧面展开图的弧长即为底面圆的周长为cm
∴侧面展开图的圆心角的度数为
答:这个圆锥形漏斗的侧面展开图的圆心角的度数为216°.
20.(1)C;(2)不正确,理由见解析;(3)图③不是图②几何体的表面展开图,改后的图形见解析
【详解】
解:(1)根据“切去三个小面”但又“新增三个相同的小面”,因此与原来的表面积相等,即a=b
故答案为:a=b;
(2)如图④红颜色的棱是多出来的,共6条,当且仅当每一条棱都等于原来正方体的棱长的一半,n比m正好多出大正方体的3条棱的长度,故小明的说法是不正确的;
图④ 图⑤
(3)图③不是图②几何体的表面展开图,改后的图形,如图⑤所示.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下图是正方体的展开图,则原正方体“5”与相对面上的数字之和是( )
A.9 B.8 C.7 D.6
2.下列各图中,经过折叠不能围成一个立方体的是( )
A. B. C. D.
3.写有“全国文明城市”的正方体展开图如图所示,与“全”字相对的字是( )
A.文 B.明 C.城 D.市
4.如图,已知圆锥的母线长为,底面半径为,则此圆锥侧面展开图的圆心角的度数是( )
A. B. C. D.
5.下列几何体的展开图中,能围成圆柱的是( )
A. B. C. D.
6.如图,白纸上放有一个表面涂满染料的小正方体.在不脱离白纸的情况下,转动正方体,使其各面染料都能印在白纸上,且各面仅能接触白纸一次,则在白纸上可以形成的图形为( )
A.①②③ B.①② C.①③ D.②④
7.如图,已知该圆锥的侧面展开图的圆心角为120°、半径长为6,圆锥的高与母线的夹角为,则( )
A.圆锥的底面半径为3 B.
C.该圆锥的主视图的面积为 D.圆锥的表面积为
8.如图,是一个正方体盒子的展开图,如果要把它粘成一个正方体,那么与点A重合的点是( )
A.点B,I B.点C,E
C.点B,E D.点C,H
9.若一圆锥的底面半径为2,母线长为4,则其侧面展开图的圆心角是( )
A.45° B.90° C.180° D.270°
10.一个几何体的表面展开图如图所示,则这个几何体是( )
A.圆锥 B.三棱锥 C.四棱柱 D.四棱锥
二、填空题
11.已知圆锥的底面圆半径为3cm,高为4cm,则母线长为_____cm,圆锥的侧面积为_____cm2.
12.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B处的米粒,若圆柱的高为12cm,底面周长为24 cm.则蚂蚁爬行的最短距离为_______.
13.如图,长方体的棱AB长为4,棱BC长为3,棱BF长为2,P为HG的中点,一只蚂蚁从点A出发,沿长方体的表面爬行到点处吃食物,那么它爬行的最短路程是___________.
14.如图:把一张边长为15cm的正方形硬纸板的四个角各剪去一个同样大小的正方形,再折成一个无盖的长方体盒子(纸板的厚度忽略不计),当剪去的正方形边长从4cm变为6cm后,长方体纸盒容积变______(填大或小)了________.
15.如图,一个长方体的表面展开图中四边形ABCD是正方形,则根据图中数据可得原长方体的体积是__cm.
16.圆锥的侧面展开图的圆心角是120°,其底面圆的半径为2cm,则其侧面展开图的半径为_______cm.
三、解答题
17.(1)画出如图所示的几何体的主视图、左视图、俯视图;
(2)已知一个直棱柱,它有条棱,其中一条侧棱长为,底面各边长都为.
①这是几棱柱?
②它有多少个面?多少个顶点?
③这个棱柱的所有侧面的面积之和是多少?
18.如图,长方体的长AB=5cm,宽BC=4cm,高AE=6cm,三只蚂蚁沿长方体的表面同时以相同的速度从点A出发到点G处.蚂蚁甲的行走路径S甲为:翻过棱EH后到达G处(即A→P→G),蚂蚁乙的行走路径S乙为:翻过棱EF后到达G处(即A→M→G),蚂蚁丙的行走路径S丙为:翻过棱BF后到达G处(即A→N→G).
(1)求三只蚂蚁的行走路径S甲,S乙,S丙的最小值分别是多少?
(2)三只蚂蚁都走自己的最短路径,请判断哪只最先到达?哪只最后到达?
19.(1)解方程:;
(2)小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径,高,求这个圆锥形漏斗的侧面展开图的圆心角的度数.
20.如图1所示,从大正方体中截去一个小正方体之后,可以得到图2的几何体.
(1)设原大正方体的表面积为a,图2中几何体的表面积为b,那么a与b的大小关系是 ;
A.a>b;B.a<b;C.a=b;D.无法判断.
(2)小明说“设图1中大正方体的棱长之和为m,图2中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图3是图2几何体的表面展开图吗?如有错误,请予修正.
参考答案
1.D
2.C
3.B
4.C
5.D
6.C
7.C
8.B
9.C
10.D
11.5 15π
12.
13.5
14.小 142
15.20
16.6cm
17.(1)见解析;(2)①七棱柱;②它有个面,个顶点;③侧面积之和为.
【详解】
解:(1)根据几何体的主视图、左视图、俯视图的画法画出图形如下:
(2)①一个直棱柱有条棱,
这个直棱柱是七棱柱,
②七棱柱有个面,个顶点,
③七棱柱有个侧面,都是长为,宽为的长方形,
所以,
答:这个直棱柱是七棱柱,它有个面,个顶点,侧面积之和为.
18.(1)三只蚂蚁的行走路径S甲,S乙,S丙的最小值分别是cm,5cm,cm;(2)蚂蚁丙最先到达,蚂蚁甲最后到达
【详解】
解:(1)将长方体侧面展开,由行走路径最小值确定:路线为线段,
∵长AB=5cm,宽BC=4cm,高AE=6cm,
∴EF=AB=5cm,GF=BC=EH=4cm,AE=BF=CG=6cm,
∴图1:S甲=(cm)
图2:S乙=(cm),
图3:S丙=(cm),
答:三只蚂蚁的行走路径S甲,S乙,S丙的最小值分别是cm,5cm,cm;
(2)由(1)知,S甲=(cm),S乙=5=(cm),S丙=(cm).
∵>>,
∴蚂蚁丙最先到达,蚂蚁甲最后到达.
19.(1);(2)这个圆锥形漏斗的侧面展开图的圆心角的度数为216°
【详解】
解:(1)
a=2,b=-7,c=3
∴x=
解得:;
(2)该圆锥侧面展开图的半径BC=
侧面展开图的弧长即为底面圆的周长为cm
∴侧面展开图的圆心角的度数为
答:这个圆锥形漏斗的侧面展开图的圆心角的度数为216°.
20.(1)C;(2)不正确,理由见解析;(3)图③不是图②几何体的表面展开图,改后的图形见解析
【详解】
解:(1)根据“切去三个小面”但又“新增三个相同的小面”,因此与原来的表面积相等,即a=b
故答案为:a=b;
(2)如图④红颜色的棱是多出来的,共6条,当且仅当每一条棱都等于原来正方体的棱长的一半,n比m正好多出大正方体的3条棱的长度,故小明的说法是不正确的;
图④ 图⑤
(3)图③不是图②几何体的表面展开图,改后的图形,如图⑤所示.
