苏科版八年级下册 第11章 反比例函数 --知识点及典型例题 提优训练 讲义(word版无答案)
文档属性
| 名称 | 苏科版八年级下册 第11章 反比例函数 --知识点及典型例题 提优训练 讲义(word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 04:28:32 | ||
图片预览




文档简介
反比例函数专题
细心
多思
勤练
反比例函数复习
一、本章知识网络图
二、知识点及考点:
(一)反比例函数的概念:
知识要点:
1、一般地,形如
y
=
(
k是常数,
k
≠
0
)
的函数叫做反比例函数。
注意:(1)常数
k
称为比例系数,k
是非零常数;
(2)解析式有三种常见的表达形式:
(A)y
=
(k
≠
0)
,
(B)xy
=
k(k
≠
0)
(C)y=kx-1(k≠0)
例题讲解:
有关反比例函数的解析式
(1)下列函数,①
②.
③
④.⑤⑥
;其中是y关于x的反比例函数的有:_________________。
(2)函数是反比例函数,则k的值是( )
A.-1
B.-2
C.2
D.2或-2
(3)若函数(m是常数)是反比例函数,则m=________,解析式为________.
(4)如果是的反比例函数,是的反比例函数,那么是的(
)
A.反比例函数
B.正比例函数
C.一次函数
D.反比例或正比例函数
练习:(1)如果是的正比例函数,是的反比例函数,那么是的(
)
(2)如果是的正比例函数,是的正比例函数,那么是的(
)
(5)反比例函数的图象经过(—2,5)和(,
),
求1)的值;
2)判断点B(,)是否在这个函数图象上,并说明理由
(6)已知y与2x-3成反比例,且时,y=-2,求y与x的函数关系式.
(7)已知函数,其中与成正比例,
与成反比例,且当=1时,=1;
=3时,=5.求:(1)求关于的函数解析式; (2)当=2时,的值.
(二)反比例函数的图象和性质:
知识要点:
1、形状:图象是双曲线。
2、位置:(1)当k>0时,双曲线分别位于第________象限内;(2)当k<0时,
双曲线分别位于第________象限内。
3、增减性:(1)当k>0时,_________________,y随x的增大而________;
(2)当k<0时,_________________,y随x的增大而______。
4、变化趋势:双曲线无限接近于x、y轴,但永远不会与坐标轴相交
5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点____________;(2)对于k取互为相反数的两个反比例函数(如:y
=
和y
=
)来说,它们是关于x轴,y轴___________。
例题讲解:
反比例函数的图象和性质:
(1)写出一个反比例函数,使它的图象经过第二、四象限 .
(2)若反比例函数的图象在第二、四象限,则的值是(
)
A、
-1或1;
B、小于的任意实数;
C、-1;
D、不能确定
(3)下列函数中,当时,随的增大而增大的是( )
A. B. C. D..
(4)已知反比例函数的图象上有两点A(,),B(,),且,
则的值是(
)
A.正数
B.负数
C.非正数 D.不能确定
(5)若点(,)、(,)和(,)分别在反比例函数
的图象上,且
,则下列判断中正确的是( )
A. B. C. D.
(6)在反比例函数的图象上有两点和,若时,,则的取值范围是 .
(7)老师给出一个函数,甲、乙、丙三位同学分别指出了这个函数的一个性质:
甲:函数的图象经过第二象限;
乙:函数的图象经过第四象限;
丙:在每个象限内,y随x的增大而增大.
请你根据他们的叙述构造满足上述性质的一个函数:
.
(8)作出反比例函数的图象,结合图象回答:
(1)当x=2时,y的值;
(2)当1<x≤4时,y的取值范围;
(3)当1≤y<4时,x的取值范围.
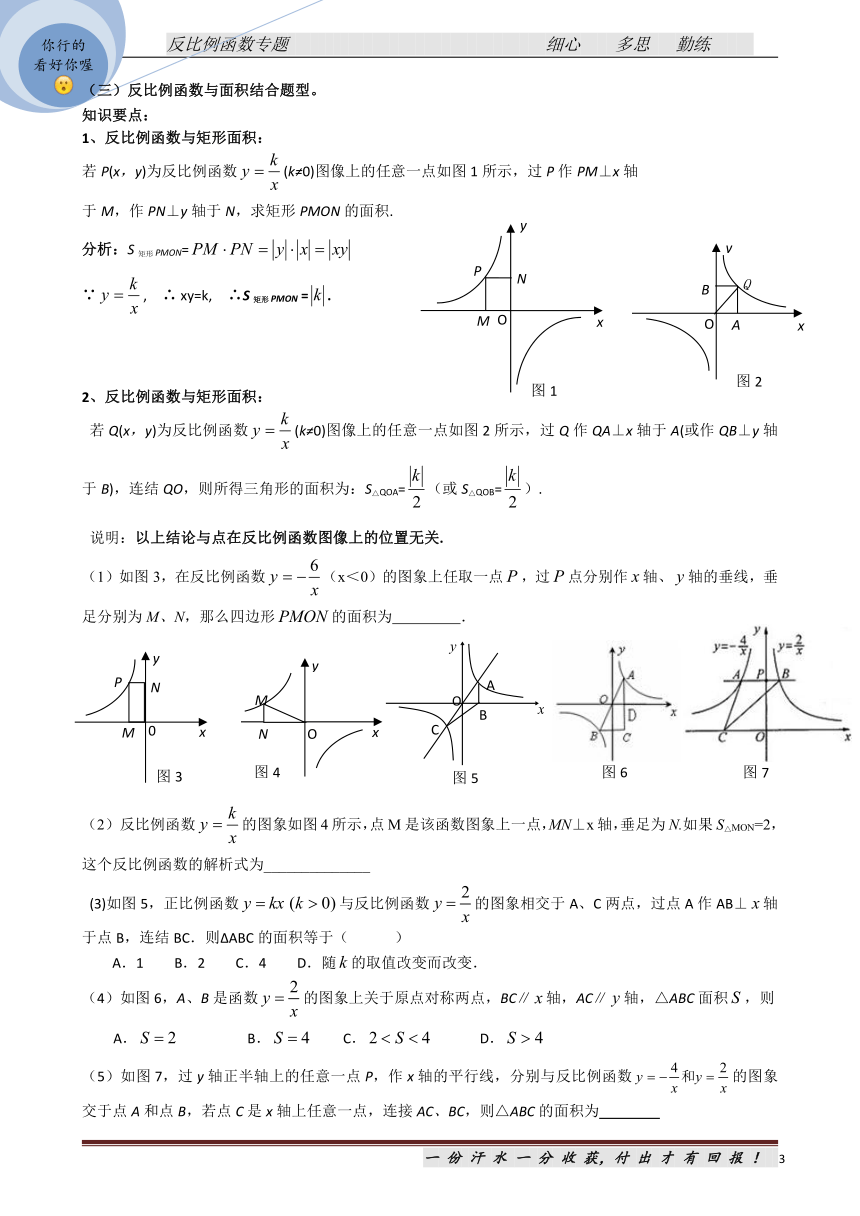
(三)反比例函数与面积结合题型。
知识要点:
1、反比例函数与矩形面积:
若P(x,y)为反比例函数(k≠0)图像上的任意一点如图1所示,过P作PM⊥x轴
于M,作PN⊥y轴于N,求矩形PMON的面积.
分析:S矩形PMON=
∵,
∴
xy=k,
∴S矩形PMON
=.
2、反比例函数与矩形面积:
若Q(x,y)为反比例函数(k≠0)图像上的任意一点如图2所示,过Q作QA⊥x轴于A(或作QB⊥y轴于B),连结QO,则所得三角形的面积为:S△QOA=(或S△QOB=).
说明:以上结论与点在反比例函数图像上的位置无关.
(1)如图3,在反比例函数(x<0)的图象上任取一点,过点分别作轴、轴的垂线,垂足分别为M、N,那么四边形的面积为
.
(2)
反比例函数的图象如图4所示,点M是该函数图象上一点,MN⊥x轴,垂足为N.如果S△MON=2,这个反比例函数的解析式为______________
(3)如图5,正比例函数与反比例函数的图象相交于A、C两点,过点A作AB⊥轴于点B,连结BC.则ΔABC的面积等于( )
A.1 B.2 C.4 D.随的取值改变而改变.
(4)如图6,A、B是函数的图象上关于原点对称两点,BC∥轴,AC∥轴,△ABC面积,则
A.
B. C. D.
(5)如图7,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为
(四)一次函数与反比例函数
(1)一次函数y=﹣2x+1和反比例函数y=的大致图象是( )
A、
B、
C、
D、
(2)一次函数和反比例函数在同一直角坐标系中的图象大致是(
)
(3)一次函数y1=
k1x
+b和反比例函数y2
=(k1?k2≠0)的图象如图所示,若y1>y2,
则x的取值范围是( )
A、﹣2<x<0或x>1
B、﹣2<x<1
C、x<﹣2或x>1
D、x<﹣2或0<x<1
(4)正比例函数和反比例函数的图象有
个交点.
(5)正比例函数y=k1x(k1≠0)和反比例函数y=
(k2≠0)的一个交点为(m,n),则另一个交点为_________.
(6)设函数y=与y=x﹣1的图象的交点坐标为(a,b),则
QUOTE
的值为
(7)如图,RtΔABO的顶点A是双曲线与直线在第二象限的交点,
AB垂直轴于B,且S△ABO=,则反比例函数的解析式 .
(8)若反比例函数与一次函数y=3x+b都经过点(1,4),则kb=________.
(9)如图,已知A
(4,a),B
(-2,-4)是一次函数y=kx+b图象和反比例函数y=-
图象的交点.(1)求反比例函数和一次函数的解祈式;(2)求△A0B的面积.
(10)如图,在平面直角坐标系中,直线与双曲线在第一象限交于点A,与轴交于点C,AB⊥轴,垂足为B,且=1.求:(1)求两个函数解析式; (2)求△ABC的面积.
(11)平面直角坐标系中,直线AB交x轴于点A,交y轴于点B
且与反比例函数图象分别交于C、D两点,过点C作CM⊥x轴于M,AO=6,BO=3,CM=5.求直线AB的解析式和反比例函数解析式.
(五)反比例函数的应用:
例题讲解:
1.一个水池装水12立方米,如果从水管中每小时流出x立方米的水,经过y小时可以把水放完,那么y与x的函数关系式是________,自变量x的取值范围是________.
2.三角形的面积为6cm2,如果它的一边为ycm,这边上的高为xcm,那么y与x之间是________函数关系,以x为自变量的函数解析式为________.
3.长方体的体积为40cm3,此长方体的底面积y(cm2)与其对应高x(cm)之间的函数关系用图象大致可以表示为下面的(
).
4.下列各问题中两个变量之间的关系,不是反比例函数的是(
).
(A)小明完成百米赛跑时,所用时间t(s)与他的平均速度v(m/s)之间的关系
(B)长方形的面积为24,它的长y与宽x之间的关系
(C)压力为600N时,压强p(Pa)与受力面积S(m2)之间的关系
(D)一个容积为25L的容器中,所盛水的质量m(kg)与所盛水的体积V(L)之间的关系
5.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:
体积x(ml)
100
80
60
40
20
压强y(kpa)
60
75
100
150
300
则可以反映y与x之间的关系的式子是(
).
(A)y=3000x
(B)y=6000x
(C)
(D)
6.甲、乙两地间的公路长为300km,一辆汽车从甲地去乙地,汽车在途中的平均速度为V(km/h),到达时所用的时间为t(h),那么t是V________的函数,V关于t的函数关系式为________.
7.农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房(如图所示),则需要
塑料布y(m2)与半径R(m)的函数关系式是(不考虑塑料埋在土里的部分)________.
8.有一面积为60的梯形,其上底是下底长的三分之一,若下底长为x,高为y,
则y关于x的函数关系式是(
).
(A)
(B)
(C)
(D)
9.一个气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)写出这一函数的解析式;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kPa时,气球将爆炸,为了安全
起见,气体的体积应不小于多少?
10.某学校对教室采用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题图中所提供的信息解答下列问题:
(1)药物燃烧时y关于x的函数关系式为________,自变量x的取值范围是________;药物燃烧后y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量小于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过________分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
《反比例函数》巩固练习
一、选择题(本大题共10小题,每小题3分,共30分)
1.如果反比例函数的图象经过点,那么它还一定经过(
)
A.
B.
C.
D.
2.如图1,在平面直角坐标系中,点是轴正半轴上的一个定点,点是双曲线
上的一个动点,当点的横坐标逐渐增大时,的面积将(
)
A.逐渐增大
B.不变
C.逐渐减小
D.先增大,后减小
3.如果反比例函数的图象与直线没有交点,那么符合条件的值为(
)
A.
B.
C.
D.
4.在反比例函数的图象上有两个点,且,,则的取值范围是(
)
A.
B.
C.
D.
5.如图2,反比例函数与正比例函数的图象的一个交点坐标是,若,则的取值范围在数轴上表示为(
)
6.如图3,点是反比例函数图象上一点,过点作轴的平行线,交反比例函数的图象于点,连接,若的面积为2,则的值为(
)
A.
B.
C.
D.
7.设的一边长为,这条边上的高为,与满足的反比例函数关系如图4
所示,当为等腰直角三角形时,的值为(
)
A.
B.
C.
或
D.
或
8.在数学活动课上,小华借助下列表格中的数据,在平面直角坐标系中经历描点和连线
的步骤,正确绘制了某个反比例函数的图象,则下列关于该函数的描述错误的是(
)
A.图象在第二、四象限
B.图象必经过点
C.图象与坐标轴没有交点
D.当时,的取值范围是
9.如图5,点在反比例函数的图象上,且横坐标为2.若将点先向右平移两个单位,再向上平移一个单位后得到点,则在第一象限内,经过点的反比例函数图象的表达式是(
)
A.
B.
C.
D.
10.如图6,和的各顶点分别在双曲线,,的第一象限的图象上,,轴,轴,则(
)
A.
B.
C.
D.
二、填空题(本大题共10小题,每小题3分,共30分)
11.若梯形的下底长为,上底长为下底长的,高为,面积为60,则与的函数关系式是
(不考虑的取值范围).
12.如果关于的函数是反比例函数,那么的值等于
.
13.如图7,点是双曲线上的点,分别经过两点向轴、轴作垂线段,若,则
.
14.若反比例函数的函数图象过点,则与的大小关系是
.(填“>”或“=”“<”)
15.如图8,一次函数的图象与反比例函数的图象相交于两点,当时,,或,则一次函数的表达式为
.
16.在平面直角坐标系中,点的坐标为,点的坐标为,四边形为矩形,点为线段上的一个动点,若为等腰三角形,且点在双曲线上,则的值可以是
.
17.
如图9,已知双曲线,点为双曲线上的一点,且轴于点,轴于点,分别交双曲线于两点,
则的面积是
.
18.直线,与双曲线交于两点,
则
.
19.我们已经学习过反比例函数的图象和性质,请回顾研究它的过程,对函数进行探索,下列结论:
①图象在第一、二象限;
②图象在第一、三象限;
③图象关于轴对称;
④图象关于原点对称;
⑤当时,随增大而增大;当时,随增大而增大;
⑥当时,随增大而减小;当时,随增大而增大.
其中是函数的性质及它的图象特征的是
.(填写所有正确答案的序号)
20.如图10,在x轴的正半轴上依次截取,过点,分别作轴的垂线与反比例函数的图象相交于点,得直角三角形,,,,,并设其面积分别为,则的值为
,以此类推
(的整数).
三、解答题(本大题共6小题,共60分)
21.
(
8分)已知变量与成反比例函数,并且当时,.
(1)求与之间的函数关系式.
(2)求时,的值.
22.(10分)函数的图象如图11所示.
(1)在同一平面直角坐标系中,用描点法画下列函数的图象.
①;②.
列表:
画图象,并注明函数表达式.
(2)观察图象,完成填空:
①将函数的图象向
平移
个单位,可得函数的图象;
②将函数的图象向
平移
个单位,可得函数的图象.
(3)函数的图象经过怎样的变化,可得函数的图象?(写出一种即可)
23.
(
8分)如图12,已知一次函数(为常数)的图象与反比例函数(为常数,)的图象相交于点.
(1)求这两个函数的表达式及其图象的另一个交点的坐标.
(2)观察图象,写出使函数值的自变量的取值范围.
24.
(10分)如图13,在平面直角坐标系中,直线与双曲线相交于点和点.
(1)求直线与双曲线的表达式.
(2)对于横、纵坐标都是整数的点叫做整点.动点是双曲线上的整点,过点作垂直于轴的直线,交直线于点,当点位于点的下方时,请直接写出整点的坐标.
25.
(12分)一辆汽车匀速通过某段公路,所需时间(h)与行驶速度(km/h)满足函数关系式,其图象为如图14所示的一段曲线且端点为和.
(1)求和的值.
(2)若行驶速度不得超过60km/h,则汽车通过该路段最少需要多少时间?
26.
(12分)“保护生态环境,建设绿色社会”已经从理念变为人们的行动.某化工厂2017年1月的利润为200万元.设2017年1月为第1个月,第个月的利润为万元.由于排污超标,该厂决定从2017年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,与成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图15
).
(1)分别求该化工厂治污期间及治污改造工程完工后,与之间对应的函数关系式.
(2)治污改造工程完工后经过几个月,该厂月利润才能达到2017年1月的水平?
(3)当月利润少于100万元时,为该厂资金紧张期,问该厂资金紧张期共有几个月?
反
比例
函
数
P
y
x
O
M
N
图1
O
B
y
x
A
Q
图2
图6
O
A
C
B
M
y
N
x
O
图4
P
y
M
x
0
N
图3
图5
图7
(第(7)题)
一
份
汗
水
一
分
收
获,付
出
才
有
回
报
!
1
细心
多思
勤练
反比例函数复习
一、本章知识网络图
二、知识点及考点:
(一)反比例函数的概念:
知识要点:
1、一般地,形如
y
=
(
k是常数,
k
≠
0
)
的函数叫做反比例函数。
注意:(1)常数
k
称为比例系数,k
是非零常数;
(2)解析式有三种常见的表达形式:
(A)y
=
(k
≠
0)
,
(B)xy
=
k(k
≠
0)
(C)y=kx-1(k≠0)
例题讲解:
有关反比例函数的解析式
(1)下列函数,①
②.
③
④.⑤⑥
;其中是y关于x的反比例函数的有:_________________。
(2)函数是反比例函数,则k的值是( )
A.-1
B.-2
C.2
D.2或-2
(3)若函数(m是常数)是反比例函数,则m=________,解析式为________.
(4)如果是的反比例函数,是的反比例函数,那么是的(
)
A.反比例函数
B.正比例函数
C.一次函数
D.反比例或正比例函数
练习:(1)如果是的正比例函数,是的反比例函数,那么是的(
)
(2)如果是的正比例函数,是的正比例函数,那么是的(
)
(5)反比例函数的图象经过(—2,5)和(,
),
求1)的值;
2)判断点B(,)是否在这个函数图象上,并说明理由
(6)已知y与2x-3成反比例,且时,y=-2,求y与x的函数关系式.
(7)已知函数,其中与成正比例,
与成反比例,且当=1时,=1;
=3时,=5.求:(1)求关于的函数解析式; (2)当=2时,的值.
(二)反比例函数的图象和性质:
知识要点:
1、形状:图象是双曲线。
2、位置:(1)当k>0时,双曲线分别位于第________象限内;(2)当k<0时,
双曲线分别位于第________象限内。
3、增减性:(1)当k>0时,_________________,y随x的增大而________;
(2)当k<0时,_________________,y随x的增大而______。
4、变化趋势:双曲线无限接近于x、y轴,但永远不会与坐标轴相交
5、对称性:(1)对于双曲线本身来说,它的两个分支关于直角坐标系原点____________;(2)对于k取互为相反数的两个反比例函数(如:y
=
和y
=
)来说,它们是关于x轴,y轴___________。
例题讲解:
反比例函数的图象和性质:
(1)写出一个反比例函数,使它的图象经过第二、四象限 .
(2)若反比例函数的图象在第二、四象限,则的值是(
)
A、
-1或1;
B、小于的任意实数;
C、-1;
D、不能确定
(3)下列函数中,当时,随的增大而增大的是( )
A. B. C. D..
(4)已知反比例函数的图象上有两点A(,),B(,),且,
则的值是(
)
A.正数
B.负数
C.非正数 D.不能确定
(5)若点(,)、(,)和(,)分别在反比例函数
的图象上,且
,则下列判断中正确的是( )
A. B. C. D.
(6)在反比例函数的图象上有两点和,若时,,则的取值范围是 .
(7)老师给出一个函数,甲、乙、丙三位同学分别指出了这个函数的一个性质:
甲:函数的图象经过第二象限;
乙:函数的图象经过第四象限;
丙:在每个象限内,y随x的增大而增大.
请你根据他们的叙述构造满足上述性质的一个函数:
.
(8)作出反比例函数的图象,结合图象回答:
(1)当x=2时,y的值;
(2)当1<x≤4时,y的取值范围;
(3)当1≤y<4时,x的取值范围.
(三)反比例函数与面积结合题型。
知识要点:
1、反比例函数与矩形面积:
若P(x,y)为反比例函数(k≠0)图像上的任意一点如图1所示,过P作PM⊥x轴
于M,作PN⊥y轴于N,求矩形PMON的面积.
分析:S矩形PMON=
∵,
∴
xy=k,
∴S矩形PMON
=.
2、反比例函数与矩形面积:
若Q(x,y)为反比例函数(k≠0)图像上的任意一点如图2所示,过Q作QA⊥x轴于A(或作QB⊥y轴于B),连结QO,则所得三角形的面积为:S△QOA=(或S△QOB=).
说明:以上结论与点在反比例函数图像上的位置无关.
(1)如图3,在反比例函数(x<0)的图象上任取一点,过点分别作轴、轴的垂线,垂足分别为M、N,那么四边形的面积为
.
(2)
反比例函数的图象如图4所示,点M是该函数图象上一点,MN⊥x轴,垂足为N.如果S△MON=2,这个反比例函数的解析式为______________
(3)如图5,正比例函数与反比例函数的图象相交于A、C两点,过点A作AB⊥轴于点B,连结BC.则ΔABC的面积等于( )
A.1 B.2 C.4 D.随的取值改变而改变.
(4)如图6,A、B是函数的图象上关于原点对称两点,BC∥轴,AC∥轴,△ABC面积,则
A.
B. C. D.
(5)如图7,过y轴正半轴上的任意一点P,作x轴的平行线,分别与反比例函数的图象交于点A和点B,若点C是x轴上任意一点,连接AC、BC,则△ABC的面积为
(四)一次函数与反比例函数
(1)一次函数y=﹣2x+1和反比例函数y=的大致图象是( )
A、
B、
C、
D、
(2)一次函数和反比例函数在同一直角坐标系中的图象大致是(
)
(3)一次函数y1=
k1x
+b和反比例函数y2
=(k1?k2≠0)的图象如图所示,若y1>y2,
则x的取值范围是( )
A、﹣2<x<0或x>1
B、﹣2<x<1
C、x<﹣2或x>1
D、x<﹣2或0<x<1
(4)正比例函数和反比例函数的图象有
个交点.
(5)正比例函数y=k1x(k1≠0)和反比例函数y=
(k2≠0)的一个交点为(m,n),则另一个交点为_________.
(6)设函数y=与y=x﹣1的图象的交点坐标为(a,b),则
QUOTE
的值为
(7)如图,RtΔABO的顶点A是双曲线与直线在第二象限的交点,
AB垂直轴于B,且S△ABO=,则反比例函数的解析式 .
(8)若反比例函数与一次函数y=3x+b都经过点(1,4),则kb=________.
(9)如图,已知A
(4,a),B
(-2,-4)是一次函数y=kx+b图象和反比例函数y=-
图象的交点.(1)求反比例函数和一次函数的解祈式;(2)求△A0B的面积.
(10)如图,在平面直角坐标系中,直线与双曲线在第一象限交于点A,与轴交于点C,AB⊥轴,垂足为B,且=1.求:(1)求两个函数解析式; (2)求△ABC的面积.
(11)平面直角坐标系中,直线AB交x轴于点A,交y轴于点B
且与反比例函数图象分别交于C、D两点,过点C作CM⊥x轴于M,AO=6,BO=3,CM=5.求直线AB的解析式和反比例函数解析式.
(五)反比例函数的应用:
例题讲解:
1.一个水池装水12立方米,如果从水管中每小时流出x立方米的水,经过y小时可以把水放完,那么y与x的函数关系式是________,自变量x的取值范围是________.
2.三角形的面积为6cm2,如果它的一边为ycm,这边上的高为xcm,那么y与x之间是________函数关系,以x为自变量的函数解析式为________.
3.长方体的体积为40cm3,此长方体的底面积y(cm2)与其对应高x(cm)之间的函数关系用图象大致可以表示为下面的(
).
4.下列各问题中两个变量之间的关系,不是反比例函数的是(
).
(A)小明完成百米赛跑时,所用时间t(s)与他的平均速度v(m/s)之间的关系
(B)长方形的面积为24,它的长y与宽x之间的关系
(C)压力为600N时,压强p(Pa)与受力面积S(m2)之间的关系
(D)一个容积为25L的容器中,所盛水的质量m(kg)与所盛水的体积V(L)之间的关系
5.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:
体积x(ml)
100
80
60
40
20
压强y(kpa)
60
75
100
150
300
则可以反映y与x之间的关系的式子是(
).
(A)y=3000x
(B)y=6000x
(C)
(D)
6.甲、乙两地间的公路长为300km,一辆汽车从甲地去乙地,汽车在途中的平均速度为V(km/h),到达时所用的时间为t(h),那么t是V________的函数,V关于t的函数关系式为________.
7.农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房(如图所示),则需要
塑料布y(m2)与半径R(m)的函数关系式是(不考虑塑料埋在土里的部分)________.
8.有一面积为60的梯形,其上底是下底长的三分之一,若下底长为x,高为y,
则y关于x的函数关系式是(
).
(A)
(B)
(C)
(D)
9.一个气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)写出这一函数的解析式;
(2)当气体体积为1m3时,气压是多少?
(3)当气球内的气压大于140kPa时,气球将爆炸,为了安全
起见,气体的体积应不小于多少?
10.某学校对教室采用药薰消毒法进行消毒.已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题图中所提供的信息解答下列问题:
(1)药物燃烧时y关于x的函数关系式为________,自变量x的取值范围是________;药物燃烧后y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量小于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过________分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
《反比例函数》巩固练习
一、选择题(本大题共10小题,每小题3分,共30分)
1.如果反比例函数的图象经过点,那么它还一定经过(
)
A.
B.
C.
D.
2.如图1,在平面直角坐标系中,点是轴正半轴上的一个定点,点是双曲线
上的一个动点,当点的横坐标逐渐增大时,的面积将(
)
A.逐渐增大
B.不变
C.逐渐减小
D.先增大,后减小
3.如果反比例函数的图象与直线没有交点,那么符合条件的值为(
)
A.
B.
C.
D.
4.在反比例函数的图象上有两个点,且,,则的取值范围是(
)
A.
B.
C.
D.
5.如图2,反比例函数与正比例函数的图象的一个交点坐标是,若,则的取值范围在数轴上表示为(
)
6.如图3,点是反比例函数图象上一点,过点作轴的平行线,交反比例函数的图象于点,连接,若的面积为2,则的值为(
)
A.
B.
C.
D.
7.设的一边长为,这条边上的高为,与满足的反比例函数关系如图4
所示,当为等腰直角三角形时,的值为(
)
A.
B.
C.
或
D.
或
8.在数学活动课上,小华借助下列表格中的数据,在平面直角坐标系中经历描点和连线
的步骤,正确绘制了某个反比例函数的图象,则下列关于该函数的描述错误的是(
)
A.图象在第二、四象限
B.图象必经过点
C.图象与坐标轴没有交点
D.当时,的取值范围是
9.如图5,点在反比例函数的图象上,且横坐标为2.若将点先向右平移两个单位,再向上平移一个单位后得到点,则在第一象限内,经过点的反比例函数图象的表达式是(
)
A.
B.
C.
D.
10.如图6,和的各顶点分别在双曲线,,的第一象限的图象上,,轴,轴,则(
)
A.
B.
C.
D.
二、填空题(本大题共10小题,每小题3分,共30分)
11.若梯形的下底长为,上底长为下底长的,高为,面积为60,则与的函数关系式是
(不考虑的取值范围).
12.如果关于的函数是反比例函数,那么的值等于
.
13.如图7,点是双曲线上的点,分别经过两点向轴、轴作垂线段,若,则
.
14.若反比例函数的函数图象过点,则与的大小关系是
.(填“>”或“=”“<”)
15.如图8,一次函数的图象与反比例函数的图象相交于两点,当时,,或,则一次函数的表达式为
.
16.在平面直角坐标系中,点的坐标为,点的坐标为,四边形为矩形,点为线段上的一个动点,若为等腰三角形,且点在双曲线上,则的值可以是
.
17.
如图9,已知双曲线,点为双曲线上的一点,且轴于点,轴于点,分别交双曲线于两点,
则的面积是
.
18.直线,与双曲线交于两点,
则
.
19.我们已经学习过反比例函数的图象和性质,请回顾研究它的过程,对函数进行探索,下列结论:
①图象在第一、二象限;
②图象在第一、三象限;
③图象关于轴对称;
④图象关于原点对称;
⑤当时,随增大而增大;当时,随增大而增大;
⑥当时,随增大而减小;当时,随增大而增大.
其中是函数的性质及它的图象特征的是
.(填写所有正确答案的序号)
20.如图10,在x轴的正半轴上依次截取,过点,分别作轴的垂线与反比例函数的图象相交于点,得直角三角形,,,,,并设其面积分别为,则的值为
,以此类推
(的整数).
三、解答题(本大题共6小题,共60分)
21.
(
8分)已知变量与成反比例函数,并且当时,.
(1)求与之间的函数关系式.
(2)求时,的值.
22.(10分)函数的图象如图11所示.
(1)在同一平面直角坐标系中,用描点法画下列函数的图象.
①;②.
列表:
画图象,并注明函数表达式.
(2)观察图象,完成填空:
①将函数的图象向
平移
个单位,可得函数的图象;
②将函数的图象向
平移
个单位,可得函数的图象.
(3)函数的图象经过怎样的变化,可得函数的图象?(写出一种即可)
23.
(
8分)如图12,已知一次函数(为常数)的图象与反比例函数(为常数,)的图象相交于点.
(1)求这两个函数的表达式及其图象的另一个交点的坐标.
(2)观察图象,写出使函数值的自变量的取值范围.
24.
(10分)如图13,在平面直角坐标系中,直线与双曲线相交于点和点.
(1)求直线与双曲线的表达式.
(2)对于横、纵坐标都是整数的点叫做整点.动点是双曲线上的整点,过点作垂直于轴的直线,交直线于点,当点位于点的下方时,请直接写出整点的坐标.
25.
(12分)一辆汽车匀速通过某段公路,所需时间(h)与行驶速度(km/h)满足函数关系式,其图象为如图14所示的一段曲线且端点为和.
(1)求和的值.
(2)若行驶速度不得超过60km/h,则汽车通过该路段最少需要多少时间?
26.
(12分)“保护生态环境,建设绿色社会”已经从理念变为人们的行动.某化工厂2017年1月的利润为200万元.设2017年1月为第1个月,第个月的利润为万元.由于排污超标,该厂决定从2017年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,与成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图15
).
(1)分别求该化工厂治污期间及治污改造工程完工后,与之间对应的函数关系式.
(2)治污改造工程完工后经过几个月,该厂月利润才能达到2017年1月的水平?
(3)当月利润少于100万元时,为该厂资金紧张期,问该厂资金紧张期共有几个月?
反
比例
函
数
P
y
x
O
M
N
图1
O
B
y
x
A
Q
图2
图6
O
A
C
B
M
y
N
x
O
图4
P
y
M
x
0
N
图3
图5
图7
(第(7)题)
一
份
汗
水
一
分
收
获,付
出
才
有
回
报
!
1
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
