2020-2021学年华东师大版九年级数学下册28.2.1简单随机抽样-课件(22张PPT)
文档属性
| 名称 | 2020-2021学年华东师大版九年级数学下册28.2.1简单随机抽样-课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 14:03:10 | ||
图片预览







文档简介
(共22张PPT)
第28章
样本与总体
28.2
用样本估计总体
博学
慎思
求真
至善
1.简单随机抽样
2.
简单随机抽样调查可靠吗
教学目标
教学重点与难点
重点:理解简单随机抽样,掌握抽样调查的方法.
难点:理解简单随机抽样调查的可靠性.
1.会用简单随机抽样的方法确定样本的个体.
2.知道抽样调查的方法是科学的、可靠的.
合适的抽样调查应具备以下几点:
1.要调查的对象在总体中必须有
;
2.调查的样本容量要
;
3.开展调查之前,要仔细检查总体中的
是否都有可能成为调查对象;
4.仅仅增加调查对象
不一定能够提高调查的
质量.
温故夯基
代表性
足够大
每个个体
数量
巩固练习
判断下列抽样调查选取样本的方法是否合适,并说明理由:
1.某手表厂想要了解6~11岁少年儿童戴手表的比例,周末
来到一家业余艺术学校,对在那里学习的200名学生进行
调查;
2.为了考察“6”是否是最难掷出的一个数,小明投掷了6次
正方体骰子;
3.调查一个班级里学号为6的倍数的学生,以了解学生对
班主任老师某项新举措的意见和建议;
4.某环保网站对“支持商店使用环保购物袋的程度”进行
在线调查.
不合适.
样本不具有代表性.
不合适.
样本的容量过小.
合适.
样本具有代表性.
样本不具有代表性.
不合适.
新知导入
1.妈妈为了知道饼熟了没有,从刚出锅的饼上切下一小块尝尝,如果这一小块饼熟了,那么可以估计整张饼也熟了.
2.环境检测中心为了解一个城市的空气质量情况,会在这个城市中分散地选定几个点,从这些地点采集数据.对这些数据进行分析,就可以估计整个城市的空气质量.
3.农科站为了解农田中某种病虫害的灾情,会随机地选定几块地,仔细检查这几块地的虫卵数,然后估计一公顷农田大约平均有多少虫卵,会不会发生大规模的病虫害.
以上三个例子,你知道其中的原因吗?
以上几个例子说明:为了解某些情况或得到某些结论,
有时不适合作普查,而需要作抽样调查.
我们知道:样本要有代表性,没有偏向,这样的抽样调查
才能较好地反映总体的情况.
如何进行抽样才比较科学呢?
学习新知
一.简单随机抽样
1.简单随机抽样的定义:要使样本具有代表性,不偏向总体
中的某些个体,有一个对每个个体都公平的办法,那就是
用抽签的办法决定哪些个体进入样本.
统计学家称这种理想的抽样方法为简单随机抽样.
2.简单随机抽样的方法(抽签法):
(1)先将每个个体编号;
(2)将写有这些编号的纸条全部放入一个盒子,
搅拌均匀;
(3)再用抽签的办法,
抽出一个编号,
那个编号的个体就
被选入样本.
例题精析
例
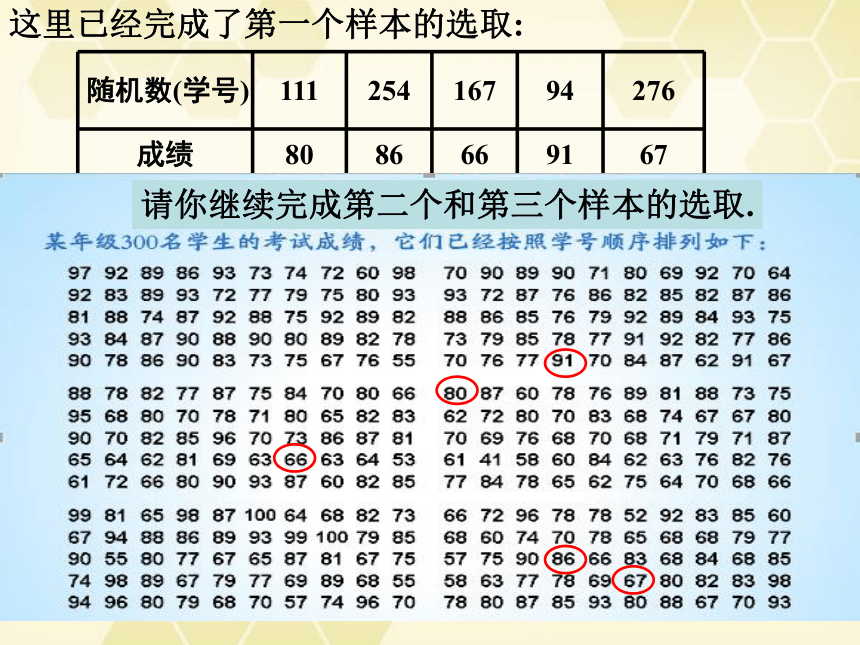
假设总体是某年级300名学生的考试成绩,已经把它们
按照学号顺序排列如下:(每行有20个数据)
用简单随机抽样方法抽取三个样本,每个样本含有5个个体.
这里已经完成了第一个样本的选取:
随机数(学号)
111
254
167
94
276
成绩
80
86
66
91
67
请你继续完成第二个和第三个样本的选取.
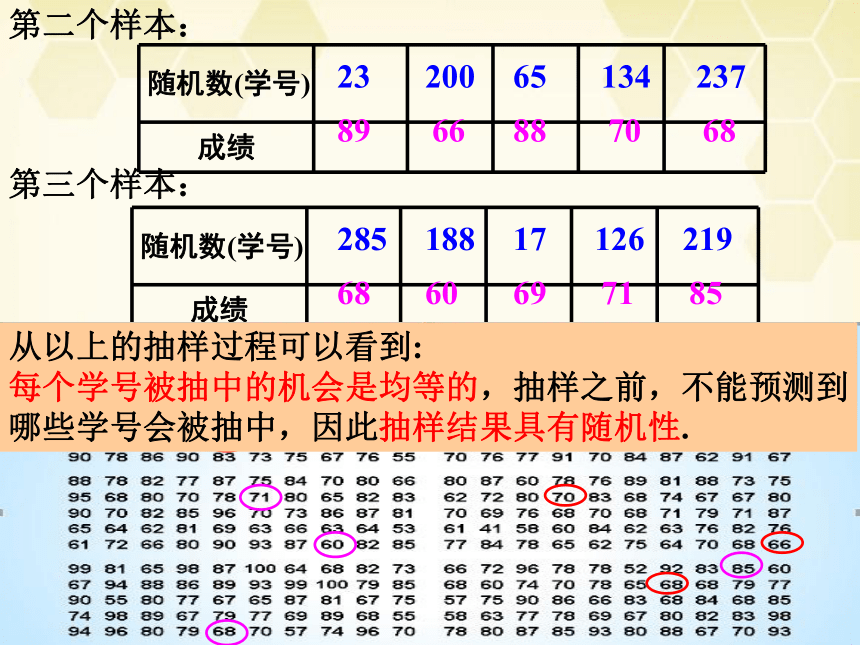
第二个样本:
第三个样本:
随机数(学号)
成绩
随机数(学号)
成绩
23
89
200
65
134
237
66
88
70
68
285
188
17
126
219
68
60
69
71
85
从以上的抽样过程可以看到:
每个学号被抽中的机会是均等的,抽样之前,不能预测到
哪些学号会被抽中,因此抽样结果具有随机性.
1.为了解全校学生的视力情况,采用了下列调查方法,
其中为简单随机抽样的是(
).
A.从九年级每个班级中任意抽取10人作调查
B.查阅全校所有学生的体检表
C.对每个班学号为1,11,21,31,41的学生作调查
D.从每个班中任意抽取5人作调查
随堂练习
D
2.有四位同学从编号为1~50的总体中抽取8个个体组成
一个样本,他们选取的样本中个体编号分别为:
①
5,10,15,20,25,30,35,40;
②
43,44,45,46,47,48,49,50;
③
1,3,5,7,9,11,13,15;
④
40,25,12,17,35,29,24,19.
你认为较具有随机性的样本是______(填序号).
④
学习新知
二.简单随机抽样调查可靠吗
仍以这300名学生的考试成绩为例,考察抽样调查的结果
是否与总体的情况一致.
(1)对总体情况进行分析,根据已知数据,按照10分的距离将
成绩分段,统计每个分数段学生出现的频数,列表如下:
成绩段
39.5~49.5
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100
频数
1
9
62
85
96
47
频数分布表
(2)根据上表绘制直方图,如下:
0
20
40
60
80
100
120
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
利用原始数据可以算出总体的平均数为78.1,方差为116.3.
成绩段
39.5~49.5
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100
频数
1
9
62
85
96
47
从图表中可以看出:
分到
分
的学生数最多;
90分以上的学生数
较少,不及格学生数
最少.
79.5
89.5
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
(3)根据前面获取的三个样本,分别绘制频数分布直方图,计算出平均数和方差.
随机数(学号)
111
254
167
94
276
成绩
80
86
66
91
67
第一个样本:
平均数为:
,方差为:
.
78
100.4
随机数(学号)
23
200
65
134
237
成绩
89
66
88
70
68
第二个样本:
(3)根据前面获取的三个样本,分别绘制频数分布直方图,计算出平均数和方差.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
平均数为:
,方差为:
.
76.2
102.56
第三个样本:
(3)根据前面获取的三个样本,分别绘制频数分布直方图,计算出平均数和方差.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
平均数为:
,方差为:
.
随机数(学号)
285
188
17
126
219
成绩
68
60
69
71
85
70.6
68.84
这三张样本频数分布直方图与总体频数分布直方图相像吗?
不相像
样本的平均数和方差与总体的平均数和方差接近吗?
总体的平均数为78.1,方差为116.3.
样本一平均数为78,方差为100.4,
样本二平均数为76.2,方差为102.56,
样本三平均数为70.6,方差为68.84.
不同样本的平均数与方差差异较大,什么因素造成的呢?
所取样本的容量太小
(4)用简单随机抽样的方法,获取两个样本容量为10的样本,绘制频数分布直方图,计算平均数和方差.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本一:
平均数为:79.7,方差为:88.41.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本二:
平均数为:83.3,方差为:132.61.
总体的平均数为78.1,方差为116.3.
比较接近总体的平均数和方差
0
4
8
12
16
20
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
(5)用简单随机抽样的方法,获取两个样本容量为40的样本,绘制频数分布直方图,计算平均数和方差.
样本一:
平均数为:75.65,方差为:103.5275.
0
4
8
12
16
20
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本二:
平均数为:77.1,方差为:114.49.
总体的平均数为78.1,方差为116.3.
你有什么发现?
随着样本容量的增加,样本的
平均数和方差有接近于总体
的平均数和方差的趋势.
由简单随机抽样获得样本容量较大的样本,可以用
样本平均数和方差估计总体平均数和总体方差.
大样本更容易
认识总体的真面目
1.某大学为了了解法学院1500名新生的身高情况,采用随机调查的方式用300名新生的身高为样本进行统计,其中身高在170cm~175cm的有75人,那么估计法学院新生身高在170cm~175cm的人数约是(
).
A.
300
B.
325
C.
375
D.
450
2.小芳家今年3月份头6天的用电量如下表:
日期
1日
2日
3日
4日
5日
6日
用电量(度)
3.5
4.6
5.2
4.1
3.4
3.2
请你用统计知识,估计小芳家3月份总用电量是(
).
A.
152
B.
124
C.
96
D.
103
C
B
随堂练习
每天平均用电量为
.
4
随堂练习
3.质检部门为了检测某品牌电器的质量,从同一批次共
10000件产品中随机抽取100件进行检测,检测出次品5件.
由此估计这一批次产品中的次品件数是(
).
A.
50??
??????
B.
100?????
??????
?C.
500????
??????
?D.
10000
C
4.某区有1000名学生参加数学考试,从中抽出部分数学成绩
来分析,抽出的成绩中96分的20人,
90分的10人,
80分的
20人,可以估计总体平均分为(
).
A.
88.4
分
B.
86分
C.
90分
D.
92分
A
(96×20+90×10+80×20)÷50=
88.4
5.某养鱼专业户为了估计湖里有多少条鱼,先捕上100条做
上标记,然后放回到湖里,过一段时间待带标记的鱼完全混
合于鱼群后,再捕上200条鱼,发现其中带标记的鱼有20条,
湖里大约有
条鱼.
设湖里大约有x条鱼,
则
100:x=20:200.
1000
一.简单随机抽样
1.简单随机抽样的定义:要使样本具有代表性,不偏向总体
中的某些个体,有一个对每个个体都公平的办法,那就是
用抽签的办法决定哪些个体进入样本.
统计学家称这种理想的抽样方法为简单随机抽样.
2.简单随机抽样的方法(抽签法):
(1)先将每个个体编号;
(2)将写有这些编号的纸条全部放入一个盒子,
搅拌均匀;
(3)再用抽签的办法,
抽出一个编号,
那个编号的个体就
被选入样本.
课堂小结
二.样本估计总体
由简单随机抽样获得样本容量较大的样本,可以用样本平均数和方差估计总体平均数和总体方差.
作业与课外学习任务
1.作业:课本P92
习题28.2
1,2,3,4
练习:学习检测
P50-53
1~16
2.课外学习任务:
预习课本P94-99
28.3
借助调查做决策
1.借助调查做决策
教学反馈:
作业存在的主要问题:
第28章
样本与总体
28.2
用样本估计总体
博学
慎思
求真
至善
1.简单随机抽样
2.
简单随机抽样调查可靠吗
教学目标
教学重点与难点
重点:理解简单随机抽样,掌握抽样调查的方法.
难点:理解简单随机抽样调查的可靠性.
1.会用简单随机抽样的方法确定样本的个体.
2.知道抽样调查的方法是科学的、可靠的.
合适的抽样调查应具备以下几点:
1.要调查的对象在总体中必须有
;
2.调查的样本容量要
;
3.开展调查之前,要仔细检查总体中的
是否都有可能成为调查对象;
4.仅仅增加调查对象
不一定能够提高调查的
质量.
温故夯基
代表性
足够大
每个个体
数量
巩固练习
判断下列抽样调查选取样本的方法是否合适,并说明理由:
1.某手表厂想要了解6~11岁少年儿童戴手表的比例,周末
来到一家业余艺术学校,对在那里学习的200名学生进行
调查;
2.为了考察“6”是否是最难掷出的一个数,小明投掷了6次
正方体骰子;
3.调查一个班级里学号为6的倍数的学生,以了解学生对
班主任老师某项新举措的意见和建议;
4.某环保网站对“支持商店使用环保购物袋的程度”进行
在线调查.
不合适.
样本不具有代表性.
不合适.
样本的容量过小.
合适.
样本具有代表性.
样本不具有代表性.
不合适.
新知导入
1.妈妈为了知道饼熟了没有,从刚出锅的饼上切下一小块尝尝,如果这一小块饼熟了,那么可以估计整张饼也熟了.
2.环境检测中心为了解一个城市的空气质量情况,会在这个城市中分散地选定几个点,从这些地点采集数据.对这些数据进行分析,就可以估计整个城市的空气质量.
3.农科站为了解农田中某种病虫害的灾情,会随机地选定几块地,仔细检查这几块地的虫卵数,然后估计一公顷农田大约平均有多少虫卵,会不会发生大规模的病虫害.
以上三个例子,你知道其中的原因吗?
以上几个例子说明:为了解某些情况或得到某些结论,
有时不适合作普查,而需要作抽样调查.
我们知道:样本要有代表性,没有偏向,这样的抽样调查
才能较好地反映总体的情况.
如何进行抽样才比较科学呢?
学习新知
一.简单随机抽样
1.简单随机抽样的定义:要使样本具有代表性,不偏向总体
中的某些个体,有一个对每个个体都公平的办法,那就是
用抽签的办法决定哪些个体进入样本.
统计学家称这种理想的抽样方法为简单随机抽样.
2.简单随机抽样的方法(抽签法):
(1)先将每个个体编号;
(2)将写有这些编号的纸条全部放入一个盒子,
搅拌均匀;
(3)再用抽签的办法,
抽出一个编号,
那个编号的个体就
被选入样本.
例题精析
例
假设总体是某年级300名学生的考试成绩,已经把它们
按照学号顺序排列如下:(每行有20个数据)
用简单随机抽样方法抽取三个样本,每个样本含有5个个体.
这里已经完成了第一个样本的选取:
随机数(学号)
111
254
167
94
276
成绩
80
86
66
91
67
请你继续完成第二个和第三个样本的选取.
第二个样本:
第三个样本:
随机数(学号)
成绩
随机数(学号)
成绩
23
89
200
65
134
237
66
88
70
68
285
188
17
126
219
68
60
69
71
85
从以上的抽样过程可以看到:
每个学号被抽中的机会是均等的,抽样之前,不能预测到
哪些学号会被抽中,因此抽样结果具有随机性.
1.为了解全校学生的视力情况,采用了下列调查方法,
其中为简单随机抽样的是(
).
A.从九年级每个班级中任意抽取10人作调查
B.查阅全校所有学生的体检表
C.对每个班学号为1,11,21,31,41的学生作调查
D.从每个班中任意抽取5人作调查
随堂练习
D
2.有四位同学从编号为1~50的总体中抽取8个个体组成
一个样本,他们选取的样本中个体编号分别为:
①
5,10,15,20,25,30,35,40;
②
43,44,45,46,47,48,49,50;
③
1,3,5,7,9,11,13,15;
④
40,25,12,17,35,29,24,19.
你认为较具有随机性的样本是______(填序号).
④
学习新知
二.简单随机抽样调查可靠吗
仍以这300名学生的考试成绩为例,考察抽样调查的结果
是否与总体的情况一致.
(1)对总体情况进行分析,根据已知数据,按照10分的距离将
成绩分段,统计每个分数段学生出现的频数,列表如下:
成绩段
39.5~49.5
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100
频数
1
9
62
85
96
47
频数分布表
(2)根据上表绘制直方图,如下:
0
20
40
60
80
100
120
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
利用原始数据可以算出总体的平均数为78.1,方差为116.3.
成绩段
39.5~49.5
49.5~59.5
59.5~69.5
69.5~79.5
79.5~89.5
89.5~100
频数
1
9
62
85
96
47
从图表中可以看出:
分到
分
的学生数最多;
90分以上的学生数
较少,不及格学生数
最少.
79.5
89.5
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
(3)根据前面获取的三个样本,分别绘制频数分布直方图,计算出平均数和方差.
随机数(学号)
111
254
167
94
276
成绩
80
86
66
91
67
第一个样本:
平均数为:
,方差为:
.
78
100.4
随机数(学号)
23
200
65
134
237
成绩
89
66
88
70
68
第二个样本:
(3)根据前面获取的三个样本,分别绘制频数分布直方图,计算出平均数和方差.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
平均数为:
,方差为:
.
76.2
102.56
第三个样本:
(3)根据前面获取的三个样本,分别绘制频数分布直方图,计算出平均数和方差.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
平均数为:
,方差为:
.
随机数(学号)
285
188
17
126
219
成绩
68
60
69
71
85
70.6
68.84
这三张样本频数分布直方图与总体频数分布直方图相像吗?
不相像
样本的平均数和方差与总体的平均数和方差接近吗?
总体的平均数为78.1,方差为116.3.
样本一平均数为78,方差为100.4,
样本二平均数为76.2,方差为102.56,
样本三平均数为70.6,方差为68.84.
不同样本的平均数与方差差异较大,什么因素造成的呢?
所取样本的容量太小
(4)用简单随机抽样的方法,获取两个样本容量为10的样本,绘制频数分布直方图,计算平均数和方差.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本一:
平均数为:79.7,方差为:88.41.
0
1
2
3
4
5
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本二:
平均数为:83.3,方差为:132.61.
总体的平均数为78.1,方差为116.3.
比较接近总体的平均数和方差
0
4
8
12
16
20
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
(5)用简单随机抽样的方法,获取两个样本容量为40的样本,绘制频数分布直方图,计算平均数和方差.
样本一:
平均数为:75.65,方差为:103.5275.
0
4
8
12
16
20
39.5
49.5
59.5
69.5
79.5
89.5
100
人数
成绩
样本二:
平均数为:77.1,方差为:114.49.
总体的平均数为78.1,方差为116.3.
你有什么发现?
随着样本容量的增加,样本的
平均数和方差有接近于总体
的平均数和方差的趋势.
由简单随机抽样获得样本容量较大的样本,可以用
样本平均数和方差估计总体平均数和总体方差.
大样本更容易
认识总体的真面目
1.某大学为了了解法学院1500名新生的身高情况,采用随机调查的方式用300名新生的身高为样本进行统计,其中身高在170cm~175cm的有75人,那么估计法学院新生身高在170cm~175cm的人数约是(
).
A.
300
B.
325
C.
375
D.
450
2.小芳家今年3月份头6天的用电量如下表:
日期
1日
2日
3日
4日
5日
6日
用电量(度)
3.5
4.6
5.2
4.1
3.4
3.2
请你用统计知识,估计小芳家3月份总用电量是(
).
A.
152
B.
124
C.
96
D.
103
C
B
随堂练习
每天平均用电量为
.
4
随堂练习
3.质检部门为了检测某品牌电器的质量,从同一批次共
10000件产品中随机抽取100件进行检测,检测出次品5件.
由此估计这一批次产品中的次品件数是(
).
A.
50??
??????
B.
100?????
??????
?C.
500????
??????
?D.
10000
C
4.某区有1000名学生参加数学考试,从中抽出部分数学成绩
来分析,抽出的成绩中96分的20人,
90分的10人,
80分的
20人,可以估计总体平均分为(
).
A.
88.4
分
B.
86分
C.
90分
D.
92分
A
(96×20+90×10+80×20)÷50=
88.4
5.某养鱼专业户为了估计湖里有多少条鱼,先捕上100条做
上标记,然后放回到湖里,过一段时间待带标记的鱼完全混
合于鱼群后,再捕上200条鱼,发现其中带标记的鱼有20条,
湖里大约有
条鱼.
设湖里大约有x条鱼,
则
100:x=20:200.
1000
一.简单随机抽样
1.简单随机抽样的定义:要使样本具有代表性,不偏向总体
中的某些个体,有一个对每个个体都公平的办法,那就是
用抽签的办法决定哪些个体进入样本.
统计学家称这种理想的抽样方法为简单随机抽样.
2.简单随机抽样的方法(抽签法):
(1)先将每个个体编号;
(2)将写有这些编号的纸条全部放入一个盒子,
搅拌均匀;
(3)再用抽签的办法,
抽出一个编号,
那个编号的个体就
被选入样本.
课堂小结
二.样本估计总体
由简单随机抽样获得样本容量较大的样本,可以用样本平均数和方差估计总体平均数和总体方差.
作业与课外学习任务
1.作业:课本P92
习题28.2
1,2,3,4
练习:学习检测
P50-53
1~16
2.课外学习任务:
预习课本P94-99
28.3
借助调查做决策
1.借助调查做决策
教学反馈:
作业存在的主要问题:
