2020-2021学年人教版数学七年级下册5.2.2平行线的判定-课件(15张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册5.2.2平行线的判定-课件(15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 14:10:22 | ||
图片预览


文档简介
(共15张PPT)
同旁内角互补,两直线平行
人教版数学-七年级下册
5.2
平行线及其判定
先来回顾一下我们前面学习的一些知识!
复习引入:
探索新知:
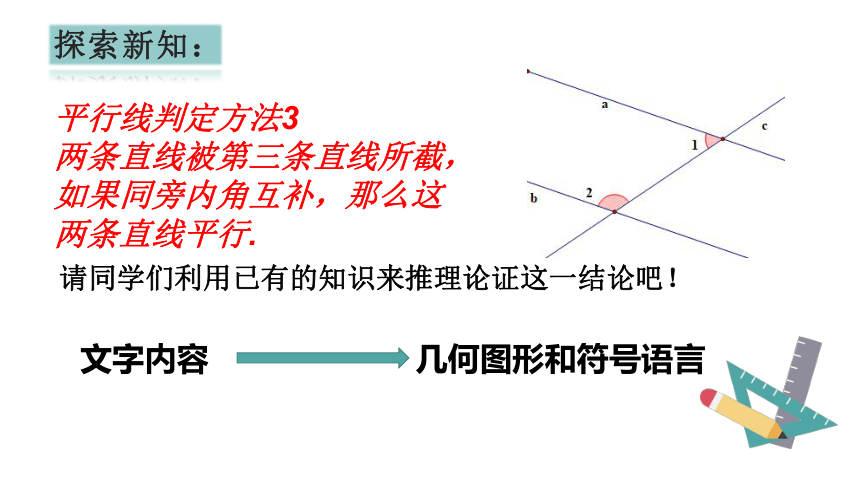
平行线判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
请同学们利用已有的知识来推理论证这一结论吧!
文字内容
几何图形和符号语言
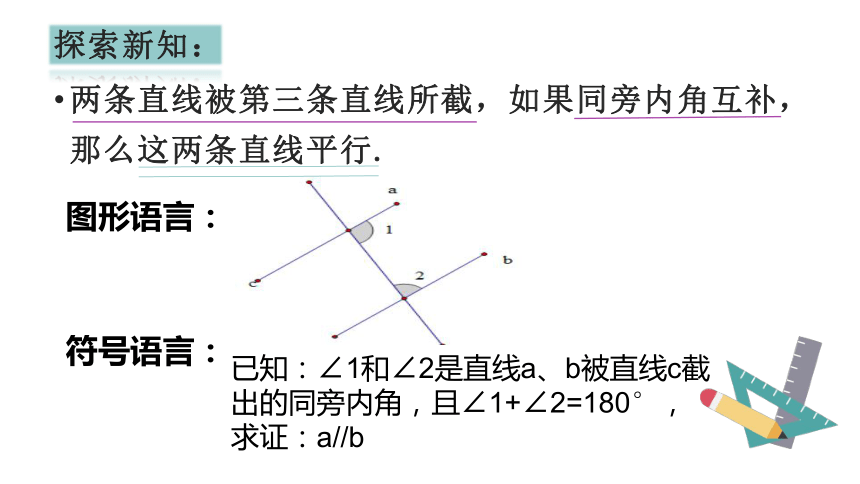
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
探索新知:
图形语言:
符号语言:
已知:∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1+∠2=180°,
求证:a//b
探索新知:
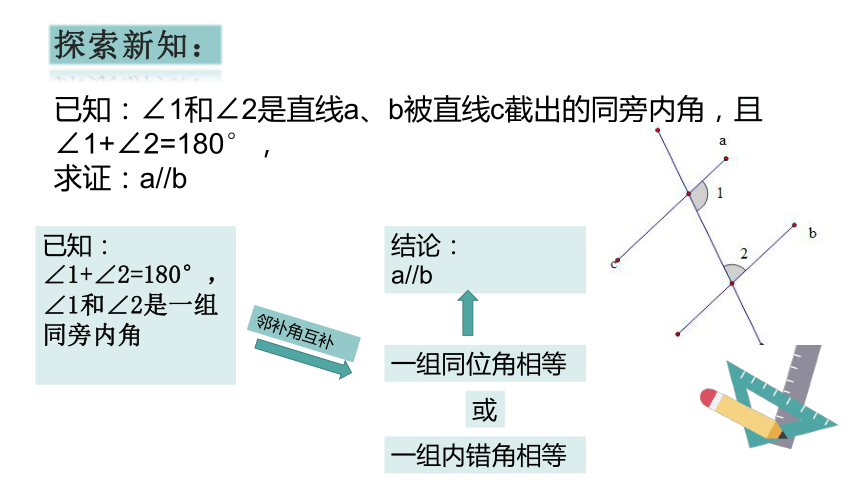
已知:∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1+∠2=180°,
求证:a//b
已知:
∠1+∠2=180°,∠1和∠2是一组同旁内角
结论:
a//b
一组同位角相等
一组内错角相等
或
邻补角互补
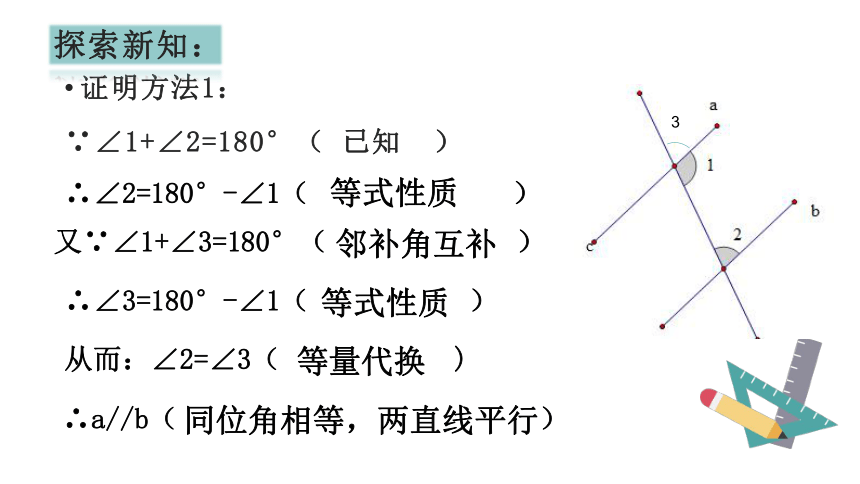
证明方法1:
∵∠1+∠2=180°(
已知
)
探索新知:
3
∴∠2=180°-∠1(
)
又∵∠1+∠3=180°(
)
∴∠3=180°-∠1(
)
从而:∠2=∠3(
)
∴a//b(
)
等式性质
邻补角互补
同位角相等,两直线平行
等量代换
等式性质
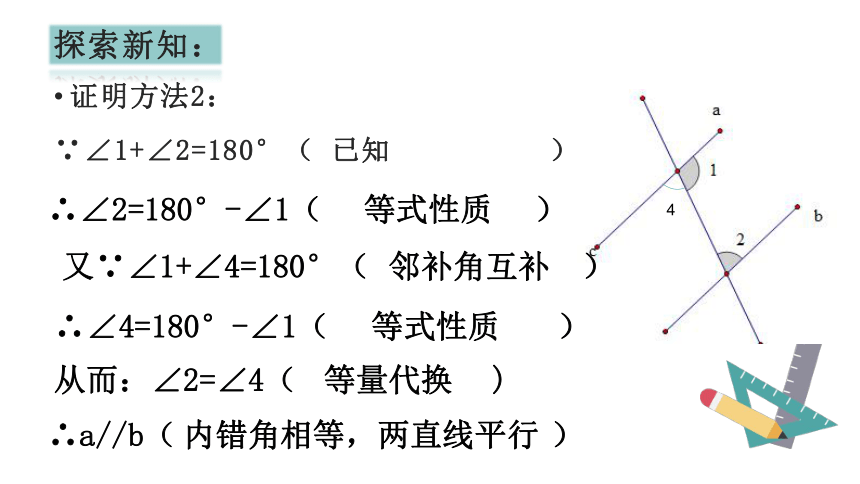
证明方法2:
∵∠1+∠2=180°(
已知
)
探索新知:
4
∴∠2=180°-∠1(
)
又∵∠1+∠4=180°(
)
∴∠4=180°-∠1(
)
从而:∠2=∠4(
)
∴a//b(
)
等式性质
邻补角互补
等式性质
等量代换
内错角相等,两直线平行
探索新知:
“内错角相等,
两直线平行”
“同旁内角互补,
两直线平行”
已
知(或是已解决的问题)
未
知
转
化
“同位角相等,
两直线平行”
例
:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
应用新知:
请同学们试一试,将命题的文字语言转化成几何图形和符号语言?
应用新知:
已知:如图:b⊥a,c⊥a,求证:b//c
已知:
b⊥a,c⊥a,
结论:
b//c
一组同位角相等
一组内错角相等
或
或
一组同旁内角互补
应用新知:
已知:如图:b⊥a,c⊥a,求证:b//c
证明方法1:
∵b⊥a,c⊥a(已知)
∴∠1=90°,∠2=90°(
)
从而:∠1=∠2(
)
∴b//c(
)
垂直的定义
等量代换
同位角相等,两直线平行
应用新知:
已知:如图:b⊥a,c⊥a,求证:b//c
证明方法2:∵b⊥a,c⊥a(已知)∴∠1=90°,∠4=90°(
)
垂直的定义
从而:∠1=∠4
∴b//c(
)
内错角相等,两直线平行
应用新知:
已知:如图:b⊥a,c⊥a,求证:b//c
证明方法3:∵b⊥a,c⊥a(已知)∴∠1=90°,∠3=90°(
)
垂直的定义
从而:∠1+∠3=180°
∴b//c(
)
同旁内角互补,两直线平行
小结:
方法小结:
“同位角相等,
两直线平行”
“内错角相等,
两直线平行”
“同旁内角互补,
两直线平行”
已
知(或是已解决的问题)
未
知
转
化
知识小结:
数学是研究现实生活中数量关系和空间形式的数学。
——恩格斯
同旁内角互补,两直线平行
人教版数学-七年级下册
5.2
平行线及其判定
先来回顾一下我们前面学习的一些知识!
复习引入:
探索新知:
平行线判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
请同学们利用已有的知识来推理论证这一结论吧!
文字内容
几何图形和符号语言
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
探索新知:
图形语言:
符号语言:
已知:∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1+∠2=180°,
求证:a//b
探索新知:
已知:∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1+∠2=180°,
求证:a//b
已知:
∠1+∠2=180°,∠1和∠2是一组同旁内角
结论:
a//b
一组同位角相等
一组内错角相等
或
邻补角互补
证明方法1:
∵∠1+∠2=180°(
已知
)
探索新知:
3
∴∠2=180°-∠1(
)
又∵∠1+∠3=180°(
)
∴∠3=180°-∠1(
)
从而:∠2=∠3(
)
∴a//b(
)
等式性质
邻补角互补
同位角相等,两直线平行
等量代换
等式性质
证明方法2:
∵∠1+∠2=180°(
已知
)
探索新知:
4
∴∠2=180°-∠1(
)
又∵∠1+∠4=180°(
)
∴∠4=180°-∠1(
)
从而:∠2=∠4(
)
∴a//b(
)
等式性质
邻补角互补
等式性质
等量代换
内错角相等,两直线平行
探索新知:
“内错角相等,
两直线平行”
“同旁内角互补,
两直线平行”
已
知(或是已解决的问题)
未
知
转
化
“同位角相等,
两直线平行”
例
:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
应用新知:
请同学们试一试,将命题的文字语言转化成几何图形和符号语言?
应用新知:
已知:如图:b⊥a,c⊥a,求证:b//c
已知:
b⊥a,c⊥a,
结论:
b//c
一组同位角相等
一组内错角相等
或
或
一组同旁内角互补
应用新知:
已知:如图:b⊥a,c⊥a,求证:b//c
证明方法1:
∵b⊥a,c⊥a(已知)
∴∠1=90°,∠2=90°(
)
从而:∠1=∠2(
)
∴b//c(
)
垂直的定义
等量代换
同位角相等,两直线平行
应用新知:
已知:如图:b⊥a,c⊥a,求证:b//c
证明方法2:∵b⊥a,c⊥a(已知)∴∠1=90°,∠4=90°(
)
垂直的定义
从而:∠1=∠4
∴b//c(
)
内错角相等,两直线平行
应用新知:
已知:如图:b⊥a,c⊥a,求证:b//c
证明方法3:∵b⊥a,c⊥a(已知)∴∠1=90°,∠3=90°(
)
垂直的定义
从而:∠1+∠3=180°
∴b//c(
)
同旁内角互补,两直线平行
小结:
方法小结:
“同位角相等,
两直线平行”
“内错角相等,
两直线平行”
“同旁内角互补,
两直线平行”
已
知(或是已解决的问题)
未
知
转
化
知识小结:
数学是研究现实生活中数量关系和空间形式的数学。
——恩格斯
