2020-2021学年人教版数学七年级下册6.2 立方根 课件(21张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册6.2 立方根 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
6.2
立方根
学习目标:
1、能记住立方根的概念,会用根号表示一个数的立方根.
2、知道开立方与立方互为逆运算,会用立方运算求某些数的立方根.
3、能记住正数、负数、0的立方根的特点
4、区分立方根与平方根的不同.
学习重点:
学习立方根的概念和求法.
学习难点:
立方根和平方根的区别
64的平方根是______
-100的平方根是________
0的平方根是________
没有平方根
0
一个正数有正负两个平方根,它们互为相反数;
零的平方根是零,负数没有平方根.
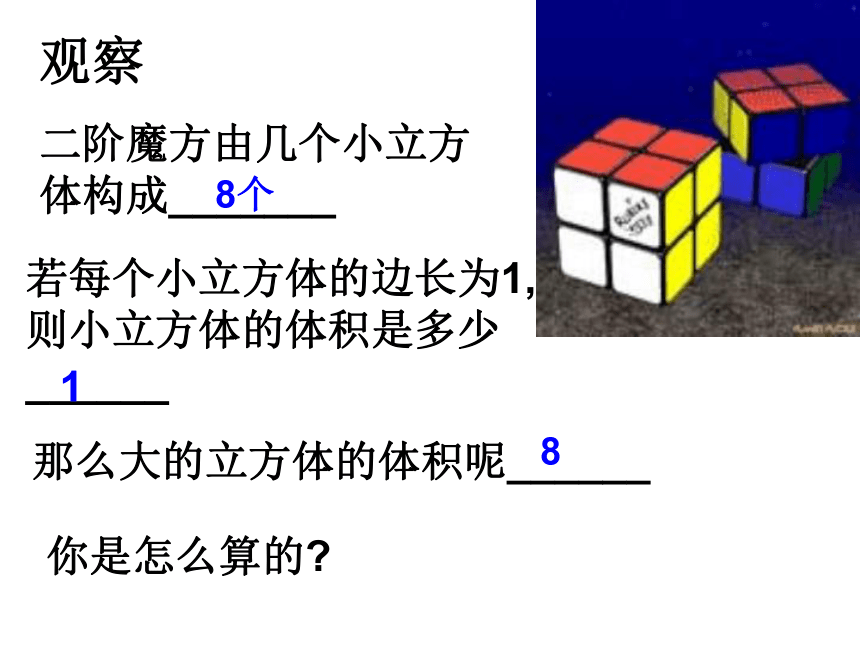
观察
二阶魔方由几个小立方体构成_______
若每个小立方体的边长为1,则小立方体的体积是多少______
你是怎么算的?
8个
1
8
那么大的立方体的体积呢______
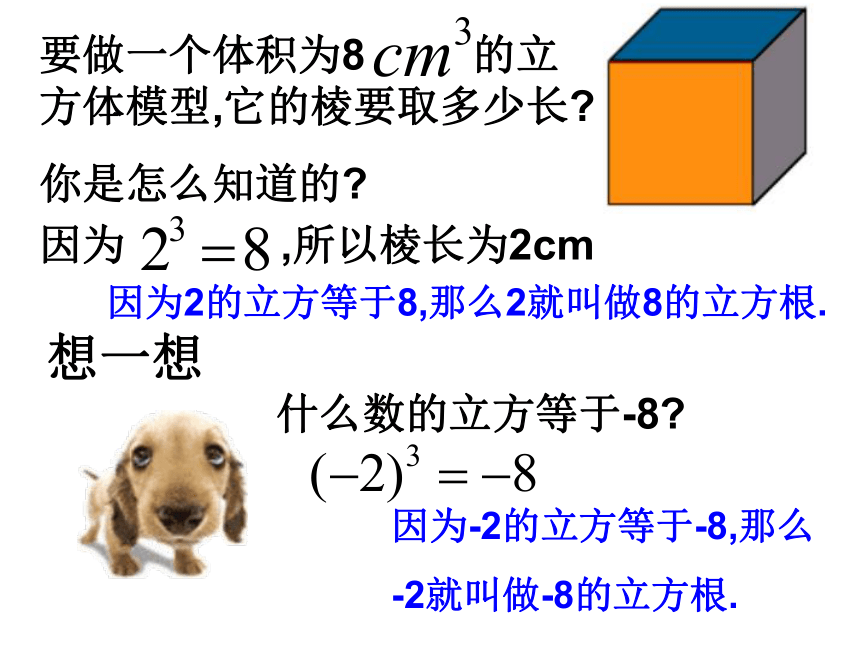
要做一个体积为8
的立方体模型,它的棱要取多少长?
你是怎么知道的?
因为
,所以棱长为2cm
什么数的立方等于-8?
想一想
因为2的立方等于8,那么2就叫做8的立方根.
因为-2的立方等于-8,那么
-2就叫做-8的立方根.
什么才是一个数a的立方根呢?
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.若x3=a,那么x
叫做a
的立方根.记做 .
3
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
求一个数的立方根的运算,叫做开立方.
3
3
=2
=
-2
3不能省
开立方运算
立方运算
互为逆运算
小露一手
返回
例1 求下列各数的立方根
(1)
27
(2)-27
(3)
0
解:
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(3)
0
解
∵0
=0
∴0的立方根是0
正数有立方根吗?如果有,有几个?
想一想
负数呢?
零呢?
从上面的例1可知:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
练一练
1.判断下列说法是否正确,并说明理由
(1)
x
(2)
25的平方根是5
x
(3)
-64没有立方根
x
(4)
-4的平方根是
x
(5)
0的平方根和立方根都是0
√
你真棒!
这是送你的!
2
填空:
5
5
3
3.下列各式是否有意义?为什么?
(1)
(2)
(3)
(4)
4.抢答
运用新知
例2 求下列各式的值
:
例3.求下列各式中的
(1)
(2)
(3)
(1)解:
(3)解:
(2)解:
想一想1
立方根是它本身的数有那些?
有1,
-1,
0
平方根是它本身的数呢?
只有0
探究
先填写下表,再回答问题:
a
0.000001
0.001
1
1000
1000000
0.01
0.1
1
10
100
从上面表格中你发现什么?
当被开方数的小数点移动三位时,立方根的小数点移动一位。
平方根
立方根
定
义
性
质
正
数
0
负
数
开
方
表
示
如果一个数的平方等于a,
那么这个数就叫a的平方根。
如果一个数的立方等于a,
那么这个数就叫a的立方根。
有两个平方根,
互为相反数
有一个平方根,是0
没有平方根
求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。
,其中a
是被开方数,
2是根指数(省略)
求一个数的立方根的运算
叫开立方;开立方与立方
是互逆运算。
有一个立方根,也是负数
有一个立方根,是0
有一个立方根,也是正数
,其中a
是被开方数,
3是根指数(不能省略)
讨论:你能归纳出平方根和立方根的异同点吗?
课堂小结:
1、立方根和开立方的定义.
2、正数、0、负数的立方根的特征.
3、立方根与平方根的异同.
4、你还有什么疑惑?
作业布置:
P52
习题6.2
第3,5题
6.2
立方根
学习目标:
1、能记住立方根的概念,会用根号表示一个数的立方根.
2、知道开立方与立方互为逆运算,会用立方运算求某些数的立方根.
3、能记住正数、负数、0的立方根的特点
4、区分立方根与平方根的不同.
学习重点:
学习立方根的概念和求法.
学习难点:
立方根和平方根的区别
64的平方根是______
-100的平方根是________
0的平方根是________
没有平方根
0
一个正数有正负两个平方根,它们互为相反数;
零的平方根是零,负数没有平方根.
观察
二阶魔方由几个小立方体构成_______
若每个小立方体的边长为1,则小立方体的体积是多少______
你是怎么算的?
8个
1
8
那么大的立方体的体积呢______
要做一个体积为8
的立方体模型,它的棱要取多少长?
你是怎么知道的?
因为
,所以棱长为2cm
什么数的立方等于-8?
想一想
因为2的立方等于8,那么2就叫做8的立方根.
因为-2的立方等于-8,那么
-2就叫做-8的立方根.
什么才是一个数a的立方根呢?
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.若x3=a,那么x
叫做a
的立方根.记做 .
3
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
求一个数的立方根的运算,叫做开立方.
3
3
=2
=
-2
3不能省
开立方运算
立方运算
互为逆运算
小露一手
返回
例1 求下列各数的立方根
(1)
27
(2)-27
(3)
0
解:
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(3)
0
解
∵0
=0
∴0的立方根是0
正数有立方根吗?如果有,有几个?
想一想
负数呢?
零呢?
从上面的例1可知:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
练一练
1.判断下列说法是否正确,并说明理由
(1)
x
(2)
25的平方根是5
x
(3)
-64没有立方根
x
(4)
-4的平方根是
x
(5)
0的平方根和立方根都是0
√
你真棒!
这是送你的!
2
填空:
5
5
3
3.下列各式是否有意义?为什么?
(1)
(2)
(3)
(4)
4.抢答
运用新知
例2 求下列各式的值
:
例3.求下列各式中的
(1)
(2)
(3)
(1)解:
(3)解:
(2)解:
想一想1
立方根是它本身的数有那些?
有1,
-1,
0
平方根是它本身的数呢?
只有0
探究
先填写下表,再回答问题:
a
0.000001
0.001
1
1000
1000000
0.01
0.1
1
10
100
从上面表格中你发现什么?
当被开方数的小数点移动三位时,立方根的小数点移动一位。
平方根
立方根
定
义
性
质
正
数
0
负
数
开
方
表
示
如果一个数的平方等于a,
那么这个数就叫a的平方根。
如果一个数的立方等于a,
那么这个数就叫a的立方根。
有两个平方根,
互为相反数
有一个平方根,是0
没有平方根
求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。
,其中a
是被开方数,
2是根指数(省略)
求一个数的立方根的运算
叫开立方;开立方与立方
是互逆运算。
有一个立方根,也是负数
有一个立方根,是0
有一个立方根,也是正数
,其中a
是被开方数,
3是根指数(不能省略)
讨论:你能归纳出平方根和立方根的异同点吗?
课堂小结:
1、立方根和开立方的定义.
2、正数、0、负数的立方根的特征.
3、立方根与平方根的异同.
4、你还有什么疑惑?
作业布置:
P52
习题6.2
第3,5题
