2020-2021学年苏科版八年级数学下册教学课件-9.5 三角形的中位线(17张PPT)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学下册教学课件-9.5 三角形的中位线(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 184.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
9.5
三角形的中位线
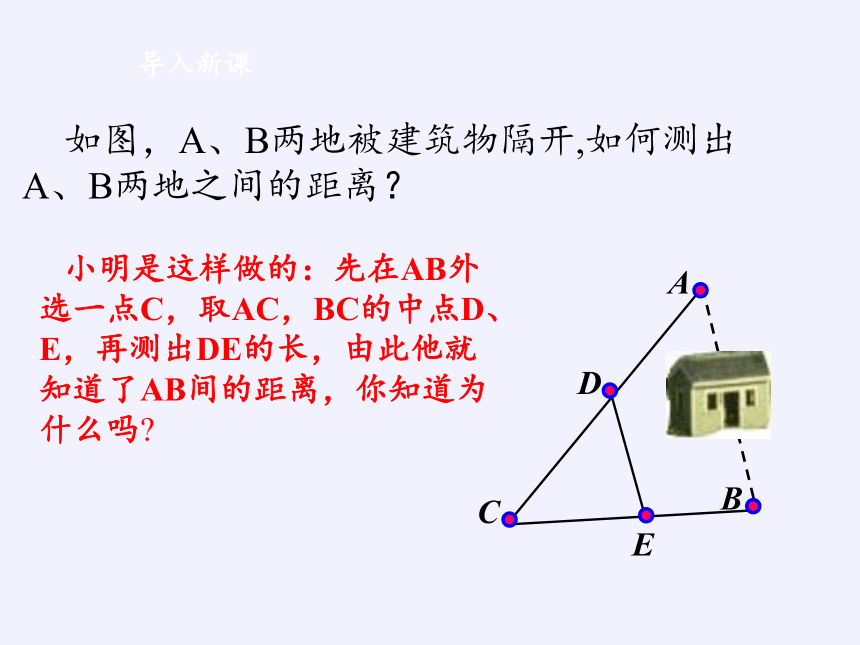
小明是这样做的:先在AB外选一点C,取AC,BC的中点D、E,再测出DE的长,由此他就知道了AB间的距离,你知道为什么吗?
如图,A、B两地被建筑物隔开,如何测出A、B两地之间的距离?
A
B
C
D
E
导入新课
导入新课
学习目标:
1.理解三角形中位线的概念,掌握三角形中位线定
理的内容;
2.经历探索,猜想,证明三角形的中位线定理的过
程,进一步发展推理论证的能力.
?
学习重点:
探索并证明三角形中位线定理.
学生自学
要求:
认真研读课本86-87页,思考下列问题:
1、三角形中线的概念,在练习本上画出一个三
角形,并画出它的中线。
2、三角形中位线的概念,在练习本上画出一个三角形,并画出它的中位线。
3、三角形中线与中位线有什么区别?
4、三角形的中位线有什么性质?
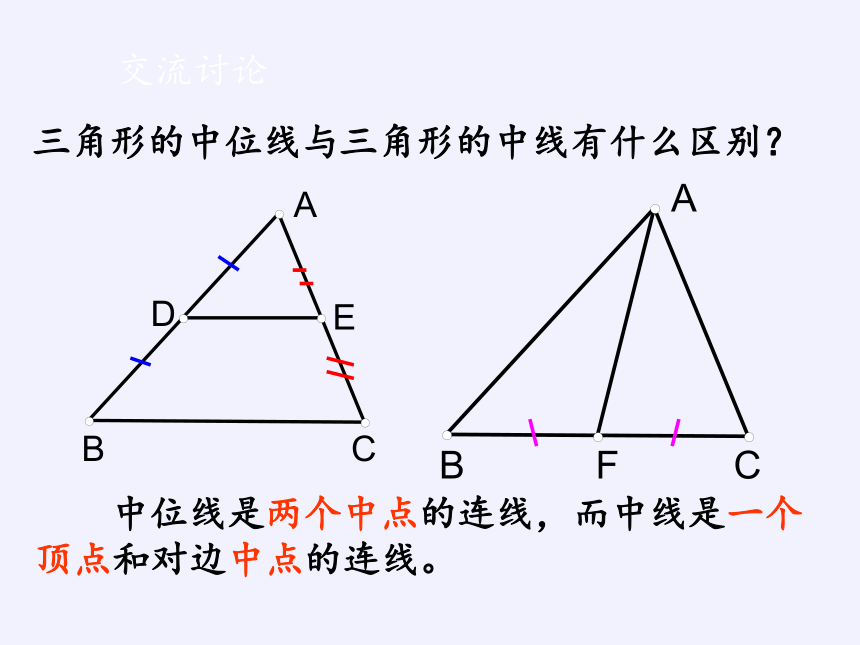
三角形的中位线与三角形的中线有什么区别?
中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。
交流讨论
观察下图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
猜想:DE∥BC
,DE=
BC
交流讨论
A
D
B
C
E
如何证明?
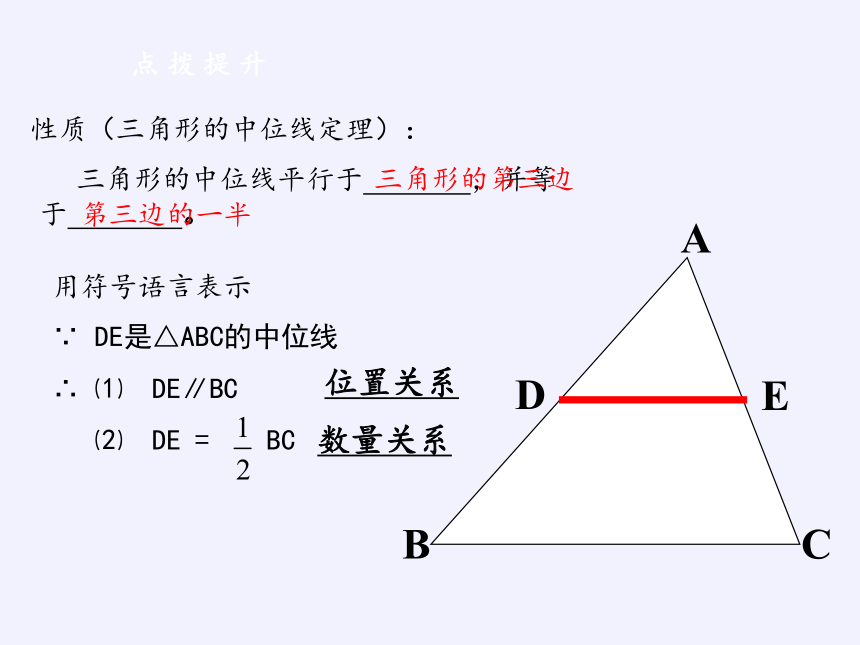
三角形的中位线平行于
,并等于
。
数量关系
位置关系
用符号语言表示
E
A
B
C
D
性质(三角形的中位线定理):
点
拨
提
升
三角形的第三边
第三边的一半
∵
DE是△ABC的中位线
∴
⑴
DE∥BC
⑵
DE
=
BC
小明是这样做的:先在AB外选一点C,取AC,BC的中点D、E,再测出DE的长,由此他就知道了AB间的距离,你知道为什么吗
?若DE的长为36m,AB=
。
1、如图,A、B两地被建筑物隔开,如何测出A、B两地之间的距离?
A
B
C
D
E
师友练习
72m
2、△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
A
E
D
C
B
(2)
B
D
A
E
C
(3)
3、△ABC中,D、E分别是AB、AC的中点,∠A=50°,
∠B=70°,则∠AED=_____.
师友练习
4、如图,在△ABC
中,D、E、F分别为边AB、BC、CA的中点。
证明:四边形DECF是平行四边形。
A
B
C
D
E
F
师友练习
5、已知:E、F、G、H分别是四边形ABCD中
AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
任意四边形四边中点连线所得的四边形一定是平行四边形。
总结梳理
要求:对照目标总结,通过本节课的学习
(1)本节课你学习了什么定理?
(2)定理的内容是什么?
(3)你是怎样得到定理的?
(4)应用定理可以解决数学中的哪些问题?
学习目标:
1.理解三角形中位线的概念,掌握三角形中位线定
理的内容;
2.经历探索,猜想,证明三角形的中位线定理的过
程,进一步发展推理论证的能力.
?
四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,则中点四边形EFGH是平行四边形.
A
C
E
D
H
F
G
点拨提升
1.若AC=BD,则
EFGH是
2.若AC⊥BD,则
EFGH是
B
3.若AC=BD且
AC⊥BD,
则
EFGH是
菱形
矩形
正方形
1.三角形的中位线定义.
2.三角形的中位线定理.
3.中位线定理为证明平行关系提供了新的方法;
中位线定理为证明一条线段是另一条线段的2倍或
1/2提供了一个新的途径。
总结梳理
拓展延伸
1、一个三角形的周长为12cm,则连接这个三角形各边中点形成三角形的周长为
。
2、如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB=2m,AB是△ABC的中位线,则CD=
。
3、已知等腰三角形两条中位线的长分别为3和5,则此等腰三角形的周长为
。
P
D
A
B
C
6cm
4m
26或22
拓展延伸
选做题:(学有余力的学生完成)
4、在如图△ABC中,DE是△ABC的中位线,AF是BC边上的中线.
AF、DE互相平分吗?
A
E
C
F
B
D
谢
谢
9.5
三角形的中位线
小明是这样做的:先在AB外选一点C,取AC,BC的中点D、E,再测出DE的长,由此他就知道了AB间的距离,你知道为什么吗?
如图,A、B两地被建筑物隔开,如何测出A、B两地之间的距离?
A
B
C
D
E
导入新课
导入新课
学习目标:
1.理解三角形中位线的概念,掌握三角形中位线定
理的内容;
2.经历探索,猜想,证明三角形的中位线定理的过
程,进一步发展推理论证的能力.
?
学习重点:
探索并证明三角形中位线定理.
学生自学
要求:
认真研读课本86-87页,思考下列问题:
1、三角形中线的概念,在练习本上画出一个三
角形,并画出它的中线。
2、三角形中位线的概念,在练习本上画出一个三角形,并画出它的中位线。
3、三角形中线与中位线有什么区别?
4、三角形的中位线有什么性质?
三角形的中位线与三角形的中线有什么区别?
中位线是两个中点的连线,而中线是一个顶点和对边中点的连线。
交流讨论
观察下图,你能发现△ABC的中位线DE与边BC的位置关系吗?度量一下,DE与BC之间有什么数量关系?
猜想:DE∥BC
,DE=
BC
交流讨论
A
D
B
C
E
如何证明?
三角形的中位线平行于
,并等于
。
数量关系
位置关系
用符号语言表示
E
A
B
C
D
性质(三角形的中位线定理):
点
拨
提
升
三角形的第三边
第三边的一半
∵
DE是△ABC的中位线
∴
⑴
DE∥BC
⑵
DE
=
BC
小明是这样做的:先在AB外选一点C,取AC,BC的中点D、E,再测出DE的长,由此他就知道了AB间的距离,你知道为什么吗
?若DE的长为36m,AB=
。
1、如图,A、B两地被建筑物隔开,如何测出A、B两地之间的距离?
A
B
C
D
E
师友练习
72m
2、△ABC中,D、E分别是AB、AC的中点,
BC=10cm,则DE=______.
A
E
D
C
B
(2)
B
D
A
E
C
(3)
3、△ABC中,D、E分别是AB、AC的中点,∠A=50°,
∠B=70°,则∠AED=_____.
师友练习
4、如图,在△ABC
中,D、E、F分别为边AB、BC、CA的中点。
证明:四边形DECF是平行四边形。
A
B
C
D
E
F
师友练习
5、已知:E、F、G、H分别是四边形ABCD中
AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。
任意四边形四边中点连线所得的四边形一定是平行四边形。
总结梳理
要求:对照目标总结,通过本节课的学习
(1)本节课你学习了什么定理?
(2)定理的内容是什么?
(3)你是怎样得到定理的?
(4)应用定理可以解决数学中的哪些问题?
学习目标:
1.理解三角形中位线的概念,掌握三角形中位线定
理的内容;
2.经历探索,猜想,证明三角形的中位线定理的过
程,进一步发展推理论证的能力.
?
四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,则中点四边形EFGH是平行四边形.
A
C
E
D
H
F
G
点拨提升
1.若AC=BD,则
EFGH是
2.若AC⊥BD,则
EFGH是
B
3.若AC=BD且
AC⊥BD,
则
EFGH是
菱形
矩形
正方形
1.三角形的中位线定义.
2.三角形的中位线定理.
3.中位线定理为证明平行关系提供了新的方法;
中位线定理为证明一条线段是另一条线段的2倍或
1/2提供了一个新的途径。
总结梳理
拓展延伸
1、一个三角形的周长为12cm,则连接这个三角形各边中点形成三角形的周长为
。
2、如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB=2m,AB是△ABC的中位线,则CD=
。
3、已知等腰三角形两条中位线的长分别为3和5,则此等腰三角形的周长为
。
P
D
A
B
C
6cm
4m
26或22
拓展延伸
选做题:(学有余力的学生完成)
4、在如图△ABC中,DE是△ABC的中位线,AF是BC边上的中线.
AF、DE互相平分吗?
A
E
C
F
B
D
谢
谢
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
