人教版七年级数学下册阶段复习·平行线的判定与性质的综合运用(19张ppt)
文档属性
| 名称 | 人教版七年级数学下册阶段复习·平行线的判定与性质的综合运用(19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览




文档简介
第五章 相交线与平行线
阶段复习——平行线的判定与性质的综合运用
知识点 平行线的判定与性质的综合运用
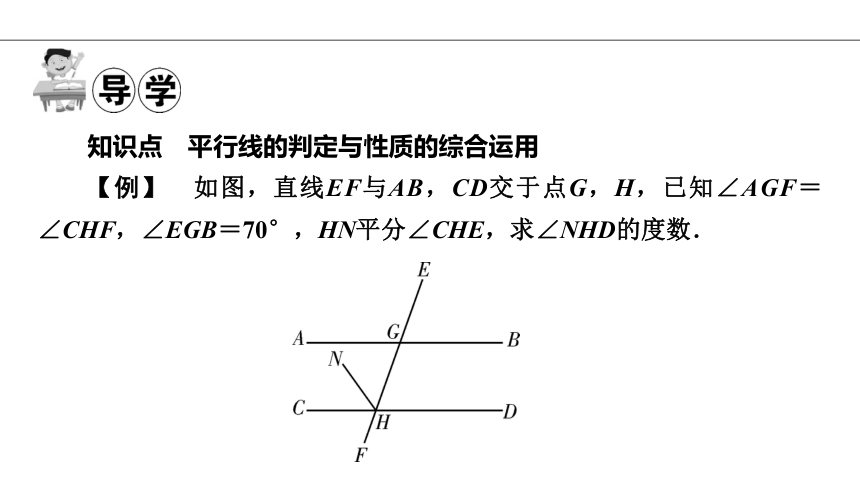
【例】 如图,直线EF与AB,CD交于点G,H,已知∠AGF=∠CHF,∠EGB=70°,HN平分∠CHE,求∠NHD的度数.
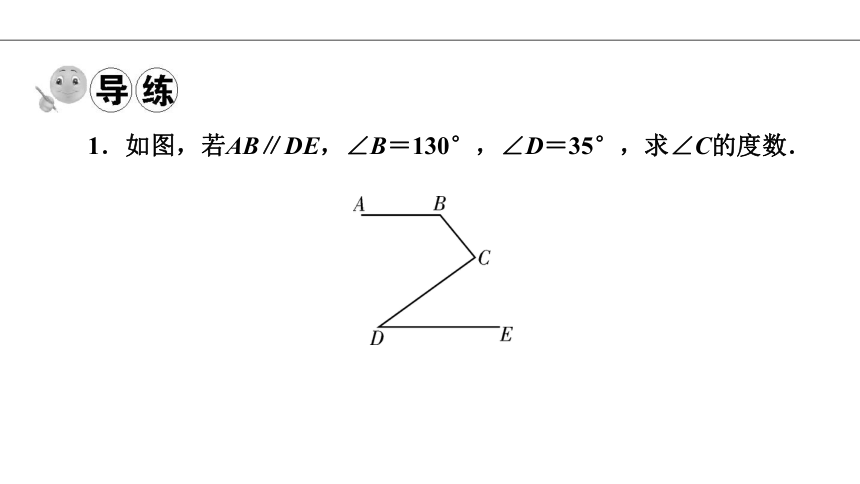
1.如图,若AB∥DE,∠B=130°,∠D=35°,求∠C的度数.
解:过C作CM∥AB,如图所示.
∵AB∥DE,
∴AB∥CM∥DE.
∴∠1+∠B=180°,∠2=∠D=35°.
∵∠B=130°,
∴∠1=180°-∠B=180°-130°=50°.
∴∠BCD=∠1+∠2=50°+35°=85°.
方法点拨:本题可运用“逆推”的方法求解,即从求解的结论逆推到已知条件,即求∠NHD→需求∠NHC→需求∠CHG→需求∠AGF,其中利用“同位角相等,两直线平行”得到AB∥CD,是本题求解的关键.
【第一关】 建议用时8分钟
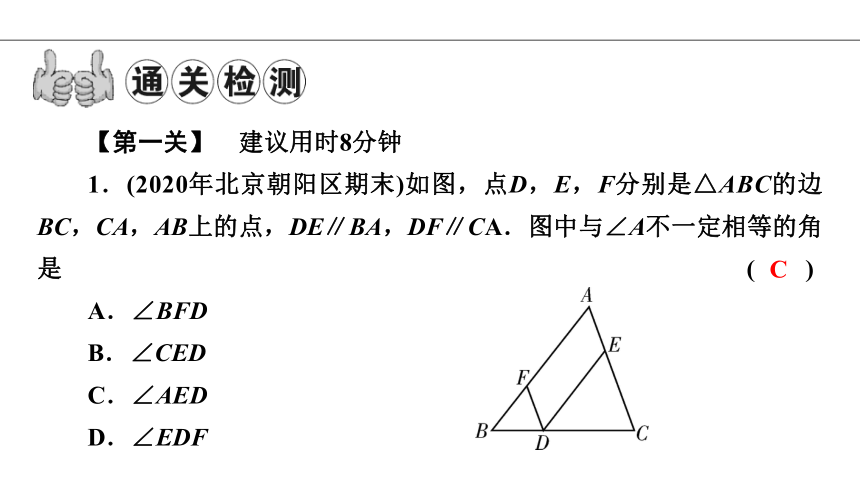
1.(2020年北京朝阳区期末)如图,点D,E,F分别是△ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.图中与∠A不一定相等的角是 ( )
A.∠BFD
B.∠CED
C.∠AED
D.∠EDF
C
2.(2020年杭州江干区期末)如图,CD平分∠ACB,DE∥AC,若∠ACD=35°,则∠DEB的度数为 ( )
?
?
?
A.35° B.55°
C.70° D.75°
C
3.(2020年益阳)如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为_________.
132°
4.(2020年广州白云区期末)如图,若AB∥CD∥EF,则∠BAC+∠ACE+∠CEF的度数为_________.
360°
5.如图,∠1=∠ACD,CE平分∠ACD,若∠CAE=110°,求∠AEC的度数.
解:∵∠1=∠ACD,∴AB∥CD.∴∠AEC=∠DCE,∠CAE+∠ACD=180°.
∴∠ACD=180°-∠CAE=180°-110°=70°.
∵CE平分∠ACD,∴∠ACE=∠DCE=35°.
∴∠AEC=∠DCE=35°.
6.(2020年中山期末)如图,已知∠1+∠2=180°,∠A=∠C,那么AF∥CE,为什么??
解:∵∠1=∠CMN,∠1+∠2=180°,
∴∠2+∠CMN=180°.
∴AB∥CD(同旁内角互补,两直线平行).
∴∠A=∠FDC(两直线平行,同位角相等).
∵∠A=∠C,∴∠FDC=∠C.
∴AF∥CE(内错角相等,两直线平行).
【第二关】 建议用时6分钟
7.(2020年合肥一模)如图,直线AB∥CD,AG平分∠BAE,∠EFC=40°,则∠GAF的度数为 ( )
A.110°
B.115°
C.125°
D.130°
A
【解析】∵AB∥CD,∠EFC=40°,
∴∠BAF=40°,∴∠BAE=140°,
又∵AG平分∠BAF,
∴∠BAG=70°,
∴∠GAF=70°+40°=110°.
8.阅读下面的推理过程,在括号内填上推理的依据,如图:
∵∠1+∠2=180°,∠2+∠4=180°(已知),
∴∠1=∠4(__________________).
∴a∥c(__________________________).
又∵∠2+∠3=180°(已知),∠3=∠6(______________),
∴∠2+∠6=180°(____________).
∴a∥b(____________________________).
∴b∥c(__________________________________).
同角的补角相等
内错角相等,两直线平行
对顶角相等
等量代换
同旁内角互补,两直线平行
平行于同一条直线的两条直线平行
9.已知直线a∥b,一块直角三角板按图示位置放置,已知∠1=37°,求∠2的度数.
解:作直线AB∥a,如图所示.
∴AB∥a∥b.
∵AB∥a,∴∠1=∠3.
∵AB∥b,∴∠2=∠4,
∵∠3+∠4=90°,
∴∠1+∠2=90°.
∵∠1=37°,
∴∠2=90°-∠1=90°-37°=53°.
【第三关】 自主选做
10.(2020年锦州期末)已知,如图,AB∥CD,∠BCF=180°,BD平分∠ABC,CE平分∠DCF,∠ACE=90°,求证:AC⊥BD.
阶段复习——平行线的判定与性质的综合运用
知识点 平行线的判定与性质的综合运用
【例】 如图,直线EF与AB,CD交于点G,H,已知∠AGF=∠CHF,∠EGB=70°,HN平分∠CHE,求∠NHD的度数.
1.如图,若AB∥DE,∠B=130°,∠D=35°,求∠C的度数.
解:过C作CM∥AB,如图所示.
∵AB∥DE,
∴AB∥CM∥DE.
∴∠1+∠B=180°,∠2=∠D=35°.
∵∠B=130°,
∴∠1=180°-∠B=180°-130°=50°.
∴∠BCD=∠1+∠2=50°+35°=85°.
方法点拨:本题可运用“逆推”的方法求解,即从求解的结论逆推到已知条件,即求∠NHD→需求∠NHC→需求∠CHG→需求∠AGF,其中利用“同位角相等,两直线平行”得到AB∥CD,是本题求解的关键.
【第一关】 建议用时8分钟
1.(2020年北京朝阳区期末)如图,点D,E,F分别是△ABC的边BC,CA,AB上的点,DE∥BA,DF∥CA.图中与∠A不一定相等的角是 ( )
A.∠BFD
B.∠CED
C.∠AED
D.∠EDF
C
2.(2020年杭州江干区期末)如图,CD平分∠ACB,DE∥AC,若∠ACD=35°,则∠DEB的度数为 ( )
?
?
?
A.35° B.55°
C.70° D.75°
C
3.(2020年益阳)如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为_________.
132°
4.(2020年广州白云区期末)如图,若AB∥CD∥EF,则∠BAC+∠ACE+∠CEF的度数为_________.
360°
5.如图,∠1=∠ACD,CE平分∠ACD,若∠CAE=110°,求∠AEC的度数.
解:∵∠1=∠ACD,∴AB∥CD.∴∠AEC=∠DCE,∠CAE+∠ACD=180°.
∴∠ACD=180°-∠CAE=180°-110°=70°.
∵CE平分∠ACD,∴∠ACE=∠DCE=35°.
∴∠AEC=∠DCE=35°.
6.(2020年中山期末)如图,已知∠1+∠2=180°,∠A=∠C,那么AF∥CE,为什么??
解:∵∠1=∠CMN,∠1+∠2=180°,
∴∠2+∠CMN=180°.
∴AB∥CD(同旁内角互补,两直线平行).
∴∠A=∠FDC(两直线平行,同位角相等).
∵∠A=∠C,∴∠FDC=∠C.
∴AF∥CE(内错角相等,两直线平行).
【第二关】 建议用时6分钟
7.(2020年合肥一模)如图,直线AB∥CD,AG平分∠BAE,∠EFC=40°,则∠GAF的度数为 ( )
A.110°
B.115°
C.125°
D.130°
A
【解析】∵AB∥CD,∠EFC=40°,
∴∠BAF=40°,∴∠BAE=140°,
又∵AG平分∠BAF,
∴∠BAG=70°,
∴∠GAF=70°+40°=110°.
8.阅读下面的推理过程,在括号内填上推理的依据,如图:
∵∠1+∠2=180°,∠2+∠4=180°(已知),
∴∠1=∠4(__________________).
∴a∥c(__________________________).
又∵∠2+∠3=180°(已知),∠3=∠6(______________),
∴∠2+∠6=180°(____________).
∴a∥b(____________________________).
∴b∥c(__________________________________).
同角的补角相等
内错角相等,两直线平行
对顶角相等
等量代换
同旁内角互补,两直线平行
平行于同一条直线的两条直线平行
9.已知直线a∥b,一块直角三角板按图示位置放置,已知∠1=37°,求∠2的度数.
解:作直线AB∥a,如图所示.
∴AB∥a∥b.
∵AB∥a,∴∠1=∠3.
∵AB∥b,∴∠2=∠4,
∵∠3+∠4=90°,
∴∠1+∠2=90°.
∵∠1=37°,
∴∠2=90°-∠1=90°-37°=53°.
【第三关】 自主选做
10.(2020年锦州期末)已知,如图,AB∥CD,∠BCF=180°,BD平分∠ABC,CE平分∠DCF,∠ACE=90°,求证:AC⊥BD.
