配方法电子稿
图片预览

文档简介
降次——解一元二次方程§22.2.1配方法
教学目标
了解配方法的概念,掌握运用配方法解一元二次方程的步骤.
重难点关键
1.重点:讲清配方法的解题步骤.
2.难点与关键:把常数项移到方程右边后,两边加上的常数是一次项系数一半的平方.
复习旧知
你学过的整式方程有哪些?它们是如何求解?
新知探索
问题1一桶某种油漆可刷的面积为1500dm2,李明用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,你能算出盒子的棱长吗?
对照上面的解方程的过程,你认为应怎样解方程x2+6x+9=2呢
方程x2+6x+9=2的左边是完全平方形式,这个方程可以化成(x+3)2=2,进行降次,得______________,方程的根为
x1=___________, x2=__________.
归纳反思:
如果方程能化成
的形式,那么等式两边直接开平方可得
尝试练习:
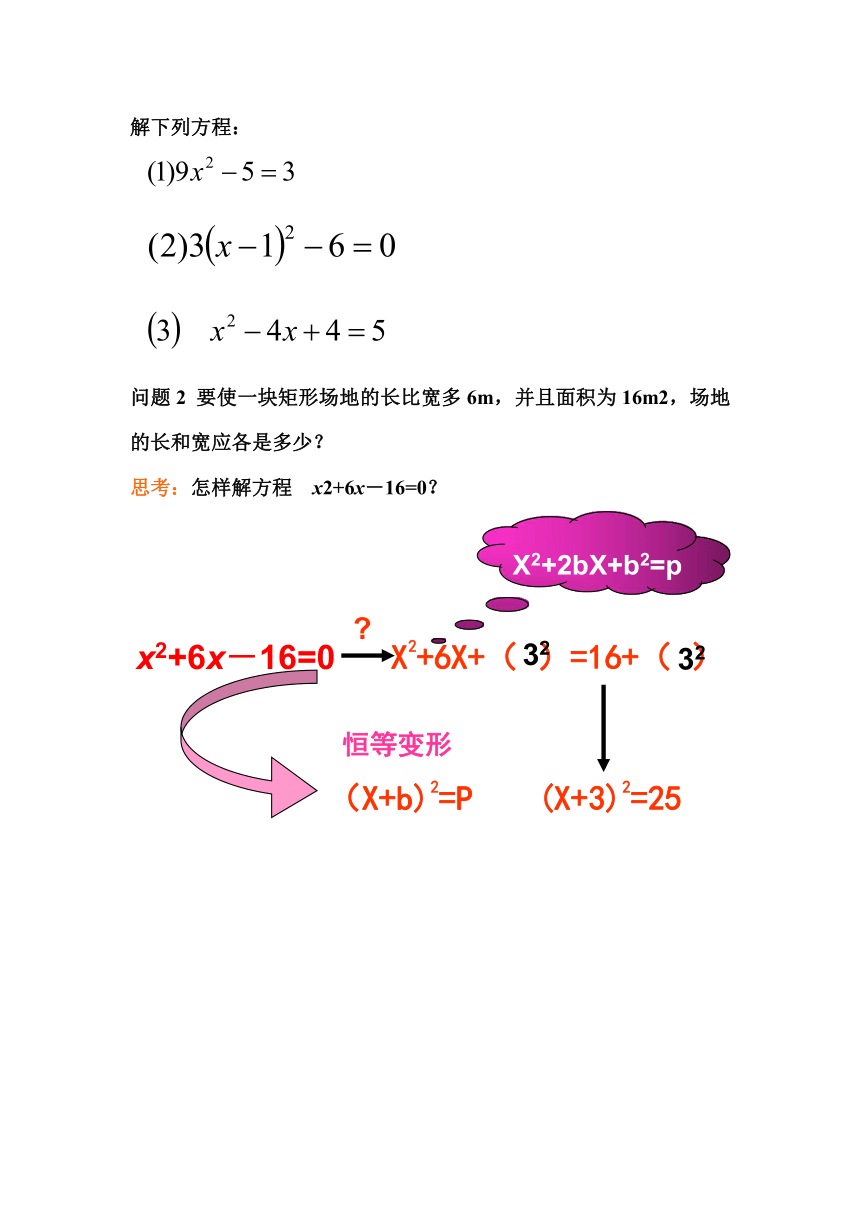
解下列方程:
问题2 要使一块矩形场地的长比宽多6m,并且面积为16m2,场地的长和宽应各是多少?
思考:怎样解方程 x2+6x-16=0?
经检验:2和-8是方程的两根,但是场地的宽不能是负值,所以场地的宽为2m,长为8m。
注意:实际问题一定要考虑解是否确实是实际问题的解(即解的合理性)。
讨论:以上解法中,为什么在方程x2+6x=16两边加9?加其他数行吗?
根据完全平方公式:9是一次项系数6一半的平方,加9正好于x2+6x能够配成一个完全平方式: x2 + 6x + 9= ( x + 3 )2
加其它数不行!
新知明晰:
配方法:通过配成完全平方形式来解一元二次方程的方法。
可以看出,配方是为了降次,把一个一元二次方程转化成两个一元一次方程来解.
例题讲解 提炼方法
例1 解下列方程:
方程的二次项系数不是1时,为便于配方,可以让方程的各项除以二次项系数.
忠告:如果最终结果想由“和或差的形式”写成“商的形式”请注意符号的问题。
提炼与升华
1、解一元二次方程的基本思路是什么?体现了什么数学思想?
2、解方程时变形的依据是什么?
3、用配方法解一元二次方程基本步骤是什么?
4、用配方法解一元二次方程应注意?
①应按步骤操作解题;
②不要忘记在等式的两边同时加一次项系数的一半的平方;
③开平方时若结果是二次根式要化简;
④如果最终结果想由“和或差的形式”写成“商的形式”,符号问题要当心.
x2+6x-16=0
(X+b)2=P
X2+6X+( )=16+( )
X2+2bX+b2=p
(X+3)2=25
32
32
恒等变形
x2+6x-16=0
x2+6x=16
x2+6x+9=16+9
( x + 3 )2=25
x+3=±5
x+3=5,x+3=-5
x1=2,x2=-8
降次求解的思路流程
移项
左边写成平方形式
直接开平方降次
两边加9(即
)
左边配成 x2+2bx+b2
解一次方程
当一元二次方程化为一般形式后,配方降次的一般步骤是:
二次项的系数
=1
≠1
(两边同除以二次项的系数)
二次项的系数化成1
移项
配方
(移常数项到等号右边)
(等式两边同加一次项系数一半的平方)
化成一次方程
(两边直接开平方)
5、你还有什么疑惑?
教学目标
了解配方法的概念,掌握运用配方法解一元二次方程的步骤.
重难点关键
1.重点:讲清配方法的解题步骤.
2.难点与关键:把常数项移到方程右边后,两边加上的常数是一次项系数一半的平方.
复习旧知
你学过的整式方程有哪些?它们是如何求解?
新知探索
问题1一桶某种油漆可刷的面积为1500dm2,李明用这桶油漆恰好刷完10个同样的正方体形状的盒子的全部外表面,你能算出盒子的棱长吗?
对照上面的解方程的过程,你认为应怎样解方程x2+6x+9=2呢
方程x2+6x+9=2的左边是完全平方形式,这个方程可以化成(x+3)2=2,进行降次,得______________,方程的根为
x1=___________, x2=__________.
归纳反思:
如果方程能化成
的形式,那么等式两边直接开平方可得
尝试练习:
解下列方程:
问题2 要使一块矩形场地的长比宽多6m,并且面积为16m2,场地的长和宽应各是多少?
思考:怎样解方程 x2+6x-16=0?
经检验:2和-8是方程的两根,但是场地的宽不能是负值,所以场地的宽为2m,长为8m。
注意:实际问题一定要考虑解是否确实是实际问题的解(即解的合理性)。
讨论:以上解法中,为什么在方程x2+6x=16两边加9?加其他数行吗?
根据完全平方公式:9是一次项系数6一半的平方,加9正好于x2+6x能够配成一个完全平方式: x2 + 6x + 9= ( x + 3 )2
加其它数不行!
新知明晰:
配方法:通过配成完全平方形式来解一元二次方程的方法。
可以看出,配方是为了降次,把一个一元二次方程转化成两个一元一次方程来解.
例题讲解 提炼方法
例1 解下列方程:
方程的二次项系数不是1时,为便于配方,可以让方程的各项除以二次项系数.
忠告:如果最终结果想由“和或差的形式”写成“商的形式”请注意符号的问题。
提炼与升华
1、解一元二次方程的基本思路是什么?体现了什么数学思想?
2、解方程时变形的依据是什么?
3、用配方法解一元二次方程基本步骤是什么?
4、用配方法解一元二次方程应注意?
①应按步骤操作解题;
②不要忘记在等式的两边同时加一次项系数的一半的平方;
③开平方时若结果是二次根式要化简;
④如果最终结果想由“和或差的形式”写成“商的形式”,符号问题要当心.
x2+6x-16=0
(X+b)2=P
X2+6X+( )=16+( )
X2+2bX+b2=p
(X+3)2=25
32
32
恒等变形
x2+6x-16=0
x2+6x=16
x2+6x+9=16+9
( x + 3 )2=25
x+3=±5
x+3=5,x+3=-5
x1=2,x2=-8
降次求解的思路流程
移项
左边写成平方形式
直接开平方降次
两边加9(即
)
左边配成 x2+2bx+b2
解一次方程
当一元二次方程化为一般形式后,配方降次的一般步骤是:
二次项的系数
=1
≠1
(两边同除以二次项的系数)
二次项的系数化成1
移项
配方
(移常数项到等号右边)
(等式两边同加一次项系数一半的平方)
化成一次方程
(两边直接开平方)
5、你还有什么疑惑?
同课章节目录
