6.3万有引力定律—2020-2021学年人教版高中物理必修二课件24张PPT
文档属性
| 名称 | 6.3万有引力定律—2020-2021学年人教版高中物理必修二课件24张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-18 23:52:07 | ||
图片预览








文档简介
6.3万有引力定律
人教版 高中物理必修二
第六章万有引力与航天
一、月——地检验
牛顿的思考
通过上一节课的学习,我们已经知道太阳与行星间的引力大小可以用公式F=GMm/r2计算。
然而上式的推导是立足于开普勒定律,因此该公式仅对“行星绕太阳运动”成立,这还不是万有引力定律。那牛顿又是怎样向前迈出的一大步呢?他的思想是怎样超越了行星与太阳呢?
一、月——地检验
通过前面的分析,我们已经推导出引力公式是可以很好解释行星绕太阳转动的问题。但是牛顿不甘心以此,他接着设想:太阳与行星间的引力使得行星不能飞离太阳;那距离地球很高的月球不停的绕地球转动而没有飞离地球,是不是也是由于地球对月球的引力作用?如果是,那这两个引力是否为同一种力?
而如果将距离地球的距离不断减少,我们能
发现地面上的很多物体(如苹果),被抛出
后都要落回底面,这又是什么力使得苹果离
不开地球呢?是否也是由于地球对苹果的引
力造成的?那地球对苹果的引力和太阳对行
星的引力是否根本上就是同一种力?
结论普遍性的猜想与假设
一、月——地检验
开普勒行星运动定律揭示了行星的运动规律,回答了人们千百年来一直追寻的 “行星怎样运动”的问题。然而好奇的人们,却并不满足,他们面向天穹,深情地叩问:行星为什么要这样运动?是什么力量支配着行星绕着太阳做如此和谐而有规律的运动呢?
历史上人们关于行星运动原因的猜想与假设
牛顿的思考
一、月——地检验
1.行星绕太阳运动,太阳对行星的引力提供向心力。月球绕地球运动,地球对月球的引力提供向心力。如果地球对月球的引力跟太阳对行星的引力性质相同,那么地球对月球的引力的表达式是什么?
2.如何推导月球绕地球的向心加速度表达式?
检验与论证
一、月——地检验
检验与论证
3.假设苹果受到地球的引力也与月球受到地球的引力性质相同,那么苹果做自由落体运动的加速度表达式是什么?如何验证苹果受到地球的引力与月球受到地球的引力性质相同呢?已知月球到地球的距离r约为地球半径R的60倍。
二、万有引力定律
这表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律。
1.定律内容:自然界中________两个物体都是相互吸引的,引力的大小跟这两个物体的______________成正比,跟它们的距离的__________成反比。
2.表达式:F=_________
式中,质量的单位用______,距离的单位用_____,力的单位用_____,G称为__________,适用于任何两个物体,单位为___________。
任何
质量的乘积
二次方
kg
m
N
引力常量
Nm2/kg2
二、万有引力定律
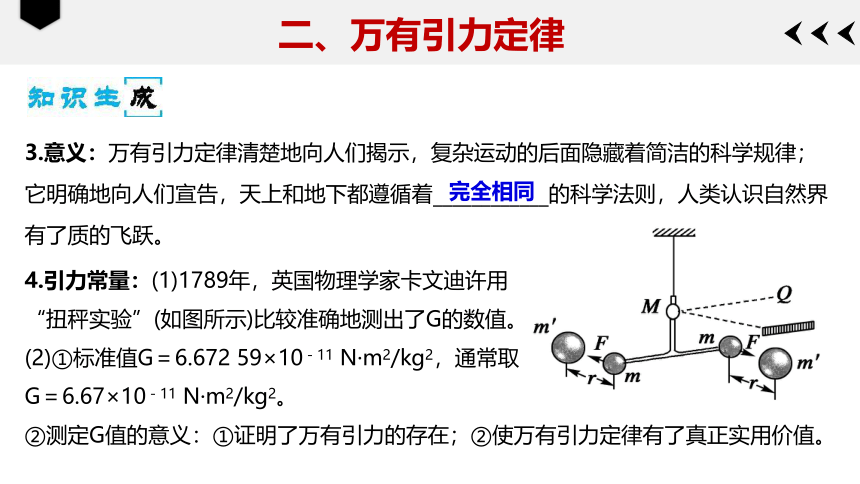
3.意义:万有引力定律清楚地向人们揭示,复杂运动的后面隐藏着简洁的科学规律;它明确地向人们宣告,天上和地下都遵循着____________的科学法则,人类认识自然界有了质的飞跃。
完全相同
4.引力常量:(1)1789年,英国物理学家卡文迪许用
“扭秤实验”(如图所示)比较准确地测出了G的数值。
(2)①标准值G=6.672 59×10-11 N·m2/kg2,通常取
G=6.67×10-11 N·m2/kg2。
②测定G值的意义:①证明了万有引力的存在;②使万有引力定律有了真正实用价值。
二、万有引力定律
对于万有引力定律的表达式F= ,下面说法中正确的是( )
A.当r趋近于零时,万有引力趋于无穷大
B.公式中G为引力常量,它是由实验测得的,而不是人为规定的
C.若m1>m2,则m1受到的引力大于m2受到的引力
D.m1与m2受到的引力大小相等,是一对平衡力
B
二、万有引力定律
5.万有引力定律的四个特性
①普遍性:万有引力不仅存在于星球间,任何客观存在的有质量的物体之间都存在着这种相互吸引力。
②相互性:两个物体相互作用的引力是一对作用力和反作用力,它们大小相等,方向相反,分别作用在两个物体上。
③宏观性:在通常情况下万有引力非常小,只有在质量巨大的星球间或天体与天体附近的物体间,它的存在才有实际的物理意义,故在分析地球表面物体受力时,不考虑其他物体对它的万有引力。
④特殊性:两个物体间的万有引力只与它们本身的质量有关,与它们之间的距离有关。而与所在空间的性质无关。
二、万有引力定律
5.万有引力表达式F=Gm1m2/r2的适用条件
①严格地说,万有引力定律只适用于质点的相互作用,如果两个物体间的距离远远大于物体本身的大小时,物体可看成质点,公式可近似适用,其中r为两物体质心间的距离。
②两个质量分布均匀的球体或球壳间的相互作用,也可用万有引力定律计算,其中r是两个球体或球壳的球心间的距离。
③当物体不能看成质点时,可把物体假想分割成无数个质点或者质量分布的球体,求出每一个物体上每个质点与另一个物体上每个质点间的万有引力,然后求合力。
如图所示,两球间的距离为r0。两球的质量分布均匀,质量分别为m1、m2,半径分别为r1、r2,则两球间的万有引力大小为( )。
D
有一质量为M、半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的质点,现在从M中挖去一半径为R/2的球体,如图所示,求剩下部分对质点的万有引力F为多大?
?
万有引力公式F=GMm/r2仅适用于两个质点之间和质量分布均匀的球体或球壳之间(两球体的球心距离为r)。
计算一些非球形物体间的万有引力,常采用割补法。对本来是非对称的物体,通过割补后构成对称物体,然后再利用对称物体所满足的物理规律进行求解的方法称为割补法。
割补法求解万有引力
三、重力和万有引力的区别与联系
如图所示,把地球视为质量分布均匀的球体,人站在地球的不同位置,比如赤道、两极或者其他位置,请思考:
(1)人在地球的不同位置,受到的万有引力大小一样吗?
(2)人在地球的不同位置,受到的重力大小一样吗?
提示:(1)根据万有引力定律F=GMm/R2可知,人在地球的不同位置,受到的万有引力大小一样;
(2)重力是万有引力的一个分力,由于人随地球转动,还需要向心力,在地球的不同位置,向心力不同,所以人在地球的不同位置,受的重力大小不一样。
三、重力和万有引力的区别与联系
1.重力为地球引力的分力
如图所示,设地球的质量为M,半径为R,A处物体的质量为m,物体受到地球的吸引力为F,方向指向地心O,由万有引力公式得F=GMm/r2。引力F可分解为F1、F2两个分力,其中F1为物体随地球自转做圆周运动的向心力Fn,F2就是物体的重力mg。
三、重力和万有引力的区别与联系
2.重力与纬度的关系
地面上物体的重力随纬度的升高而变大。
(1)赤道上:重力和向心力在一条直线上F=Fn+mg,即GMm/R2=mRω2+mg,所以mg=GMm/R2-mRω2。
(2)地球两极处:向心力为零,所以mg0=F=GMm/R2。
(3)其他位置:重力是万有引力的一个分力,重力的大小mg三、重力和万有引力的区别与联系
2.重力与纬度的关系
地面上物体的重力随纬度的升高而变大。
(1)赤道上:重力和向心力在一条直线上F=Fn+mg,即GMm/R2=mRω2+mg,所以mg=GMm/R2-mRω2。
(2)地球两极处:向心力为零,所以mg0=F=GMm/R2。
(3)其他位置:重力是万有引力的一个分力,重力的大小mg三、重力和万有引力的区别与联系
3.重力与高度的关系
由于地球的自转角速度很小,故地球自转带来的影响很小,一般情况下认为在地面附近:mg=GMm/R2,若距离地面的高度为h,则mg=GMm/(R+h)2(R为地球半径,g为离地面h高度处的重力加速度)。所以距地面越高,物体的重力加速度越小,则物体所受的重力也越小。
特别提醒:(1)物体随地球自转需要的向心力很小,一般情况下,重力约等于万有引力,即mg=GMm/R2。 (2)在地球表面,重力加速度随地理纬度的升高而增大;在地球上空,重力加速度随距地面高度的增加而减小。
课后练习:
某个行星的质量是地球质量的一半,半径也是地球半径的一半。某运动员在地球上能举起250 kg的杠铃,在该行星上最多能举起质量为多少的杠铃?
课后作业:
完成第六章第三节相关练习
预习第六章第四节相关知识
人教版 高中物理必修二
第六章万有引力与航天
一、月——地检验
牛顿的思考
通过上一节课的学习,我们已经知道太阳与行星间的引力大小可以用公式F=GMm/r2计算。
然而上式的推导是立足于开普勒定律,因此该公式仅对“行星绕太阳运动”成立,这还不是万有引力定律。那牛顿又是怎样向前迈出的一大步呢?他的思想是怎样超越了行星与太阳呢?
一、月——地检验
通过前面的分析,我们已经推导出引力公式是可以很好解释行星绕太阳转动的问题。但是牛顿不甘心以此,他接着设想:太阳与行星间的引力使得行星不能飞离太阳;那距离地球很高的月球不停的绕地球转动而没有飞离地球,是不是也是由于地球对月球的引力作用?如果是,那这两个引力是否为同一种力?
而如果将距离地球的距离不断减少,我们能
发现地面上的很多物体(如苹果),被抛出
后都要落回底面,这又是什么力使得苹果离
不开地球呢?是否也是由于地球对苹果的引
力造成的?那地球对苹果的引力和太阳对行
星的引力是否根本上就是同一种力?
结论普遍性的猜想与假设
一、月——地检验
开普勒行星运动定律揭示了行星的运动规律,回答了人们千百年来一直追寻的 “行星怎样运动”的问题。然而好奇的人们,却并不满足,他们面向天穹,深情地叩问:行星为什么要这样运动?是什么力量支配着行星绕着太阳做如此和谐而有规律的运动呢?
历史上人们关于行星运动原因的猜想与假设
牛顿的思考
一、月——地检验
1.行星绕太阳运动,太阳对行星的引力提供向心力。月球绕地球运动,地球对月球的引力提供向心力。如果地球对月球的引力跟太阳对行星的引力性质相同,那么地球对月球的引力的表达式是什么?
2.如何推导月球绕地球的向心加速度表达式?
检验与论证
一、月——地检验
检验与论证
3.假设苹果受到地球的引力也与月球受到地球的引力性质相同,那么苹果做自由落体运动的加速度表达式是什么?如何验证苹果受到地球的引力与月球受到地球的引力性质相同呢?已知月球到地球的距离r约为地球半径R的60倍。
二、万有引力定律
这表明,地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,真的遵从相同的规律。
1.定律内容:自然界中________两个物体都是相互吸引的,引力的大小跟这两个物体的______________成正比,跟它们的距离的__________成反比。
2.表达式:F=_________
式中,质量的单位用______,距离的单位用_____,力的单位用_____,G称为__________,适用于任何两个物体,单位为___________。
任何
质量的乘积
二次方
kg
m
N
引力常量
Nm2/kg2
二、万有引力定律
3.意义:万有引力定律清楚地向人们揭示,复杂运动的后面隐藏着简洁的科学规律;它明确地向人们宣告,天上和地下都遵循着____________的科学法则,人类认识自然界有了质的飞跃。
完全相同
4.引力常量:(1)1789年,英国物理学家卡文迪许用
“扭秤实验”(如图所示)比较准确地测出了G的数值。
(2)①标准值G=6.672 59×10-11 N·m2/kg2,通常取
G=6.67×10-11 N·m2/kg2。
②测定G值的意义:①证明了万有引力的存在;②使万有引力定律有了真正实用价值。
二、万有引力定律
对于万有引力定律的表达式F= ,下面说法中正确的是( )
A.当r趋近于零时,万有引力趋于无穷大
B.公式中G为引力常量,它是由实验测得的,而不是人为规定的
C.若m1>m2,则m1受到的引力大于m2受到的引力
D.m1与m2受到的引力大小相等,是一对平衡力
B
二、万有引力定律
5.万有引力定律的四个特性
①普遍性:万有引力不仅存在于星球间,任何客观存在的有质量的物体之间都存在着这种相互吸引力。
②相互性:两个物体相互作用的引力是一对作用力和反作用力,它们大小相等,方向相反,分别作用在两个物体上。
③宏观性:在通常情况下万有引力非常小,只有在质量巨大的星球间或天体与天体附近的物体间,它的存在才有实际的物理意义,故在分析地球表面物体受力时,不考虑其他物体对它的万有引力。
④特殊性:两个物体间的万有引力只与它们本身的质量有关,与它们之间的距离有关。而与所在空间的性质无关。
二、万有引力定律
5.万有引力表达式F=Gm1m2/r2的适用条件
①严格地说,万有引力定律只适用于质点的相互作用,如果两个物体间的距离远远大于物体本身的大小时,物体可看成质点,公式可近似适用,其中r为两物体质心间的距离。
②两个质量分布均匀的球体或球壳间的相互作用,也可用万有引力定律计算,其中r是两个球体或球壳的球心间的距离。
③当物体不能看成质点时,可把物体假想分割成无数个质点或者质量分布的球体,求出每一个物体上每个质点与另一个物体上每个质点间的万有引力,然后求合力。
如图所示,两球间的距离为r0。两球的质量分布均匀,质量分别为m1、m2,半径分别为r1、r2,则两球间的万有引力大小为( )。
D
有一质量为M、半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的质点,现在从M中挖去一半径为R/2的球体,如图所示,求剩下部分对质点的万有引力F为多大?
?
万有引力公式F=GMm/r2仅适用于两个质点之间和质量分布均匀的球体或球壳之间(两球体的球心距离为r)。
计算一些非球形物体间的万有引力,常采用割补法。对本来是非对称的物体,通过割补后构成对称物体,然后再利用对称物体所满足的物理规律进行求解的方法称为割补法。
割补法求解万有引力
三、重力和万有引力的区别与联系
如图所示,把地球视为质量分布均匀的球体,人站在地球的不同位置,比如赤道、两极或者其他位置,请思考:
(1)人在地球的不同位置,受到的万有引力大小一样吗?
(2)人在地球的不同位置,受到的重力大小一样吗?
提示:(1)根据万有引力定律F=GMm/R2可知,人在地球的不同位置,受到的万有引力大小一样;
(2)重力是万有引力的一个分力,由于人随地球转动,还需要向心力,在地球的不同位置,向心力不同,所以人在地球的不同位置,受的重力大小不一样。
三、重力和万有引力的区别与联系
1.重力为地球引力的分力
如图所示,设地球的质量为M,半径为R,A处物体的质量为m,物体受到地球的吸引力为F,方向指向地心O,由万有引力公式得F=GMm/r2。引力F可分解为F1、F2两个分力,其中F1为物体随地球自转做圆周运动的向心力Fn,F2就是物体的重力mg。
三、重力和万有引力的区别与联系
2.重力与纬度的关系
地面上物体的重力随纬度的升高而变大。
(1)赤道上:重力和向心力在一条直线上F=Fn+mg,即GMm/R2=mRω2+mg,所以mg=GMm/R2-mRω2。
(2)地球两极处:向心力为零,所以mg0=F=GMm/R2。
(3)其他位置:重力是万有引力的一个分力,重力的大小mg
2.重力与纬度的关系
地面上物体的重力随纬度的升高而变大。
(1)赤道上:重力和向心力在一条直线上F=Fn+mg,即GMm/R2=mRω2+mg,所以mg=GMm/R2-mRω2。
(2)地球两极处:向心力为零,所以mg0=F=GMm/R2。
(3)其他位置:重力是万有引力的一个分力,重力的大小mg
3.重力与高度的关系
由于地球的自转角速度很小,故地球自转带来的影响很小,一般情况下认为在地面附近:mg=GMm/R2,若距离地面的高度为h,则mg=GMm/(R+h)2(R为地球半径,g为离地面h高度处的重力加速度)。所以距地面越高,物体的重力加速度越小,则物体所受的重力也越小。
特别提醒:(1)物体随地球自转需要的向心力很小,一般情况下,重力约等于万有引力,即mg=GMm/R2。 (2)在地球表面,重力加速度随地理纬度的升高而增大;在地球上空,重力加速度随距地面高度的增加而减小。
课后练习:
某个行星的质量是地球质量的一半,半径也是地球半径的一半。某运动员在地球上能举起250 kg的杠铃,在该行星上最多能举起质量为多少的杠铃?
课后作业:
完成第六章第三节相关练习
预习第六章第四节相关知识
