5.1曲线运动(关联速度问题)—人教版高中物理必修二课件16张PPT
文档属性
| 名称 | 5.1曲线运动(关联速度问题)—人教版高中物理必修二课件16张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 497.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-19 00:24:14 | ||
图片预览




文档简介
5.1 曲线运动
(关联速度问题)
人教版 高中物理必修二
第五章曲线运动
一、关联速度问题
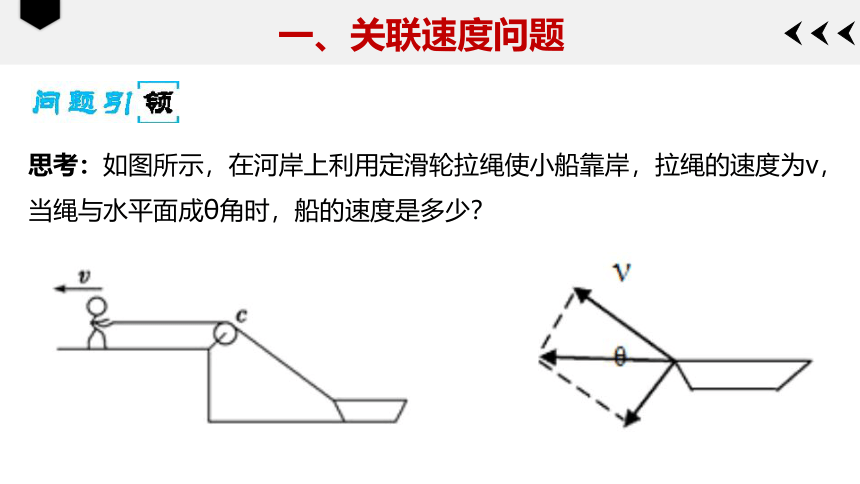
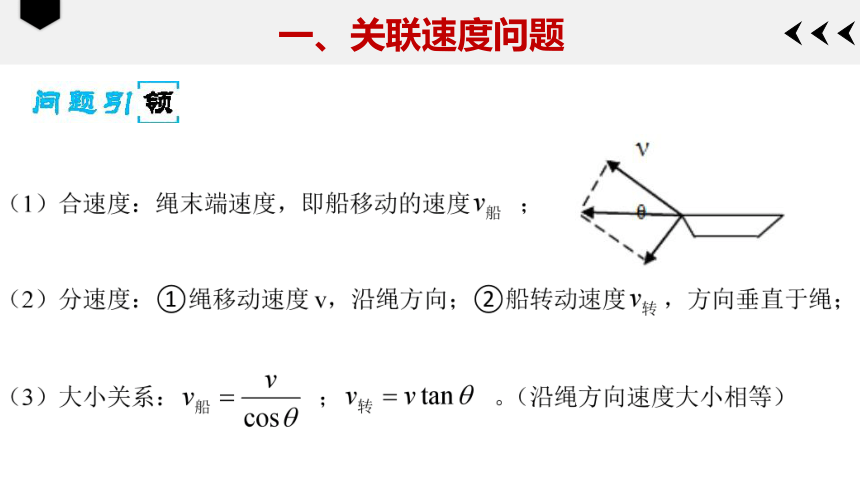
思考:如图所示,在河岸上利用定滑轮拉绳使小船靠岸,拉绳的速度为v,当绳与水平面成θ角时,船的速度是多少?
一、关联速度问题
一、关联速度问题
模型展示:船在靠岸的过程中,通过一条跨过定滑轮的绳拉船.研究拉船的绳端速度与船速的关系.在绳跟滑轮间的支撑点看绳拉船头部位,该部位的实际运动是受水面约束的直线运动,这也是合运动.
它实际上是同时参与了两个分运动:一是沿绳方向的直线运动;二是具有沿垂直绳方向线速度的圆周运动.
此类问题在建筑工地的塔吊工作中也很常见.
一、关联速度问题
1.常见关联速度模型:用轻绳、轻杆连接的物体或相互接触的物体间的关联速度。
一、关联速度问题
2.关联速度问题特点:
(1)绳(杆)物关联问题:两物体通过绳(杆)相牵连,当两物体都发生运动时,两物体的速度往往不相等,但因绳(杆)的长度是不变的,因此两物体的速度沿绳(杆)方向的分速度大小是相等的。
(2)杆点(面)关联问题:杆的一端和一个物体的某点(面)接触,两物体通过绳(杆)相牵连,当两物体都发生运动时,两物体的速度往往不相等,但因二者始终接触,因此两物体的速度沿垂直接触面方向的分速度大小是相等的。
用绳连接的物体的“关联”问题:
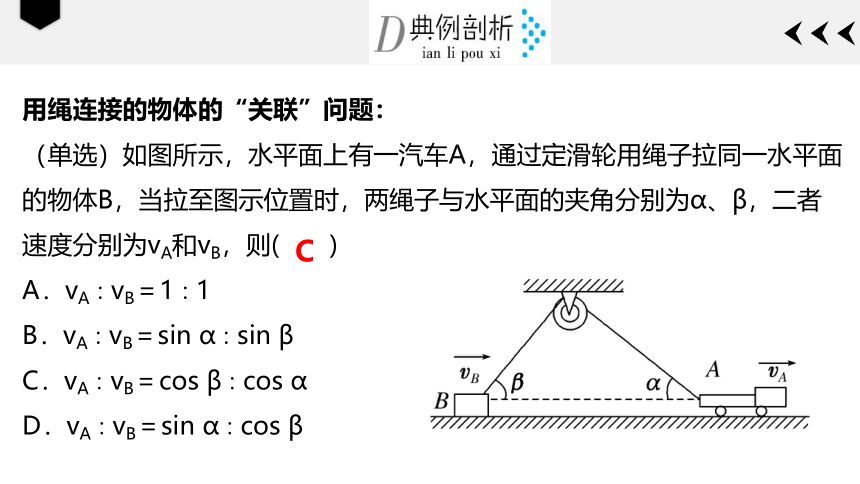
(单选)如图所示,水平面上有一汽车A,通过定滑轮用绳子拉同一水平面的物体B,当拉至图示位置时,两绳子与水平面的夹角分别为α、β,二者速度分别为vA和vB,则( )
A.vA∶vB=1∶1
B.vA∶vB=sin α∶sin β
C.vA∶vB=cos β∶cos α
D.vA∶vB=sin α∶cos β
C
用杆连接的物体的“关联”问题:
如图两根光滑的杆互相垂直地固定在一起,是国内棉分别穿有一个小球,小球a.b间用一细直棒相连。当细直棒与竖直杆夹角为? 时,求小球a.b实际速度大小之比。
【答案】Va/Vb=tanθ
相互接触的物体的“关联”问题:
如图所示,斜劈B的倾角为30°,劈尖顶着竖直墙壁静止于水平地面上,现将一半径为r的球A放在墙面与斜劈之间,并从图示位置由静止释放,不计一切摩擦,求某一时刻两物体的瞬时速度VA与VB的大小的比值?
一、关联速度问题
总结四个关键点:
①确定研究对象——绳、杆的端点或面接触点,分解的是速度方向不在绳、杆的方向上的物体(即v平行于绳,不分解;v不平行于绳,要分解);
②确定合运动(合速度)——实际的运动一定是合运动;
③确定分运动(分速度)——一般沿绳、杆的方向和垂直于绳、杆的方向;
④沿绳、杆或接触面间弹力方向的分速度相等。
一、关联速度问题
针对练习1:质量为m的物体P置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动.当小车与滑轮间的细绳和水平方向成夹角θ2时(如图),下列判断正确的是( )
A.P的速率为v
B.P的速率为vcosθ2
C.绳的拉力等于mgsinθ1
D.绳的拉力小于mgsinθ1
B
针对练习2:如图所示,一条细绳跨过定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直杆上,两物体均保持静止,不计绳与滑轮、B与竖直杆间的摩擦,已知绳与竖直杆间的夹角为θ,则物体A、B的质量之比mA:mB等于( )
A.cosθ:1
B.1:cosθ
C.tanθ:1
D.1:sinθ
B
针对练习3:如图所示,在光滑的水平地面上有一个表面光滑的立方体M,一轻杆L与水平地面成α角,轻杆的下端用光滑铰链连接于O点,O点固定于地面上,轻杆的上端连接着一个小球m,小球靠在立方体左侧,立方体右侧受到水平向左推力F的作用,整个装置处于静止状态.若现在撤去水平推力F,则下列说法中正确的是( )
A.在小球和立方体分离前,若小球的速度大小为v1,
立方体的速度大小为v2,则有v1=v2sinα
B.小球在落地的瞬间和立方体分离
C.小球和立方体分离时小球只受重力
D.立方体最终将做匀速直线运动
D
针对练习4:固定在竖直平面内的半圆形刚性铁环,半径为R,铁环上穿着小球,铁环圆心O的正上方固定一个小定滑轮。用一条不可伸长的细绳,通过定滑轮以一定速度拉着小球从A点开始沿铁环运动,某时刻角度关系如图所示,若绳末端速度为v,则小球此时的速度为( )
A. B. C. D.2v
A
课后作业:
完成第五章第一节相关练习
预习第五章第二节相关知识
(关联速度问题)
人教版 高中物理必修二
第五章曲线运动
一、关联速度问题
思考:如图所示,在河岸上利用定滑轮拉绳使小船靠岸,拉绳的速度为v,当绳与水平面成θ角时,船的速度是多少?
一、关联速度问题
一、关联速度问题
模型展示:船在靠岸的过程中,通过一条跨过定滑轮的绳拉船.研究拉船的绳端速度与船速的关系.在绳跟滑轮间的支撑点看绳拉船头部位,该部位的实际运动是受水面约束的直线运动,这也是合运动.
它实际上是同时参与了两个分运动:一是沿绳方向的直线运动;二是具有沿垂直绳方向线速度的圆周运动.
此类问题在建筑工地的塔吊工作中也很常见.
一、关联速度问题
1.常见关联速度模型:用轻绳、轻杆连接的物体或相互接触的物体间的关联速度。
一、关联速度问题
2.关联速度问题特点:
(1)绳(杆)物关联问题:两物体通过绳(杆)相牵连,当两物体都发生运动时,两物体的速度往往不相等,但因绳(杆)的长度是不变的,因此两物体的速度沿绳(杆)方向的分速度大小是相等的。
(2)杆点(面)关联问题:杆的一端和一个物体的某点(面)接触,两物体通过绳(杆)相牵连,当两物体都发生运动时,两物体的速度往往不相等,但因二者始终接触,因此两物体的速度沿垂直接触面方向的分速度大小是相等的。
用绳连接的物体的“关联”问题:
(单选)如图所示,水平面上有一汽车A,通过定滑轮用绳子拉同一水平面的物体B,当拉至图示位置时,两绳子与水平面的夹角分别为α、β,二者速度分别为vA和vB,则( )
A.vA∶vB=1∶1
B.vA∶vB=sin α∶sin β
C.vA∶vB=cos β∶cos α
D.vA∶vB=sin α∶cos β
C
用杆连接的物体的“关联”问题:
如图两根光滑的杆互相垂直地固定在一起,是国内棉分别穿有一个小球,小球a.b间用一细直棒相连。当细直棒与竖直杆夹角为? 时,求小球a.b实际速度大小之比。
【答案】Va/Vb=tanθ
相互接触的物体的“关联”问题:
如图所示,斜劈B的倾角为30°,劈尖顶着竖直墙壁静止于水平地面上,现将一半径为r的球A放在墙面与斜劈之间,并从图示位置由静止释放,不计一切摩擦,求某一时刻两物体的瞬时速度VA与VB的大小的比值?
一、关联速度问题
总结四个关键点:
①确定研究对象——绳、杆的端点或面接触点,分解的是速度方向不在绳、杆的方向上的物体(即v平行于绳,不分解;v不平行于绳,要分解);
②确定合运动(合速度)——实际的运动一定是合运动;
③确定分运动(分速度)——一般沿绳、杆的方向和垂直于绳、杆的方向;
④沿绳、杆或接触面间弹力方向的分速度相等。
一、关联速度问题
针对练习1:质量为m的物体P置于倾角为θ1的固定光滑斜面上,轻细绳跨过光滑定滑轮分别连接着P与小车,P与滑轮间的细绳平行于斜面,小车以速率v水平向右做匀速直线运动.当小车与滑轮间的细绳和水平方向成夹角θ2时(如图),下列判断正确的是( )
A.P的速率为v
B.P的速率为vcosθ2
C.绳的拉力等于mgsinθ1
D.绳的拉力小于mgsinθ1
B
针对练习2:如图所示,一条细绳跨过定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直杆上,两物体均保持静止,不计绳与滑轮、B与竖直杆间的摩擦,已知绳与竖直杆间的夹角为θ,则物体A、B的质量之比mA:mB等于( )
A.cosθ:1
B.1:cosθ
C.tanθ:1
D.1:sinθ
B
针对练习3:如图所示,在光滑的水平地面上有一个表面光滑的立方体M,一轻杆L与水平地面成α角,轻杆的下端用光滑铰链连接于O点,O点固定于地面上,轻杆的上端连接着一个小球m,小球靠在立方体左侧,立方体右侧受到水平向左推力F的作用,整个装置处于静止状态.若现在撤去水平推力F,则下列说法中正确的是( )
A.在小球和立方体分离前,若小球的速度大小为v1,
立方体的速度大小为v2,则有v1=v2sinα
B.小球在落地的瞬间和立方体分离
C.小球和立方体分离时小球只受重力
D.立方体最终将做匀速直线运动
D
针对练习4:固定在竖直平面内的半圆形刚性铁环,半径为R,铁环上穿着小球,铁环圆心O的正上方固定一个小定滑轮。用一条不可伸长的细绳,通过定滑轮以一定速度拉着小球从A点开始沿铁环运动,某时刻角度关系如图所示,若绳末端速度为v,则小球此时的速度为( )
A. B. C. D.2v
A
课后作业:
完成第五章第一节相关练习
预习第五章第二节相关知识
