5.2平抛运动(类平抛和斜抛运动)—2020-2021学年人教版高中物理必修二课件24张PPT
文档属性
| 名称 | 5.2平抛运动(类平抛和斜抛运动)—2020-2021学年人教版高中物理必修二课件24张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 1007.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-19 00:21:23 | ||
图片预览







文档简介
5.2平抛运动
(类平抛和斜抛问题)
人教版 高中物理必修二
第五章曲线运动
平抛运动的初速度水平,只受与初速度垂直的竖直向下的重力,a=g;类平抛运动的初速度不一定水平,但合外力与初速度方向垂直且为恒力,a=F合/m。
一、类平抛运动
定义
物体在某个方向做匀速直线运动,在垂直于该方向的方向做初速度为零的匀加速直线运动(受恒定的合外力)
受力特点
物体所受合外力为恒力,且与初速度方向垂直
运动特点
在初速度v0方向做匀速直线运动,在合力方向做初速度为零的匀加速直线运动,加速度为a=F合/m
处理方法
常规分解
将类平抛运动分解为沿初速度方向的匀速直线运动和垂直与初速度方向的匀加速直线运动,两个分运动彼此独立,互不影响,且与合运动具有等时性
特殊分解
对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为ax,ay,速度v分解为vx,vy,然后分别在x、y方向列方程求解
一、类平抛运动
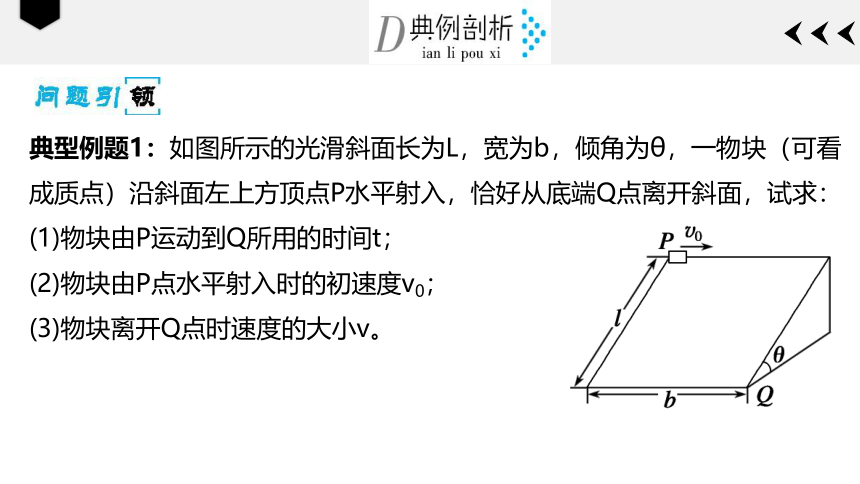
典型例题1:如图所示的光滑斜面长为L,宽为b,倾角为θ,一物块(可看成质点)沿斜面左上方顶点P水平射入,恰好从底端Q点离开斜面,试求:
(1)物块由P运动到Q所用的时间t;
(2)物块由P点水平射入时的初速度v0;
(3)物块离开Q点时速度的大小v。
一、类平抛运动
【规律总结】
①类平抛运动与平抛运动的处理方法相同,但要搞清楚其加速度的大小和方向;
②需注意的是,类平抛运动的初速度的方向不一定是水平方向,合力的方向不一定是竖直方向,一般情况下加速度a≠g。
【求解类平抛运动问题的关键】
①对研究对象受力分析,找到合外力的大小、方向,正确求出加速度。
②确定是研究速度,还是研究位移。
③把握好分解的思想方法,例题中研究位移,把运动分解成沿斜面的匀加速直线运动和水平方向的匀速直线运动,然后将两个方向的运动用时间t联系起来。
二、斜抛运动
情境导入
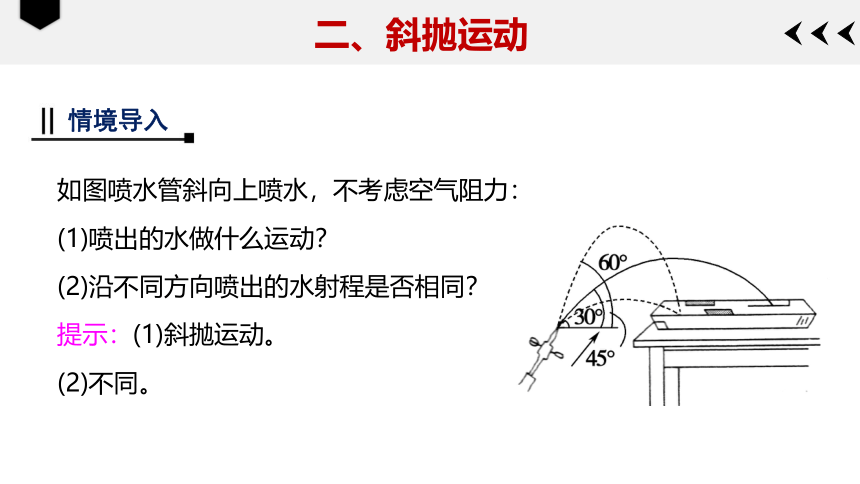
如图喷水管斜向上喷水,不考虑空气阻力:
(1)喷出的水做什么运动?
(2)沿不同方向喷出的水射程是否相同?
提示:(1)斜抛运动。
(2)不同。
二、斜抛运动
斜抛运动
1.定义:将物体以初速度v0斜向上方或斜向下方抛出,物体只在重力作用下的运动。
2.性质:斜抛运动是加速度为g的匀变速曲线运动,运动轨迹是曲线。
3.研究方法:运动的合成与分解
(1)水平方向:匀速直线运动;
(2)竖直方向:匀变速直线运动。
4.基本规律(以斜上抛运动为例,如图所示)
(1)水平方向:v0x= v0cos θ,F合x=0;
(2)竖直方向:v0y= v0sin θ,F合y=mg。
二、斜抛运动
5.常见斜抛类型:斜上抛运动和斜下抛运动
比较
斜上抛运动
斜下抛运动
运动分解
水平方向的匀速直线运动和竖直方向的竖直上抛运动的合运动
水平方向的匀速直线运动和竖直向下的匀加速直线运动的合运动
示意图像
二、斜抛运动
比较
斜上抛运动
斜下抛运动
速度公式
水平方向:vx=v0cosθ
竖直方向:vy=v0sinθ-gt
水平方向:vx=v0cos θ
竖直方向:vy=v0sin θ+gt
位移公式(位置坐标)
x=v0cosθ·t
y=v0sinθ·t-0.5gt2
x=v0cosθ·t
y=v0sinθ·t+0.5gt2
典型例题2:从某高处以6 m/s的初速度、30°抛射角斜向上方抛出一石子,落地时石子的速度方向和水平线的夹角为60°,求石子在空中运动的时间和抛出点离地面的高度(g取10 m/s2).
取向上为正方向,落地时竖直速度向下,则-vy=v0sin 30°-gt,
得t=1.2 s;由竖直方向位移公式得:
h=v0sin 30°·t-0.5gt2=3×1.2 m-5×1.22 m=-3.6 m,
负号表示落地点比抛出点低.即抛出点离地面的高度为3.6 m.
二、斜抛运动
规律总结:
解决斜抛运动问题的基本方法同平抛运动,仍是将位移或速度分解为水平方向和竖直方向,利用直线运动规律求解.本题中利用几何关系求出竖直方向上的初、末速度,利用速度公式v=v0+at可解得时间t,再利用位移公式s=v0t+0.5at2可求得抛出点离地面的高度.
典型例题3:(多选)如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,两球运动的最大高度相同。空气阻力不计,则 ( )
A.B的加速度比A的大
B.B的飞行时间比A的长
C.B在最高点的速度比A在最高点的大
D.B在落地时的速度比A在落地时的大
CD
解析:A、B两球都做斜上抛运动,只受重力作用,加速度即为重力加速度,A项错误;在竖直方向上做竖直上抛运动,由于能上升的竖直高度相同,竖直分速度相等,所以两小球在空中飞行的时间相等,B项错误;由于B球的水平射程比较大,故B球的水平速度比A球的水平速度大,而在最高点时小球的速度为小球抛出时的水平分速度,C项正确;小球B抛出时的速度大于小球A抛出时的速度,根据速度的对称性,B在落地时的速度也比A在落地时的速度大,D正确。
二、斜抛运动
斜抛运动的对称性
(1)轨迹对称:斜抛运动的轨迹为抛物线,升弧与降弧关于过最高点的竖直线对称;
(2)速度对称:关于最高点的竖直线对称的两点速度大小相等,水平分速度方向相同而竖直分速度方向相反;
(3)时间对称:运动轨迹关于过最高点的竖直线对称的物体上升与下降时间相等。
在倾角为α、斜面长为l的光滑斜面顶端,沿斜面水平方向以初速度v0抛出一小球,如图所示,小球滑到底端时在水平方向的位移s多大?
解析:小球的运动是类平抛运动,分析小球的受力情况可知,它受斜面的支持力和重力两个力的作用,合外力为重力沿斜面方向的分力F=mgsin α,其方向为沿斜面向下,产生加速度a=F/m=gsin α.在v0方向上小球不受力的作用,故小球在此方向上做匀速运动,则s=v0t……①,在与v0方向垂直沿斜面向下的方向上,小球做初速度为零的匀加速运动,
如图所示,两个足够大的倾角分别为30°、45°的光滑斜面放在同一水平面上,两斜面间距大于小球直径,斜面高度相等,有三个完全相同的小球a、b、c,开始均静止于斜面同一高度处,其中b小球在两斜面之间。若同时释放a、b、c小球到达该水平面的时间分别为t1、t2、t3。若同时沿水平方向抛出,初速度方向如图所示,到达水平面的时间分别为t1′、t2′、t3′。下列关于时间的关系不正确的是( )
A. t1>t3>t2 B. t1=t1′、t2=t2′、t3=t3′
C. t1′>t3′>t2′ D. t1D
(多选)如图所示,在水平地面同一位置的三个小球做斜上抛运动,沿三条不同的路径运动最终落在1、2、3三点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
A.落在1的小球抛出时的速率最大
B.落在3的小球在空中运动时间最短
C.三个小球运动时相同时间内速度变化相同
D.三个小球运动到最高点时速度相等
AC
(多选)如图所示,一物体以初速度v0做斜抛运动,v0与水平方向成θ角。AB连线水平,则从A到B的过程中,下列说法正确的是 ( )
A.A点与B点的速度大小相等
B.从A点到B点的时间为v0/g
C.在最高点速度为0
D.在最高点速度不为0
AD
课后作业:
完成类平抛和斜抛运动相关练习
预习《5.3实验:研究平抛运动》相关知识
(类平抛和斜抛问题)
人教版 高中物理必修二
第五章曲线运动
平抛运动的初速度水平,只受与初速度垂直的竖直向下的重力,a=g;类平抛运动的初速度不一定水平,但合外力与初速度方向垂直且为恒力,a=F合/m。
一、类平抛运动
定义
物体在某个方向做匀速直线运动,在垂直于该方向的方向做初速度为零的匀加速直线运动(受恒定的合外力)
受力特点
物体所受合外力为恒力,且与初速度方向垂直
运动特点
在初速度v0方向做匀速直线运动,在合力方向做初速度为零的匀加速直线运动,加速度为a=F合/m
处理方法
常规分解
将类平抛运动分解为沿初速度方向的匀速直线运动和垂直与初速度方向的匀加速直线运动,两个分运动彼此独立,互不影响,且与合运动具有等时性
特殊分解
对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为ax,ay,速度v分解为vx,vy,然后分别在x、y方向列方程求解
一、类平抛运动
典型例题1:如图所示的光滑斜面长为L,宽为b,倾角为θ,一物块(可看成质点)沿斜面左上方顶点P水平射入,恰好从底端Q点离开斜面,试求:
(1)物块由P运动到Q所用的时间t;
(2)物块由P点水平射入时的初速度v0;
(3)物块离开Q点时速度的大小v。
一、类平抛运动
【规律总结】
①类平抛运动与平抛运动的处理方法相同,但要搞清楚其加速度的大小和方向;
②需注意的是,类平抛运动的初速度的方向不一定是水平方向,合力的方向不一定是竖直方向,一般情况下加速度a≠g。
【求解类平抛运动问题的关键】
①对研究对象受力分析,找到合外力的大小、方向,正确求出加速度。
②确定是研究速度,还是研究位移。
③把握好分解的思想方法,例题中研究位移,把运动分解成沿斜面的匀加速直线运动和水平方向的匀速直线运动,然后将两个方向的运动用时间t联系起来。
二、斜抛运动
情境导入
如图喷水管斜向上喷水,不考虑空气阻力:
(1)喷出的水做什么运动?
(2)沿不同方向喷出的水射程是否相同?
提示:(1)斜抛运动。
(2)不同。
二、斜抛运动
斜抛运动
1.定义:将物体以初速度v0斜向上方或斜向下方抛出,物体只在重力作用下的运动。
2.性质:斜抛运动是加速度为g的匀变速曲线运动,运动轨迹是曲线。
3.研究方法:运动的合成与分解
(1)水平方向:匀速直线运动;
(2)竖直方向:匀变速直线运动。
4.基本规律(以斜上抛运动为例,如图所示)
(1)水平方向:v0x= v0cos θ,F合x=0;
(2)竖直方向:v0y= v0sin θ,F合y=mg。
二、斜抛运动
5.常见斜抛类型:斜上抛运动和斜下抛运动
比较
斜上抛运动
斜下抛运动
运动分解
水平方向的匀速直线运动和竖直方向的竖直上抛运动的合运动
水平方向的匀速直线运动和竖直向下的匀加速直线运动的合运动
示意图像
二、斜抛运动
比较
斜上抛运动
斜下抛运动
速度公式
水平方向:vx=v0cosθ
竖直方向:vy=v0sinθ-gt
水平方向:vx=v0cos θ
竖直方向:vy=v0sin θ+gt
位移公式(位置坐标)
x=v0cosθ·t
y=v0sinθ·t-0.5gt2
x=v0cosθ·t
y=v0sinθ·t+0.5gt2
典型例题2:从某高处以6 m/s的初速度、30°抛射角斜向上方抛出一石子,落地时石子的速度方向和水平线的夹角为60°,求石子在空中运动的时间和抛出点离地面的高度(g取10 m/s2).
取向上为正方向,落地时竖直速度向下,则-vy=v0sin 30°-gt,
得t=1.2 s;由竖直方向位移公式得:
h=v0sin 30°·t-0.5gt2=3×1.2 m-5×1.22 m=-3.6 m,
负号表示落地点比抛出点低.即抛出点离地面的高度为3.6 m.
二、斜抛运动
规律总结:
解决斜抛运动问题的基本方法同平抛运动,仍是将位移或速度分解为水平方向和竖直方向,利用直线运动规律求解.本题中利用几何关系求出竖直方向上的初、末速度,利用速度公式v=v0+at可解得时间t,再利用位移公式s=v0t+0.5at2可求得抛出点离地面的高度.
典型例题3:(多选)如图所示,从地面上同一位置抛出两小球A、B,分别落在地面上的M、N点,两球运动的最大高度相同。空气阻力不计,则 ( )
A.B的加速度比A的大
B.B的飞行时间比A的长
C.B在最高点的速度比A在最高点的大
D.B在落地时的速度比A在落地时的大
CD
解析:A、B两球都做斜上抛运动,只受重力作用,加速度即为重力加速度,A项错误;在竖直方向上做竖直上抛运动,由于能上升的竖直高度相同,竖直分速度相等,所以两小球在空中飞行的时间相等,B项错误;由于B球的水平射程比较大,故B球的水平速度比A球的水平速度大,而在最高点时小球的速度为小球抛出时的水平分速度,C项正确;小球B抛出时的速度大于小球A抛出时的速度,根据速度的对称性,B在落地时的速度也比A在落地时的速度大,D正确。
二、斜抛运动
斜抛运动的对称性
(1)轨迹对称:斜抛运动的轨迹为抛物线,升弧与降弧关于过最高点的竖直线对称;
(2)速度对称:关于最高点的竖直线对称的两点速度大小相等,水平分速度方向相同而竖直分速度方向相反;
(3)时间对称:运动轨迹关于过最高点的竖直线对称的物体上升与下降时间相等。
在倾角为α、斜面长为l的光滑斜面顶端,沿斜面水平方向以初速度v0抛出一小球,如图所示,小球滑到底端时在水平方向的位移s多大?
解析:小球的运动是类平抛运动,分析小球的受力情况可知,它受斜面的支持力和重力两个力的作用,合外力为重力沿斜面方向的分力F=mgsin α,其方向为沿斜面向下,产生加速度a=F/m=gsin α.在v0方向上小球不受力的作用,故小球在此方向上做匀速运动,则s=v0t……①,在与v0方向垂直沿斜面向下的方向上,小球做初速度为零的匀加速运动,
如图所示,两个足够大的倾角分别为30°、45°的光滑斜面放在同一水平面上,两斜面间距大于小球直径,斜面高度相等,有三个完全相同的小球a、b、c,开始均静止于斜面同一高度处,其中b小球在两斜面之间。若同时释放a、b、c小球到达该水平面的时间分别为t1、t2、t3。若同时沿水平方向抛出,初速度方向如图所示,到达水平面的时间分别为t1′、t2′、t3′。下列关于时间的关系不正确的是( )
A. t1>t3>t2 B. t1=t1′、t2=t2′、t3=t3′
C. t1′>t3′>t2′ D. t1
(多选)如图所示,在水平地面同一位置的三个小球做斜上抛运动,沿三条不同的路径运动最终落在1、2、3三点,三条路径的最高点是等高的,若忽略空气阻力的影响,下列说法正确的是( )
A.落在1的小球抛出时的速率最大
B.落在3的小球在空中运动时间最短
C.三个小球运动时相同时间内速度变化相同
D.三个小球运动到最高点时速度相等
AC
(多选)如图所示,一物体以初速度v0做斜抛运动,v0与水平方向成θ角。AB连线水平,则从A到B的过程中,下列说法正确的是 ( )
A.A点与B点的速度大小相等
B.从A点到B点的时间为v0/g
C.在最高点速度为0
D.在最高点速度不为0
AD
课后作业:
完成类平抛和斜抛运动相关练习
预习《5.3实验:研究平抛运动》相关知识
