2020-2021学年高二下学期物理人教版(2019)选择性必修第三册课件:2.2气体的等温变化16张PPT
文档属性
| 名称 | 2020-2021学年高二下学期物理人教版(2019)选择性必修第三册课件:2.2气体的等温变化16张PPT |  | |
| 格式 | pptx | ||
| 文件大小 | 497.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-19 00:23:28 | ||
图片预览





文档简介
2 气体的等温变化
1.学会通过实验的方法研究问题,探究物理规律,体验科学探究过程。
2.理解气体等温变化的p-V图像的物理意义。
3.理解一定质量的气体,在温度不变的情况下压强与体积的关系。
4.学会用玻意耳定律解决有关的问题。
1.气体的状态参量
研究气体的性质,用① 压强????、② 体积????、③ 温度????等物理量描述气体的
状态。这三个状态参量之间是有联系的。
2.等温变化
一定质量的气体,在④ 温度????不变的条件下,其压强与⑤ 体积????变化时的关
系。
1 | 等温变化
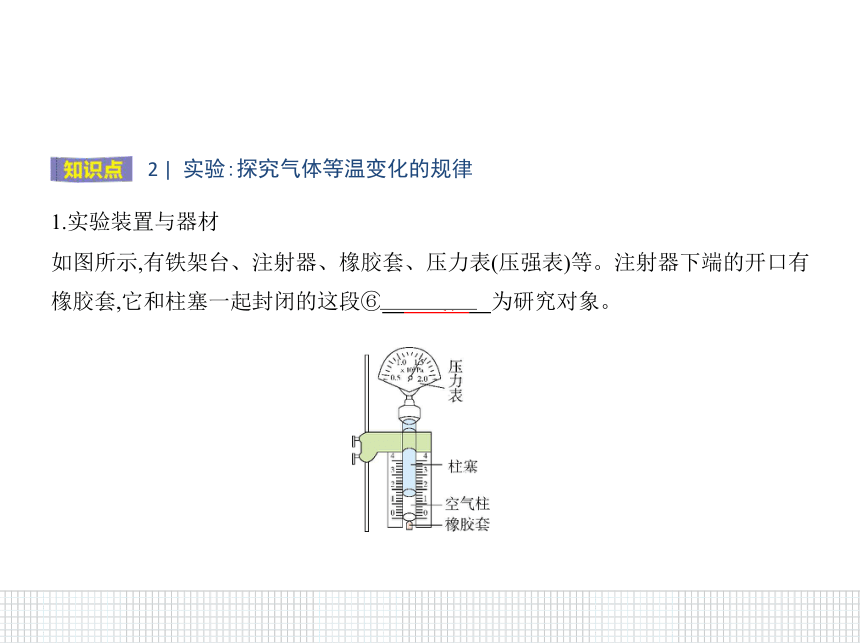
1.实验装置与器材
如图所示,有铁架台、注射器、橡胶套、压力表(压强表)等。注射器下端的开口有
橡胶套,它和柱塞一起封闭的这段⑥ 空气柱????为研究对象。
2 | 实验:探究气体等温变化的规律
2.实验思路
(1)针对气体的研究,我们可以先选定一个热力学系统,比如一定⑦ 质量????的空气,
在温度不变的情况下,测量气体在不同体积时的压强,再分析气体压强与体积的关
系。
(2)在实验过程中,一方面让空气柱内气体的质量不变;另一方面,让空气柱的体积变
化不要太快,保证⑧ 温度????不发生明显的变化。
3.物理量的测量
(1)测量空气柱的体积V:空气柱的长度l可以通过刻度尺读取,空气柱的长度l与
⑨????横截面积S????的乘积就是它的体积V。
(2)测量空气柱的压强p:空气柱的压强p可以从与注射器内空气柱相连的
⑩ 压力表????读取。
(3)把柱塞缓慢地向下压或向上拉,读取空气柱的长度与压强的几组数据。
4.数据分析与结论
(1)用p-V图像分析。用采集的各组数据在坐标纸上描点,绘制曲线,由于它描述的是
温度不变时气体压强与体积的关系,因此称它为? 等温????线。若绘制的p-V图像
类似于双曲线,那么可以猜想,空气柱的压强是否跟体积成反比。
(2)用p-?图像分析。把采集的各组数据在坐标纸上描点,p-?图像中的各点位于过
? 原点????的同一条? 直线????上,说明压强跟体积的? 倒数????成正比,即压强
与体积成? 反????比。
(1)内容:一定质量的某种气体,在温度不变的情况下,压强p与体积V成? 反????
比。
(2)公式:?????pV=C????,式中C是常量。或者?????p1V1=p2V2????,其中p1、V1和p2、V2分
别表示气体在不同状态下的压强和体积。
3 | 玻意耳定律
1.在“探究气体等温变化的规律”的实验中,应保持被封闭气体的质量和温度不发
生变化。?( √ )
2.在“探究气体等温变化的规律”的实验中,空气柱体积变化快慢对实验没有影
响。?(????? )
3.在“探究气体等温变化的规律”的实验中,被封闭气体的质量发生变化不影响实
验结果。?(????? )
4.描述气体状态的参量是密度、压强、温度。?(????? )
提示:描述气体状态的参量是压强、体积、温度。
5.在探究气体压强、体积、温度三个状态参量之间关系时采用控制变量法。(????√ )
提示:在探究气体压强、体积、温度三个状态参量之间关系时采用控制变量法。
判断正误,正确的画“ √” ,错误的画“ ?” 。
6.一定质量的气体压强跟体积成反比。?(????? )
提示:一定质量的气体在温度不变的条件下,压强跟体积成反比。
7.玻意耳定律公式pV=C中的C是与气体的种类、质量、温度无关的常量?(????? )
提示:玻意耳定律公式pV=C中的C是与气体的种类、质量、温度有关的常量。
8.若一定质量的气体的温度、压强保持不变,其体积可能发生变化。?(????? )
提示:若一定质量的气体的温度、压强保持不变,其体积也不可能发生变化。
9.一定质量的某种气体等温变化的p-V图像是通过原点的倾斜直线。?(????? )
提示:一定质量的某种气体等温变化的p-V图像是双曲线的一支。
1 | 封闭气体压强的计算
情境????如图是输液装置的一部分,药水瓶上插着两根管,一根输液管b,一根“闲
置”管a。在输液过程中,当瓶中的药水通过导管b流入人的静脉中时,外面的空气
会自动通过插在瓶塞上的另一个“闲置”管a进入瓶中。
问题
1.瓶中气室A中的压强随液面的下降将怎样变化?
提示:因a管与大气相通,则a管顶端处的液体压强等于大气压强,随着液面的下降,A
中的压强将减小。
2.若气室A、B中的压强分别为pA、pB,则它们与外界大气压强p0间存在什么样的大
小关系?
提示:因pAp0,所以pB>p0>pA。
3.人体静脉血管中的压强是保持不变的。当输液瓶悬挂高度与输液软管内径确定
的情况下,在瓶中液面下降过程中气室B中的压强是否变化?
提示:由于人体静脉血管中的压强是保持不变的,当输液瓶悬挂高度与输液软管内
径确定的情况下,瓶中液面下降过程中气室B中的压强不变。
液柱类
(1)液柱产生的附加压强:p=ρgh,其中h表示液柱或两液面之间的竖直高度,g是液柱
所在处的重力加速度。
(2)连通器原理:在连通器中,同一液体(中间液体不间断)的同一水平液面上的压强
是相等的。
如图所示,C、D液面水平且等高,液体密度为ρ,重力加速度为g,其他条件已标于图
上,则同一液面C、D两处压强相等,封闭气体A的压强pA=pC=pD=p0+ρgh。
?
活塞类
以与封闭气体接触的固体(如汽缸或活塞)为研究对象,进行受力分析,列平衡方程
求压强。
如图甲所示,汽缸置于水平地面上,汽缸横截面积为S,活塞质量为m,设大气压强为p
0,重力加速度为g。以活塞为研究对象,受力分析如图乙,由平衡条件得mg+p0S=pS,
则封闭气体的压强p=p0+?。
实验条件
(1)保证气体的质量不变:实验前将橡皮套戴牢固,在柱塞上涂好润滑油避免漏气,以
保证气体的质量不变。
(2)保证气体的温度不变:缓慢改变气体体积,并防止手接触注射器,等稳定后再读出
气体压强,以保证气体的温度不变。
实验数据的处理
(1)用p-V图像处理数据时,得到的图线是曲线;用p-?图像处理数据时,得到的图线是
过原点的直线,图线的斜率等于p与V的乘积,且保持不变。
(2)应使收集的实验数据在p-?坐标系中分布均匀。p-?图像中的某一点表示气体
所处的某一状态,图像中的某一线段表示气体的状态变化的某一过程。
2 | “探究气体等温变化的规律”的实验要点
对玻意耳定律的理解
(1)成立条件:玻意耳定律是实验定律,只有在气体质量一定、温度不变且压强不太
大、温度不太低的条件下才成立。
(2)公式:?=?,或p1V1=p2V2。
式中,p1、V1和p2、V2分别表示一定质量的气体在温度不变的情况下,处于不同的两
个状态时的压强和体积。
(3)常量的定义:p1V1=p2V2=C,该常量C与气体的种类、质量、温度有关,对一定质量
的气体,温度越高,该常量C越大。
3 | 玻意耳定律的理解与应用
应用玻意耳定律解题的基本思路
(1)明确研究对象
根据题意确定所研究的气体,要求气体质量不变,温度不变;气体的质量发生变化时,
需通过设想,把变质量转化为定质量,才能应用玻意耳定律。
(2)明确状态参量
找出气体变化前后的初、末状态,并确定初、末状态的p、V值。
(3)列方程、求解
根据玻意耳定律列方程,必要时还应用力学或几何知识列出辅助方程;求解时注意
同一物理量的单位要统一。因为是比例式,计算中只需使相应量(p1、p2及V1、V2)
的单位统一,不一定用国际单位制的单位。
(4)检验结果
在等温变化中,有时列方程求解会得到两个结果,应通过合理性的检验决定取舍。
两种等温变化的图像
1.学会通过实验的方法研究问题,探究物理规律,体验科学探究过程。
2.理解气体等温变化的p-V图像的物理意义。
3.理解一定质量的气体,在温度不变的情况下压强与体积的关系。
4.学会用玻意耳定律解决有关的问题。
1.气体的状态参量
研究气体的性质,用① 压强????、② 体积????、③ 温度????等物理量描述气体的
状态。这三个状态参量之间是有联系的。
2.等温变化
一定质量的气体,在④ 温度????不变的条件下,其压强与⑤ 体积????变化时的关
系。
1 | 等温变化
1.实验装置与器材
如图所示,有铁架台、注射器、橡胶套、压力表(压强表)等。注射器下端的开口有
橡胶套,它和柱塞一起封闭的这段⑥ 空气柱????为研究对象。
2 | 实验:探究气体等温变化的规律
2.实验思路
(1)针对气体的研究,我们可以先选定一个热力学系统,比如一定⑦ 质量????的空气,
在温度不变的情况下,测量气体在不同体积时的压强,再分析气体压强与体积的关
系。
(2)在实验过程中,一方面让空气柱内气体的质量不变;另一方面,让空气柱的体积变
化不要太快,保证⑧ 温度????不发生明显的变化。
3.物理量的测量
(1)测量空气柱的体积V:空气柱的长度l可以通过刻度尺读取,空气柱的长度l与
⑨????横截面积S????的乘积就是它的体积V。
(2)测量空气柱的压强p:空气柱的压强p可以从与注射器内空气柱相连的
⑩ 压力表????读取。
(3)把柱塞缓慢地向下压或向上拉,读取空气柱的长度与压强的几组数据。
4.数据分析与结论
(1)用p-V图像分析。用采集的各组数据在坐标纸上描点,绘制曲线,由于它描述的是
温度不变时气体压强与体积的关系,因此称它为? 等温????线。若绘制的p-V图像
类似于双曲线,那么可以猜想,空气柱的压强是否跟体积成反比。
(2)用p-?图像分析。把采集的各组数据在坐标纸上描点,p-?图像中的各点位于过
? 原点????的同一条? 直线????上,说明压强跟体积的? 倒数????成正比,即压强
与体积成? 反????比。
(1)内容:一定质量的某种气体,在温度不变的情况下,压强p与体积V成? 反????
比。
(2)公式:?????pV=C????,式中C是常量。或者?????p1V1=p2V2????,其中p1、V1和p2、V2分
别表示气体在不同状态下的压强和体积。
3 | 玻意耳定律
1.在“探究气体等温变化的规律”的实验中,应保持被封闭气体的质量和温度不发
生变化。?( √ )
2.在“探究气体等温变化的规律”的实验中,空气柱体积变化快慢对实验没有影
响。?(????? )
3.在“探究气体等温变化的规律”的实验中,被封闭气体的质量发生变化不影响实
验结果。?(????? )
4.描述气体状态的参量是密度、压强、温度。?(????? )
提示:描述气体状态的参量是压强、体积、温度。
5.在探究气体压强、体积、温度三个状态参量之间关系时采用控制变量法。(????√ )
提示:在探究气体压强、体积、温度三个状态参量之间关系时采用控制变量法。
判断正误,正确的画“ √” ,错误的画“ ?” 。
6.一定质量的气体压强跟体积成反比。?(????? )
提示:一定质量的气体在温度不变的条件下,压强跟体积成反比。
7.玻意耳定律公式pV=C中的C是与气体的种类、质量、温度无关的常量?(????? )
提示:玻意耳定律公式pV=C中的C是与气体的种类、质量、温度有关的常量。
8.若一定质量的气体的温度、压强保持不变,其体积可能发生变化。?(????? )
提示:若一定质量的气体的温度、压强保持不变,其体积也不可能发生变化。
9.一定质量的某种气体等温变化的p-V图像是通过原点的倾斜直线。?(????? )
提示:一定质量的某种气体等温变化的p-V图像是双曲线的一支。
1 | 封闭气体压强的计算
情境????如图是输液装置的一部分,药水瓶上插着两根管,一根输液管b,一根“闲
置”管a。在输液过程中,当瓶中的药水通过导管b流入人的静脉中时,外面的空气
会自动通过插在瓶塞上的另一个“闲置”管a进入瓶中。
问题
1.瓶中气室A中的压强随液面的下降将怎样变化?
提示:因a管与大气相通,则a管顶端处的液体压强等于大气压强,随着液面的下降,A
中的压强将减小。
2.若气室A、B中的压强分别为pA、pB,则它们与外界大气压强p0间存在什么样的大
小关系?
提示:因pA
3.人体静脉血管中的压强是保持不变的。当输液瓶悬挂高度与输液软管内径确定
的情况下,在瓶中液面下降过程中气室B中的压强是否变化?
提示:由于人体静脉血管中的压强是保持不变的,当输液瓶悬挂高度与输液软管内
径确定的情况下,瓶中液面下降过程中气室B中的压强不变。
液柱类
(1)液柱产生的附加压强:p=ρgh,其中h表示液柱或两液面之间的竖直高度,g是液柱
所在处的重力加速度。
(2)连通器原理:在连通器中,同一液体(中间液体不间断)的同一水平液面上的压强
是相等的。
如图所示,C、D液面水平且等高,液体密度为ρ,重力加速度为g,其他条件已标于图
上,则同一液面C、D两处压强相等,封闭气体A的压强pA=pC=pD=p0+ρgh。
?
活塞类
以与封闭气体接触的固体(如汽缸或活塞)为研究对象,进行受力分析,列平衡方程
求压强。
如图甲所示,汽缸置于水平地面上,汽缸横截面积为S,活塞质量为m,设大气压强为p
0,重力加速度为g。以活塞为研究对象,受力分析如图乙,由平衡条件得mg+p0S=pS,
则封闭气体的压强p=p0+?。
实验条件
(1)保证气体的质量不变:实验前将橡皮套戴牢固,在柱塞上涂好润滑油避免漏气,以
保证气体的质量不变。
(2)保证气体的温度不变:缓慢改变气体体积,并防止手接触注射器,等稳定后再读出
气体压强,以保证气体的温度不变。
实验数据的处理
(1)用p-V图像处理数据时,得到的图线是曲线;用p-?图像处理数据时,得到的图线是
过原点的直线,图线的斜率等于p与V的乘积,且保持不变。
(2)应使收集的实验数据在p-?坐标系中分布均匀。p-?图像中的某一点表示气体
所处的某一状态,图像中的某一线段表示气体的状态变化的某一过程。
2 | “探究气体等温变化的规律”的实验要点
对玻意耳定律的理解
(1)成立条件:玻意耳定律是实验定律,只有在气体质量一定、温度不变且压强不太
大、温度不太低的条件下才成立。
(2)公式:?=?,或p1V1=p2V2。
式中,p1、V1和p2、V2分别表示一定质量的气体在温度不变的情况下,处于不同的两
个状态时的压强和体积。
(3)常量的定义:p1V1=p2V2=C,该常量C与气体的种类、质量、温度有关,对一定质量
的气体,温度越高,该常量C越大。
3 | 玻意耳定律的理解与应用
应用玻意耳定律解题的基本思路
(1)明确研究对象
根据题意确定所研究的气体,要求气体质量不变,温度不变;气体的质量发生变化时,
需通过设想,把变质量转化为定质量,才能应用玻意耳定律。
(2)明确状态参量
找出气体变化前后的初、末状态,并确定初、末状态的p、V值。
(3)列方程、求解
根据玻意耳定律列方程,必要时还应用力学或几何知识列出辅助方程;求解时注意
同一物理量的单位要统一。因为是比例式,计算中只需使相应量(p1、p2及V1、V2)
的单位统一,不一定用国际单位制的单位。
(4)检验结果
在等温变化中,有时列方程求解会得到两个结果,应通过合理性的检验决定取舍。
两种等温变化的图像
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
