2020-2021学年高一下学期物理人教版(2019)必修第二册课件:8.4机械能守恒定律72张PPT
文档属性
| 名称 | 2020-2021学年高一下学期物理人教版(2019)必修第二册课件:8.4机械能守恒定律72张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览










文档简介
第八章 机械能守恒定律
4 机械能守恒定律
1.了解人们追寻守恒量和建立“能量”概念的漫长过程.
2.知道什么是机械能,知道物体的动能和势能可以相互转化.
3.能够推导出机械能守恒定律.
4.会判断一个过程机械能是否守恒,能运用机械能守恒定律解决
有关问题.
学习目标
知识梳理
重点探究
随堂演练
课时对点练
内容索引
NEIRONGSUOYIN
一、追寻守恒量
伽利略曾研究过小球在斜面上的运动,如图1所示.
将小球由斜面A上某位置由静止释放,如果空气阻力和摩擦力小到可以忽略,小球在斜面B上速度变为0(即到达最高点)时的高度与它出发时的高度 ,不会更高一点,也不会更低一点.这说明某种“东西”在小球运动的过程中是 的.
知识梳理
图1
相同
不变
二、动能与势能的相互转化
1.重力势能与动能的转化
只有重力做功时,若重力对物体做正功,则物体的重力势能 ,动能 ,物体的 转化为 ;若重力对物体做负功,则物体的重力势能 ,动能 ,物体的 转化为 .
2.弹性势能与动能的转化
只有弹簧弹力做功时,若弹力对物体做正功,则弹簧的弹性势能 ,物体的动能 ,弹簧的 转化为物体的 ;若弹力对物体做负功,则弹簧的弹性势能 ,物体的动能 ,物体的 转化为弹簧的 .
3.机械能: 、 与 统称为机械能.
减少
增加
重力势能
动能
增加
减少
动能
重力势能
减少
增加
弹性势能
动能
增加
减少
动能
弹性势能
重力势能
弹性势能
动能
三、机械能守恒定律
1.内容:在只有 或 做功的物体系统内, 与 可以互相转化,而 保持不变.
2.表达式: mv22+mgh2= 或Ek2+Ep2= .
3.应用机械能守恒定律解决问题只需考虑运动的_______和 ,不必考虑两个状态间 ,即可以简化计算.
重力
弹力
动能
势能
总的机械能
Ek1+Ep1
末状态
过程的细节
初状态
1.判断下列说法的正误.
(1)通过重力做功,动能和重力势能可以相互转化.( )
(2)机械能守恒时,物体一定只受重力和弹力作用.( )
(3)合力做功为零,物体的机械能一定保持不变.( )
(4)只有重力做功时,物体的机械能一定守恒.( )
即学即用
√
√
×
×
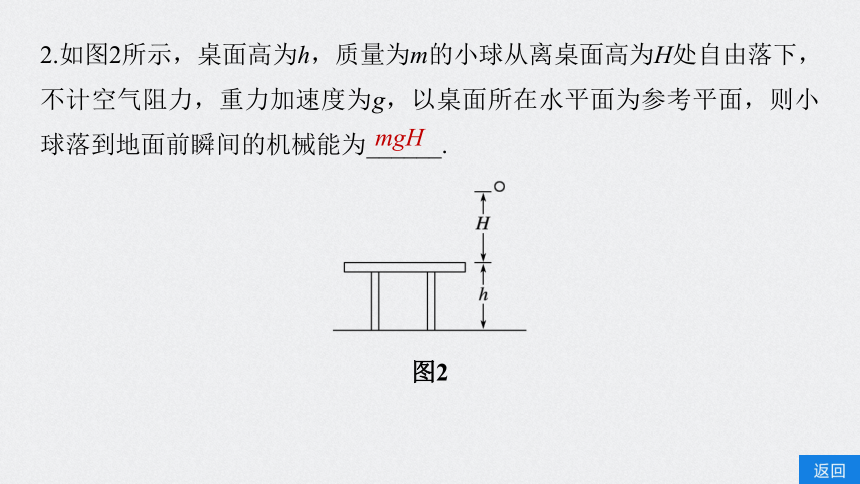
2.如图2所示,桌面高为h,质量为m的小球从离桌面高为H处自由落下,不计空气阻力,重力加速度为g,以桌面所在水平面为参考平面,则小球落到地面前瞬间的机械能为______.
图2
mgH
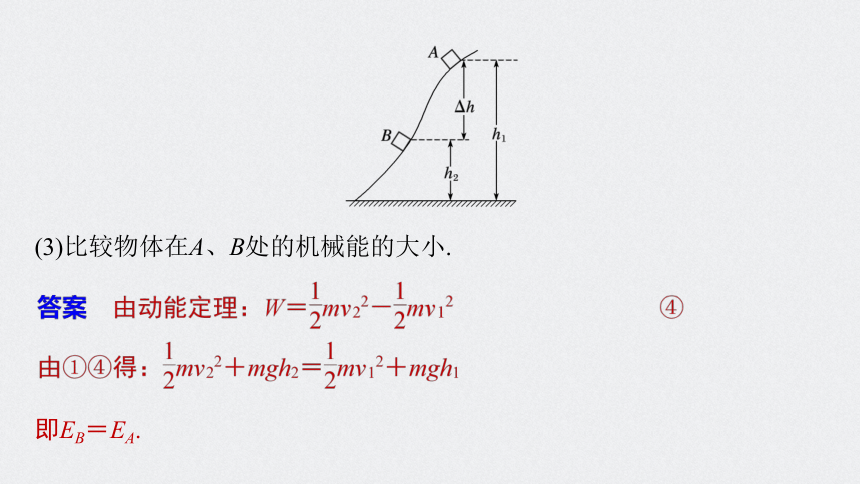
导学探究 如图3所示,质量为m的物体沿光滑曲面滑下的过程中,下落到高度为h1的A处时速度为v1,下落到高度为h2的B处时速度为v2,重力加速度为g,不计空气阻力,选择地面为参考平面.
(1)求从A至B的过程中重力做的功;
重点探究
图3
一、对机械能守恒定律的理解
答案 W=mgΔh=mg(h1-h2)=mgh1-mgh2 ①
(2)求物体在A、B处的机械能EA、EB;
(3)比较物体在A、B处的机械能的大小.
即EB=EA.
1.对机械能守恒条件的理解
(1)只有重力做功,只发生动能和重力势能的相互转化.
(2)只有弹力做功,只发生动能和弹性势能的相互转化.
(3)只有重力和弹力做功,发生动能、弹性势能、重力势能的相互转化.
(4)除受重力或弹力外,其他力也做功,但其他力做功的代数和始终为零.
知识深化
2.判断机械能是否守恒的方法
(1)做功条件分析:只有重力和系统内弹力做功,其他力不做功或做功的代数和始终为零.
(2)能量转化分析:系统内只有动能、重力势能及弹性势能的相互转化,即系统内只有物体间的机械能相互转移,则机械能守恒.
(3)定义判断法:如物体沿竖直方向或沿斜面匀速运动时,动能不变,势能变化,机械能不守恒.
例1 如图4所示,下列关于机械能是否守恒的判断正确的是
A.甲图中,物体A将弹簧压缩的过程中,
A机械能守恒
B.乙图中,A置于光滑水平面,物体B沿
光滑斜面下滑,物体B机械能守恒
C.丙图中,不计任何阻力时A加速下落、
B加速上升过程中,A、B系统机械能守恒
D.丁图中,系在橡皮条一端的小球向下摆动时,小球的机械能守恒
图4
√
解析 若不计空气阻力,题图甲中重力和弹力做功,物体A和弹簧组成的系统机械能守恒,但物体A机械能不守恒,选项A错误;
题图乙中物体B除受重力外,还受弹力,弹力对B做负功,机械能不守恒,但A、B组成的系统机械能守恒,选项B错误;
题图丙中绳子张力对A做负功,对B做正功,代数和为零,A、B系统机械能守恒,选项C正确;
题图丁中小球的重力势能转化为小球的动能和橡皮条的弹性势能,小球的机械能不守恒,选项D错误.
针对训练1 (2019·福建宁德六市高一期中联考)在下列情况中,机械能守恒的是
A.飘落的树叶
B.沿着斜面匀速下滑的物体
C.被起重机匀加速吊起的物体
D.不计空气阻力,推出的铅球在空中运动的过程
√
解析 树叶在飘落过程中,空气阻力做负功,机械能减少,故A错误;
沿着斜面匀速下滑的物体,摩擦力做功,故机械能不守恒,故B错误;
物体被起重机匀加速吊起时拉力对物体做功,故物体的机械能不守恒,故C错误;
推出的铅球在空中运动且不计空气阻力,只有重力做功,机械能守恒,故D正确.
例2 (多选)如图5,一根轻弹簧下端固定,竖立在水平面上.其上方A位置有一小球,小球从静止开始下落到B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.不计空气阻力,则小球
A.下落至C处速度最大
B.由A至D的过程中机械能守恒
C.由B至D的过程中,动能先增大后减小
D.由A运动到D时,重力势能的减少量等于弹簧弹性势能的
增加量
√
图5
√
√
解析 小球从B至C过程,重力大于弹力,合力向下,小球做加速运动,小球从C至D过程,重力小于弹力,合力向上,小球做减速运动,所以动能先增大后减小,在C点动能最大,速度最大,故A、C正确;
由A至B下落过程中小球只受重力,其机械能守恒,从B→D过程,小球和弹簧组成的系统机械能守恒,但小球的机械能不守恒,故B错误;
在D位置小球速度减小到零,小球的动能为零,则从A运动到D时,小球重力势能的减少量等于弹簧弹性势能的增加量,故D正确.
二、机械能守恒定律的应用
1.机械能守恒定律常用的三种表达式
(1)从不同状态看:Ek1+Ep1=Ek2+Ep2(或E1=E2)
此式表示系统两个状态的机械能总量相等.
(2)从能的转化角度看:ΔEk=-ΔEp
此式表示系统动能的增加(减少)量等于势能的减少(增加)量.
(3)从能的转移角度看:ΔEA增=ΔEB减
此式表示系统A部分机械能的增加量等于系统剩余部分,即B部分机械能的减少量.
2.应用机械能守恒定律解题的一般步骤
(1)根据题意选取研究对象;
(2)明确研究对象的运动过程,分析研究对象在此过程中的受力情况,弄清各力做功的情况,判断机械能是否守恒.
(3)恰当地选取参考平面,确定研究对象在此过程中的初态和末态的机械能.
(4)根据机械能守恒定律的不同表达式列方程并求解.
例3 (2019·大庆中学高一期末)一条长为0.80 m的轻绳一端固定在O点,另一端连接一质量m=0.10 kg的小球,悬点O距离水平地面的高度H=1.00 m,开始时小球处于A点,此时轻绳拉直处于水平方向上,如图6所示,让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的光滑小钉子P时立刻断裂,不计轻绳断裂的能量损失,取重力加速度g=10 m/s2,不计空气阻力,求:
(1)当小球运动到B点时的速度大小;
图6
答案 4.0 m/s
解析 设小球运动到B点时的速度大小为vB,
(2)绳断裂后球从B点抛出并落在水平地面的C点,求小球落到C点时的瞬时速度的大小.
解析 小球从B点做平抛运动,小球只受重力,全过程机械能守恒,
针对训练2 如图7所示,质量m=50 kg的跳水运动员从距水面高h=10 m的跳台上以v0=5 m/s的速度斜向上起跳,最终落入水中,若忽略运动员的身高,取g=10 m/s2,不计空气阻力.求:
(1)运动员在跳台上时具有的重力势能(以水面为参考平面);
图7
答案 5 000 J
解析 以水面为参考平面,则运动员在跳台上时具有的重力势能为
Ep=mgh=5 000 J.
(2)运动员起跳时的动能;
答案 625 J
解析 运动员起跳时的速度为v0=5 m/s,
则运动员起跳时的动能为
(3)运动员入水时的速度大小;入水时的速度大小与起跳时的方向有关吗?
答案 15 m/s 无关
解析 运动员从起跳到入水过程中,只有重力做功,运动员的机械能守恒,
此速度大小与起跳时的方向无关.
1.(机械能守恒的判断)(2019·泉州市高一下月考)下列说法中正确的是
A.图8甲中“蛟龙号”被吊车匀速吊
下水的过程中它的机械能守恒
B.图乙中物块在恒力F作用下沿固定
光滑斜面匀速上滑过程中,物块的
机械能守恒
C.图丙中物块沿固定斜面匀速下滑过程中,物块的机械能不守恒
D.图丁中撑竿跳高运动员在上升过程中机械能守恒
1
2
3
4
随堂演练
√
图8
解析 题图甲中“蛟龙号”被吊车匀速吊下水的过程中,动能不变,重力势能变小,所以机械能不守恒,故A错误;
题图乙中物块在恒力F作用下沿固定光滑斜面匀速上滑过程中,恒力F做正功,物块的机械能增加,故B错误;
题图丙中物块沿固定斜面匀速下滑过程中,物块在斜面上受力平衡,重力沿斜面向下的分力与摩擦力平衡,摩擦力做负功,物块的机械能减小,故C正确;
题图丁中撑竿跳高运动员在上升过程中,撑竿的弹性势能转化为运动员的机械能,所以运动员的机械能不守恒,故D错误.
1
2
3
4
2.(机械能守恒定律的应用)以相同大小的初速度v0将物体从同一水平面分别竖直上抛、斜上抛、沿光滑斜面(足够长)上滑,如图9所示,三种情况达到的最大高度分别为h1、h2和h3,不计空气阻力,则
A.h1=h2>h3
B.h1=h2<h3
C.h1=h3<h2
D.h1=h3>h2
1
2
3
4
√
图9
解析 竖直上抛的物体和沿光滑斜面运动的物体,上升到最高点时,速度均为0,
斜上抛的物体在最高点速度不为零,设为v1,
1
2
3
4
3.(机械能守恒定律的应用)如图10所示,由距离地面h2=1 m的高度处以v0=4 m/s的速度斜向上抛出质量为m=1 kg的物体,当其上升的高度为h1=0.4 m时到达最高点,最终落在水平地面上,现以过抛出点的水平面为参考平面,取重力加速度g=10 m/s2,不计空气阻力,则
A.物体在最大高度处的重力势能为14 J
B.物体在最大高度处的机械能为16 J
C.物体落地前瞬间的机械能为8 J
D.物体落地前瞬间的动能为8 J
1
2
3
4
√
图10
解析 物体在最高点时具有的重力势能Ep1=mgh1=1×10×0.4 J=4 J,A错误;
物体在最高点时具有的机械能等于刚抛出时的动能,即8 J,B错误;
物体在下落过程中机械能守恒,落地前在任意位置的机械能都等于8 J,C正确;
物体落地前瞬间的动能Ek=E-Ep2=E-mgh2=8 J-1×10×(-1) J=18 J,D错误.
1
2
3
4
(1)求小球在B、A两点的动能之比;
1
2
3
4
图11
答案 5∶1
解析 设小球的质量为m,小球在A点的动能为EkA,
1
2
3
4
由①②式得EkB∶EkA=5∶1 ③
(2)通过计算判断小球能否沿轨道运动到C点.
1
2
3
4
答案 见解析
解析 若小球能沿轨道运动到C点,
则小球在C点所受轨道的正压力FN应满足FN≥0 ④
设小球在C点的速度大小为vC,由牛顿第二定律有
1
2
3
4
1
2
3
4
故小球恰好可以沿轨道运动到C点.
考点一 机械能守恒的判断
1.(2019·重庆市江津中学、合川中学等七校高一下学期期末)下列描述中,机械能守恒的是
A.沿斜面匀速向上行驶的汽车
B.被匀速向上吊起的集装箱
C.在真空中水平抛出的石块
D.物体以 g的加速度竖直向上做匀减速运动
基础对点练
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
2.(2019·上饶市玉山一中高一下期中)关于机械能守恒的叙述,下列说法正确的是
A.做匀速圆周运动的物体,机械能一定守恒
B.物体所受的合力不等于零,机械能可能守恒
C.物体做匀速直线运动,机械能一定守恒
D.物体所受合力做功为零,机械能一定守恒
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
解析 若物体在竖直平面内做匀速圆周运动,动能不变,重力势能变化,机械能不守恒,故A错误;
物体所受的合力不等于零,它的机械能可能守恒,例如物体做自由落体运动,故B正确;
物体在竖直方向做匀速直线运动时,动能不变,重力势能变化,机械能不守恒,故C错误;
物体所受合力做功为零,它的动能不变,重力势能可能变化,机械能不一定守恒,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3.(多选)如图1所示,细绳的一端固定于O点,另一端系一小球,在O点的正下方钉一个钉子C.小球从一定高度处释放,不计一切阻力,细绳摆到竖直位置时,被钉子挡住,比较细绳被钉子挡住前、后瞬间
A.小球的动能变小
B.小球的动能不变
C.小球的重力势能变小
D.小球的机械能不变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
√
图1
解析 小球到达最低点时,速度方向沿水平方向,在钉子挡住细绳瞬间,合外力对小球做功为零,则小球的动能不变,故A错误,B正确;
在钉子挡住细绳瞬间,小球的质量和高度不变,则小球的重力势能不变,故C错误;
在钉子挡住细绳瞬间,小球的动能与重力势能都不变,则小球的机械能不变,故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4.(多选)(2019·三明市高一下学期期末)如图2所示,一轻弹簧一端固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在重物由A点摆到最低点的过程中
A.重物的机械能减少
B.重物与弹簧组成的系统的机械能不变
C.重物与弹簧组成的系统的机械能增加
D.重物与弹簧组成的系统的机械能减少
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
图2
√
解析 重物自由摆下的过程中,弹簧拉力对重物做负功,重物的机械能减少,选项A正确;
对重物与弹簧组成的系统而言,除重力、弹力外,无其他外力做功,故系统的机械能守恒,选项B正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
考点二 机械能守恒定律的应用
5.(2019·天津市第一中学高一下期中)如图3,在地面上以初速度v0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,重力加速度为g,若以地面为参考平面,且不计空气阻力,则
A.物体在海平面上的重力势能为mgh
B.重力对物体做的功为-mgh
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
图3
解析 以地面为参考平面,海平面低于地面的高度为h,所以物体在海平面上时的重力势能为-mgh,故A错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
重力做功与路径无关,与初、末位置的高度差有关,抛出点与海平面的高度差为h,并且重力做正功,所以整个过程重力对物体做功为mgh,故B错误;
6.(多选)(2019·江西萍乡高一下期中)如图所示,A、B、C、D四个图中的小球完全相同.现从同一高度h处由静止释放小球,小球下落同样的高度,然后进入不同的轨道.A图中的轨道是一个内径略大于小球直径的管,其上部为直管,下部为圆弧形,底端与斜面平滑衔接,管的高度高于h;B图中的轨道是半圆轨道,其直径等于h;C图中的轨道高度低于h;D图中的轨道是一段斜面,且高于h.如果不计任何阻力和拐弯处的能量损失,小球进入轨道后不能运动到h高度的图是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
√
解析 A中小球离开轨道后做竖直上抛运动,运动到最高点时的速度为零,根据机械能守恒定律得mgh+0=mgh′+0,则h=h′,故能运动到h高度;
B中小球在内轨道运动,假设小球能通过圆轨道最高点,则小球通过最高点的最小速度为v= ,故小球在最高点的速度不为零,根据机械能守恒定律可知假设不成立,故小球不能运动到h高度;
C中小球离开轨道后做斜抛运动,水平方向做匀速直线运动,运动到最高点时在水平方向上有速度,即在最高点的速度不为零,根据机械能守恒定律可知,小球不能运动到h高度;
D中小球到达右侧斜面上最高点时的速度为零,根据机械能守恒定律得mgh+0=mgh′+0,则h=h′,故能运动到h高度.故选B、C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7.(2019·北京市十一学校高一下期末)如图4所示,轻弹簧置于光滑水平面上,一端固定在竖直墙壁,另一端自由伸长.现分别用质量不相等的两物块将弹簧压缩相同长度后由静止释放,物块离开弹簧的瞬间
A.质量小的速度大
B.质量小的动能大
C.质量大的速度大
D.质量大的动能大
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
图4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8.(多选)质量相同的小球A和B分别悬挂在长为L和2L的不同长绳上,先将小球A、B拉至同一水平高度(如图5所示)从静止释放,当两绳竖直时,不计空气阻力,则
A.两球的速率一样大
B.两球的动能一样大
C.两球的机械能一样大
D.两球所受的拉力一样大
√
图5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
解析 两球在下落过程中机械能守恒,开始下落时,重力势能相等,动能都为零,所以机械能相等,下落到最低点时的机械能也一样大,选项C正确;
以小球A为研究对象,设小球到达最低点时的速度大小为vA,动能为EkA,小球所受的拉力大小为FA,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9.(多选)(2019·平顶山市高一下学期期末)蹦极是一项有趣的极限运动,轻质弹性绳的一端固定,另一端和运动员相连,运动员经一段自由下落后绳被拉直,绳的形变是弹性形变,绳处于原长时的弹性势能为零.则在运动员从静止开始自由下落,直至最低点的过程中,下列表述正确的是(整个过程中空气阻力不计)
A.运动员的机械能守恒
B.弹性绳的弹性势能先增大后减小
C.运动员与弹性绳的总机械能守恒
D.运动员动能最大时弹性绳的弹性势能不为零
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
解析 运动员开始自由下落,从弹性绳开始伸直到最低点的过程中,先是拉力增加但仍小于重力,合外力向下,运动员向下做加速度减小的加速运动,当加速度为零时,速度最大,动能最大,此后拉力大于重力且拉力继续增加,合外力向上,运动员开始做加速度增大的减速运动,速度减小,动能减小,所以运动员的机械能不守恒,但运动员与弹性绳的总机械能守恒,故A错误,C正确;
运动员开始自由下落,弹性绳的弹性势能不变,从弹性绳开始伸直到最低点的过程中,弹性绳的弹性势能增大,故B错误;
当加速度为零时,速度最大,动能最大,弹性绳的弹力等于运动员的重力,弹性绳的弹性势能不为零,故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10.(2019·大庆中学高一期末)一个小石子从高为10 m处自由下落,不计空气阻力,经一段时间后小石子的动能恰等于它的重力势能(以地面为参考平面),g=10 m/s2,则该时刻小石子的速度大小为
A.5 m/s B.10 m/s C.15 m/s D.20 m/s
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
能力综合练
解析 运动的过程中小石子的机械能守恒,
设小石子在离地高度为h′时动能等于重力势能,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
11.(多选)(2019·西安高级中学期末)一个物体以一定的初速度竖直上抛,不计空气阻力,如图所示为表示物体的动能Ek随高度h变化的图像A、物体的重力势能Ep随速度v变化的图像B(图线形状为四分之一圆弧)、物体的机械能E随高度h变化的图像C、物体的动能Ek随速度v变化的图像D(图线为开口向上的抛物线的一部分),其中可能正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
√
√
解析 设物体的初速度为v0,物体的质量为m,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
则Ep-v图像为开口向下的抛物线(第一象限中的部分),图像B错误;
由于竖直上抛运动过程中机械能守恒,所以E-h图像为一平行于h轴的直线,图像C可能正确;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12.如图6所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态,现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),重力加速度为g,则在圆环下滑到最大距离的过程中
A.圆环的机械能守恒
B.弹簧弹性势能增加了 mgL
C.圆环下滑到最大距离时,所受合力为零
D.圆环重力势能与弹簧弹性势能之和始终保持不变
√
图6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解析 圆环在下落过程中机械能减少,弹簧弹性势能增加,圆环与弹簧组成的系统机械能守恒,圆环下落到最低点时速度为零,但是加速度不为零,即合力不为零;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
圆环下落过程中重力势能、动能及弹簧弹性势能之和保持不变,故选B.
13.(多选)(2019·西安二十六中期末)如图7所示,细轻杆的一端与质量为m的小球相连,可绕O点的水平轴自由转动.现给小球一初速度,使它在竖直平面内做圆周运动,a、b分别表示轨道的最低点和最高点,重力加速度为g,则小球在这两点对杆的作用力大小之差可能为
A.3mg
B.4mg
C.5mg
D.6mg
1
2
3
4
5
6
7
8
9
10
11
12
13
14
图7
√
15
√
√
解析 小球运动到b点时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
对杆和球组成的系统,由b→a机械能守恒,
vb=0时,ΔF=4mg,若vb增大,则ΔF增大;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
此时ΔF=6mg
则ΔF=6mg
综上,A错误,B、C、D正确.
14.图8是某轻轨车站的设计方案,与站台连接的轨道有一个小坡度,电车进站要上坡,出站要下坡.已知坡高为2 m,电车到a点时的速度为25.2 km/h,此后便切断电车的电源,如果不考虑电车所受的摩擦力,电车能否冲上站台?如果电车不能冲上站台,请说明理由;如果电车能冲上站台,求它到达b点时的速度大小.(g取10 m/s2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
图8
15
答案 能 3 m/s
解析 电车电源被切断后,只有重力做功,故机械能守恒.
其中v1=25.2 km/h=7 m/s
若这些动能全部转化为重力势能,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
设电车到达b点时的速度为v2,由机械能守恒定律得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15.(2019·山师大附中高一下学期期末)如图9是一个设计“过山车”的试验装置的原理示意图,斜面AB与竖直面内的圆形轨道在B点平滑连接,斜面AB和圆形轨道都是光滑的,圆形轨道半径为R,一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,小车恰能通过圆形轨道的最高点C.已知重力加速度为g.求:
(1)A点距水平面的高度h;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案 2.5R
图9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
由A运动到C,根据机械能守恒定律得:
解得:h=2.5R
(2)运动到B点时小车对圆形轨道压力的大小.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案 6mg
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解得:FN=6mg
由牛顿第三定律可知,运动到B点时小车对圆形轨道的压力大小为6mg.
4 机械能守恒定律
1.了解人们追寻守恒量和建立“能量”概念的漫长过程.
2.知道什么是机械能,知道物体的动能和势能可以相互转化.
3.能够推导出机械能守恒定律.
4.会判断一个过程机械能是否守恒,能运用机械能守恒定律解决
有关问题.
学习目标
知识梳理
重点探究
随堂演练
课时对点练
内容索引
NEIRONGSUOYIN
一、追寻守恒量
伽利略曾研究过小球在斜面上的运动,如图1所示.
将小球由斜面A上某位置由静止释放,如果空气阻力和摩擦力小到可以忽略,小球在斜面B上速度变为0(即到达最高点)时的高度与它出发时的高度 ,不会更高一点,也不会更低一点.这说明某种“东西”在小球运动的过程中是 的.
知识梳理
图1
相同
不变
二、动能与势能的相互转化
1.重力势能与动能的转化
只有重力做功时,若重力对物体做正功,则物体的重力势能 ,动能 ,物体的 转化为 ;若重力对物体做负功,则物体的重力势能 ,动能 ,物体的 转化为 .
2.弹性势能与动能的转化
只有弹簧弹力做功时,若弹力对物体做正功,则弹簧的弹性势能 ,物体的动能 ,弹簧的 转化为物体的 ;若弹力对物体做负功,则弹簧的弹性势能 ,物体的动能 ,物体的 转化为弹簧的 .
3.机械能: 、 与 统称为机械能.
减少
增加
重力势能
动能
增加
减少
动能
重力势能
减少
增加
弹性势能
动能
增加
减少
动能
弹性势能
重力势能
弹性势能
动能
三、机械能守恒定律
1.内容:在只有 或 做功的物体系统内, 与 可以互相转化,而 保持不变.
2.表达式: mv22+mgh2= 或Ek2+Ep2= .
3.应用机械能守恒定律解决问题只需考虑运动的_______和 ,不必考虑两个状态间 ,即可以简化计算.
重力
弹力
动能
势能
总的机械能
Ek1+Ep1
末状态
过程的细节
初状态
1.判断下列说法的正误.
(1)通过重力做功,动能和重力势能可以相互转化.( )
(2)机械能守恒时,物体一定只受重力和弹力作用.( )
(3)合力做功为零,物体的机械能一定保持不变.( )
(4)只有重力做功时,物体的机械能一定守恒.( )
即学即用
√
√
×
×
2.如图2所示,桌面高为h,质量为m的小球从离桌面高为H处自由落下,不计空气阻力,重力加速度为g,以桌面所在水平面为参考平面,则小球落到地面前瞬间的机械能为______.
图2
mgH
导学探究 如图3所示,质量为m的物体沿光滑曲面滑下的过程中,下落到高度为h1的A处时速度为v1,下落到高度为h2的B处时速度为v2,重力加速度为g,不计空气阻力,选择地面为参考平面.
(1)求从A至B的过程中重力做的功;
重点探究
图3
一、对机械能守恒定律的理解
答案 W=mgΔh=mg(h1-h2)=mgh1-mgh2 ①
(2)求物体在A、B处的机械能EA、EB;
(3)比较物体在A、B处的机械能的大小.
即EB=EA.
1.对机械能守恒条件的理解
(1)只有重力做功,只发生动能和重力势能的相互转化.
(2)只有弹力做功,只发生动能和弹性势能的相互转化.
(3)只有重力和弹力做功,发生动能、弹性势能、重力势能的相互转化.
(4)除受重力或弹力外,其他力也做功,但其他力做功的代数和始终为零.
知识深化
2.判断机械能是否守恒的方法
(1)做功条件分析:只有重力和系统内弹力做功,其他力不做功或做功的代数和始终为零.
(2)能量转化分析:系统内只有动能、重力势能及弹性势能的相互转化,即系统内只有物体间的机械能相互转移,则机械能守恒.
(3)定义判断法:如物体沿竖直方向或沿斜面匀速运动时,动能不变,势能变化,机械能不守恒.
例1 如图4所示,下列关于机械能是否守恒的判断正确的是
A.甲图中,物体A将弹簧压缩的过程中,
A机械能守恒
B.乙图中,A置于光滑水平面,物体B沿
光滑斜面下滑,物体B机械能守恒
C.丙图中,不计任何阻力时A加速下落、
B加速上升过程中,A、B系统机械能守恒
D.丁图中,系在橡皮条一端的小球向下摆动时,小球的机械能守恒
图4
√
解析 若不计空气阻力,题图甲中重力和弹力做功,物体A和弹簧组成的系统机械能守恒,但物体A机械能不守恒,选项A错误;
题图乙中物体B除受重力外,还受弹力,弹力对B做负功,机械能不守恒,但A、B组成的系统机械能守恒,选项B错误;
题图丙中绳子张力对A做负功,对B做正功,代数和为零,A、B系统机械能守恒,选项C正确;
题图丁中小球的重力势能转化为小球的动能和橡皮条的弹性势能,小球的机械能不守恒,选项D错误.
针对训练1 (2019·福建宁德六市高一期中联考)在下列情况中,机械能守恒的是
A.飘落的树叶
B.沿着斜面匀速下滑的物体
C.被起重机匀加速吊起的物体
D.不计空气阻力,推出的铅球在空中运动的过程
√
解析 树叶在飘落过程中,空气阻力做负功,机械能减少,故A错误;
沿着斜面匀速下滑的物体,摩擦力做功,故机械能不守恒,故B错误;
物体被起重机匀加速吊起时拉力对物体做功,故物体的机械能不守恒,故C错误;
推出的铅球在空中运动且不计空气阻力,只有重力做功,机械能守恒,故D正确.
例2 (多选)如图5,一根轻弹簧下端固定,竖立在水平面上.其上方A位置有一小球,小球从静止开始下落到B位置接触弹簧的上端,在C位置小球所受弹力大小等于重力,在D位置小球速度减小到零.不计空气阻力,则小球
A.下落至C处速度最大
B.由A至D的过程中机械能守恒
C.由B至D的过程中,动能先增大后减小
D.由A运动到D时,重力势能的减少量等于弹簧弹性势能的
增加量
√
图5
√
√
解析 小球从B至C过程,重力大于弹力,合力向下,小球做加速运动,小球从C至D过程,重力小于弹力,合力向上,小球做减速运动,所以动能先增大后减小,在C点动能最大,速度最大,故A、C正确;
由A至B下落过程中小球只受重力,其机械能守恒,从B→D过程,小球和弹簧组成的系统机械能守恒,但小球的机械能不守恒,故B错误;
在D位置小球速度减小到零,小球的动能为零,则从A运动到D时,小球重力势能的减少量等于弹簧弹性势能的增加量,故D正确.
二、机械能守恒定律的应用
1.机械能守恒定律常用的三种表达式
(1)从不同状态看:Ek1+Ep1=Ek2+Ep2(或E1=E2)
此式表示系统两个状态的机械能总量相等.
(2)从能的转化角度看:ΔEk=-ΔEp
此式表示系统动能的增加(减少)量等于势能的减少(增加)量.
(3)从能的转移角度看:ΔEA增=ΔEB减
此式表示系统A部分机械能的增加量等于系统剩余部分,即B部分机械能的减少量.
2.应用机械能守恒定律解题的一般步骤
(1)根据题意选取研究对象;
(2)明确研究对象的运动过程,分析研究对象在此过程中的受力情况,弄清各力做功的情况,判断机械能是否守恒.
(3)恰当地选取参考平面,确定研究对象在此过程中的初态和末态的机械能.
(4)根据机械能守恒定律的不同表达式列方程并求解.
例3 (2019·大庆中学高一期末)一条长为0.80 m的轻绳一端固定在O点,另一端连接一质量m=0.10 kg的小球,悬点O距离水平地面的高度H=1.00 m,开始时小球处于A点,此时轻绳拉直处于水平方向上,如图6所示,让小球从静止释放,当小球运动到B点时,轻绳碰到悬点O正下方一个固定的光滑小钉子P时立刻断裂,不计轻绳断裂的能量损失,取重力加速度g=10 m/s2,不计空气阻力,求:
(1)当小球运动到B点时的速度大小;
图6
答案 4.0 m/s
解析 设小球运动到B点时的速度大小为vB,
(2)绳断裂后球从B点抛出并落在水平地面的C点,求小球落到C点时的瞬时速度的大小.
解析 小球从B点做平抛运动,小球只受重力,全过程机械能守恒,
针对训练2 如图7所示,质量m=50 kg的跳水运动员从距水面高h=10 m的跳台上以v0=5 m/s的速度斜向上起跳,最终落入水中,若忽略运动员的身高,取g=10 m/s2,不计空气阻力.求:
(1)运动员在跳台上时具有的重力势能(以水面为参考平面);
图7
答案 5 000 J
解析 以水面为参考平面,则运动员在跳台上时具有的重力势能为
Ep=mgh=5 000 J.
(2)运动员起跳时的动能;
答案 625 J
解析 运动员起跳时的速度为v0=5 m/s,
则运动员起跳时的动能为
(3)运动员入水时的速度大小;入水时的速度大小与起跳时的方向有关吗?
答案 15 m/s 无关
解析 运动员从起跳到入水过程中,只有重力做功,运动员的机械能守恒,
此速度大小与起跳时的方向无关.
1.(机械能守恒的判断)(2019·泉州市高一下月考)下列说法中正确的是
A.图8甲中“蛟龙号”被吊车匀速吊
下水的过程中它的机械能守恒
B.图乙中物块在恒力F作用下沿固定
光滑斜面匀速上滑过程中,物块的
机械能守恒
C.图丙中物块沿固定斜面匀速下滑过程中,物块的机械能不守恒
D.图丁中撑竿跳高运动员在上升过程中机械能守恒
1
2
3
4
随堂演练
√
图8
解析 题图甲中“蛟龙号”被吊车匀速吊下水的过程中,动能不变,重力势能变小,所以机械能不守恒,故A错误;
题图乙中物块在恒力F作用下沿固定光滑斜面匀速上滑过程中,恒力F做正功,物块的机械能增加,故B错误;
题图丙中物块沿固定斜面匀速下滑过程中,物块在斜面上受力平衡,重力沿斜面向下的分力与摩擦力平衡,摩擦力做负功,物块的机械能减小,故C正确;
题图丁中撑竿跳高运动员在上升过程中,撑竿的弹性势能转化为运动员的机械能,所以运动员的机械能不守恒,故D错误.
1
2
3
4
2.(机械能守恒定律的应用)以相同大小的初速度v0将物体从同一水平面分别竖直上抛、斜上抛、沿光滑斜面(足够长)上滑,如图9所示,三种情况达到的最大高度分别为h1、h2和h3,不计空气阻力,则
A.h1=h2>h3
B.h1=h2<h3
C.h1=h3<h2
D.h1=h3>h2
1
2
3
4
√
图9
解析 竖直上抛的物体和沿光滑斜面运动的物体,上升到最高点时,速度均为0,
斜上抛的物体在最高点速度不为零,设为v1,
1
2
3
4
3.(机械能守恒定律的应用)如图10所示,由距离地面h2=1 m的高度处以v0=4 m/s的速度斜向上抛出质量为m=1 kg的物体,当其上升的高度为h1=0.4 m时到达最高点,最终落在水平地面上,现以过抛出点的水平面为参考平面,取重力加速度g=10 m/s2,不计空气阻力,则
A.物体在最大高度处的重力势能为14 J
B.物体在最大高度处的机械能为16 J
C.物体落地前瞬间的机械能为8 J
D.物体落地前瞬间的动能为8 J
1
2
3
4
√
图10
解析 物体在最高点时具有的重力势能Ep1=mgh1=1×10×0.4 J=4 J,A错误;
物体在最高点时具有的机械能等于刚抛出时的动能,即8 J,B错误;
物体在下落过程中机械能守恒,落地前在任意位置的机械能都等于8 J,C正确;
物体落地前瞬间的动能Ek=E-Ep2=E-mgh2=8 J-1×10×(-1) J=18 J,D错误.
1
2
3
4
(1)求小球在B、A两点的动能之比;
1
2
3
4
图11
答案 5∶1
解析 设小球的质量为m,小球在A点的动能为EkA,
1
2
3
4
由①②式得EkB∶EkA=5∶1 ③
(2)通过计算判断小球能否沿轨道运动到C点.
1
2
3
4
答案 见解析
解析 若小球能沿轨道运动到C点,
则小球在C点所受轨道的正压力FN应满足FN≥0 ④
设小球在C点的速度大小为vC,由牛顿第二定律有
1
2
3
4
1
2
3
4
故小球恰好可以沿轨道运动到C点.
考点一 机械能守恒的判断
1.(2019·重庆市江津中学、合川中学等七校高一下学期期末)下列描述中,机械能守恒的是
A.沿斜面匀速向上行驶的汽车
B.被匀速向上吊起的集装箱
C.在真空中水平抛出的石块
D.物体以 g的加速度竖直向上做匀减速运动
基础对点练
课时对点练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
2.(2019·上饶市玉山一中高一下期中)关于机械能守恒的叙述,下列说法正确的是
A.做匀速圆周运动的物体,机械能一定守恒
B.物体所受的合力不等于零,机械能可能守恒
C.物体做匀速直线运动,机械能一定守恒
D.物体所受合力做功为零,机械能一定守恒
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
解析 若物体在竖直平面内做匀速圆周运动,动能不变,重力势能变化,机械能不守恒,故A错误;
物体所受的合力不等于零,它的机械能可能守恒,例如物体做自由落体运动,故B正确;
物体在竖直方向做匀速直线运动时,动能不变,重力势能变化,机械能不守恒,故C错误;
物体所受合力做功为零,它的动能不变,重力势能可能变化,机械能不一定守恒,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3.(多选)如图1所示,细绳的一端固定于O点,另一端系一小球,在O点的正下方钉一个钉子C.小球从一定高度处释放,不计一切阻力,细绳摆到竖直位置时,被钉子挡住,比较细绳被钉子挡住前、后瞬间
A.小球的动能变小
B.小球的动能不变
C.小球的重力势能变小
D.小球的机械能不变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
√
图1
解析 小球到达最低点时,速度方向沿水平方向,在钉子挡住细绳瞬间,合外力对小球做功为零,则小球的动能不变,故A错误,B正确;
在钉子挡住细绳瞬间,小球的质量和高度不变,则小球的重力势能不变,故C错误;
在钉子挡住细绳瞬间,小球的动能与重力势能都不变,则小球的机械能不变,故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4.(多选)(2019·三明市高一下学期期末)如图2所示,一轻弹簧一端固定于O点,另一端系一重物,将重物从与悬点O在同一水平面且弹簧保持原长的A点无初速度释放,让它自由摆下,不计空气阻力,在重物由A点摆到最低点的过程中
A.重物的机械能减少
B.重物与弹簧组成的系统的机械能不变
C.重物与弹簧组成的系统的机械能增加
D.重物与弹簧组成的系统的机械能减少
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
图2
√
解析 重物自由摆下的过程中,弹簧拉力对重物做负功,重物的机械能减少,选项A正确;
对重物与弹簧组成的系统而言,除重力、弹力外,无其他外力做功,故系统的机械能守恒,选项B正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
考点二 机械能守恒定律的应用
5.(2019·天津市第一中学高一下期中)如图3,在地面上以初速度v0抛出质量为m的物体,抛出后物体落在比地面低h的海平面上,重力加速度为g,若以地面为参考平面,且不计空气阻力,则
A.物体在海平面上的重力势能为mgh
B.重力对物体做的功为-mgh
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
图3
解析 以地面为参考平面,海平面低于地面的高度为h,所以物体在海平面上时的重力势能为-mgh,故A错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
重力做功与路径无关,与初、末位置的高度差有关,抛出点与海平面的高度差为h,并且重力做正功,所以整个过程重力对物体做功为mgh,故B错误;
6.(多选)(2019·江西萍乡高一下期中)如图所示,A、B、C、D四个图中的小球完全相同.现从同一高度h处由静止释放小球,小球下落同样的高度,然后进入不同的轨道.A图中的轨道是一个内径略大于小球直径的管,其上部为直管,下部为圆弧形,底端与斜面平滑衔接,管的高度高于h;B图中的轨道是半圆轨道,其直径等于h;C图中的轨道高度低于h;D图中的轨道是一段斜面,且高于h.如果不计任何阻力和拐弯处的能量损失,小球进入轨道后不能运动到h高度的图是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
√
解析 A中小球离开轨道后做竖直上抛运动,运动到最高点时的速度为零,根据机械能守恒定律得mgh+0=mgh′+0,则h=h′,故能运动到h高度;
B中小球在内轨道运动,假设小球能通过圆轨道最高点,则小球通过最高点的最小速度为v= ,故小球在最高点的速度不为零,根据机械能守恒定律可知假设不成立,故小球不能运动到h高度;
C中小球离开轨道后做斜抛运动,水平方向做匀速直线运动,运动到最高点时在水平方向上有速度,即在最高点的速度不为零,根据机械能守恒定律可知,小球不能运动到h高度;
D中小球到达右侧斜面上最高点时的速度为零,根据机械能守恒定律得mgh+0=mgh′+0,则h=h′,故能运动到h高度.故选B、C.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7.(2019·北京市十一学校高一下期末)如图4所示,轻弹簧置于光滑水平面上,一端固定在竖直墙壁,另一端自由伸长.现分别用质量不相等的两物块将弹簧压缩相同长度后由静止释放,物块离开弹簧的瞬间
A.质量小的速度大
B.质量小的动能大
C.质量大的速度大
D.质量大的动能大
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
图4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8.(多选)质量相同的小球A和B分别悬挂在长为L和2L的不同长绳上,先将小球A、B拉至同一水平高度(如图5所示)从静止释放,当两绳竖直时,不计空气阻力,则
A.两球的速率一样大
B.两球的动能一样大
C.两球的机械能一样大
D.两球所受的拉力一样大
√
图5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
解析 两球在下落过程中机械能守恒,开始下落时,重力势能相等,动能都为零,所以机械能相等,下落到最低点时的机械能也一样大,选项C正确;
以小球A为研究对象,设小球到达最低点时的速度大小为vA,动能为EkA,小球所受的拉力大小为FA,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9.(多选)(2019·平顶山市高一下学期期末)蹦极是一项有趣的极限运动,轻质弹性绳的一端固定,另一端和运动员相连,运动员经一段自由下落后绳被拉直,绳的形变是弹性形变,绳处于原长时的弹性势能为零.则在运动员从静止开始自由下落,直至最低点的过程中,下列表述正确的是(整个过程中空气阻力不计)
A.运动员的机械能守恒
B.弹性绳的弹性势能先增大后减小
C.运动员与弹性绳的总机械能守恒
D.运动员动能最大时弹性绳的弹性势能不为零
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
解析 运动员开始自由下落,从弹性绳开始伸直到最低点的过程中,先是拉力增加但仍小于重力,合外力向下,运动员向下做加速度减小的加速运动,当加速度为零时,速度最大,动能最大,此后拉力大于重力且拉力继续增加,合外力向上,运动员开始做加速度增大的减速运动,速度减小,动能减小,所以运动员的机械能不守恒,但运动员与弹性绳的总机械能守恒,故A错误,C正确;
运动员开始自由下落,弹性绳的弹性势能不变,从弹性绳开始伸直到最低点的过程中,弹性绳的弹性势能增大,故B错误;
当加速度为零时,速度最大,动能最大,弹性绳的弹力等于运动员的重力,弹性绳的弹性势能不为零,故D正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10.(2019·大庆中学高一期末)一个小石子从高为10 m处自由下落,不计空气阻力,经一段时间后小石子的动能恰等于它的重力势能(以地面为参考平面),g=10 m/s2,则该时刻小石子的速度大小为
A.5 m/s B.10 m/s C.15 m/s D.20 m/s
1
2
3
4
5
6
7
8
9
10
11
12
13
14
√
15
能力综合练
解析 运动的过程中小石子的机械能守恒,
设小石子在离地高度为h′时动能等于重力势能,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
11.(多选)(2019·西安高级中学期末)一个物体以一定的初速度竖直上抛,不计空气阻力,如图所示为表示物体的动能Ek随高度h变化的图像A、物体的重力势能Ep随速度v变化的图像B(图线形状为四分之一圆弧)、物体的机械能E随高度h变化的图像C、物体的动能Ek随速度v变化的图像D(图线为开口向上的抛物线的一部分),其中可能正确的是
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
√
√
√
解析 设物体的初速度为v0,物体的质量为m,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
则Ep-v图像为开口向下的抛物线(第一象限中的部分),图像B错误;
由于竖直上抛运动过程中机械能守恒,所以E-h图像为一平行于h轴的直线,图像C可能正确;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12.如图6所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态,现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),重力加速度为g,则在圆环下滑到最大距离的过程中
A.圆环的机械能守恒
B.弹簧弹性势能增加了 mgL
C.圆环下滑到最大距离时,所受合力为零
D.圆环重力势能与弹簧弹性势能之和始终保持不变
√
图6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解析 圆环在下落过程中机械能减少,弹簧弹性势能增加,圆环与弹簧组成的系统机械能守恒,圆环下落到最低点时速度为零,但是加速度不为零,即合力不为零;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
圆环下落过程中重力势能、动能及弹簧弹性势能之和保持不变,故选B.
13.(多选)(2019·西安二十六中期末)如图7所示,细轻杆的一端与质量为m的小球相连,可绕O点的水平轴自由转动.现给小球一初速度,使它在竖直平面内做圆周运动,a、b分别表示轨道的最低点和最高点,重力加速度为g,则小球在这两点对杆的作用力大小之差可能为
A.3mg
B.4mg
C.5mg
D.6mg
1
2
3
4
5
6
7
8
9
10
11
12
13
14
图7
√
15
√
√
解析 小球运动到b点时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
对杆和球组成的系统,由b→a机械能守恒,
vb=0时,ΔF=4mg,若vb增大,则ΔF增大;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
此时ΔF=6mg
则ΔF=6mg
综上,A错误,B、C、D正确.
14.图8是某轻轨车站的设计方案,与站台连接的轨道有一个小坡度,电车进站要上坡,出站要下坡.已知坡高为2 m,电车到a点时的速度为25.2 km/h,此后便切断电车的电源,如果不考虑电车所受的摩擦力,电车能否冲上站台?如果电车不能冲上站台,请说明理由;如果电车能冲上站台,求它到达b点时的速度大小.(g取10 m/s2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
图8
15
答案 能 3 m/s
解析 电车电源被切断后,只有重力做功,故机械能守恒.
其中v1=25.2 km/h=7 m/s
若这些动能全部转化为重力势能,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
设电车到达b点时的速度为v2,由机械能守恒定律得
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15.(2019·山师大附中高一下学期期末)如图9是一个设计“过山车”的试验装置的原理示意图,斜面AB与竖直面内的圆形轨道在B点平滑连接,斜面AB和圆形轨道都是光滑的,圆形轨道半径为R,一个质量为m的小车(可视为质点)在A点由静止释放沿斜面滑下,小车恰能通过圆形轨道的最高点C.已知重力加速度为g.求:
(1)A点距水平面的高度h;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案 2.5R
图9
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
由A运动到C,根据机械能守恒定律得:
解得:h=2.5R
(2)运动到B点时小车对圆形轨道压力的大小.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案 6mg
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
解得:FN=6mg
由牛顿第三定律可知,运动到B点时小车对圆形轨道的压力大小为6mg.
