人教版数学八年级下册18.1 平行四边形性质与判定同步练习卷(Word版 含答案)
文档属性
| 名称 | 人教版数学八年级下册18.1 平行四边形性质与判定同步练习卷(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 18:38:59 | ||
图片预览




文档简介
人教版数学八年级下册《平行四边形性质与判定》
同步基础练习卷
一、选择题
1.平行四边形ABCD中,如果∠B=100°,那么∠A、∠D的值分别是( )
A.∠A=80°,∠D=100° B.∠A=100°,∠D=80°
C.∠B=80°,∠D=80° D.∠A=100°,∠D=100°
2.已知□ABCD的两条对角线AC=18,BD=8,则BC的长度可能为( )
A.5?????? B.10??? ? C.13?? ?? D.26
3.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为( ).
A.4,4,8,8 B.5,5,7,7 C.5.5,5.5,6.5,6.5 D.3,3,9,9
4.若平行四边形ABCD的周长为28,△ABC的周长为17cm,则AC的长为 ( )
A.11cm B. 5.5cm C.4cm D.3cm
5.如图,?ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO周长是(??? )
A.10? B.14? C.20? D.22
6.如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为10,则?ABCD的周长为( )
A.14 B.16 C.20 D.18
7.如图,在?ABCD中,AD=16,点E,F分别是BD,CD的中点,则EF等于( )
A.10 B.8 C.6 D.4
8.如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
A.S1+S2=S3+S4 B.S1+S2>S3+S4 C.S1+S3=S2+S4 D.S1+S2<S3+S4
9.如图,平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于( )
A.20° B.25° C.30° D.35°
10.如图,E为?ABCD外一点,且EB⊥BC,ED⊥CD,若∠E=65°,则∠A的度数为( )
A.65° B.100° C.115° D.135°
11.如图,在□ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,□ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.4
12.如图,□ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16 B.14 C.12 D.10
二 、填空题
13.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,图中全等三角形共有________对
14.如图,加一个条件 与∠A+∠B=180°能使四边形ABCD成为平行四边形.
15.E为□ABCD边AD上一点,将ABE沿BE翻折得到FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE=______
16.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.
17.如图,E,F是?ABCD对角线BD上的两点,请你添加一个适当的条件: ?? ,使四边形AECF是平行四边形.
18.一个四边形四条边顺次是a、b、c、d,且a2+b2+c2+d2=2ac+2bd,则这个四边形是_______
三 、解答题
19.如图,已知△ABC中,D为AB的中点.
(1)请用尺规作图法作边AC的中点E,并连结DE(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若DE=4,求BC的长.
20.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24,△OAB的周长是18,试求EF的长.
21.如图,已知:在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,点E,F分别是边BC,AC的中点.求证:DF=BE.
22.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB。
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形。
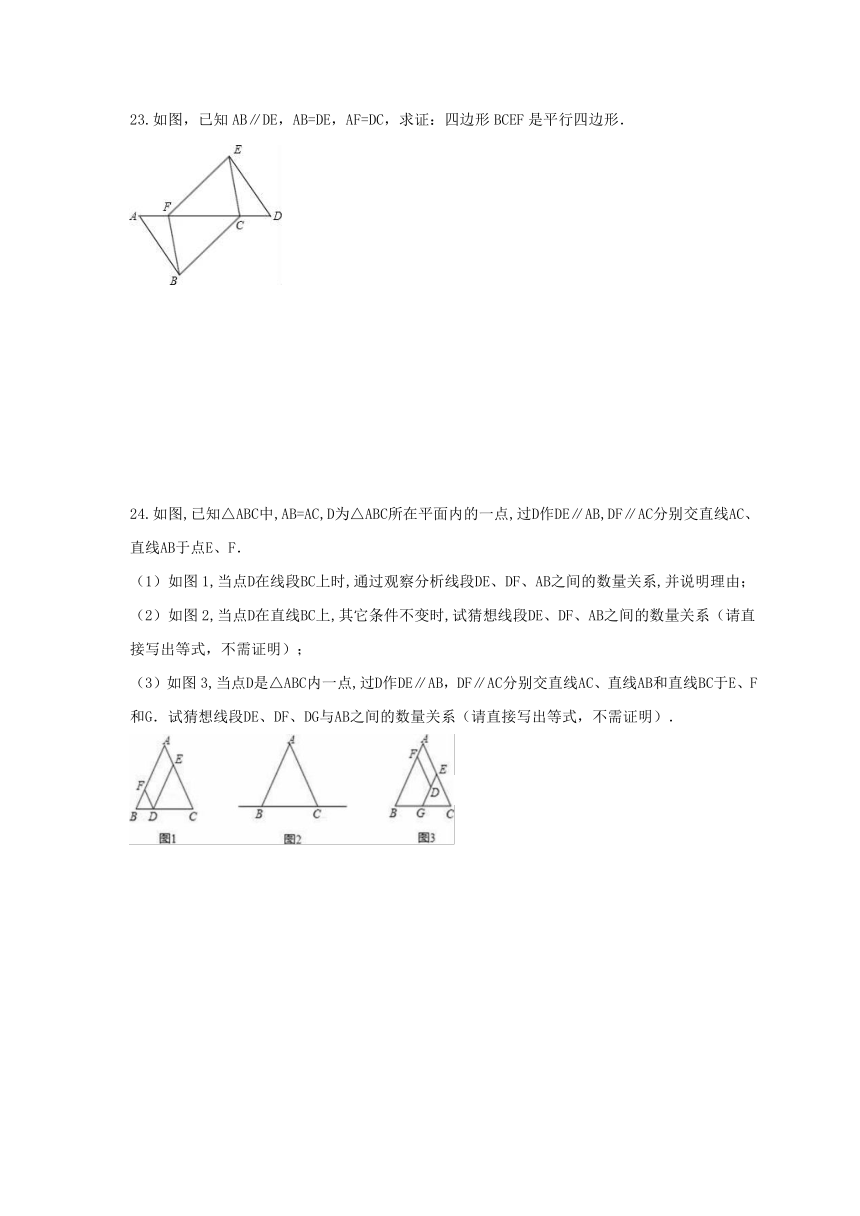
23.如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.
24.如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC、直线AB于点E、F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其它条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC、直线AB和直线BC于E、F和G.试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).
25.如图,已知△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED.
参考答案
1.A
2.B.
3.B
4.D
5.B.
6.C.
7.B.
8.C
9.A.
10.C
11.C
12.C
13.答案为:4;
14.答案为:AD=BC或AB∥CD.
15.答案为:51
16.答案为:3;
17.答案为:BE=DF或BF=DE或∠BAE=∠DCF
18.答案为:平行四边形
19.解:(1)作线段AC的垂直平分线MN交AC于E,点E就是所求的点.
(2)∵AD=DB,AE=EC,
∴DE∥BC,DE=BC,
∵DE=4,
∴BC=8.
20.解:∵四边形ABCD是平行四边形∴AO=CO,BO=DO,
∵AC+BD=24,∴AO+BO=12,
∵△OAB的周长是18,∴AB=18﹣(AO+BO)=18﹣12=6,
∵点E,F分别是线段AO,BO的中点∴EF=3.
21.证明:
∵∠BAC=90°,
∴∠DAF=90°,
∵点E,F分别是边BC,AC的中点,
∴AF=FC,BE=EC,FE是△ABC的中位线,
∴FE=AB,FE∥AB,
∴∠EFC=∠BAC=90°,
∴∠DAF=∠EFC,
∵AD=AB,
∴AD=FE,
在△ADF和△FEC中,,∴△ADF≌△FEC(SAS),
∴DF=EC,
∴DF=BE.
22.解:(1)∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD-∠BAD=∠BAC-∠BAD,即:∠EAB=∠DAC,
∴△ABE≌△ACD(SAS);
(2)证明:∵△ABE≌△ACD,∴BE=DC,∠EBA=∠DCA,
又∵BF=DC,∴BE=BF.
∵△ABC是等边三角形,∴∠DCA=60°,
∴△BEF为等边三角形.∴∠EFB=60°,EF=BF
∵△ABC是等边三角形,∴∠ABC=60°,
∴∠ABC=∠EFB,∴EF∥BC,即EF∥DC,
∵EF=BF,BF=DC,∴EF=DC,
∴四边形EFCD是平行四边形。
23.证明:连接AE、DB、BE,BE交AD于点O,
∵ABDE,∴四边形ABDE是平行四边形,∴OB=OE,OA=OD,
∵AF=DC,∴OF=OC,∴四边形BCEF是平行四边形.
24.解:(1)DE+DF=AB.理由如下:
如图1.∵DE∥AB,DF∥AC,∴四边形AEDF是平行四边形,∴DE=AF.
∵DF∥AC,∴∠FDB=∠C,∵AB=AC,∴∠C=∠B,∴∠FDB=∠B,
∴DF=FB,∴DE+DF=AF+FB=AB;
(2)当点D在直线BC上时,分三种情况:
①当点D在CB延长线上时,如图2①,AB=DE﹣DF;
②当点D在线段BC上时,如图1,AB=DE+DF;
③当点D在BC的延长线上时,如图2②,AB=DF﹣DE;
(3)如图3,AB=DE+DG+DF.
25.解:延长BE交AC于F,
∵AE平分∠BAC作业帮,BE⊥AE,
∴△BAF是等腰三角形,
∴BE=EF,AB=AF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC-AF=7-5=2,
∵D为BC中点
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=0.5CF=1.
同步基础练习卷
一、选择题
1.平行四边形ABCD中,如果∠B=100°,那么∠A、∠D的值分别是( )
A.∠A=80°,∠D=100° B.∠A=100°,∠D=80°
C.∠B=80°,∠D=80° D.∠A=100°,∠D=100°
2.已知□ABCD的两条对角线AC=18,BD=8,则BC的长度可能为( )
A.5?????? B.10??? ? C.13?? ?? D.26
3.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为( ).
A.4,4,8,8 B.5,5,7,7 C.5.5,5.5,6.5,6.5 D.3,3,9,9
4.若平行四边形ABCD的周长为28,△ABC的周长为17cm,则AC的长为 ( )
A.11cm B. 5.5cm C.4cm D.3cm
5.如图,?ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO周长是(??? )
A.10? B.14? C.20? D.22
6.如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E,若△CDE的周长为10,则?ABCD的周长为( )
A.14 B.16 C.20 D.18
7.如图,在?ABCD中,AD=16,点E,F分别是BD,CD的中点,则EF等于( )
A.10 B.8 C.6 D.4
8.如图,平行四边形ABCD中,P是形内任意一点,△ABP,△BCP,△CDP,△ADP的面积分别为S1,S2,S3,S4,则一定成立的是( )
A.S1+S2=S3+S4 B.S1+S2>S3+S4 C.S1+S3=S2+S4 D.S1+S2<S3+S4
9.如图,平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于( )
A.20° B.25° C.30° D.35°
10.如图,E为?ABCD外一点,且EB⊥BC,ED⊥CD,若∠E=65°,则∠A的度数为( )
A.65° B.100° C.115° D.135°
11.如图,在□ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,□ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.4
12.如图,□ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )
A.16 B.14 C.12 D.10
二 、填空题
13.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,图中全等三角形共有________对
14.如图,加一个条件 与∠A+∠B=180°能使四边形ABCD成为平行四边形.
15.E为□ABCD边AD上一点,将ABE沿BE翻折得到FBE,点F在BD上,且EF=DF.若∠C=52°,则∠ABE=______
16.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.
17.如图,E,F是?ABCD对角线BD上的两点,请你添加一个适当的条件: ?? ,使四边形AECF是平行四边形.
18.一个四边形四条边顺次是a、b、c、d,且a2+b2+c2+d2=2ac+2bd,则这个四边形是_______
三 、解答题
19.如图,已知△ABC中,D为AB的中点.
(1)请用尺规作图法作边AC的中点E,并连结DE(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,若DE=4,求BC的长.
20.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24,△OAB的周长是18,试求EF的长.
21.如图,已知:在△ABC中,∠BAC=90°,延长BA到点D,使AD=AB,点E,F分别是边BC,AC的中点.求证:DF=BE.
22.如图,△ABC和△ADE都是等边三角形,点D在BC边上,AB边上有一点F,且BF=DC,连接EF、EB。
(1)求证:△ABE≌△ACD;
(2)求证:四边形EFCD是平行四边形。
23.如图,已知AB∥DE,AB=DE,AF=DC,求证:四边形BCEF是平行四边形.
24.如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC、直线AB于点E、F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其它条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC、直线AB和直线BC于E、F和G.试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).
25.如图,已知△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E点,若AB=5,AC=7,求ED.
参考答案
1.A
2.B.
3.B
4.D
5.B.
6.C.
7.B.
8.C
9.A.
10.C
11.C
12.C
13.答案为:4;
14.答案为:AD=BC或AB∥CD.
15.答案为:51
16.答案为:3;
17.答案为:BE=DF或BF=DE或∠BAE=∠DCF
18.答案为:平行四边形
19.解:(1)作线段AC的垂直平分线MN交AC于E,点E就是所求的点.
(2)∵AD=DB,AE=EC,
∴DE∥BC,DE=BC,
∵DE=4,
∴BC=8.
20.解:∵四边形ABCD是平行四边形∴AO=CO,BO=DO,
∵AC+BD=24,∴AO+BO=12,
∵△OAB的周长是18,∴AB=18﹣(AO+BO)=18﹣12=6,
∵点E,F分别是线段AO,BO的中点∴EF=3.
21.证明:
∵∠BAC=90°,
∴∠DAF=90°,
∵点E,F分别是边BC,AC的中点,
∴AF=FC,BE=EC,FE是△ABC的中位线,
∴FE=AB,FE∥AB,
∴∠EFC=∠BAC=90°,
∴∠DAF=∠EFC,
∵AD=AB,
∴AD=FE,
在△ADF和△FEC中,,∴△ADF≌△FEC(SAS),
∴DF=EC,
∴DF=BE.
22.解:(1)∵△ABC和△ADE都是等边三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=60°,
∴∠EAD-∠BAD=∠BAC-∠BAD,即:∠EAB=∠DAC,
∴△ABE≌△ACD(SAS);
(2)证明:∵△ABE≌△ACD,∴BE=DC,∠EBA=∠DCA,
又∵BF=DC,∴BE=BF.
∵△ABC是等边三角形,∴∠DCA=60°,
∴△BEF为等边三角形.∴∠EFB=60°,EF=BF
∵△ABC是等边三角形,∴∠ABC=60°,
∴∠ABC=∠EFB,∴EF∥BC,即EF∥DC,
∵EF=BF,BF=DC,∴EF=DC,
∴四边形EFCD是平行四边形。
23.证明:连接AE、DB、BE,BE交AD于点O,
∵ABDE,∴四边形ABDE是平行四边形,∴OB=OE,OA=OD,
∵AF=DC,∴OF=OC,∴四边形BCEF是平行四边形.
24.解:(1)DE+DF=AB.理由如下:
如图1.∵DE∥AB,DF∥AC,∴四边形AEDF是平行四边形,∴DE=AF.
∵DF∥AC,∴∠FDB=∠C,∵AB=AC,∴∠C=∠B,∴∠FDB=∠B,
∴DF=FB,∴DE+DF=AF+FB=AB;
(2)当点D在直线BC上时,分三种情况:
①当点D在CB延长线上时,如图2①,AB=DE﹣DF;
②当点D在线段BC上时,如图1,AB=DE+DF;
③当点D在BC的延长线上时,如图2②,AB=DF﹣DE;
(3)如图3,AB=DE+DG+DF.
25.解:延长BE交AC于F,
∵AE平分∠BAC作业帮,BE⊥AE,
∴△BAF是等腰三角形,
∴BE=EF,AB=AF,
∵AB=5,
∴AF=5,
∵AC=7,
∴CF=AC-AF=7-5=2,
∵D为BC中点
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=0.5CF=1.
