7.1.2 平面直角坐标系 课件 (52张)
文档属性
| 名称 | 7.1.2 平面直角坐标系 课件 (52张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 00:00:00 | ||
图片预览









文档简介
(共52张PPT)
第七章
7.1.2
平面直角坐标系
人教版数学七年级下册
1.认识平面直角坐标系,了解点的坐标的意义.
2.会用坐标表示点,能画出点的坐标位.
学习目标
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2.反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了.
A
B
如何确定直线上点的位置?
1米
导入新知
1
知识点
平面直角坐标系
如何确定平面上点的位置呢?
合作探究
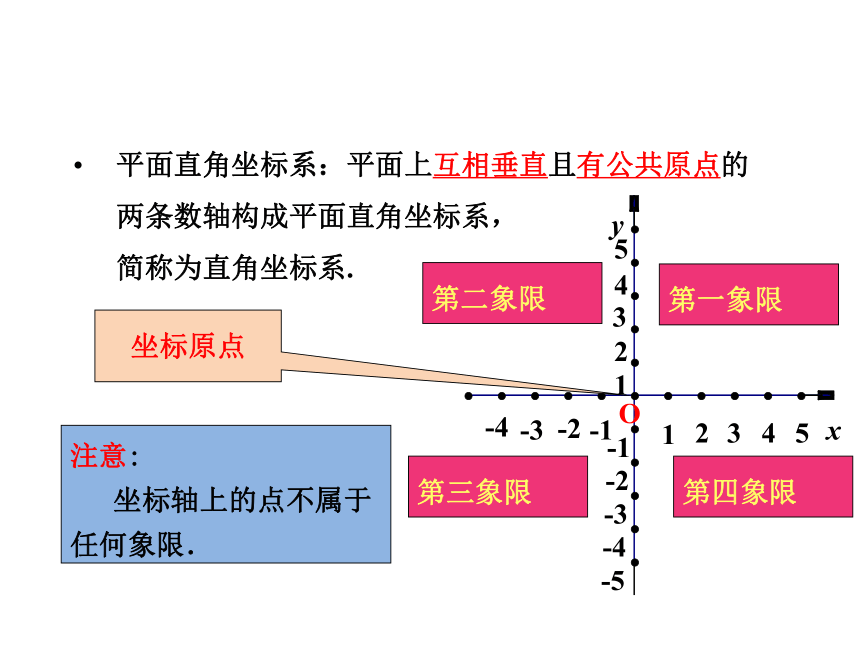
平面直角坐标系:平面上互相垂直且有公共原点的
两条数轴构成平面直角坐标系,
简称为直角坐标系.
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
坐标原点
注意:
坐标轴上的点不属于任何象限.
相关概念:
水平的数轴叫做x轴或横轴,习惯上取向右为正方
向;铅直的数轴叫做y轴或纵轴,取向上为正方向;
x轴和y轴统称坐标轴,它们的公共原点O称为平面
直角坐标系的原点.
下列语句不正确的是( )
A.平面直角坐标系中,两条互相垂直的数轴的交点是原点
B.平面直角坐标系所在的平面叫坐标平面
C.平面直角坐标系中x轴、y轴把坐标平面分成4部分
D.凡是两条互相垂直的直线都能组成平面直角坐标系
例1
D
导引:
本题主要考查平面直角坐标系的概念.根据平
面直角坐标系的概念可知A,B,C项正确.D
项不正确,因为平面直角坐标系必须由数轴构
成,且构成平面直角坐标系的两条数轴互相垂
直、原点重合.
本题应用定义法,要正确理解平面直角坐标系的
概念.
理解并认识平面直角坐标系必须明确:(1)建立平
面直角坐标系的平面叫坐标平面;(2)平面直角坐标系
必须具备:①由两条数轴组成;②这两条数轴有公共
原点且互相垂直.
新知小结
1
下列说法错误的是( )
A.平面内两条互相垂直的数轴就构成了平面直
角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每
个部分称为象限
D.坐标轴上的点不属于任何象限
A
巩固新知
2
知识点
平面直角坐标系内点的坐标
1、直角坐标系的横轴和纵轴将平面分成
____
部分,
从右上方的部分说起,按逆时针方向,各部分
依次是__________、
_________
、
_________
和__________.
2、坐标轴上的点属于哪一象限?
四
第一象限
第二象限
第三象限
第四象限
合作探究
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
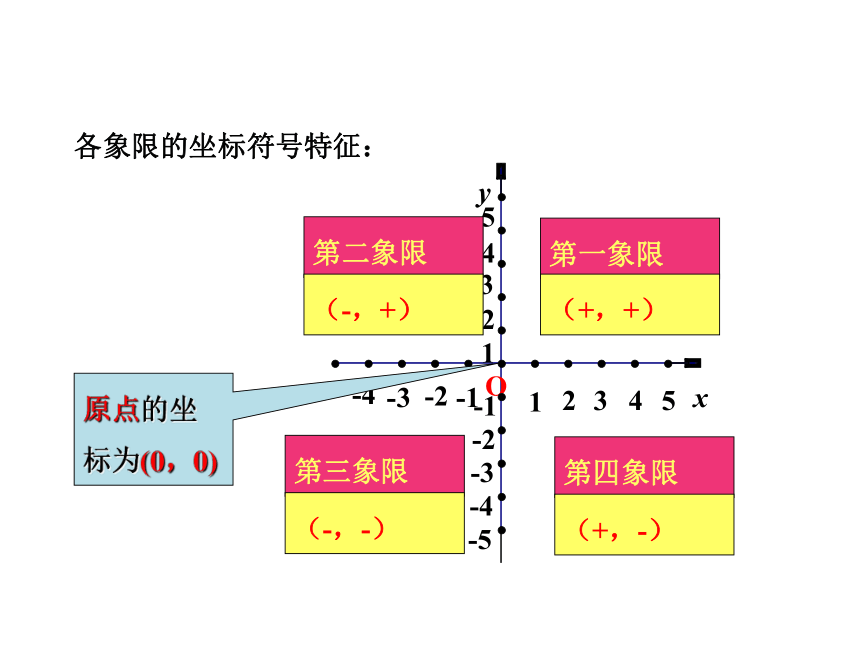
(+,+)
(-,+)
(-,-)
(+,-)
原点的坐标为(0,0)
各象限的坐标符号特征:
1、点P(x,y)在第一象限
x>0,y>0.
2、点P(x,y)在第二象限
x<0,y>0.
3、点P(x,y)在第三象限
x<0,y<0.
4、点P(x,y)在第四象限
x>0,y<0.
例在平面直角坐标系(如图)中描出下列各点:
A(4,5),
B(-2,3),
C(-4,-1),
D(2.5,-2),
E(0,-4).
例2
解:
如图,先在x轴上找出表示4的点,再在y轴上找出
表示5的点,过这两个点分别作x轴和y轴的垂线,
垂线的交点就是点A.
类似地,请你在图上
描出点B,C,D,E.
由点的坐标确定点的位置的方法:方法一是由点
的坐标的符号确定点的位置,即(+,+)的点在第一
象限,(-,+)的点在第二象限,(-,-)的点在第三
象限,(+,-)的点在第四象限;方法二是分别过两
坐标轴上表示该点的坐标的点作两坐标轴的垂线,这
两条垂线的交点位置即为该点的位置.
新知小结
1
写出图中点A,B,C,D,E,F的坐标.
解:
A点的坐标为(-2,-2),
B点的坐标为(-5,4),
C点的坐标为(5,-4),D点的坐标为(0,-3),
E点的坐标为(2,5),F点的坐标为(-3,0).
巩固新知
2
下列说法错误的是( )
A.象限内的点的坐标可用一个有序数对来表示
B.坐标轴上的点的坐标可用一个有序数对来表
示
C.过点P向x轴作垂线,点P与垂足之间的线段
长是点P的纵坐标
D.过点P向y轴作垂线,点P与垂足之间的线段
长不一定是点P的横坐标
C
3
【中考·荆门】在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
4
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
A.(-3,300)
B.(7,-500)
C.(9,600)
D.(-2,-800)
C
3
知识点
点的位置与点的坐标的关系
点M(x,y)所处的位置
坐标特征
在x轴正半轴上:M(正,0)
在x轴负半轴上:M(负,0)
在y轴正半轴上:M(0,正)
在y轴负半轴上:M(0,负)
坐标轴上的点的坐标:
点M在x轴上
点M在y轴上
合作探究
拓展:
平行于x轴的直线上的点的纵坐标相等;
平行于y轴的直线上的点的横坐标相等.
例3
已知点P(x+6,x-4)在y轴上,则点P
的坐标是__________.
导引:根据y轴上点的坐标的特征可得x+6=
0,得x=-6,所以x-4=-10.故点P
的坐标是(0,-10).
(0,-10)
1
【中考·台湾】如图为A,B,C三点在坐标平面上的位置图.若A,B,C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
A.5
B.3
C.-3
D.-5
B
巩固新知
平面直角坐标系的三要素:
(1)两条数轴;
(2)互相告直;
(3)公共原点.
1
知识小结
归纳新知
2.
第一、二、三、四象限内点的坐标的符号依次
为(+,+),(-,+),(-,-),(+,-).
3.x轴上的点纵坐标为0,y轴上的点横坐标为0.
4.
建立坐标系常用的方法有:
(1)以图形上的某已知点或线段的中点为原点;
(2)以图形上某线段所在直线为x
轴(或y
轴);
(3)利用图形的轴对称性以对称轴为x
轴(或y
轴).
若点P(a,b)在第二象限,则点M(b-a,a-b)
在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
2
易错小结
易错点:对直角坐标系内的点的坐标的符号理解不清
而致错.
A或B或C
错解:
错解产生的原因有两个:一是对各象限内点的坐标特点没有掌握好,二是没有弄清b-a与a-b的符号.
诊断:
根据各象限内的点的坐标的符号特点,先判定a与b的符号,再确定b-a与a-b的符号.
解题策略:
原点重合
平面直角坐标系
x轴或横轴
正方向
y轴或纵轴
正方向
平面直角坐标系的原点
课后练习
B
(+,+)
(-,+)
(-,-)
(+,-)
(0,0)
|b|
|a|
D
A
【答案】B
C
D
D
【答案】C
再见
第七章
7.1.2
平面直角坐标系
人教版数学七年级下册
1.认识平面直角坐标系,了解点的坐标的意义.
2.会用坐标表示点,能画出点的坐标位.
学习目标
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2.反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了.
A
B
如何确定直线上点的位置?
1米
导入新知
1
知识点
平面直角坐标系
如何确定平面上点的位置呢?
合作探究
平面直角坐标系:平面上互相垂直且有公共原点的
两条数轴构成平面直角坐标系,
简称为直角坐标系.
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
坐标原点
注意:
坐标轴上的点不属于任何象限.
相关概念:
水平的数轴叫做x轴或横轴,习惯上取向右为正方
向;铅直的数轴叫做y轴或纵轴,取向上为正方向;
x轴和y轴统称坐标轴,它们的公共原点O称为平面
直角坐标系的原点.
下列语句不正确的是( )
A.平面直角坐标系中,两条互相垂直的数轴的交点是原点
B.平面直角坐标系所在的平面叫坐标平面
C.平面直角坐标系中x轴、y轴把坐标平面分成4部分
D.凡是两条互相垂直的直线都能组成平面直角坐标系
例1
D
导引:
本题主要考查平面直角坐标系的概念.根据平
面直角坐标系的概念可知A,B,C项正确.D
项不正确,因为平面直角坐标系必须由数轴构
成,且构成平面直角坐标系的两条数轴互相垂
直、原点重合.
本题应用定义法,要正确理解平面直角坐标系的
概念.
理解并认识平面直角坐标系必须明确:(1)建立平
面直角坐标系的平面叫坐标平面;(2)平面直角坐标系
必须具备:①由两条数轴组成;②这两条数轴有公共
原点且互相垂直.
新知小结
1
下列说法错误的是( )
A.平面内两条互相垂直的数轴就构成了平面直
角坐标系
B.平面直角坐标系中两条数轴是互相垂直的
C.坐标平面被两条坐标轴分成了四个部分,每
个部分称为象限
D.坐标轴上的点不属于任何象限
A
巩固新知
2
知识点
平面直角坐标系内点的坐标
1、直角坐标系的横轴和纵轴将平面分成
____
部分,
从右上方的部分说起,按逆时针方向,各部分
依次是__________、
_________
、
_________
和__________.
2、坐标轴上的点属于哪一象限?
四
第一象限
第二象限
第三象限
第四象限
合作探究
-5
5
5
1
2
3
4
1
2
3
4
-2
-3
-4
x
-4
-3
-2
-1
-1
O
y
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
原点的坐标为(0,0)
各象限的坐标符号特征:
1、点P(x,y)在第一象限
x>0,y>0.
2、点P(x,y)在第二象限
x<0,y>0.
3、点P(x,y)在第三象限
x<0,y<0.
4、点P(x,y)在第四象限
x>0,y<0.
例在平面直角坐标系(如图)中描出下列各点:
A(4,5),
B(-2,3),
C(-4,-1),
D(2.5,-2),
E(0,-4).
例2
解:
如图,先在x轴上找出表示4的点,再在y轴上找出
表示5的点,过这两个点分别作x轴和y轴的垂线,
垂线的交点就是点A.
类似地,请你在图上
描出点B,C,D,E.
由点的坐标确定点的位置的方法:方法一是由点
的坐标的符号确定点的位置,即(+,+)的点在第一
象限,(-,+)的点在第二象限,(-,-)的点在第三
象限,(+,-)的点在第四象限;方法二是分别过两
坐标轴上表示该点的坐标的点作两坐标轴的垂线,这
两条垂线的交点位置即为该点的位置.
新知小结
1
写出图中点A,B,C,D,E,F的坐标.
解:
A点的坐标为(-2,-2),
B点的坐标为(-5,4),
C点的坐标为(5,-4),D点的坐标为(0,-3),
E点的坐标为(2,5),F点的坐标为(-3,0).
巩固新知
2
下列说法错误的是( )
A.象限内的点的坐标可用一个有序数对来表示
B.坐标轴上的点的坐标可用一个有序数对来表
示
C.过点P向x轴作垂线,点P与垂足之间的线段
长是点P的纵坐标
D.过点P向y轴作垂线,点P与垂足之间的线段
长不一定是点P的横坐标
C
3
【中考·荆门】在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
4
在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
A.(-3,300)
B.(7,-500)
C.(9,600)
D.(-2,-800)
C
3
知识点
点的位置与点的坐标的关系
点M(x,y)所处的位置
坐标特征
在x轴正半轴上:M(正,0)
在x轴负半轴上:M(负,0)
在y轴正半轴上:M(0,正)
在y轴负半轴上:M(0,负)
坐标轴上的点的坐标:
点M在x轴上
点M在y轴上
合作探究
拓展:
平行于x轴的直线上的点的纵坐标相等;
平行于y轴的直线上的点的横坐标相等.
例3
已知点P(x+6,x-4)在y轴上,则点P
的坐标是__________.
导引:根据y轴上点的坐标的特征可得x+6=
0,得x=-6,所以x-4=-10.故点P
的坐标是(0,-10).
(0,-10)
1
【中考·台湾】如图为A,B,C三点在坐标平面上的位置图.若A,B,C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
A.5
B.3
C.-3
D.-5
B
巩固新知
平面直角坐标系的三要素:
(1)两条数轴;
(2)互相告直;
(3)公共原点.
1
知识小结
归纳新知
2.
第一、二、三、四象限内点的坐标的符号依次
为(+,+),(-,+),(-,-),(+,-).
3.x轴上的点纵坐标为0,y轴上的点横坐标为0.
4.
建立坐标系常用的方法有:
(1)以图形上的某已知点或线段的中点为原点;
(2)以图形上某线段所在直线为x
轴(或y
轴);
(3)利用图形的轴对称性以对称轴为x
轴(或y
轴).
若点P(a,b)在第二象限,则点M(b-a,a-b)
在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
2
易错小结
易错点:对直角坐标系内的点的坐标的符号理解不清
而致错.
A或B或C
错解:
错解产生的原因有两个:一是对各象限内点的坐标特点没有掌握好,二是没有弄清b-a与a-b的符号.
诊断:
根据各象限内的点的坐标的符号特点,先判定a与b的符号,再确定b-a与a-b的符号.
解题策略:
原点重合
平面直角坐标系
x轴或横轴
正方向
y轴或纵轴
正方向
平面直角坐标系的原点
课后练习
B
(+,+)
(-,+)
(-,-)
(+,-)
(0,0)
|b|
|a|
D
A
【答案】B
C
D
D
【答案】C
再见
