6.2.1立方根的概念课件(22张)
图片预览







文档简介
(共22张PPT)
一个正数有两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.
活动一:温故导新
如果
=a
,那么x叫做a的平方根.
X2
定义一:
性质:
1.回顾:
平方根是怎样定义的?平方根有哪些性质?
2.当a≥0时,式子
的意义是什么?
a
要制作一种体积为27m?
的包装箱,这种包装箱的边长应该是多少?
这就是求一个数x,
所以x=(
).
的正方体形状
设这种包装箱的边长为x
m,则:
使它的立方等于27,
3
3
因为
3
探讨问题:
即这种包装箱的边长应为
m
6.2
立方根
—人人学有价值的数学;
—人人都能获得必需的数学;
—不同的人在数学上得到不同发展;
人民教育出版社义务教育教科书七年级下册
【学习目标】
1、知道立方根的概念,初步学会用
根号表示一个数的立方根.
2、知道立方与开立方互为逆运算,
会用立方运算求某些数的立方根.
3、体会一个数的立方根的惟一性,
分清一个数的立方根与平方根的区别.
【学习重点】立方根的概念和求法.
【学习难点】立方根与平方根的区别.
活动二:探索新知
1、我们知道:若(
)2
=
49,(
)2
=
9
如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.
求一个数的立方根的运算,叫做开立方.
试一试:你能给数的立方根下个定义吗?
±7
3
(
)3
=
-
64
±3
-
4
那么,49的平方根是
;9的平方根是
.
也就是:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.
做一做:
即:如果
x3
=
a,那么x叫做a的立方根.
.
2、探一探:根据立方根的意义填空:
1)∵(
)3
=8,∴8的立方根是( );
2)∵(
)3=0.125,∴0.125的立方根是(
);
3)∵(
)3=0,∴0的立方根是( );
4)∵(
)3
=-8,∴-8的立方根是(
);
5)∵(
)3
=
,∴
的立方根是(
)
2
2
0.5
0.5
0
0
-2
-2
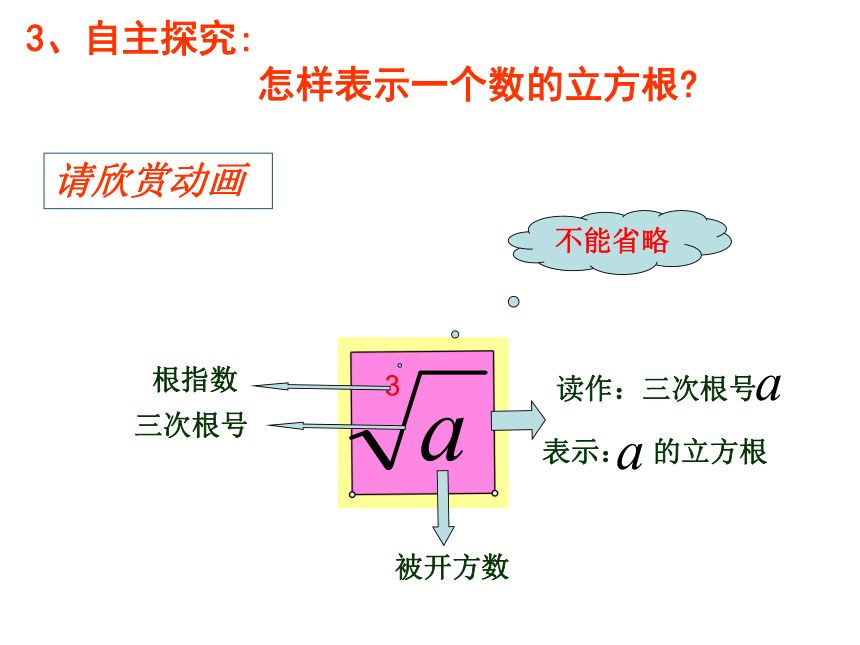
3
三次根号
根指数
被开方数
表示:
的立方根
不能省略
读作:三次根号
请欣赏动画
3、自主探究:
怎样表示一个数的立方根?
一个数
的立方根,用符号“
”表示,
读作:“三次根号
”,其中
叫做
被开方数
3叫
,不能省略,若省略表示平方.
根指数
例如:8的立方根是
2;
-8的立方根是
-2;
可以表示为:
3
=2
3
=
-2
语言叙述
你会读吗?它们表示的意义是什么?
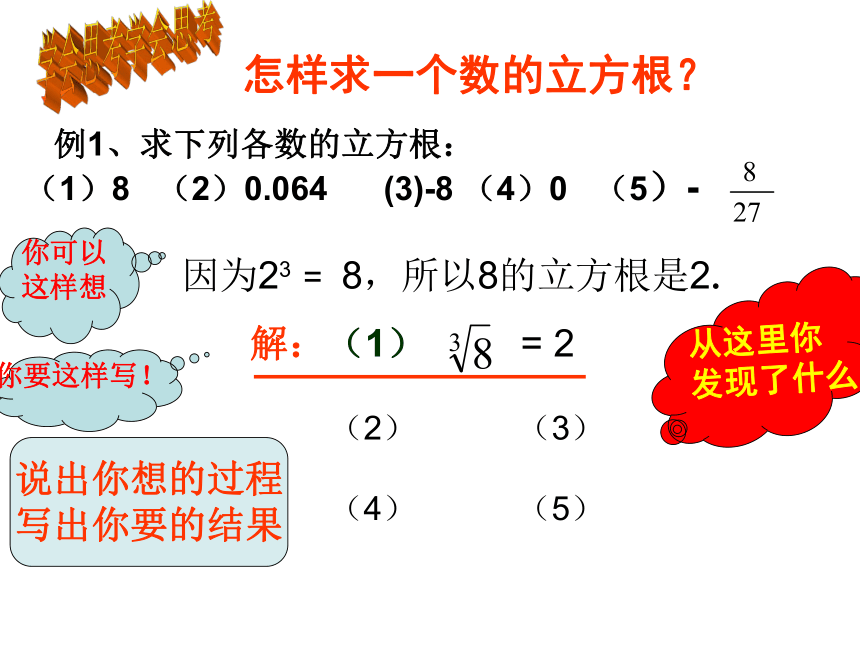
怎样求一个数的立方根?
学会思考
例1、求下列各数的立方根:
(1)8
(2)0.064
(3)-8
(4)0
(5)-
你可以
这样想
因为23
=
8,所以8的立方根是2.
你要这样写!
说出你想的过程
写出你要的结果
(2)
(3)
(4)
(5)
解:(1)
=
2
从这里你
发现了什么?
活动三:归纳发现
正数的立方根是____________,
负数的立方根______________,
0的立方根______________,
任何数都有_________立方根.
正数
负数
0
唯一一个
平方根
立方根
正数
负数
0
讨论:
你能指出平方根和立方根
的异同点吗?
有两个,互为相反数
没有平方根
0
有一个,是正数
有一个,是负数
0
解:
(3)
(4)
=
4
(3)
(2)
=
(1)
=
0.5
(4)
=
=
例2、下列式子中,你能求出它们的值吗?
当堂检测:
判断下列说法是否正确,并说明理由
x
(3)
任何数的立方根都只有一个
(
)
(5)
如果一个数的立方根是这个数的本身,那么这个数一定
是零;
(
)
x
x
(7)
-64没有立方根。
(
)
x
(1)
25的立方根是5
(
)
(6)
一个数的立方根不是正数就是负数
√
(
)
(2)
互为相反数的两个数,它们的立方根也互为相反数;
(
)
√
(4)如果一个数的平方根与其立方根相同,则
这个数是1;
(
)
x
2.(1)-512的立方根是_______;
的立方根是_______
;
的立方根是_______。
(2)
是
的平方根,
是
的立方根。
(3)
的立方根是________.
是_______的立方根.
(4)
通过这节课的学习,同学们有什么收获?
(1)立方根定义,性质,及表示方法.
(2)求一个数的立方根.
(3)立方根和平方根的区别.
课堂小结:
作业布置
1、订正本张讲学稿(有能力的同学把拓展延伸做完);
2、做下一张讲学稿预习部分。
2017年3月23日
再
见
自我检测:
1、16的平方根是
2、一个数的平方根与它的立方根相等,
则这个数是
3、(2009,中考)
8的立方根是(
).
A、2
B、±2
C、4
D、
±4
——.
——.
±4
0
A
4、(2009,中考)
的绝对值是(
)
A、-3
B、3
C、
D、
-
B
A卷
B卷
1、-1的立方根是___
.
2、1的平方根是____;1立方根是_____.
3、0.064的立方根是_____.
-1
±1
1
=
____.
0.4
-0.3
4、0的平方根是_____,0的立方根是____.
0
0
1、结论:
(1)求一个数的立方根的运算叫做开立方.
开立方与立方互为逆运算.
(2)利用开立方和立方互为逆运算关系,求一个数的立方根,就可以利用这种互逆关系,检验其正确性.
活动四:
巩固小结
立方
开立方
互
逆
求下列各数的值
(1)
(2)
(3)
(4)
解:
(1)
=
2
(2)
=
-0.2
(3)
=
=
(4)
=
=
-1
-----------反馈练习-----------
活动五:应用新知
习题6.2
1、P51
第1题;
2、P52
第3题
.
一个正数有两个平方根,它们互为相反数;零的平方根是零,负数没有平方根.
活动一:温故导新
如果
=a
,那么x叫做a的平方根.
X2
定义一:
性质:
1.回顾:
平方根是怎样定义的?平方根有哪些性质?
2.当a≥0时,式子
的意义是什么?
a
要制作一种体积为27m?
的包装箱,这种包装箱的边长应该是多少?
这就是求一个数x,
所以x=(
).
的正方体形状
设这种包装箱的边长为x
m,则:
使它的立方等于27,
3
3
因为
3
探讨问题:
即这种包装箱的边长应为
m
6.2
立方根
—人人学有价值的数学;
—人人都能获得必需的数学;
—不同的人在数学上得到不同发展;
人民教育出版社义务教育教科书七年级下册
【学习目标】
1、知道立方根的概念,初步学会用
根号表示一个数的立方根.
2、知道立方与开立方互为逆运算,
会用立方运算求某些数的立方根.
3、体会一个数的立方根的惟一性,
分清一个数的立方根与平方根的区别.
【学习重点】立方根的概念和求法.
【学习难点】立方根与平方根的区别.
活动二:探索新知
1、我们知道:若(
)2
=
49,(
)2
=
9
如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.
求一个数的立方根的运算,叫做开立方.
试一试:你能给数的立方根下个定义吗?
±7
3
(
)3
=
-
64
±3
-
4
那么,49的平方根是
;9的平方根是
.
也就是:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根.
做一做:
即:如果
x3
=
a,那么x叫做a的立方根.
.
2、探一探:根据立方根的意义填空:
1)∵(
)3
=8,∴8的立方根是( );
2)∵(
)3=0.125,∴0.125的立方根是(
);
3)∵(
)3=0,∴0的立方根是( );
4)∵(
)3
=-8,∴-8的立方根是(
);
5)∵(
)3
=
,∴
的立方根是(
)
2
2
0.5
0.5
0
0
-2
-2
3
三次根号
根指数
被开方数
表示:
的立方根
不能省略
读作:三次根号
请欣赏动画
3、自主探究:
怎样表示一个数的立方根?
一个数
的立方根,用符号“
”表示,
读作:“三次根号
”,其中
叫做
被开方数
3叫
,不能省略,若省略表示平方.
根指数
例如:8的立方根是
2;
-8的立方根是
-2;
可以表示为:
3
=2
3
=
-2
语言叙述
你会读吗?它们表示的意义是什么?
怎样求一个数的立方根?
学会思考
例1、求下列各数的立方根:
(1)8
(2)0.064
(3)-8
(4)0
(5)-
你可以
这样想
因为23
=
8,所以8的立方根是2.
你要这样写!
说出你想的过程
写出你要的结果
(2)
(3)
(4)
(5)
解:(1)
=
2
从这里你
发现了什么?
活动三:归纳发现
正数的立方根是____________,
负数的立方根______________,
0的立方根______________,
任何数都有_________立方根.
正数
负数
0
唯一一个
平方根
立方根
正数
负数
0
讨论:
你能指出平方根和立方根
的异同点吗?
有两个,互为相反数
没有平方根
0
有一个,是正数
有一个,是负数
0
解:
(3)
(4)
=
4
(3)
(2)
=
(1)
=
0.5
(4)
=
=
例2、下列式子中,你能求出它们的值吗?
当堂检测:
判断下列说法是否正确,并说明理由
x
(3)
任何数的立方根都只有一个
(
)
(5)
如果一个数的立方根是这个数的本身,那么这个数一定
是零;
(
)
x
x
(7)
-64没有立方根。
(
)
x
(1)
25的立方根是5
(
)
(6)
一个数的立方根不是正数就是负数
√
(
)
(2)
互为相反数的两个数,它们的立方根也互为相反数;
(
)
√
(4)如果一个数的平方根与其立方根相同,则
这个数是1;
(
)
x
2.(1)-512的立方根是_______;
的立方根是_______
;
的立方根是_______。
(2)
是
的平方根,
是
的立方根。
(3)
的立方根是________.
是_______的立方根.
(4)
通过这节课的学习,同学们有什么收获?
(1)立方根定义,性质,及表示方法.
(2)求一个数的立方根.
(3)立方根和平方根的区别.
课堂小结:
作业布置
1、订正本张讲学稿(有能力的同学把拓展延伸做完);
2、做下一张讲学稿预习部分。
2017年3月23日
再
见
自我检测:
1、16的平方根是
2、一个数的平方根与它的立方根相等,
则这个数是
3、(2009,中考)
8的立方根是(
).
A、2
B、±2
C、4
D、
±4
——.
——.
±4
0
A
4、(2009,中考)
的绝对值是(
)
A、-3
B、3
C、
D、
-
B
A卷
B卷
1、-1的立方根是___
.
2、1的平方根是____;1立方根是_____.
3、0.064的立方根是_____.
-1
±1
1
=
____.
0.4
-0.3
4、0的平方根是_____,0的立方根是____.
0
0
1、结论:
(1)求一个数的立方根的运算叫做开立方.
开立方与立方互为逆运算.
(2)利用开立方和立方互为逆运算关系,求一个数的立方根,就可以利用这种互逆关系,检验其正确性.
活动四:
巩固小结
立方
开立方
互
逆
求下列各数的值
(1)
(2)
(3)
(4)
解:
(1)
=
2
(2)
=
-0.2
(3)
=
=
(4)
=
=
-1
-----------反馈练习-----------
活动五:应用新知
习题6.2
1、P51
第1题;
2、P52
第3题
.
