2020-2021学年人教版八年级下册数学 18.1平行四边形 同步习题 (Word版 含解析)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 18.1平行四边形 同步习题 (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 148.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 19:09:58 | ||
图片预览




文档简介
18.1平行四边形 同步习题
一.选择题
1.平行四边形中较大的内角的度数是较小的内角的度数的4倍,则其中较小的内角的度数是( )
A.30° B.36° C.45° D.60°
2.有长度分别为6cm,8cm,10cm的铁丝三根,取其中一根作为边,另外两根作为对角线.下列取法中,能搭成一个平行四边形的是( )
A.取10cm长的铁丝为边
B.取8cm长的铁丝为边
C.取6cm长的铁丝为边
D.任意取一根铁丝为边均可
3.?ABCD的四个内角的度数之比∠A:∠B:∠C:∠D可能是( )
A.2:5:2:5 B.3:4:4:3 C.4:4:2:2 D.2:3:4:5
4.下列各组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AB=CD
C.∠A:∠B:∠C:∠D=5:5:6:6 D.OA=OC,OB=OD
5.如图,?ABCD的两条对角线交于点O,AC=4,BD=5,BC=3,则△BOC的周长为( )
A.7.5 B.12 C.6 D.无法确定
6.如图,在△MBN中,BM=8,BN=6,点A,C,D分别是MB,NB,MN的中点,则平行四边形ABCD的周长是( )
A.16 B.18 C.14 D.32
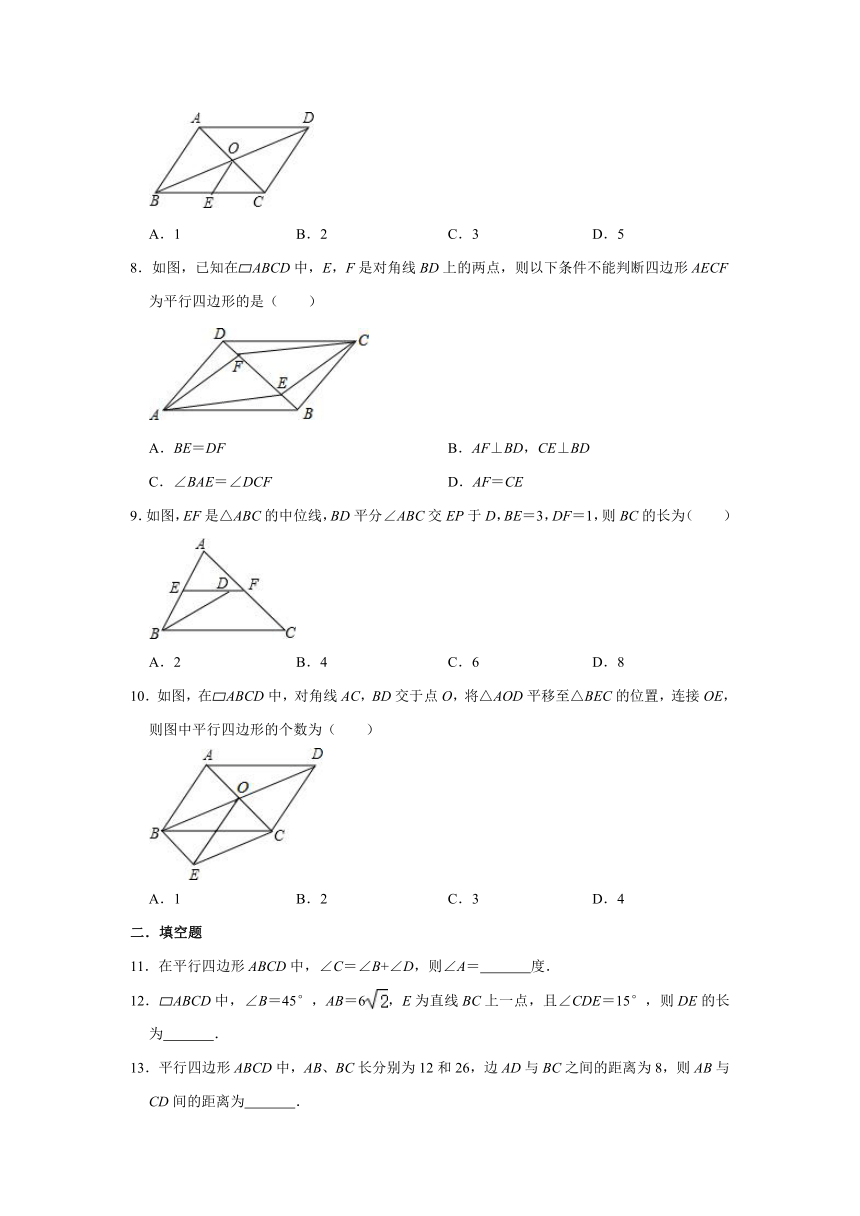
7.如图,在平行四边形ABCD中,AC与BD交于点O,E是BC边的中点,AB=4,则OE的长为( )
A.1 B.2 C.3 D.5
8.如图,已知在?ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )
A.BE=DF B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF D.AF=CE
9.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2 B.4 C.6 D.8
10.如图,在?ABCD中,对角线AC,BD交于点O,将△AOD平移至△BEC的位置,连接OE,则图中平行四边形的个数为( )
A.1 B.2 C.3 D.4
二.填空题
11.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 度.
12.?ABCD中,∠B=45°,AB=6,E为直线BC上一点,且∠CDE=15°,则DE的长为 .
13.平行四边形ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为 .
14.如图,?ABCD中,EF过对角线的交点O如果AB=4cm,AD=3cm,OF=1cm,则四边形BCEF的周长为 .
15.如图,平行四边形ABCD中,AB=8,AD=10,以CD为边向内作等边△CDE,连接AE,F为AE中点,连接BF,过E作EG∥BF交BC于G,则当BF⊥AE时,EG为 .
三.解答题
16.如图,在平行四边形ABCD中,点E,F为对角线AC上的两点,且AE=CF,连接DE,BF.
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
17.如图,在?ABCD中,O是BD的中点,E、F分别是BC、AD的中点,M、N分别是OB、OD中点.求证:四边形MENF是平行四边形.
18.如图,在四边形ABCD中,AB=CD,点E在DC的延长线上,连接BE交AD于点F,BE平分∠ABC,BC=EC,作FG⊥BA延长线于点G.
(1)求证:四边形ABCD为平行四边形;
(2)若F为AD中点,EF=6,BC=2,求GF的长.
参考答案
一.选择题
1.解:如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=4∠B,
∴∠B+4∠B=180°,
解得:∠B=36°,
故选:B.
2.解:A、取10cm长的铁丝为边时,
∵×6=3,×8=4,3+4<10,不能构成三角形,
则不能构成平行四边形,选项A不符合题意;
B、取8cm长的铁丝为边时,
∵×6=3,×10=5,3+5=8,不能构成三角形,
则不能构成平行四边形,选项B不符合题意;
C、取6cm长的铁丝为边时,
∵×8=4,×10=5,4+5>6,能构成三角形,
则能构成平行四边形,选项C符合题意;
D、任意取一根铁丝为边时,不一定能构成三角形,
则不一定能构成平行四边形,选项D不符合题意;
故选:C.
3.解:在平行四边形中,两组对角相等,即∠A=∠C,∠B=∠D,
所以在A、B、C、D四个选项中,只有A选项符合要求.
故选:A.
4.解:A、“AB=CD,AD=BC”是四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
B、“AB∥CD,AB=CD”是四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
C、“∠A:∠B:∠C:∠D=5:5:6:6”是四边形ABCD的两组邻角相等,该四边形可以是等腰梯形;故本选项符合题意.
D、“OA=OC,OB=OD”是四边形ABCD的对角线互相平分,则四边形ABCD是平行四边形;故本选项不符合题意;
故选:C.
5.解:∵?ABCD的两条对角线交于点0,AC=4,BD=5,BC=3,
∴BO=DO=2.5,AO=CO=2,
∴△BOC的周长为:BO+CO+BC=2.5+2+3=7.5.
故选:A.
6.解:如图,∵BM=8,BN=6,点A,C,D分别是MB,NB,MN的中点,
∴AD、CD是△BMN的中位线,
∴AD=BN=3,CD=MB=4,
∴平行四边形ABCD的周长是2(AD+CD)=14.
故选:C.
7.解:在平行四边形ABCD中,AO=CO,
∵点E是BC的中点,
∴OE是△ABC的中位线,
∴OE=AB=2cm.
故选:B.
8.解:如图,连接AC与BD相交于O,
在?ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项错误;
B、若AF⊥BD,CE⊥BD,则可以利用“角角边”证明△ADF和△CBE全等,从而得到DF=BE,然后同A,故本选项错误;
C、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项错误;
D、AF=CE无法证明得到OE=OF,故本选项正确.
故选:D.
9.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵EF是△ABC的中位线,
∴EF∥BC,BC=2EF,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴ED=EB=3,
∴EF=ED+DF=4,
∴BC=2EF=8,
故选:D.
10.解:图中平行四边形的个数为4个,分别为平行四边形ABCD,平行四边形BEOC,平行四边形ABEO,平行四边形OECD,
由△AOD平移至△BEC的位置,得到BE∥AO,且BE=AO,即四边形ABEO为平行四边形;
得到OD∥EC,且OD=EC,即四边形OECD为平行四边形;
∵四边形ABCD为平行四边形,
∴OA=OC,OD=OB,
∵OA=BE,OD=EC,
∴OC=BE,OB=CE,
∴四边形OBEC为平行四边形.
故选:D.
二.填空题
11.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,∠A=∠C,
∴∠C=∠B+∠D=2∠D,∠C+∠D=180°,
∴∠A=∠C=120°,
故答案为:120.
12.解:如图1,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ADC=∠B=45°,
过A作AH⊥BC于H,过EF⊥AD于F,
则四边形AHEF是矩形,∠AHB=∠DFE=90°,
∴AH=EF,
∵∠B=45°,AB=6,
∴AH=EF=AB=6,
∵∠CDE=15°,
∴∠EDF=30°,
∴DE=2EF=12;
如图2,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ADC=∠B=45°,
过A作AH⊥BC于H,过EF⊥AD于F,
则四边形AHEF是矩形,∠AHB=∠DFE=90°,
∴AH=EF,
∵∠B=45°,AB=6,
∴AH=EF=AB=6,
∵∠CDE=15°,
∴∠EDF=60°,
∴∠FED=30°,
∵EF=6,
∴DE=EF=4;
综上所述,DE的长为12或4.
故答案为:12或4.
13.解:如图,过点A作AE⊥BC于点E、AF⊥CD于点F.
由题意得,S四边形ABCD=AE×BC=CD×AF,
∵AB=12,BC=26,AE=8,
∴26×8=12×AF,
∴AF=,
即AB与CD间的距离为.
故答案是:.
14.解:根据平行四边形的性质,得
DO=OB,∠FDO=∠EBO,又∠DOF=∠BOE,
∴△ODF≌△OBE,
∴OF=OE=1,DF=BE,
根据平行四边形的对边相等,得
CD=AB=4,AD=BC=3,
故四边形EFBC的周长=EF+EB+FC+BC
=OE+OF+DF+FC+BC
=1+1+4+3=9.
故答案为9cm.
15.解:在GC上取点M,使得CM=BG,连接EM.
∵F是AE的中点,BF⊥AE,
∴AB=BE,
∵BF⊥AE,
∴∠3=∠4,
∵四边形ABCD是平行四边形,
∴AB=CD=8,BC=AD=10,AB∥CD,
∵△CDE是等边三角形,
∴CE=CD=AB=8,∠ECD=60°,
∵AB=BE,AB=CD,
∴BE=CE,
∴∠1=∠2,
∵CG=BG,
∴△EBG≌△ECM(SAS),
∴EG=EM,
∵AB∥CD,
∴∠ABC+∠DCB=180°,即∠ECD+∠1+∠2+∠3+∠4=180°,
∵∠1=∠2,∠3=∠4,∠ECD=60°,
∴∠2+∠3=60°,即∠FBC=60°,
∵EG∥BF,
∴∠EGC=∠FBC=60°,
∵GE=EM,
∴△EMG是等边三角形,
∴CG=CM+MG=BG+GE,
过E作EH⊥BC于H,
则BH=CH=BC=AD=5,
∴EH===,
∴EG=2,
故答案为:2.
三.解答题
16.(1)解:△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;
理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=CB,AB∥CD,AD∥CB,
∴∠BAF=∠DCE,∠DAE=∠BCF,
在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS);
∵AE=CF,
∴AF=CE,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS);
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)证明:∵△ABF≌△△CDE,
∴∠AFB=∠CED,
∴DE∥BF.
17.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠FDN=∠EBM,
∵E、F分别是BC、AD的中点,
∴DF=BE,
∵O是BD的中点,
∴OD=OB,
∵M、N分别是OB、OD中点,
∴DN=BM,
在△DNF和△BME中,,
∴△DNF≌△BME(SAS),
∴FN=EM,∠DNF=∠BME,
∴∠FNM=∠EMN,
∴FN∥EM,
∴四边形MENF是平行四边形.
18.(1)证明:∵BE平分∠ABC,BC=EC,
∴∠ABF=∠CBE,∠CBE=∠E,
∴∠ABF=∠E,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD为平行四边形;
(2)解:由(1)得:四边形ABCD为平行四边形,
∴AD=BC=2,
∵F为AD中点,
∴AF=DF=,
在△ABF和△DEF中,,
∴△ABF≌△DEF(AAS),
∴BF=EF=6,AB=DE,
∵AB=CD,
∴AB=CD=DE=CE=BC=,
∵FG⊥AB,
∴∠G=90°,
∴GF2=AF2﹣AG2=BF2﹣BG2,
即()2﹣AG2=62﹣(+AG)2,
解得:AG=,
∴GF==.
一.选择题
1.平行四边形中较大的内角的度数是较小的内角的度数的4倍,则其中较小的内角的度数是( )
A.30° B.36° C.45° D.60°
2.有长度分别为6cm,8cm,10cm的铁丝三根,取其中一根作为边,另外两根作为对角线.下列取法中,能搭成一个平行四边形的是( )
A.取10cm长的铁丝为边
B.取8cm长的铁丝为边
C.取6cm长的铁丝为边
D.任意取一根铁丝为边均可
3.?ABCD的四个内角的度数之比∠A:∠B:∠C:∠D可能是( )
A.2:5:2:5 B.3:4:4:3 C.4:4:2:2 D.2:3:4:5
4.下列各组条件中,不能判定四边形ABCD是平行四边形的是( )
A.AB=CD,AD=BC B.AB∥CD,AB=CD
C.∠A:∠B:∠C:∠D=5:5:6:6 D.OA=OC,OB=OD
5.如图,?ABCD的两条对角线交于点O,AC=4,BD=5,BC=3,则△BOC的周长为( )
A.7.5 B.12 C.6 D.无法确定
6.如图,在△MBN中,BM=8,BN=6,点A,C,D分别是MB,NB,MN的中点,则平行四边形ABCD的周长是( )
A.16 B.18 C.14 D.32
7.如图,在平行四边形ABCD中,AC与BD交于点O,E是BC边的中点,AB=4,则OE的长为( )
A.1 B.2 C.3 D.5
8.如图,已知在?ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )
A.BE=DF B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF D.AF=CE
9.如图,EF是△ABC的中位线,BD平分∠ABC交EP于D,BE=3,DF=1,则BC的长为( )
A.2 B.4 C.6 D.8
10.如图,在?ABCD中,对角线AC,BD交于点O,将△AOD平移至△BEC的位置,连接OE,则图中平行四边形的个数为( )
A.1 B.2 C.3 D.4
二.填空题
11.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 度.
12.?ABCD中,∠B=45°,AB=6,E为直线BC上一点,且∠CDE=15°,则DE的长为 .
13.平行四边形ABCD中,AB、BC长分别为12和26,边AD与BC之间的距离为8,则AB与CD间的距离为 .
14.如图,?ABCD中,EF过对角线的交点O如果AB=4cm,AD=3cm,OF=1cm,则四边形BCEF的周长为 .
15.如图,平行四边形ABCD中,AB=8,AD=10,以CD为边向内作等边△CDE,连接AE,F为AE中点,连接BF,过E作EG∥BF交BC于G,则当BF⊥AE时,EG为 .
三.解答题
16.如图,在平行四边形ABCD中,点E,F为对角线AC上的两点,且AE=CF,连接DE,BF.
(1)写出图中所有的全等三角形;
(2)求证:DE∥BF.
17.如图,在?ABCD中,O是BD的中点,E、F分别是BC、AD的中点,M、N分别是OB、OD中点.求证:四边形MENF是平行四边形.
18.如图,在四边形ABCD中,AB=CD,点E在DC的延长线上,连接BE交AD于点F,BE平分∠ABC,BC=EC,作FG⊥BA延长线于点G.
(1)求证:四边形ABCD为平行四边形;
(2)若F为AD中点,EF=6,BC=2,求GF的长.
参考答案
一.选择题
1.解:如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=4∠B,
∴∠B+4∠B=180°,
解得:∠B=36°,
故选:B.
2.解:A、取10cm长的铁丝为边时,
∵×6=3,×8=4,3+4<10,不能构成三角形,
则不能构成平行四边形,选项A不符合题意;
B、取8cm长的铁丝为边时,
∵×6=3,×10=5,3+5=8,不能构成三角形,
则不能构成平行四边形,选项B不符合题意;
C、取6cm长的铁丝为边时,
∵×8=4,×10=5,4+5>6,能构成三角形,
则能构成平行四边形,选项C符合题意;
D、任意取一根铁丝为边时,不一定能构成三角形,
则不一定能构成平行四边形,选项D不符合题意;
故选:C.
3.解:在平行四边形中,两组对角相等,即∠A=∠C,∠B=∠D,
所以在A、B、C、D四个选项中,只有A选项符合要求.
故选:A.
4.解:A、“AB=CD,AD=BC”是四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
B、“AB∥CD,AB=CD”是四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
C、“∠A:∠B:∠C:∠D=5:5:6:6”是四边形ABCD的两组邻角相等,该四边形可以是等腰梯形;故本选项符合题意.
D、“OA=OC,OB=OD”是四边形ABCD的对角线互相平分,则四边形ABCD是平行四边形;故本选项不符合题意;
故选:C.
5.解:∵?ABCD的两条对角线交于点0,AC=4,BD=5,BC=3,
∴BO=DO=2.5,AO=CO=2,
∴△BOC的周长为:BO+CO+BC=2.5+2+3=7.5.
故选:A.
6.解:如图,∵BM=8,BN=6,点A,C,D分别是MB,NB,MN的中点,
∴AD、CD是△BMN的中位线,
∴AD=BN=3,CD=MB=4,
∴平行四边形ABCD的周长是2(AD+CD)=14.
故选:C.
7.解:在平行四边形ABCD中,AO=CO,
∵点E是BC的中点,
∴OE是△ABC的中位线,
∴OE=AB=2cm.
故选:B.
8.解:如图,连接AC与BD相交于O,
在?ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项错误;
B、若AF⊥BD,CE⊥BD,则可以利用“角角边”证明△ADF和△CBE全等,从而得到DF=BE,然后同A,故本选项错误;
C、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项错误;
D、AF=CE无法证明得到OE=OF,故本选项正确.
故选:D.
9.解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵EF是△ABC的中位线,
∴EF∥BC,BC=2EF,
∴∠EDB=∠CBD,
∴∠ABD=∠EDB,
∴ED=EB=3,
∴EF=ED+DF=4,
∴BC=2EF=8,
故选:D.
10.解:图中平行四边形的个数为4个,分别为平行四边形ABCD,平行四边形BEOC,平行四边形ABEO,平行四边形OECD,
由△AOD平移至△BEC的位置,得到BE∥AO,且BE=AO,即四边形ABEO为平行四边形;
得到OD∥EC,且OD=EC,即四边形OECD为平行四边形;
∵四边形ABCD为平行四边形,
∴OA=OC,OD=OB,
∵OA=BE,OD=EC,
∴OC=BE,OB=CE,
∴四边形OBEC为平行四边形.
故选:D.
二.填空题
11.解:∵四边形ABCD是平行四边形,
∴AD∥BC,∠B=∠D,∠A=∠C,
∴∠C=∠B+∠D=2∠D,∠C+∠D=180°,
∴∠A=∠C=120°,
故答案为:120.
12.解:如图1,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ADC=∠B=45°,
过A作AH⊥BC于H,过EF⊥AD于F,
则四边形AHEF是矩形,∠AHB=∠DFE=90°,
∴AH=EF,
∵∠B=45°,AB=6,
∴AH=EF=AB=6,
∵∠CDE=15°,
∴∠EDF=30°,
∴DE=2EF=12;
如图2,
∵四边形ABCD是平行四边形,
∴AD∥BC,∠ADC=∠B=45°,
过A作AH⊥BC于H,过EF⊥AD于F,
则四边形AHEF是矩形,∠AHB=∠DFE=90°,
∴AH=EF,
∵∠B=45°,AB=6,
∴AH=EF=AB=6,
∵∠CDE=15°,
∴∠EDF=60°,
∴∠FED=30°,
∵EF=6,
∴DE=EF=4;
综上所述,DE的长为12或4.
故答案为:12或4.
13.解:如图,过点A作AE⊥BC于点E、AF⊥CD于点F.
由题意得,S四边形ABCD=AE×BC=CD×AF,
∵AB=12,BC=26,AE=8,
∴26×8=12×AF,
∴AF=,
即AB与CD间的距离为.
故答案是:.
14.解:根据平行四边形的性质,得
DO=OB,∠FDO=∠EBO,又∠DOF=∠BOE,
∴△ODF≌△OBE,
∴OF=OE=1,DF=BE,
根据平行四边形的对边相等,得
CD=AB=4,AD=BC=3,
故四边形EFBC的周长=EF+EB+FC+BC
=OE+OF+DF+FC+BC
=1+1+4+3=9.
故答案为9cm.
15.解:在GC上取点M,使得CM=BG,连接EM.
∵F是AE的中点,BF⊥AE,
∴AB=BE,
∵BF⊥AE,
∴∠3=∠4,
∵四边形ABCD是平行四边形,
∴AB=CD=8,BC=AD=10,AB∥CD,
∵△CDE是等边三角形,
∴CE=CD=AB=8,∠ECD=60°,
∵AB=BE,AB=CD,
∴BE=CE,
∴∠1=∠2,
∵CG=BG,
∴△EBG≌△ECM(SAS),
∴EG=EM,
∵AB∥CD,
∴∠ABC+∠DCB=180°,即∠ECD+∠1+∠2+∠3+∠4=180°,
∵∠1=∠2,∠3=∠4,∠ECD=60°,
∴∠2+∠3=60°,即∠FBC=60°,
∵EG∥BF,
∴∠EGC=∠FBC=60°,
∵GE=EM,
∴△EMG是等边三角形,
∴CG=CM+MG=BG+GE,
过E作EH⊥BC于H,
则BH=CH=BC=AD=5,
∴EH===,
∴EG=2,
故答案为:2.
三.解答题
16.(1)解:△ABC≌△CDA,△ABF≌△△CDE,△ADE≌△CBF;
理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,AD=CB,AB∥CD,AD∥CB,
∴∠BAF=∠DCE,∠DAE=∠BCF,
在△ABC和△CDA中,
,
∴△ABC≌△CDA(SSS);
∵AE=CF,
∴AF=CE,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(SAS);
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)证明:∵△ABF≌△△CDE,
∴∠AFB=∠CED,
∴DE∥BF.
17.证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠FDN=∠EBM,
∵E、F分别是BC、AD的中点,
∴DF=BE,
∵O是BD的中点,
∴OD=OB,
∵M、N分别是OB、OD中点,
∴DN=BM,
在△DNF和△BME中,,
∴△DNF≌△BME(SAS),
∴FN=EM,∠DNF=∠BME,
∴∠FNM=∠EMN,
∴FN∥EM,
∴四边形MENF是平行四边形.
18.(1)证明:∵BE平分∠ABC,BC=EC,
∴∠ABF=∠CBE,∠CBE=∠E,
∴∠ABF=∠E,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD为平行四边形;
(2)解:由(1)得:四边形ABCD为平行四边形,
∴AD=BC=2,
∵F为AD中点,
∴AF=DF=,
在△ABF和△DEF中,,
∴△ABF≌△DEF(AAS),
∴BF=EF=6,AB=DE,
∵AB=CD,
∴AB=CD=DE=CE=BC=,
∵FG⊥AB,
∴∠G=90°,
∴GF2=AF2﹣AG2=BF2﹣BG2,
即()2﹣AG2=62﹣(+AG)2,
解得:AG=,
∴GF==.
