18.2.2菱形的判断课件(24张)
文档属性
| 名称 | 18.2.2菱形的判断课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 146.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 19:59:42 | ||
图片预览






文档简介
第十八章 平行四边形
菱形的判定
学习目标
1.能从研究菱形性质的逆命题正确性中得到菱形的判定.
2.能运用菱形的判定方法判定一个四边形是菱形.
重点:菱形的判定的推导与归纳.
难点:菱形的判定的正确运用.
菱形的性质
边
对角线
角
菱形的性质
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分, 每一条对角线平分一组对角。
温故而知新
与研究平行四边形、矩形的判定方法相似,我们研究菱形的性质定理得逆命题,看看他们是否成立?
类比
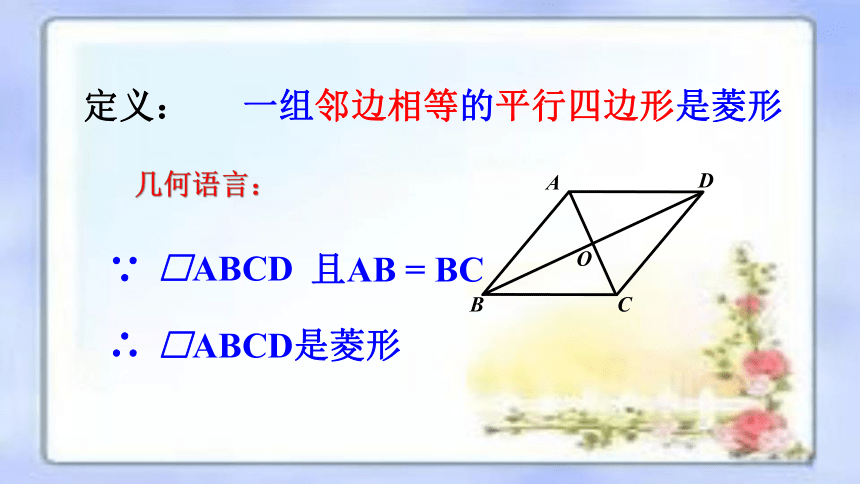
一组邻边相等的平行四边形是菱形
定义:
几何语言:
A
B
C
D
O
□ABCD
∵
∴
且AB = BC
□ABCD是菱形
菱形的四条边相等
菱形的两条对角线互相垂直平分,
逆定理
逆定理
对角线互相垂直的
平行四边形是菱形.
四条边相等的四边形是菱形
说出菱形的性质的逆定理:
猜想下面命题成立:
对角线互相垂直的平行四边形是菱形
四条边都相等的四边形是菱形
证明猜想
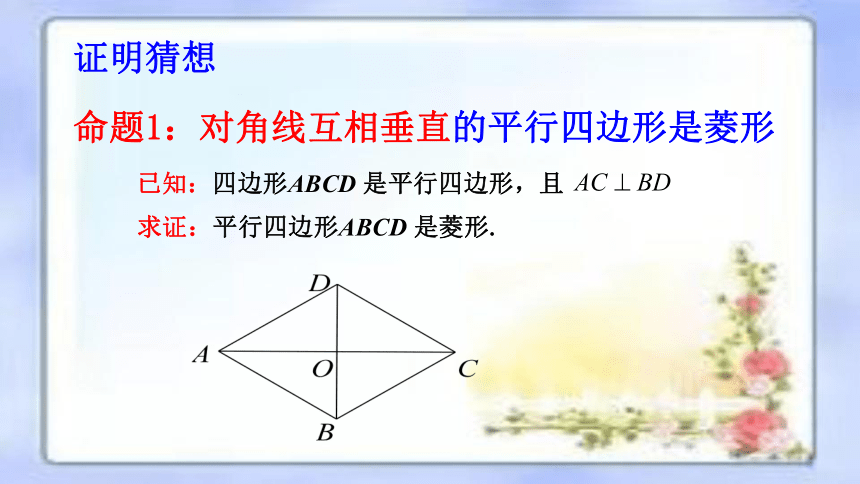
命题1:对角线互相垂直的平行四边形是菱形
已知:四边形ABCD 是平行四边形,且
求证:平行四边形ABCD 是菱形.
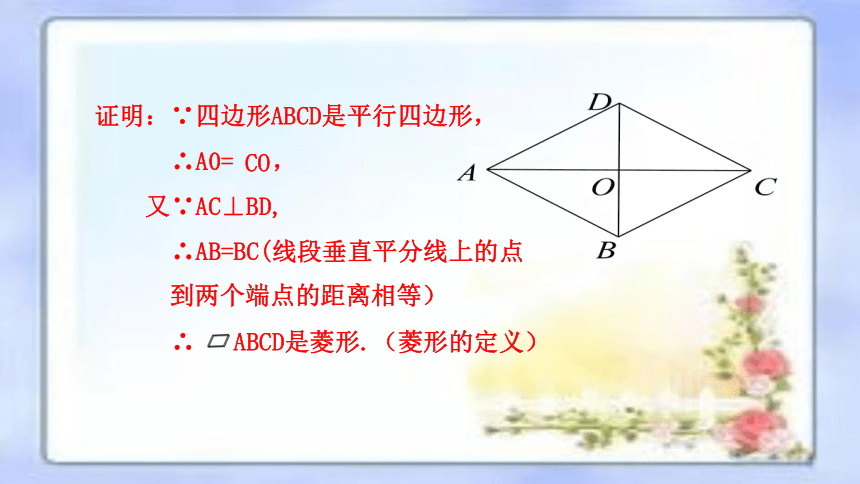
证明:∵四边形ABCD是平行四边形,
∴A0= ,
又∵AC⊥BD,
∴AB=BC(线段垂直平分线上的点
∴ ABCD是菱形.(菱形的定义)
CO
到两个端点的距离相等)
文字表达:对角线互相垂直的平行四边形是菱形
∵在□ABCD 且 AC ⊥ BD
∴□ABCD是菱形
几何语言:
例 如图, ABCD的对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证: ABCD是菱形.
针对练习
证明:∵AB=5,AO=4,BO=3,
∴AB2=AO2+BO2.
∴△OAB是直角三角形, AC⊥ BD.
∴ ABCD是菱形.
证明猜想
命题2:四条边都相等的四边形是菱形
已知:四边形ABCD中,
AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
文字表达:四条边都相等的四边形是菱形
∵AB=BC=CD=AD.
∴四边形ABCD是菱形.
几何语言:
针对练习
3.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BO平分∠ABC,且交AE于点D,连接CD,求证:四边形ABCD是菱形.
证明:
∵AE∥BF,
∴∠EAC=∠ACB.
又∵AC平分∠BAD,
∴∠ACB=∠BAC=∠EAC,
∴AB=BC.
同理:AB=AD,
∴AD=BC,而AD∥BC.
∴四边形ABCD是平行四边形.又AB=AD,
∴平行四边形ABCD是菱形.
随堂练习
1. 如图所示,下列条件中能说明四边形ABCD是菱形的有( )
A
B
C
D
O
②OA=OC,OB=OD,AB=BC;
①BD⊥AC
③AC=BD,
④AB=BC,AB∥CD
A.① B. ① ② C. ② D ③④
C
2、判断题,对的画“√”错的画“×”
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
×
√
×
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形.( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形.( )
×
√
√
2
3、 如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,EF = ED.
求证:四边形CDEF是菱形.
A
C
B
E
D
F
1
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理 △ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,
∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
2
A
C
B
E
D
F
1
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
菱形的判定定理
课堂小结
谢谢观看
菱形的判定
学习目标
1.能从研究菱形性质的逆命题正确性中得到菱形的判定.
2.能运用菱形的判定方法判定一个四边形是菱形.
重点:菱形的判定的推导与归纳.
难点:菱形的判定的正确运用.
菱形的性质
边
对角线
角
菱形的性质
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分, 每一条对角线平分一组对角。
温故而知新
与研究平行四边形、矩形的判定方法相似,我们研究菱形的性质定理得逆命题,看看他们是否成立?
类比
一组邻边相等的平行四边形是菱形
定义:
几何语言:
A
B
C
D
O
□ABCD
∵
∴
且AB = BC
□ABCD是菱形
菱形的四条边相等
菱形的两条对角线互相垂直平分,
逆定理
逆定理
对角线互相垂直的
平行四边形是菱形.
四条边相等的四边形是菱形
说出菱形的性质的逆定理:
猜想下面命题成立:
对角线互相垂直的平行四边形是菱形
四条边都相等的四边形是菱形
证明猜想
命题1:对角线互相垂直的平行四边形是菱形
已知:四边形ABCD 是平行四边形,且
求证:平行四边形ABCD 是菱形.
证明:∵四边形ABCD是平行四边形,
∴A0= ,
又∵AC⊥BD,
∴AB=BC(线段垂直平分线上的点
∴ ABCD是菱形.(菱形的定义)
CO
到两个端点的距离相等)
文字表达:对角线互相垂直的平行四边形是菱形
∵在□ABCD 且 AC ⊥ BD
∴□ABCD是菱形
几何语言:
例 如图, ABCD的对角线AC、BD相交于点O,AB=5,AO=4,BO=3.
求证: ABCD是菱形.
针对练习
证明:∵AB=5,AO=4,BO=3,
∴AB2=AO2+BO2.
∴△OAB是直角三角形, AC⊥ BD.
∴ ABCD是菱形.
证明猜想
命题2:四条边都相等的四边形是菱形
已知:四边形ABCD中,
AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=AD,
∴四边形ABCD是菱形
文字表达:四条边都相等的四边形是菱形
∵AB=BC=CD=AD.
∴四边形ABCD是菱形.
几何语言:
针对练习
3.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BO平分∠ABC,且交AE于点D,连接CD,求证:四边形ABCD是菱形.
证明:
∵AE∥BF,
∴∠EAC=∠ACB.
又∵AC平分∠BAD,
∴∠ACB=∠BAC=∠EAC,
∴AB=BC.
同理:AB=AD,
∴AD=BC,而AD∥BC.
∴四边形ABCD是平行四边形.又AB=AD,
∴平行四边形ABCD是菱形.
随堂练习
1. 如图所示,下列条件中能说明四边形ABCD是菱形的有( )
A
B
C
D
O
②OA=OC,OB=OD,AB=BC;
①BD⊥AC
③AC=BD,
④AB=BC,AB∥CD
A.① B. ① ② C. ② D ③④
C
2、判断题,对的画“√”错的画“×”
(1)对角线互相垂直的四边形是菱形( )
(2)一条对角线垂直另一条对角线的四边形是菱形( )
(3)对角线互相垂直且平分的四边形是菱形( )
×
√
×
(4)对角线相等的四边形是菱形( )
(5)对角线互相平分且邻边相等的四边形是菱形.( )
(6)两组对边分别平行且一组邻边相等的四边形是菱形.( )
×
√
√
2
3、 如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,EF = ED.
求证:四边形CDEF是菱形.
A
C
B
E
D
F
1
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理 △ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,
∴CD=ED=CF=EF,
∴四边形ABCD是菱形.
2
A
C
B
E
D
F
1
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
菱形的判定定理
课堂小结
谢谢观看
