第18章平行四边形复习课件(26张)
文档属性
| 名称 | 第18章平行四边形复习课件(26张) |  | |
| 格式 | pptx | ||
| 文件大小 | 298.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 19:59:53 | ||
图片预览





文档简介
第十八章
平行四边形
章末复行四边形》这章中,特殊四边形的性质与判定较多,但联系紧密,区别难分、易混,为了进一步弄清它们的联系与区别.这节课我们一起将本章知识结构、知识要点进行复习梳理.
整体框架
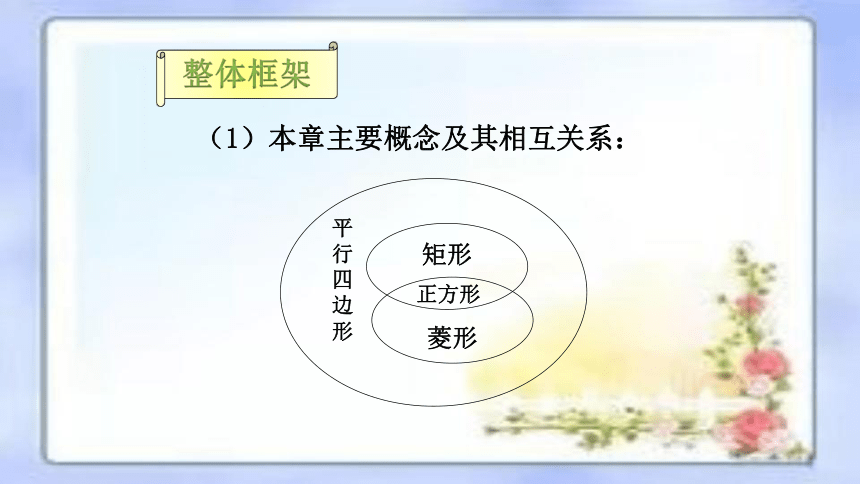
(1)本章主要概念及其相互关系:
矩形
菱形
平
行
四
边
形
正方形
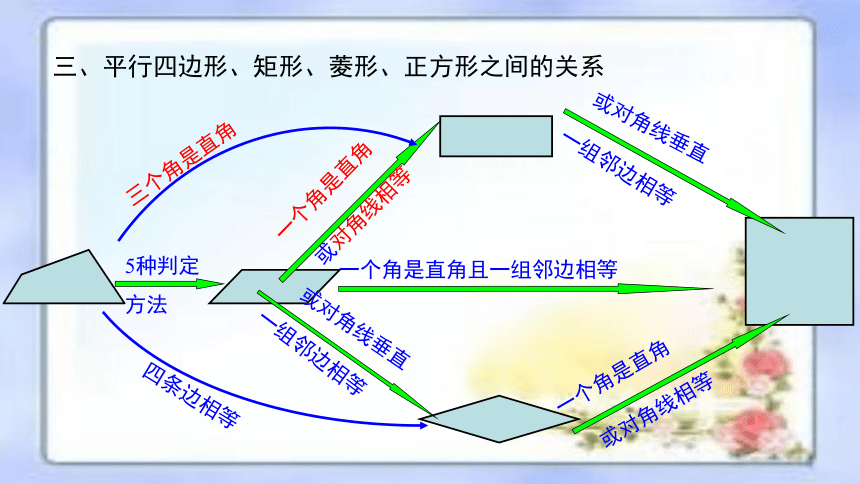
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
三、平行四边形、矩形、菱形、正方形之间的关系
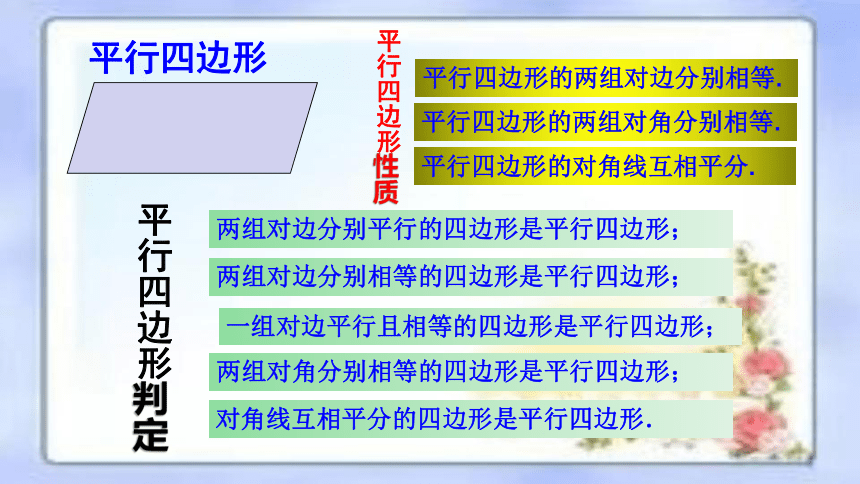
平行四边形的两组对边分别相等.
平行四边形的两组对角分别相等.
平行四边形的对角线互相平分.
对角线互相平分的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
平行四边形判定
平行四边形性质
平行四边形
直角三角形斜边上的中线等于斜边的一半.
矩形的四个角都是直角.
矩形的两条对角线相等.
矩形性质
矩形判定
对角线相等的平行四边形式矩形.
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形
菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.
菱形的四条边都相等.
菱形的对角都相等.
菱形性质
菱形
菱形判定
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
正方形性质
正方形是轴对称图形,它有四条对称轴.
正方形的四个角都是直角;
正方形的四条边都相等;
正方形的对角线相等,并且互相垂直平分;
正方形
正方形判定
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
1
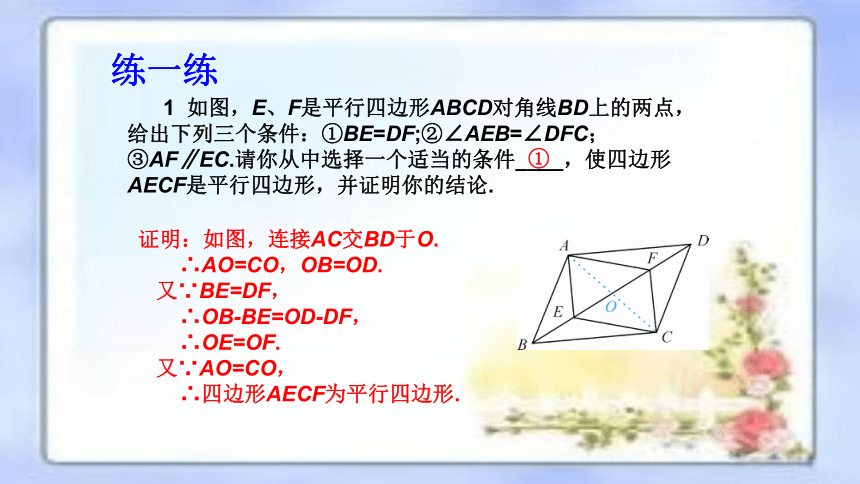
如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:①BE=DF;②∠AEB=∠DFC;③AF∥EC.请你从中选择一个适当的条件____,使四边形AECF是平行四边形,并证明你的结论.
证明:如图,连接AC交BD于O.
∴AO=CO,OB=OD.
又∵BE=DF,
∴OB-BE=OD-DF,
∴OE=OF.
又∵AO=CO,
∴四边形AECF为平行四边形.
①
练一练
如图,在平行四边形ABCD,BE⊥AD于E,若∠ABE=50°,则∠C=
。
分析:由BE⊥AD于E,∠ABE=50°,
而得∠A=40°,
由平行四边形的对角相等
知∠C=∠A=40°
40°
2
3、如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是多少?
=5,
解:∵?ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO,
∵AB⊥AC,AB=4,AC=6,
∴BO=
∴BD=2BO=10,
4.
如图,点E、F、G、H分别为四边形ABCD的边AB、BC、CD、D
A的中点,试判断四边形EFGH的形状,并证明你的结论.
解:四边形EFGH为平行四边形.
如图,连接AC,在△ACD中,H、G分别为AD、CD的中点,
∴HG∥AC,HG=
AC,
同理:EF∥AC,EF=
AC,
∴HG∥EF,HG=EF.
∴四边形EFGH为平行四边形.
5.
如图,平行四边形ABCD中,AB⊥AC,∠ABD=35°,对角线AC,BD相交于点O。将直线AC绕点O顺时针旋转,分别交BC、AD于E,F,当四边形BEDF是菱形时,直线AC绕点O顺时针至少旋转
。
35°
6.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求高DH的长.
解:∵四边形ABCD为菱形,
∴AO=
AC=4cm,AC⊥BD,
∴在Rt△AOB中,
(cm).
S△ABD=
DH
·
AB=
AO
·
BD
∴DH=
(cm).
7.
如图,矩形ABCD中,AD=2AB=4,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则DE=
。
8、在一个平行四边形中,若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少.
解:如图,∵在平行四边形ABCD中,AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE.
又∵∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE.
(1)当AE=2时,则平行四边形的周长=2(2+5)=14.
(2)当AE=3时,则平行四边形的周长=2(3+5)=16.
9.如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点,如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的四分之一,你能说明理由吗?
解:∵∠BOF+∠A′OB=90°,∠A′OB+∠AOE=90°.
∴∠BOF=∠AOE.
又∵OA=OB,∠OAE=∠OBF.
∴△AOE≌△BOF.
∴S△AOE=S△BOF
.
∴S四边形EBFO=S△BOF+S△OEB
=S△AOE+S
△OEB
=
S正方形ABCD.
10
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD的中点,点M是AB边上一动点(不与点A重合)。延长ME交射线CD于点N,连接MD,AN。
(1)求证:四边形AMDN是平行四边形;
证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME。
又∵点E是AD边的中点,
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形。
(2)①当AM为何值时,四边形AMDN是矩形;
②当AM为何值时,四边形AMDN是菱形。
解:①当AM的值为1时,四边形AMDN是矩形。
理由如下:
∵AM=1=(1/2)AD=AE=ED,
又∵∠EAM=60°,
∴△AEM为等边三角形。
∴∠AEM=60°,∠EDM=30°,
∴∠AMD=90°
,
∴四边形AMDN是矩形。
②当AM的值为2时,四边形AMDN是菱形。
理由如下:
∵AM=2,
∴AM=AD=2,
∴△AMD是等边三角形,
∴AM=DM,
∴四边形AMDN是菱形。
4、如图,ABCD为平行四边形,E、F分别为AB、CD的中点,①求证:AECF也是平行四边形;②连接BD,分别交CE、AF于G、H,求证:BG=DH;③连接CH、AG,则AGCH也是平行四边形吗?
解:
?:
∵AE∥FC且AE=FC
AD=BC
DF=EB
∠ABC=∠ADC
∴△ADF≌△CBE
(SAS)
∴AF=CE
∠DAF=∠ECB
∴四边形AECF是平行四边形
?:
∵AD∥BC
∴∠ADH=∠CBG
∴∠ADH=∠CBG
∠DAF=∠ECB
AD=BC
∴△ADH≌△CBG(ASA)
∴DH=BG
?:是平行四边形
∵DH=BG
AD=BC
∠HDA=∠GBC
∴△AHD≌△CBG(ASA)
∴AH=CG
∴同理可证得CH=AG
∴四边形AGCH是平行四边形
谢谢观看
平行四边形
章末复行四边形》这章中,特殊四边形的性质与判定较多,但联系紧密,区别难分、易混,为了进一步弄清它们的联系与区别.这节课我们一起将本章知识结构、知识要点进行复习梳理.
整体框架
(1)本章主要概念及其相互关系:
矩形
菱形
平
行
四
边
形
正方形
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
三、平行四边形、矩形、菱形、正方形之间的关系
平行四边形的两组对边分别相等.
平行四边形的两组对角分别相等.
平行四边形的对角线互相平分.
对角线互相平分的四边形是平行四边形.
两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
平行四边形判定
平行四边形性质
平行四边形
直角三角形斜边上的中线等于斜边的一半.
矩形的四个角都是直角.
矩形的两条对角线相等.
矩形性质
矩形判定
对角线相等的平行四边形式矩形.
有一个角是直角的平行四边形是矩形.
有三个角是直角的四边形是矩形.
矩形
菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角.
菱形的四条边都相等.
菱形的对角都相等.
菱形性质
菱形
菱形判定
四条边都相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有一组邻边相等的平行四边形叫做菱形.
正方形性质
正方形是轴对称图形,它有四条对称轴.
正方形的四个角都是直角;
正方形的四条边都相等;
正方形的对角线相等,并且互相垂直平分;
正方形
正方形判定
有一组邻边相等的矩形是正方形.
有一个角为直角的菱形是正方形.
1
如图,E、F是平行四边形ABCD对角线BD上的两点,给出下列三个条件:①BE=DF;②∠AEB=∠DFC;③AF∥EC.请你从中选择一个适当的条件____,使四边形AECF是平行四边形,并证明你的结论.
证明:如图,连接AC交BD于O.
∴AO=CO,OB=OD.
又∵BE=DF,
∴OB-BE=OD-DF,
∴OE=OF.
又∵AO=CO,
∴四边形AECF为平行四边形.
①
练一练
如图,在平行四边形ABCD,BE⊥AD于E,若∠ABE=50°,则∠C=
。
分析:由BE⊥AD于E,∠ABE=50°,
而得∠A=40°,
由平行四边形的对角相等
知∠C=∠A=40°
40°
2
3、如图,?ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是多少?
=5,
解:∵?ABCD的对角线AC与BD相交于点O,
∴BO=DO,AO=CO,
∵AB⊥AC,AB=4,AC=6,
∴BO=
∴BD=2BO=10,
4.
如图,点E、F、G、H分别为四边形ABCD的边AB、BC、CD、D
A的中点,试判断四边形EFGH的形状,并证明你的结论.
解:四边形EFGH为平行四边形.
如图,连接AC,在△ACD中,H、G分别为AD、CD的中点,
∴HG∥AC,HG=
AC,
同理:EF∥AC,EF=
AC,
∴HG∥EF,HG=EF.
∴四边形EFGH为平行四边形.
5.
如图,平行四边形ABCD中,AB⊥AC,∠ABD=35°,对角线AC,BD相交于点O。将直线AC绕点O顺时针旋转,分别交BC、AD于E,F,当四边形BEDF是菱形时,直线AC绕点O顺时针至少旋转
。
35°
6.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求高DH的长.
解:∵四边形ABCD为菱形,
∴AO=
AC=4cm,AC⊥BD,
∴在Rt△AOB中,
(cm).
S△ABD=
DH
·
AB=
AO
·
BD
∴DH=
(cm).
7.
如图,矩形ABCD中,AD=2AB=4,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则DE=
。
8、在一个平行四边形中,若一个角的平分线把一条边分成长是2cm和3cm的两条线段,求该平行四边形的周长是多少.
解:如图,∵在平行四边形ABCD中,AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE.
又∵∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE.
(1)当AE=2时,则平行四边形的周长=2(2+5)=14.
(2)当AE=3时,则平行四边形的周长=2(3+5)=16.
9.如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点,如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的四分之一,你能说明理由吗?
解:∵∠BOF+∠A′OB=90°,∠A′OB+∠AOE=90°.
∴∠BOF=∠AOE.
又∵OA=OB,∠OAE=∠OBF.
∴△AOE≌△BOF.
∴S△AOE=S△BOF
.
∴S四边形EBFO=S△BOF+S△OEB
=S△AOE+S
△OEB
=
S正方形ABCD.
10
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD的中点,点M是AB边上一动点(不与点A重合)。延长ME交射线CD于点N,连接MD,AN。
(1)求证:四边形AMDN是平行四边形;
证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME。
又∵点E是AD边的中点,
∴DE=AE,
∴△NDE≌△MAE,
∴ND=MA,
∴四边形AMDN是平行四边形。
(2)①当AM为何值时,四边形AMDN是矩形;
②当AM为何值时,四边形AMDN是菱形。
解:①当AM的值为1时,四边形AMDN是矩形。
理由如下:
∵AM=1=(1/2)AD=AE=ED,
又∵∠EAM=60°,
∴△AEM为等边三角形。
∴∠AEM=60°,∠EDM=30°,
∴∠AMD=90°
,
∴四边形AMDN是矩形。
②当AM的值为2时,四边形AMDN是菱形。
理由如下:
∵AM=2,
∴AM=AD=2,
∴△AMD是等边三角形,
∴AM=DM,
∴四边形AMDN是菱形。
4、如图,ABCD为平行四边形,E、F分别为AB、CD的中点,①求证:AECF也是平行四边形;②连接BD,分别交CE、AF于G、H,求证:BG=DH;③连接CH、AG,则AGCH也是平行四边形吗?
解:
?:
∵AE∥FC且AE=FC
AD=BC
DF=EB
∠ABC=∠ADC
∴△ADF≌△CBE
(SAS)
∴AF=CE
∠DAF=∠ECB
∴四边形AECF是平行四边形
?:
∵AD∥BC
∴∠ADH=∠CBG
∴∠ADH=∠CBG
∠DAF=∠ECB
AD=BC
∴△ADH≌△CBG(ASA)
∴DH=BG
?:是平行四边形
∵DH=BG
AD=BC
∠HDA=∠GBC
∴△AHD≌△CBG(ASA)
∴AH=CG
∴同理可证得CH=AG
∴四边形AGCH是平行四边形
谢谢观看
