7.1.2 平面直角坐标系(2)课件(共16张PPT)
文档属性
| 名称 | 7.1.2 平面直角坐标系(2)课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 09:09:15 | ||
图片预览



文档简介
7.1.2 平面直角坐标系(2)
2021年春人教版七年级(下)数学
第七章 平面直角坐标系
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
5
-2
-3
-4
-1
3
2
4
1
6
y
y轴或纵轴
x轴或横轴
原点
第一象限
第二象限
第三象限
第四象限
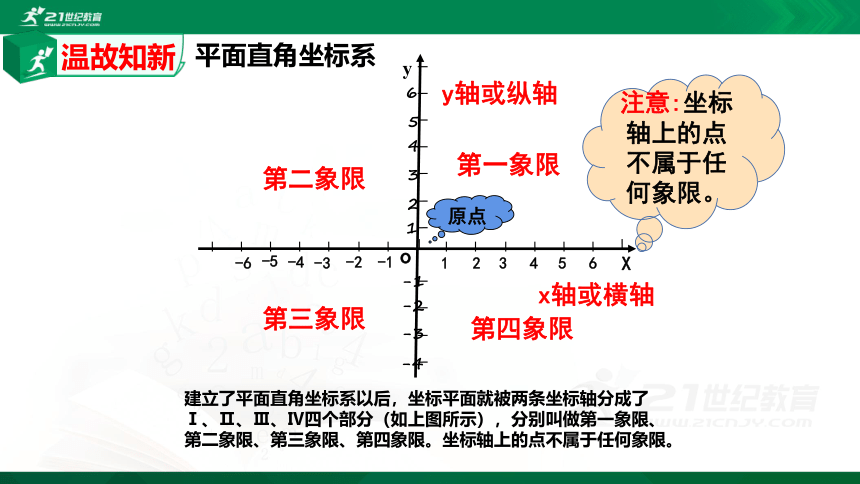
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成了
Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分(如上图所示),分别叫做第一象限、
第二象限、第三象限、第四象限。坐标轴上的点不属于任何象限。
注意:坐标轴上的点不属于任何象限。
平面直角坐标系
温故知新
根据点所在位置,用“+” “-”或“0”添表
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在正半轴上
在x轴上
在负半轴上
在正半轴上
在y轴上
在负半轴上
原点
-
-
-
-
+
+
+
0
0
-
-
0
0
+
0
0
+
+
y
x
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
0
A
D
C
B
(3,4)
(-3,4)
(-3,-4)
(3,-4)
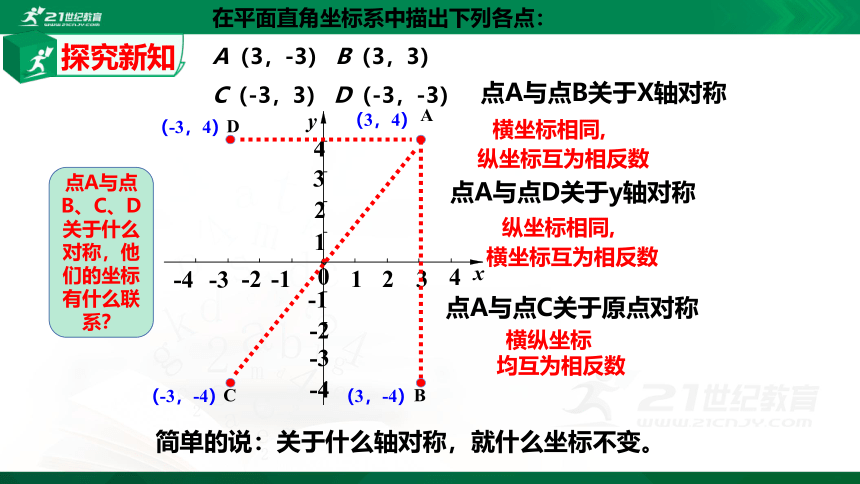
点A与点B关于X轴对称
点A与点D关于y轴对称
点A与点C关于原点对称
横坐标相同,
纵坐标互为相反数
纵坐标相同,
横坐标互为相反数
横纵坐标
均互为相反数
简单的说:关于什么轴对称,就什么坐标不变。
在平面直角坐标系中描出下列各点:
A(3,-3) B(3,3)
C(-3,3) D(-3,-3)
点A与点B、C、D关于什么对称,他们的坐标有什么联系?
探究新知
归纳:
(1)关于x轴对称的两点,横坐标相等,纵坐标互为相反数.如A(3,-3)和 B(3,3)
(2)关于y轴对称的两点,纵坐标相等,横坐标互为相反数.如C(-3,3)和 B(3,3)
(3)关于原点对称的两点,横纵坐标分别互为相反数.如C(-3,3)和A(3,-3)
B(3,3)和 D(-3,-3)
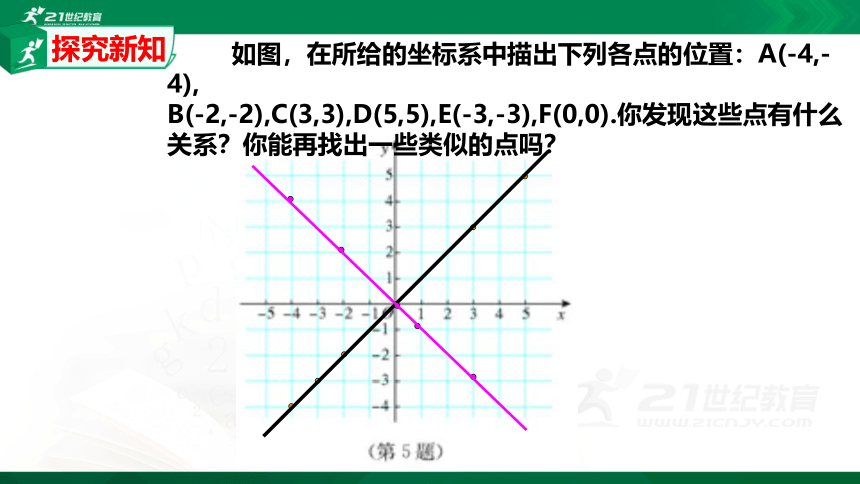
如图,在所给的坐标系中描出下列各点的位置:A(-4,-4),
B(-2,-2),C(3,3),D(5,5),E(-3,-3),F(0,0).你发现这些点有什么关系?你能再找出一些类似的点吗?
探究新知
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
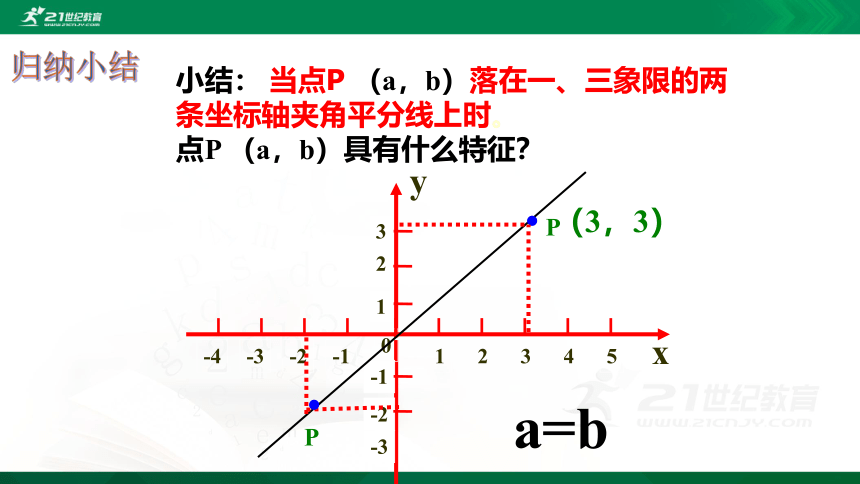
小结: 当点P (a,b)落在一、三象限的两 条坐标轴夹角平分线上时。
点P (a,b)具有什么特征?
x
y
(3,3)
·
P
·
P
a=b
归纳小结
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
P
·
P
( - 3,3)
a=-b
小结: 当点P (a,b)落在二、四象限的两 条坐标轴夹角平分线上时。
点P (a,b)具有什么特征?
归纳小结
y
x
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
0
A
B
C
D
点A、B、C、D四点到X轴、y轴的距离是多少?你发现了什么规律?
(3,4)
(-2,4)
(-2,-3)
(3,-3)
点P(x,y)到X轴的距离是∣y∣
点P(x,y)到y轴的距离是∣x∣
点A、B的纵坐标有什么特点?直线AB与X轴有怎样的位置关系?由此发现什么规律?点A和点D呢?
纵坐标相同的点的连线平行于X轴
横坐标相同的点的连线平行于y轴
归纳小结
1. 在平面直角坐标系中点A(-1,0)位于( )
A.第二象限 B. x轴的负半轴上
C.第三象限 D.y轴的负半轴上
B
2.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.以上都不对
B
课堂练习
4.点P (-3,4) 关于x轴的对称点的坐标为__________;关于y轴的对称点的坐标为__________;关于原点的对称点的坐标为__________。
3. 若点B(n+4,n-1)在y轴上,则n=______。
-4
(-3,-4)
(3,4)
(3,-4)
3
2
5
-3
-5
3
5.若点A(x,3)在第一象限的角平分线上,则x=______.
6.若点B(-2,y)在第二象限的角平分线上,则y=_______.
7.已知点M(-3,b),N(a,5):
(1)若点M、N两点都在第一、三象限角平分线上,则a=___,b=____.
(2)若点M、N两点都在第二、四象限角平分线上,则a=___,b=____.
8.坐标平面内点P(m,2)与点Q(3,-2)关于原点对称,则m= _______.
9.已知,点A(3a+5,-6a-2)在第二四象限的角平分线上,求a2005-a的值
-3
解:∵点A(3a+5,-6a-2)在第二四象限的角平分线上,
∴(3a+5)+(-6a-2)=0
解得:a=1
∴a2005-a=12005-1=0
11,如果∣3x+2∣+∣2y-1∣=0,那么点P(x,y)和Q(x+1,y-2)分别在哪个象限?
10.若点P(x,y)满足xy﹥0,则点p在第几象限?
解:∵xy﹥0
∴x、y同号
∴点p在第一象限或第三象限。
解:∵∣3x+2∣≥0,∣2y-1∣≥0
又∣3x+2∣+∣2y-1∣=0
∴3x+2=0,2y-1=0
解得:x= ,y=
∴P( , ), Q( )分别在第二、四象限。
点P(x ,y)
“三”大特征:
原点坐标:
x轴上的点:
y轴上的点:
(0,0)
纵坐标等于0
横坐标等于0
“三”个对称:
点P(x ,y)
关于y轴的对称点:
关于原点的对称点:
关于x轴的对称点:
P1 (x , -y)
P2 (- x, y)
P3 (- x , -y)
“两”个距离:
到x轴的距离 =
到y轴的距离 =
∣y∣
∣x ∣
“两”个平行:
与x轴平行线上的点:
与y轴平行线上的点:
纵坐标相同
横坐标相同
“两”个平分:
一三象限角平分线上的点:
二四象限角平分线上的点:
x =y
x +y=0
课堂小结
2021年春人教版七年级(下)数学
第七章 平面直角坐标系
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
5
-2
-3
-4
-1
3
2
4
1
6
y
y轴或纵轴
x轴或横轴
原点
第一象限
第二象限
第三象限
第四象限
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成了
Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分(如上图所示),分别叫做第一象限、
第二象限、第三象限、第四象限。坐标轴上的点不属于任何象限。
注意:坐标轴上的点不属于任何象限。
平面直角坐标系
温故知新
根据点所在位置,用“+” “-”或“0”添表
点的位置
横坐标符号
纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在正半轴上
在x轴上
在负半轴上
在正半轴上
在y轴上
在负半轴上
原点
-
-
-
-
+
+
+
0
0
-
-
0
0
+
0
0
+
+
y
x
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
0
A
D
C
B
(3,4)
(-3,4)
(-3,-4)
(3,-4)
点A与点B关于X轴对称
点A与点D关于y轴对称
点A与点C关于原点对称
横坐标相同,
纵坐标互为相反数
纵坐标相同,
横坐标互为相反数
横纵坐标
均互为相反数
简单的说:关于什么轴对称,就什么坐标不变。
在平面直角坐标系中描出下列各点:
A(3,-3) B(3,3)
C(-3,3) D(-3,-3)
点A与点B、C、D关于什么对称,他们的坐标有什么联系?
探究新知
归纳:
(1)关于x轴对称的两点,横坐标相等,纵坐标互为相反数.如A(3,-3)和 B(3,3)
(2)关于y轴对称的两点,纵坐标相等,横坐标互为相反数.如C(-3,3)和 B(3,3)
(3)关于原点对称的两点,横纵坐标分别互为相反数.如C(-3,3)和A(3,-3)
B(3,3)和 D(-3,-3)
如图,在所给的坐标系中描出下列各点的位置:A(-4,-4),
B(-2,-2),C(3,3),D(5,5),E(-3,-3),F(0,0).你发现这些点有什么关系?你能再找出一些类似的点吗?
探究新知
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
小结: 当点P (a,b)落在一、三象限的两 条坐标轴夹角平分线上时。
点P (a,b)具有什么特征?
x
y
(3,3)
·
P
·
P
a=b
归纳小结
3
1
2
-2
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
·
P
·
P
( - 3,3)
a=-b
小结: 当点P (a,b)落在二、四象限的两 条坐标轴夹角平分线上时。
点P (a,b)具有什么特征?
归纳小结
y
x
1
2
3
4
1
2
3
4
-1
-2
-3
-4
-1
-2
-3
-4
0
A
B
C
D
点A、B、C、D四点到X轴、y轴的距离是多少?你发现了什么规律?
(3,4)
(-2,4)
(-2,-3)
(3,-3)
点P(x,y)到X轴的距离是∣y∣
点P(x,y)到y轴的距离是∣x∣
点A、B的纵坐标有什么特点?直线AB与X轴有怎样的位置关系?由此发现什么规律?点A和点D呢?
纵坐标相同的点的连线平行于X轴
横坐标相同的点的连线平行于y轴
归纳小结
1. 在平面直角坐标系中点A(-1,0)位于( )
A.第二象限 B. x轴的负半轴上
C.第三象限 D.y轴的负半轴上
B
2.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( )
A.平行于x轴 B.平行于y轴
C.经过原点 D.以上都不对
B
课堂练习
4.点P (-3,4) 关于x轴的对称点的坐标为__________;关于y轴的对称点的坐标为__________;关于原点的对称点的坐标为__________。
3. 若点B(n+4,n-1)在y轴上,则n=______。
-4
(-3,-4)
(3,4)
(3,-4)
3
2
5
-3
-5
3
5.若点A(x,3)在第一象限的角平分线上,则x=______.
6.若点B(-2,y)在第二象限的角平分线上,则y=_______.
7.已知点M(-3,b),N(a,5):
(1)若点M、N两点都在第一、三象限角平分线上,则a=___,b=____.
(2)若点M、N两点都在第二、四象限角平分线上,则a=___,b=____.
8.坐标平面内点P(m,2)与点Q(3,-2)关于原点对称,则m= _______.
9.已知,点A(3a+5,-6a-2)在第二四象限的角平分线上,求a2005-a的值
-3
解:∵点A(3a+5,-6a-2)在第二四象限的角平分线上,
∴(3a+5)+(-6a-2)=0
解得:a=1
∴a2005-a=12005-1=0
11,如果∣3x+2∣+∣2y-1∣=0,那么点P(x,y)和Q(x+1,y-2)分别在哪个象限?
10.若点P(x,y)满足xy﹥0,则点p在第几象限?
解:∵xy﹥0
∴x、y同号
∴点p在第一象限或第三象限。
解:∵∣3x+2∣≥0,∣2y-1∣≥0
又∣3x+2∣+∣2y-1∣=0
∴3x+2=0,2y-1=0
解得:x= ,y=
∴P( , ), Q( )分别在第二、四象限。
点P(x ,y)
“三”大特征:
原点坐标:
x轴上的点:
y轴上的点:
(0,0)
纵坐标等于0
横坐标等于0
“三”个对称:
点P(x ,y)
关于y轴的对称点:
关于原点的对称点:
关于x轴的对称点:
P1 (x , -y)
P2 (- x, y)
P3 (- x , -y)
“两”个距离:
到x轴的距离 =
到y轴的距离 =
∣y∣
∣x ∣
“两”个平行:
与x轴平行线上的点:
与y轴平行线上的点:
纵坐标相同
横坐标相同
“两”个平分:
一三象限角平分线上的点:
二四象限角平分线上的点:
x =y
x +y=0
课堂小结
