2020-2021学年七年级数学沪科版下册8.3 第1课时 完全平方公式 课件(共20张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学沪科版下册8.3 第1课时 完全平方公式 课件(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 279.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 21:40:43 | ||
图片预览








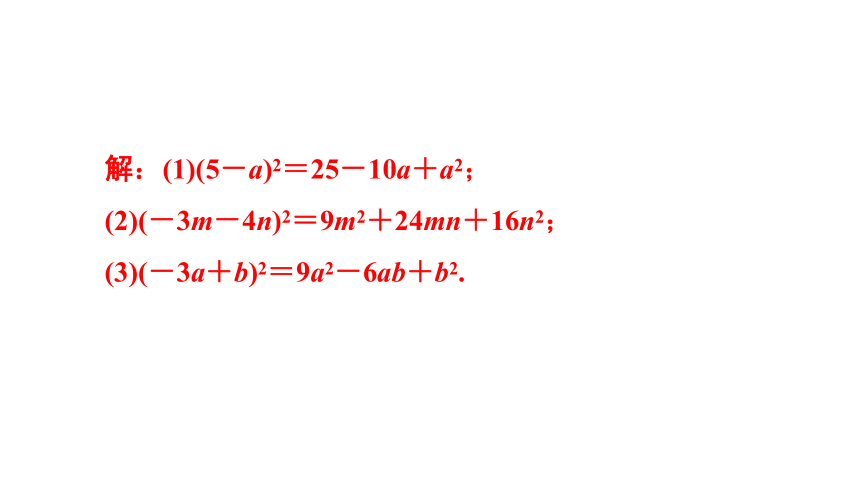
文档简介
第八章 整式乘法与因式分解
8.3 完全平方公式与平方差公式
第1课时 完全平方公式
1.通过实际问题情境,探究完全平方式;
2.熟练运用完全平方式,进行运算;
3.培养学生自主探究和运算的能力,增强学生应用整体思想解决问题的意识.
学习目标
课堂导入
请同学们用多项式与多项式的乘法法则做一做
( a + b) 2= ( a + b ) ( a+b )=
a?a+a?b+b?a+b?b=a2+2ab+b2
( a – b )2= ( a – b ) ( a – b ) =
a?a-a?b-b?a+b?b=a2-2ab+b2
课堂导入
观察以上算式及运算结果,你发现了什么规律?
( a + b) 2= ( a + b ) ( a+b )=a?a+a?b+b?a+b?b=a2+2ab+b2
( a – b )2= ( a – b ) ( a – b ) =a?a-a?b-b?a+b?b=a2-2ab+b2
新知讲解
1. 完全平方式
(a+b)2= a2+2ab+b2
(a-b)2= a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫作完全平方公式.
新知讲解
完全平方公式:(a±b)2=a2±2ab+b2.可巧记为“首平方,末平方,首末两倍中间放”.
新知讲解
公式特征:
1.积为二次三项式;
2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同.
4.公式中的字母a,b可以表示数,单项式和多项式.
2. 完全平方式的计算
新知讲解
利用完全平方公式计算:
(1)(5-a)2;
(2)(-3m-4n)2;
(3)(-3a+b)2.
新知讲解
解:(1)(5-a)2=25-10a+a2;
(2)(-3m-4n)2=9m2+24mn+16n2;
(3)(-3a+b)2=9a2-6ab+b2.
巩固练习:下列计算是否正确.
(2x+y)2=4x2+y2
(3a-2b)2=9a2-4b2
(1-3m)(1+3m)=1-3m2
新知讲解
×
×
×
(2x+y)2=(2x)2+2(2x)y+y2=4x2+4xy+y2
(3a-2b)2=9a2-12ab+4b2
(1-3m)(1+3m)==1 - 9m2
3. 完全平方式的实际应用
新知讲解
如果36x2+(m+1)xy+25y2是一个完全平方式,求m的值.
解:∵36x2+(m+1)xy+25y2=(6x)2+(m+1)xy+(5y)2,∴(m+1)xy=±2·6x·5y,∴m+1=±60,∴m=59或-61.
典型例题
例1 若(x+y)2=9,且(x-y)2=1.
(1)求????????????+????????????的值;
(2)求(x2+1)(y2+1)的值.
所求的展开式中都含有xy或x+y时,我们可以把它们看作一个整体代入到需要求值的代数式中,整体求解.
?
典型例题
解:
(1)∵(x+y)2=9,(x-y)2=1,∴x2+2xy+y2=9,x2-2xy+y2=1,4xy=9-1=8,∴xy=2,
∴ ????????????+?????????????=????????+????????????????????????=????+?????????????????????????????????????=????????;
(2)∵(x+y)2=9,xy=2,∴(x2+1)(y2+1)=x2y2+y2+x2+1=x2y2+(x+y)2-2xy+1=22+9-2×2+1=10.
?
随堂练习
1.计算:运用乘法公式计算: (a+b-5)2.
解:原式= [(a+b)-5]2
= (a+b)2-10(a+b)+52
= a2+2ab+b2-10a-10b+25
随堂练习
2.思考:怎样计算1022更简便呢?
解:原式= (100+2)2
=10000+400+4
=10404.
随堂练习
3.若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
解:a2+b2=(a+b)2-2ab=52-2×(-6)=37;
a2-ab+b2=a2+b2-ab=37-(-6)=43.
随堂练习
4.已知x2+y2=8,x+y=4,求x-y.
解:∵x+y=4, ∴(x+y)2=16,即x2+y2+2xy=16;
∵x2+y2=8;
得2xy=8,
得x2+y2-2xy=0.即(x-y)2=0,故x-y=0
课堂小结
1. 完全平方公式
(a+b)2= a2+2ab+b2
(a-b)2= a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫作完全平方公式.
课堂小结
公式特征:
1.积为二次三项式;
2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同.
4.公式中的字母a,b可以表示数,单项式和多项式.
再 见
8.3 完全平方公式与平方差公式
第1课时 完全平方公式
1.通过实际问题情境,探究完全平方式;
2.熟练运用完全平方式,进行运算;
3.培养学生自主探究和运算的能力,增强学生应用整体思想解决问题的意识.
学习目标
课堂导入
请同学们用多项式与多项式的乘法法则做一做
( a + b) 2= ( a + b ) ( a+b )=
a?a+a?b+b?a+b?b=a2+2ab+b2
( a – b )2= ( a – b ) ( a – b ) =
a?a-a?b-b?a+b?b=a2-2ab+b2
课堂导入
观察以上算式及运算结果,你发现了什么规律?
( a + b) 2= ( a + b ) ( a+b )=a?a+a?b+b?a+b?b=a2+2ab+b2
( a – b )2= ( a – b ) ( a – b ) =a?a-a?b-b?a+b?b=a2-2ab+b2
新知讲解
1. 完全平方式
(a+b)2= a2+2ab+b2
(a-b)2= a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫作完全平方公式.
新知讲解
完全平方公式:(a±b)2=a2±2ab+b2.可巧记为“首平方,末平方,首末两倍中间放”.
新知讲解
公式特征:
1.积为二次三项式;
2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同.
4.公式中的字母a,b可以表示数,单项式和多项式.
2. 完全平方式的计算
新知讲解
利用完全平方公式计算:
(1)(5-a)2;
(2)(-3m-4n)2;
(3)(-3a+b)2.
新知讲解
解:(1)(5-a)2=25-10a+a2;
(2)(-3m-4n)2=9m2+24mn+16n2;
(3)(-3a+b)2=9a2-6ab+b2.
巩固练习:下列计算是否正确.
(2x+y)2=4x2+y2
(3a-2b)2=9a2-4b2
(1-3m)(1+3m)=1-3m2
新知讲解
×
×
×
(2x+y)2=(2x)2+2(2x)y+y2=4x2+4xy+y2
(3a-2b)2=9a2-12ab+4b2
(1-3m)(1+3m)==1 - 9m2
3. 完全平方式的实际应用
新知讲解
如果36x2+(m+1)xy+25y2是一个完全平方式,求m的值.
解:∵36x2+(m+1)xy+25y2=(6x)2+(m+1)xy+(5y)2,∴(m+1)xy=±2·6x·5y,∴m+1=±60,∴m=59或-61.
典型例题
例1 若(x+y)2=9,且(x-y)2=1.
(1)求????????????+????????????的值;
(2)求(x2+1)(y2+1)的值.
所求的展开式中都含有xy或x+y时,我们可以把它们看作一个整体代入到需要求值的代数式中,整体求解.
?
典型例题
解:
(1)∵(x+y)2=9,(x-y)2=1,∴x2+2xy+y2=9,x2-2xy+y2=1,4xy=9-1=8,∴xy=2,
∴ ????????????+?????????????=????????+????????????????????????=????+?????????????????????????????????????=????????;
(2)∵(x+y)2=9,xy=2,∴(x2+1)(y2+1)=x2y2+y2+x2+1=x2y2+(x+y)2-2xy+1=22+9-2×2+1=10.
?
随堂练习
1.计算:运用乘法公式计算: (a+b-5)2.
解:原式= [(a+b)-5]2
= (a+b)2-10(a+b)+52
= a2+2ab+b2-10a-10b+25
随堂练习
2.思考:怎样计算1022更简便呢?
解:原式= (100+2)2
=10000+400+4
=10404.
随堂练习
3.若a+b=5,ab=-6, 求a2+b2,a2-ab+b2.
解:a2+b2=(a+b)2-2ab=52-2×(-6)=37;
a2-ab+b2=a2+b2-ab=37-(-6)=43.
随堂练习
4.已知x2+y2=8,x+y=4,求x-y.
解:∵x+y=4, ∴(x+y)2=16,即x2+y2+2xy=16;
∵x2+y2=8;
得2xy=8,
得x2+y2-2xy=0.即(x-y)2=0,故x-y=0
课堂小结
1. 完全平方公式
(a+b)2= a2+2ab+b2
(a-b)2= a2-2ab+b2
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍.这两个公式叫作完全平方公式.
课堂小结
公式特征:
1.积为二次三项式;
2.积中的两项为两数的平方;
3.另一项是两数积的2倍,且与乘式中间的符号相同.
4.公式中的字母a,b可以表示数,单项式和多项式.
再 见
