北师大版八年级数学下册 第一章《三角形的证明》角平分线 解答题专项(三)(Word版含答案)
文档属性
| 名称 | 北师大版八年级数学下册 第一章《三角形的证明》角平分线 解答题专项(三)(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 286.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览


文档简介
北师大版八年级数学下册第一章《三角形的证明》
角平分线解答题专项(三)
1.如图,△ABC中,∠C=60°,AD,BE分别平分∠CAB,∠CBA、AD、BE交于点P.求证:
(1)∠APB=120°;
(2)点P在∠C的平分线上;
(3)AB=AE+BD.
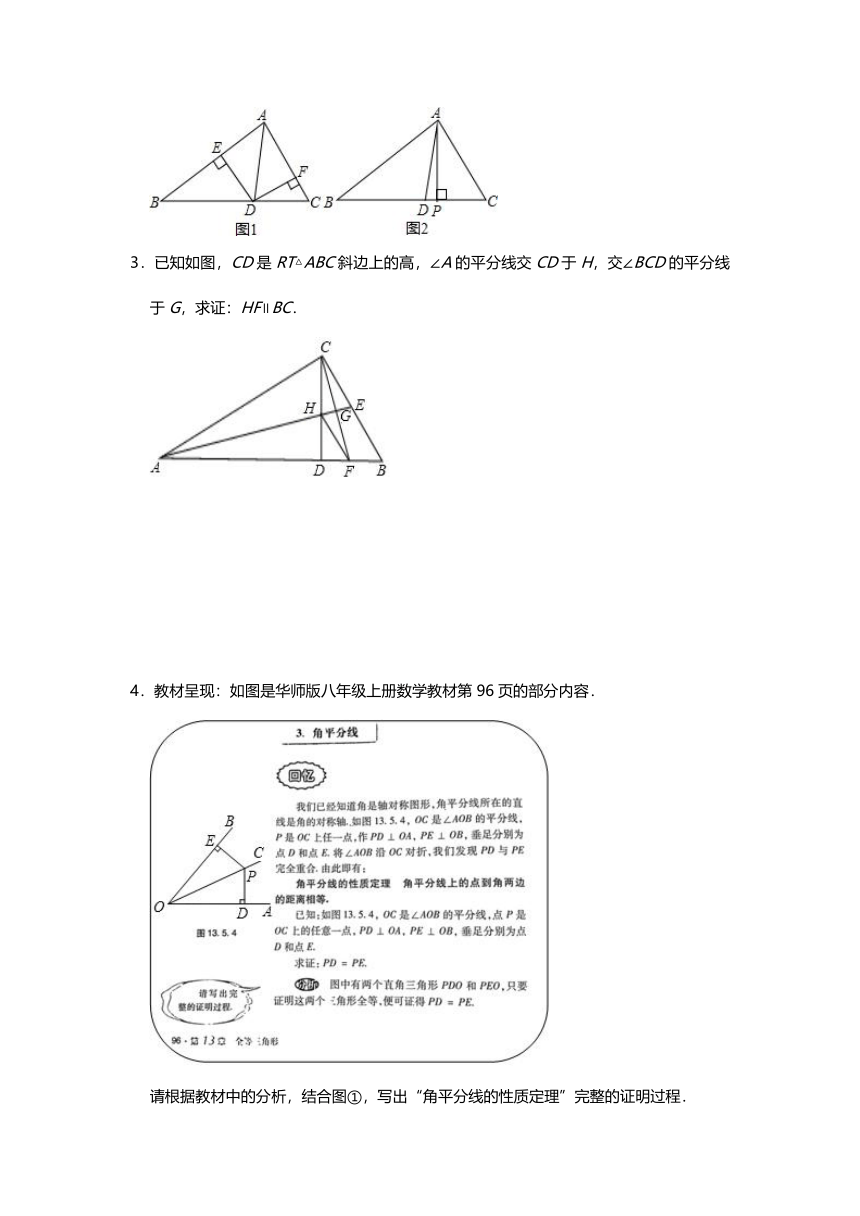
2.如图,已知△ABC中,AD平分∠BAC.
(1)在图1中,作DE⊥AB,DF⊥AC,
∵AD平分∠BAC,∴ = ,
而S△ABD= × ,
S△ACD= ×
则S△ABD:S△ACD= :
(2)在图2中,作AP⊥BC而 × , × ,
则S△ABD:S△ACD= : ;
(3)由(1)、(2)可得“角平分线”第二性质 : = : .
3.已知如图,CD是RT△ABC斜边上的高,∠A的平分线交CD于H,交∠BCD的平分线于G,求证:HF∥BC.
4.教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
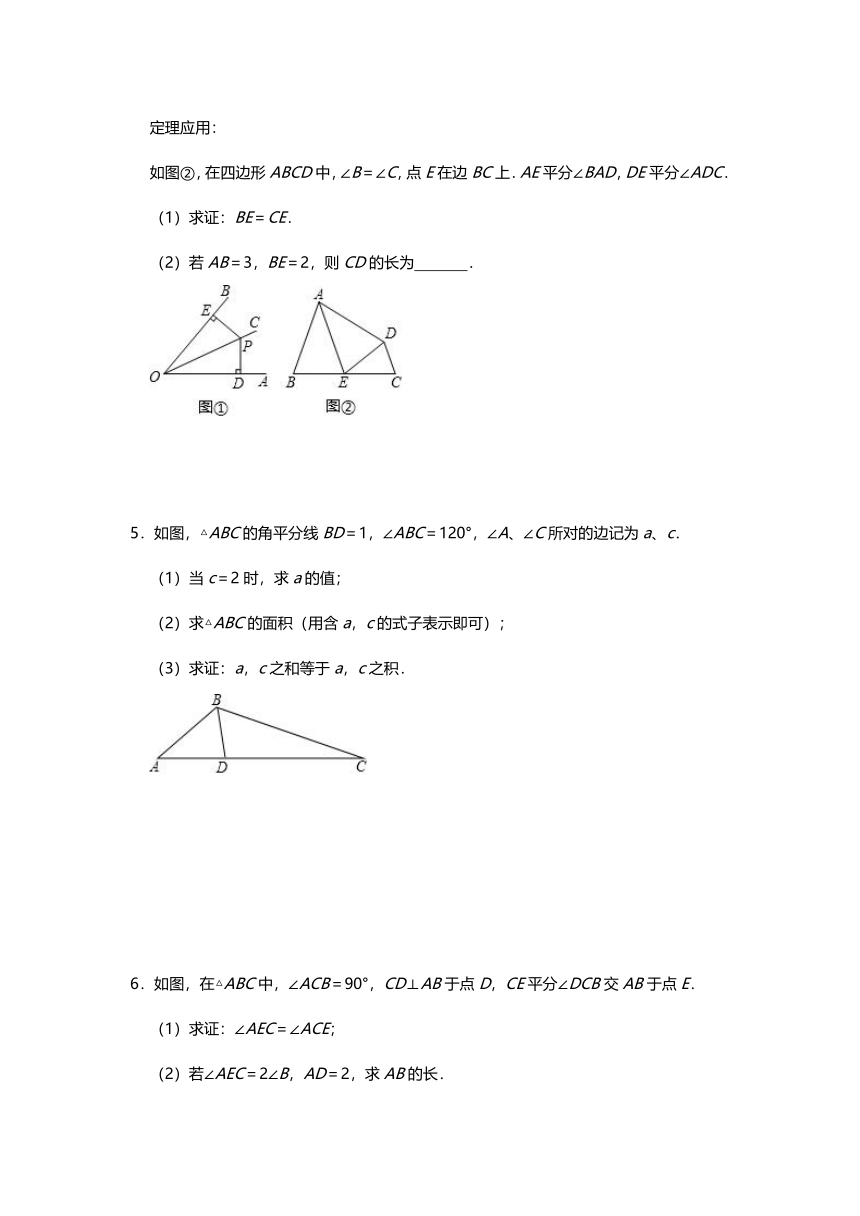
定理应用:
如图②,在四边形ABCD中,∠B=∠C,点E在边BC上.AE平分∠BAD,DE平分∠ADC.
(1)求证:BE=CE.
(2)若AB=3,BE=2,则CD的长为 .
5.如图,△ABC的角平分线BD=1,∠ABC=120°,∠A、∠C所对的边记为a、c.
(1)当c=2时,求a的值;
(2)求△ABC的面积(用含a,c的式子表示即可);
(3)求证:a,c之和等于a,c之积.
6.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
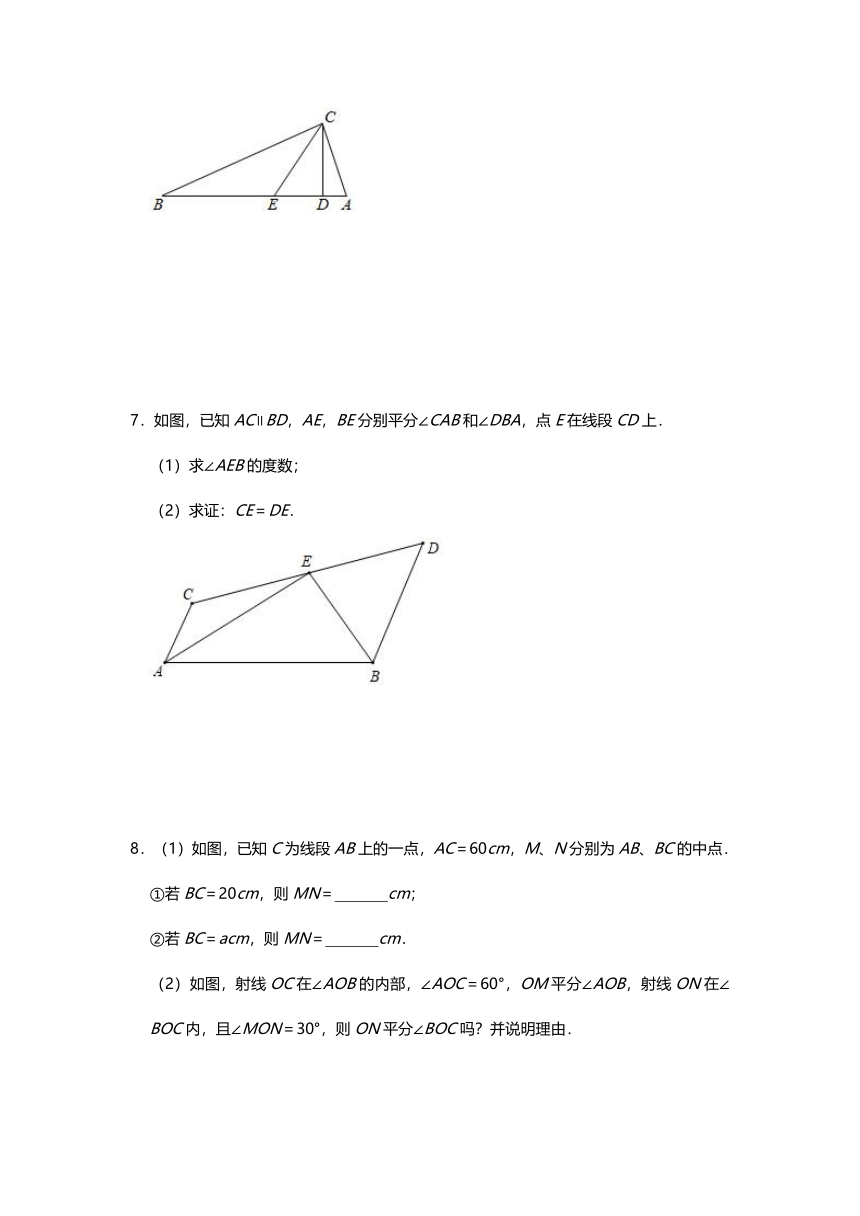
7.如图,已知AC∥BD,AE,BE分别平分∠CAB和∠DBA,点E在线段CD上.
(1)求∠AEB的度数;
(2)求证:CE=DE.
8.(1)如图,已知C为线段AB上的一点,AC=60cm,M、N分别为AB、BC的中点.
①若BC=20cm,则MN= cm;
②若BC=acm,则MN= cm.
(2)如图,射线OC在∠AOB的内部,∠AOC=60°,OM平分∠AOB,射线ON在∠BOC内,且∠MON=30°,则ON平分∠BOC吗?并说明理由.
9.如图,点B,C分别在∠A的两边上,点D是∠A内一点,DE⊥AB,DF⊥AC,垂足分别为E,F,且AB=AC,DE=DF.求证:BD=CD.
10.已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
11.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
12.如图,D是∠EAF平分线上的一点,若∠ACD+∠ABD=180°,请说明CD=DB的理由.
13.已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.求证:点O到EB与ED的距离相等.
14.在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
15.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
参考答案
1.证明:(1)∵∠C=60°,AD、BE是△ABC的角平分线,
∴∠ABP=∠ABC,∠BAP=∠BAC,
∴∠BAP+∠MBP=(∠ABC+∠BAC)=(180°﹣∠C)=60°,
∴∠APB=120°;
(2)如图1,过P作PF⊥AB,PG⊥AC,PH⊥BC,
∵AD,BE分别平分∠CAB,∠CBA,
∴PF=PG,PF=PH,
∴PH=PG,
∴点P在∠C的平分线上;
(3)如图2,在AB上取点M使AM=AE,连接PM
∵AD是∠BAC的平分线,
∴∠PAM=∠PAE,
在△AMP与△AEP中,,
∴△AMP≌△AEP,
∴∠APM=∠APE=180°﹣∠APB=60°,
∴∠BPM=180°﹣(∠APM+∠APE)=60°,∠BPD=∠APE=60°,
∴∠BPM=∠BPD,
∵BE是∠ABC的角平分线,
∴∠MBP=∠DBP,
在△BPM与△BPD中,,
∴△BPM≌△BPD,
∴BM=BD,
∴AB=AM+BM=AE+BD.
2.解:(1)在图1中,作DE⊥AB,DF⊥AC,
∵AD平分∠BAC,
∴DE=DF,
∵S△ABD=AB×DE,S△ACD=AC×DF,
∴S△ABD:S△ACD=AB:AC.
故答案案为:DE=DF,AB、DE,AC、DF,AB:AC;
(2)在图2中,作AP⊥BC,
∵BD×AP,CD×AP,
∴S△ABD:S△ACD=BD:CD;
故答案为:BD、AP,CD、AP,BD、CD;
(3)∵(1)中,S△ABD:S△ACD=AB:AC,
在(2)中,S△ABD:S△ACD=BD:CD,
∴AB:AC=BD:CD.
故答案为:AB、AC、BD、CD.
3.证明:连接FE,
∵CD是Rt△ABC斜边上的高,
∴∠A=∠DCB,
又∵AE平分∠A,CF平分∠BCD,
∴∠DCF=∠DAE,
又∵∠AHD=∠CHE,∠ADH=90°,
∴∠CGH=90°,
∴∠GAC+∠ACG=90°,∠GAF+∠AFG=90°,
∵∠GAC=∠GAF,
∴∠ACG=∠AFG,
∴AC=AF,
∴CG=FG,
同法可证,CH=CE,
∴CH=HF=EF=CE,
∴四边形HCEF是菱形,
∴HF∥BC.
4.解:已知:射线OC是∠AOB的角平分线,PE⊥OB于E,PD⊥OA于D,
求证:PE=PD,
证明:∵OC是∠AOB的角平分线,
∴∠AOP=∠BOP,
∵PE⊥OB于EPD⊥OA于D,
∴∠PEO=∠PDO=90°,
在△POD与△POE中,,
∴△POD≌△POE(AAS),
∴PD=PE;
(1)过E作EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,
∵AE平分∠BAD,DE平分∠ADC,
∴EF=EG=EH,
在△BEF与△CEH中,
∴△BEF≌△CEH(AAS),
∴BE=CE;
(2)∵∠HEC=∠BEF,∠HED=∠DEG,∠GEA=∠AEF
又∵∠HEC+∠BEF+∠HED+∠DEG+∠GEA+∠AEF=180°
∴∠BEF+∠HED+∠AEF=90°
又∵∠EDH+∠DEH=90°,
∴∠EDH=∠AEB,
∵∠B=∠C,
∴△ABE∽△ECD
∴,
即:AB?CD=BE?EC
∴3CD=2×2,
CD=
故答案为:
5.解:(1)∵BD平分∠ABC,∠ABC=120°,
∴∠ABD=∠CBD=60°,
过D作DE⊥AB于E,过D作DF⊥BC于F,
∴DE=DF,
∵BD=1,
∴BE=BF=,DE=DF=,
过A作AG⊥BC于G,
∴AG=AB=,
∵S△ABC=BC?AG=×a=×2×+a,
∴a=2;
(2)△ABC的面积=BC?AG=×c×a=ac;
(3)∵S△BAC=S△ABD+S△BCD,
∴BC?AG=AB?DE+BC?DF,
∴?a?c=×(c+a),
∴ac=a+c,
∴a,c之和等于a,c之积.
6.解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴Rt△ACD中,AC=2AD=4,
∴Rt△ABC中,AB=2AC=8.
7.解:(1)∵AC∥BD,∴∠CAB+∠ABD=180°.
∵AE平分∠CAB,∴∠EAB=∠CAB.
同理可得∠EBA=∠ABD.
∴∠EAB+∠EBA=90°,
∴∠AEB=90°;
(2)如图,在AB上截取AF=AC,连接EF,
在△ACE和△AFE中,
∴△ACE≌△AFE(SAS).
∴CE=FE,∠CEA=∠FEA.
∵∠CEA+∠DEB=90°,∠FEA+∠FEB=90°,
∴∠DEB=∠FEB.
在△DEB和△FEB中
∴△DEB≌△FEB(ASA).
∴ED=EF.
∴ED=CE.
8.解:(1)①∵BC=20,N为BC中点,
∴BN=BC=10.
又∵M为AB中点,
∴MB=AB=40.
∴MN=MB﹣BN=40﹣10=30.
故答案为30;
②当BC=a时,AB=60+a,
BN=a,MB=AB=30+a,
∴MN=MB﹣BN=30.
故答案为30;
(2)平分
理由:∵OM分别平分∠AOB,
∴∠BOM=∠AOB
=(∠AOC+∠BOC)
=30°+∠BOC.
又∵∠BOM=∠MON+∠BON=30°+∠BON,
∴∠BON=∠BOC.
∴ON平分∠BOC.
故答案为30,30.
9.证明:连接AD,
∵DE⊥AB,DF⊥AC,DE=DF,
∴∠BAD=∠CAD,
在△ABD和△ACD中
,
∴△ABD≌△ACD,(SAS),
∴BD=CD.
10.证明:连接BF,
∵F是△ABC的角平分线交点,
∴BF也是角平分线,
∵FM⊥AB,FN⊥BC,
∴MF=FN,∠DNF=∠EMF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=∠BAC=15°,
∴∠CDA=75°,
∵∠NFC=45°,∠MFN=120°,
∴∠MFE=15°,
∴∠MEF=75°=∠NDF,
在△DNF和△EMF中,
,
∴△DNF≌△EMF(AAS),
∴FE=FD.
11.(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,
解得:x=1,
∴BE=1,AE=AB﹣BE=5﹣1=4.
12.解:过点D分别作AE,AF的垂线,交AE于M,交AF于N
则∠CMD=∠BND=90°,
∵AD是∠EAF的平分线,
∴DM=DN,
∵∠ACD+∠ABD=180°,
∠ACD+∠MCD=180°,
∴∠MCD=∠NBD,
在△CDM和△BDN中,
∠CMD=∠BND=90°,
∠MCD=∠NBD,
DM=DN,
∴△CDM≌△BDN,
∴CD=DB.
13.证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°,
∴∠DOC=∠BOC,
又∵CO=CO,∠DCO=∠BCO,
∴△DCO≌△BCO(ASA)
∴CB=CD,
∴OB=OD,
∴CE是BD的垂直平分线,
∴EB=ED,又∠DOC=90°,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.
14.解:(1)
过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1,
故答案为:1:1;
(2)
过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)
∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
15.(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在Rt△CDF与Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12﹣x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=12﹣x,
解得x=2,即CF=2.
角平分线解答题专项(三)
1.如图,△ABC中,∠C=60°,AD,BE分别平分∠CAB,∠CBA、AD、BE交于点P.求证:
(1)∠APB=120°;
(2)点P在∠C的平分线上;
(3)AB=AE+BD.
2.如图,已知△ABC中,AD平分∠BAC.
(1)在图1中,作DE⊥AB,DF⊥AC,
∵AD平分∠BAC,∴ = ,
而S△ABD= × ,
S△ACD= ×
则S△ABD:S△ACD= :
(2)在图2中,作AP⊥BC而 × , × ,
则S△ABD:S△ACD= : ;
(3)由(1)、(2)可得“角平分线”第二性质 : = : .
3.已知如图,CD是RT△ABC斜边上的高,∠A的平分线交CD于H,交∠BCD的平分线于G,求证:HF∥BC.
4.教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,在四边形ABCD中,∠B=∠C,点E在边BC上.AE平分∠BAD,DE平分∠ADC.
(1)求证:BE=CE.
(2)若AB=3,BE=2,则CD的长为 .
5.如图,△ABC的角平分线BD=1,∠ABC=120°,∠A、∠C所对的边记为a、c.
(1)当c=2时,求a的值;
(2)求△ABC的面积(用含a,c的式子表示即可);
(3)求证:a,c之和等于a,c之积.
6.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
7.如图,已知AC∥BD,AE,BE分别平分∠CAB和∠DBA,点E在线段CD上.
(1)求∠AEB的度数;
(2)求证:CE=DE.
8.(1)如图,已知C为线段AB上的一点,AC=60cm,M、N分别为AB、BC的中点.
①若BC=20cm,则MN= cm;
②若BC=acm,则MN= cm.
(2)如图,射线OC在∠AOB的内部,∠AOC=60°,OM平分∠AOB,射线ON在∠BOC内,且∠MON=30°,则ON平分∠BOC吗?并说明理由.
9.如图,点B,C分别在∠A的两边上,点D是∠A内一点,DE⊥AB,DF⊥AC,垂足分别为E,F,且AB=AC,DE=DF.求证:BD=CD.
10.已知:如图,在Rt△ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=FD.
11.如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
12.如图,D是∠EAF平分线上的一点,若∠ACD+∠ABD=180°,请说明CD=DB的理由.
13.已知:如图,AD∥BC,DB平分∠ADC,CE平分∠BCD,交AB于点E,BD于点O.求证:点O到EB与ED的距离相等.
14.在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
(1)如图1,当点D是BC边上的中点时,S△ABD:S△ACD= ;
(2)如图2,当AD是∠BAC的平分线时,若AB=m,AC=n,求S△ABD:S△ACD的值(用含m,n的代数式表示);
(3)如图3,AD平分∠BAC,延长AD到E,使得AD=DE,连接BE,如果AC=2,AB=4,S△BDE=6,那么S△ABC= .
15.如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长.
参考答案
1.证明:(1)∵∠C=60°,AD、BE是△ABC的角平分线,
∴∠ABP=∠ABC,∠BAP=∠BAC,
∴∠BAP+∠MBP=(∠ABC+∠BAC)=(180°﹣∠C)=60°,
∴∠APB=120°;
(2)如图1,过P作PF⊥AB,PG⊥AC,PH⊥BC,
∵AD,BE分别平分∠CAB,∠CBA,
∴PF=PG,PF=PH,
∴PH=PG,
∴点P在∠C的平分线上;
(3)如图2,在AB上取点M使AM=AE,连接PM
∵AD是∠BAC的平分线,
∴∠PAM=∠PAE,
在△AMP与△AEP中,,
∴△AMP≌△AEP,
∴∠APM=∠APE=180°﹣∠APB=60°,
∴∠BPM=180°﹣(∠APM+∠APE)=60°,∠BPD=∠APE=60°,
∴∠BPM=∠BPD,
∵BE是∠ABC的角平分线,
∴∠MBP=∠DBP,
在△BPM与△BPD中,,
∴△BPM≌△BPD,
∴BM=BD,
∴AB=AM+BM=AE+BD.
2.解:(1)在图1中,作DE⊥AB,DF⊥AC,
∵AD平分∠BAC,
∴DE=DF,
∵S△ABD=AB×DE,S△ACD=AC×DF,
∴S△ABD:S△ACD=AB:AC.
故答案案为:DE=DF,AB、DE,AC、DF,AB:AC;
(2)在图2中,作AP⊥BC,
∵BD×AP,CD×AP,
∴S△ABD:S△ACD=BD:CD;
故答案为:BD、AP,CD、AP,BD、CD;
(3)∵(1)中,S△ABD:S△ACD=AB:AC,
在(2)中,S△ABD:S△ACD=BD:CD,
∴AB:AC=BD:CD.
故答案为:AB、AC、BD、CD.
3.证明:连接FE,
∵CD是Rt△ABC斜边上的高,
∴∠A=∠DCB,
又∵AE平分∠A,CF平分∠BCD,
∴∠DCF=∠DAE,
又∵∠AHD=∠CHE,∠ADH=90°,
∴∠CGH=90°,
∴∠GAC+∠ACG=90°,∠GAF+∠AFG=90°,
∵∠GAC=∠GAF,
∴∠ACG=∠AFG,
∴AC=AF,
∴CG=FG,
同法可证,CH=CE,
∴CH=HF=EF=CE,
∴四边形HCEF是菱形,
∴HF∥BC.
4.解:已知:射线OC是∠AOB的角平分线,PE⊥OB于E,PD⊥OA于D,
求证:PE=PD,
证明:∵OC是∠AOB的角平分线,
∴∠AOP=∠BOP,
∵PE⊥OB于EPD⊥OA于D,
∴∠PEO=∠PDO=90°,
在△POD与△POE中,,
∴△POD≌△POE(AAS),
∴PD=PE;
(1)过E作EF⊥AB于F,EG⊥AD于G,EH⊥CD于H,
∵AE平分∠BAD,DE平分∠ADC,
∴EF=EG=EH,
在△BEF与△CEH中,
∴△BEF≌△CEH(AAS),
∴BE=CE;
(2)∵∠HEC=∠BEF,∠HED=∠DEG,∠GEA=∠AEF
又∵∠HEC+∠BEF+∠HED+∠DEG+∠GEA+∠AEF=180°
∴∠BEF+∠HED+∠AEF=90°
又∵∠EDH+∠DEH=90°,
∴∠EDH=∠AEB,
∵∠B=∠C,
∴△ABE∽△ECD
∴,
即:AB?CD=BE?EC
∴3CD=2×2,
CD=
故答案为:
5.解:(1)∵BD平分∠ABC,∠ABC=120°,
∴∠ABD=∠CBD=60°,
过D作DE⊥AB于E,过D作DF⊥BC于F,
∴DE=DF,
∵BD=1,
∴BE=BF=,DE=DF=,
过A作AG⊥BC于G,
∴AG=AB=,
∵S△ABC=BC?AG=×a=×2×+a,
∴a=2;
(2)△ABC的面积=BC?AG=×c×a=ac;
(3)∵S△BAC=S△ABD+S△BCD,
∴BC?AG=AB?DE+BC?DF,
∴?a?c=×(c+a),
∴ac=a+c,
∴a,c之和等于a,c之积.
6.解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴Rt△ACD中,AC=2AD=4,
∴Rt△ABC中,AB=2AC=8.
7.解:(1)∵AC∥BD,∴∠CAB+∠ABD=180°.
∵AE平分∠CAB,∴∠EAB=∠CAB.
同理可得∠EBA=∠ABD.
∴∠EAB+∠EBA=90°,
∴∠AEB=90°;
(2)如图,在AB上截取AF=AC,连接EF,
在△ACE和△AFE中,
∴△ACE≌△AFE(SAS).
∴CE=FE,∠CEA=∠FEA.
∵∠CEA+∠DEB=90°,∠FEA+∠FEB=90°,
∴∠DEB=∠FEB.
在△DEB和△FEB中
∴△DEB≌△FEB(ASA).
∴ED=EF.
∴ED=CE.
8.解:(1)①∵BC=20,N为BC中点,
∴BN=BC=10.
又∵M为AB中点,
∴MB=AB=40.
∴MN=MB﹣BN=40﹣10=30.
故答案为30;
②当BC=a时,AB=60+a,
BN=a,MB=AB=30+a,
∴MN=MB﹣BN=30.
故答案为30;
(2)平分
理由:∵OM分别平分∠AOB,
∴∠BOM=∠AOB
=(∠AOC+∠BOC)
=30°+∠BOC.
又∵∠BOM=∠MON+∠BON=30°+∠BON,
∴∠BON=∠BOC.
∴ON平分∠BOC.
故答案为30,30.
9.证明:连接AD,
∵DE⊥AB,DF⊥AC,DE=DF,
∴∠BAD=∠CAD,
在△ABD和△ACD中
,
∴△ABD≌△ACD,(SAS),
∴BD=CD.
10.证明:连接BF,
∵F是△ABC的角平分线交点,
∴BF也是角平分线,
∵FM⊥AB,FN⊥BC,
∴MF=FN,∠DNF=∠EMF=90°,
∵在Rt△ABC中,∠ACB=90°,∠ABC=60°,
∴∠BAC=30°,
∴∠DAC=∠BAC=15°,
∴∠CDA=75°,
∵∠NFC=45°,∠MFN=120°,
∴∠MFE=15°,
∴∠MEF=75°=∠NDF,
在△DNF和△EMF中,
,
∴△DNF≌△EMF(AAS),
∴FE=FD.
11.(1)证明:连接BD,CD,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,
解得:x=1,
∴BE=1,AE=AB﹣BE=5﹣1=4.
12.解:过点D分别作AE,AF的垂线,交AE于M,交AF于N
则∠CMD=∠BND=90°,
∵AD是∠EAF的平分线,
∴DM=DN,
∵∠ACD+∠ABD=180°,
∠ACD+∠MCD=180°,
∴∠MCD=∠NBD,
在△CDM和△BDN中,
∠CMD=∠BND=90°,
∠MCD=∠NBD,
DM=DN,
∴△CDM≌△BDN,
∴CD=DB.
13.证明:∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DB平分∠ADC,CE平分∠BCD,
∴∠ODC+∠OCD=90°,
∴∠DOC=90°,
∴∠DOC=∠BOC,
又∵CO=CO,∠DCO=∠BCO,
∴△DCO≌△BCO(ASA)
∴CB=CD,
∴OB=OD,
∴CE是BD的垂直平分线,
∴EB=ED,又∠DOC=90°,
∴EC平分∠BED,
∴点O到EB与ED的距离相等.
14.解:(1)
过A作AE⊥BC于E,
∵点D是BC边上的中点,
∴BD=DC,
∴SABD:S△ACD=(×BD×AE):(×CD×AE)=1:1,
故答案为:1:1;
(2)
过D作DE⊥AB于E,DF⊥AC于F,
∵AD为∠BAC的角平分线,
∴DE=DF,
∵AB=m,AC=n,
∴SABD:S△ACD=(×AB×DE):(×AC×DF)=m:n;
(3)
∵AD=DE,
∴由(1)知:S△ABD:S△EBD=1:1,
∵S△BDE=6,
∴S△ABD=6,
∵AC=2,AB=4,AD平分∠CAB,
∴由(2)知:S△ABD:S△ACD=AB:AC=4:2=2:1,
∴S△ACD=3,
∴S△ABC=3+6=9,
故答案为:9.
15.(1)证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在Rt△CDF与Rt△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
(2)解:设CF=x,则AE=12﹣x,
∵AD平分∠BAC,DE⊥AB,
∴CD=DE.
在Rt△ACD与Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,即8+x=12﹣x,
解得x=2,即CF=2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
