2020-2021学年 冀教版七年级数学下册 第6章 二元一次方程组 单元综合培优训练(Word版含答案)
文档属性
| 名称 | 2020-2021学年 冀教版七年级数学下册 第6章 二元一次方程组 单元综合培优训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 141.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览




文档简介
2021年度冀教版七年级数学下册《第6章 二元一次方程组》单元综合培优训练(附答案)
1.一个两位数加18所得的数是它的个位数字与十位数字换了位置后的数,则这个两位数是( )
A.13 B.13或14 C.有9种可能 D.有7种可能
2.若|3x+2y﹣4|与6(5x+7y﹣3)2互为相反数,则x与y的值是( )
A. B. C.不存在 D.无法求出
3.某汽车制造厂接受了在预定期限内生产一批汽车的任务,如果每天生产35辆,则差10辆才能完成任务;如果每天生产40辆,则可超额生产20辆,试求预定期限是多少天?计划生产多少辆汽车?( )
A.预定期限为6天,需要制造的汽车总数是200辆
B.预定期限为6天,需要制造的汽车总数是220辆
C.预定期限为7天,需要制造的汽车总数是220辆
D.预定期限为7天,需要制造的汽车总数是200辆
4.若关于x,y的方程组没有实数解,则( )
A.ab=﹣2 B.ab=﹣2且a≠1 C.ab≠﹣2 D.ab=﹣2且a≠2
5.一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付给两组费用共3480元,若装修完后,商店每天可盈利200元,你认为如何安排施工有利用商店经营?( )
A.甲单独 B.乙单独
C.甲、乙同时做 D.以上都不对
6.已知实数x、y、z满足3x+7y+z=5,4x+10y+z=3,则x+y+z=( )
A.9 B.10 C.12 D.不确定
7.某工厂现向银行申请了两种贷款,共计35万元,每年需付利息2.25万元,甲种贷款每年的利率是7%,乙种贷款每年的利率是6%,求这两种贷款的数额各是多少.若设甲、乙两种贷款的数额分别为x万元和y万元,则( )
A.x=15,y=20 B.x=12,y=23 C.x=20,y=15 D.x=23,y=12
8.如图,在长方形ABCD中,放入六个形状、大小相同的小长方形(即空白的长方形),若AB=16cm,EF=4cm,则一个小长方形的面积为( )
A.16cm2 B.21cm2 C.24cm2 D.32 cm2
9.若x=时,关于x,y的二元一次方程组的解x,y互为倒数,则a﹣2b= .
10.小龙和小刚两人玩“打弹珠”游戏,小龙对小刚说:“把你珠子的一半给我,我就有10颗珠子”.小刚却说:“只要把你珠子的给我,我就有10颗”,那么小刚的弹珠颗数是 颗.
11.若的解是方程ax﹣3y=2的一组解,则a的值是 .
12.若关于x、y的方程组的解满足x+y=1,则k= .
13.若x、y满足方程组,则x+y= .
14.已知关于x,y的二元一次方程组的解互为相反数,则k的值是 .
15.解方程组,小明正确解得,小丽只看错了c解得,则当x=﹣1时,代数式ax2﹣bx+c的值为 .
16.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中方程术是重要的数学成就.书中有一个方程问题:“五只雀,六只燕,共重1斤(等于16两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少?”设每只雀有x两,每只燕有y两,则可列方程组为 .
17.欣欣超市为促销,决定对A,B两种商品统一进行打8折销售,打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元,打折后,小敏买50件A商品和40件B商品仅需 元.
18.如图,长方形ABCD的边AB比BC大2,且恰好被分成6个正方形,则这个长方形的周长是 .
19.如图,7个大小、形状完全相同的小长方形组成1个周长为68的大长方形,则大长方形的面积为 .
20.矩形ABCD中放置了6个形状、大小都相同的小矩形,所标尺寸如图所示,则图中阴影部分的面积是 cm2.
21.在疫情防控期间,某中学为保障广大师生生命健康安全,预从商场购进一批免洗手消毒液和84消毒液.如果购买40瓶免洗手消毒液和90瓶84消毒液,共需花费1320元,如果购买60瓶免洗手消毒液和120瓶84消毒液,共需花费1860元.
(1)每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?
(2)若商场有两种促销方案:方案一,所有购买商品均打九折;方案二,购买5瓶免洗手消毒液送2瓶84消毒液,学校打算购进免洗手消毒液100瓶,84消毒液60瓶,请问学校选用哪种方案更节约钱?节约多少钱?
22.在手工制作课上,老师组织班级同学用硬纸制作圆柱形茶叶筒.全班共有学生50人,其中男生x人,女生y人,男生人数比女生人数少2人.已知每名同学每小时剪筒身40个或剪筒底120个.
(1)求这个班男生、女生各有多少人?
(2)原计划男生负责剪筒底,女生负责剪筒身,若要求一个筒身配两个筒底,请说明每小时剪出的筒身与筒底能否配套?如果不配套,请说明如何调配人员,才能使每小时剪出的筒身与筒底刚好配套?
23.在期末一节复习课上,八年(一)班的数学老师要求同学们列二元一次方程组解下列问题:
在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建3000m的村路,甲队每天修建150m,乙队每天修建200m,共用18天完成.
(1)粗心的张红同学,根据题意,列出的两个二元一次方程,等号后面忘记写数据,得到了一个不完整的二元一次方程组,张红列出的这个不完整的方程组中未知数p表示的是 ,未知数q表示的是 ;张红所列出正确的方程组应该是 ;
(2)李芳同学的思路是想设甲工程队修建了xm村路,乙工程队修建了ym村路.下面请你按照李芳的思路,求甲、乙两个工程队分别修建了多少天?
24.解下列方程组:
(1) (2)
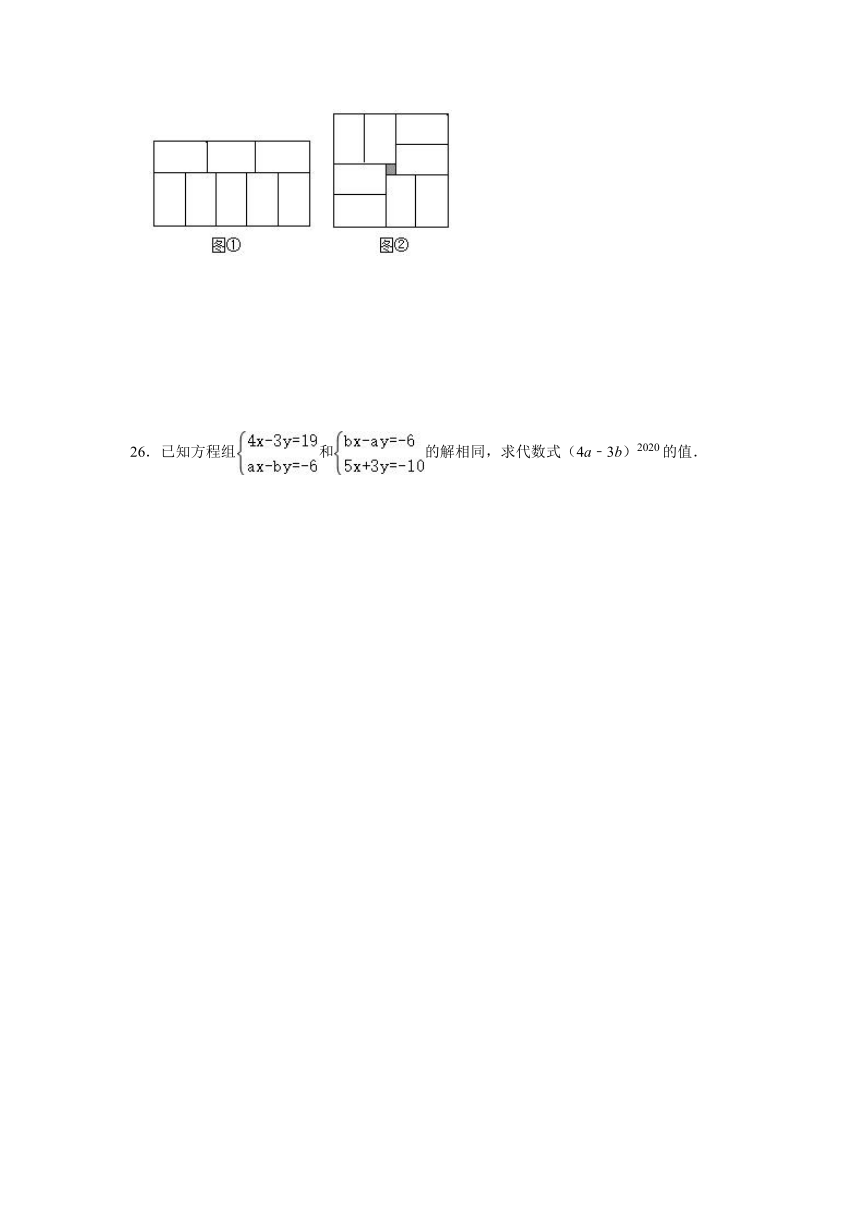
25.分别用8个大小一样的长方形拼图.如图①,小明拼成了一个大的长方形;如图②,小红拼成了一个大的正方形,但中间恰好空出一个边长为1mm的小正方形.你能求出小长方形的长和宽吗?
26.已知方程组和的解相同,求代数式(4a﹣3b)2020的值.
参考答案
1.解:设原两位数的十位数字为a,个位数字为b,
则10a+b+18=10b+a,
∴b﹣a=2,
∴b=a+2.
a可取1,2,3,4,5,6,7,
故有7种可能.
故选:D.
2.解:依题意得:
|3x+2y﹣4|+6(5x+7y﹣3)2=0,
∴,
①×5﹣②×3得:﹣11y﹣11=0,∴y=﹣1.
①×7﹣②×2得:11x﹣22=0,∴x=2.
故选:B.
3.解:设预定期限为x天,需要制造的汽车总数为y辆,
根据题意,得.
解得,
答:预定期限为6天,需要制造的汽车总数是220辆.
故选:B.
4.解:,
由①得,x=﹣1﹣ay,
代入②得,b(﹣1﹣ay)﹣2y+a=0,
即(﹣ab﹣2)y=b﹣a,
因为此方程组没有实数根,所以﹣ab﹣2=0,ab=﹣2.
故选:A.
5.解:设甲组单独做需要x天,乙单独做需要y天,
由题意得,,
解得:,
设甲单独做每天需要a元,乙单独做每天需要b元,
由题意得,,
解得:,
则甲组单独做12天完成,需付款3600元,乙组单独做24天完成,需付款3360元,由于甲组装修完比乙组装修完商店早开张12天,12天可以盈利200×12=2400元,即选择甲组装修相当只付装修费用1200元,所以选择甲单独做比选择乙单独做合算.
甲、乙同时做需8天完成,需付款3520元又比甲组单独做少用4天,4天可以盈利200×4=800元,3520﹣800=2720元,这个数字又比甲单独做12天用3600元和算.
综上所述,选择甲、乙两组合做8天的方案最佳.
故选:C.
6.解:由x、y、z满足3x+7y+z=5和4x+10y+z=3,
得出:,
解得:,
故选:A.
7.解:依题意,得,
解,得.
故选:A.
8.解:设小长方形的长为x,宽为y,如图可知,
,
解得:.
所以小长方形的面积=3×7=21(cm2).
故选:B.
9.解:由于x、y互为倒数,x=,则y=2,
代入二元一次方程组,
得,
解得a=10,b=﹣,
则a﹣2b=11.
故本题答案为:11.
10.解:设小刚的弹珠数是x个,小龙的是y个.
则,
解得,
那么小刚的弹珠颗数是8.
11.解:解方程组得:,
把代入方程ax﹣3y=2得:﹣a﹣6=2,
解得:a=﹣8,
故答案为:﹣8.
12.解:,
①+②得:5(x+y)=3k,即x+y=k,
代入x+y=1中得:k=,
故答案为:
13.解:
由②,可得:y=4﹣2x③,
把③代入①,解得x=1,
∴y=4﹣2×1=2,
∴原方程组的解是,
∴x+y=1+2=3
故答案为:3.
14.解:,
①+②得:3(x+y)=k﹣1,
解得:x+y=,
由题意得:x+y=0,
可得=0,
解得:k=1,
故答案为:1
15.解:把代入方程组得:,
解②得:c=5,
把代入ax+by=6得:﹣2a+b=6③,
由①和③组成方程组,
解得:a=﹣1.5,b=3,
当x=﹣1时,ax2﹣bx+c=﹣1.5×(﹣1)2﹣3×(﹣1)+5=6.5,
故答案为:6.5.
16.解:设每只雀有x两,每只燕有y两,
由题意得,.
故答案为.
17.解:设A、B两种商品的售价分别是1件x元和1件y元,
根据题意得,
解得.
所以0.8(8×50+2×40)=384(元).
即打折后,小敏买50件A商品和40件B商品仅需384元.
故答案为384.
18.解:设正方形的边长分别为a、b、c、d、e,如图所示.
观察图形可知:d=2a﹣e,b=a+e,c=b+e=a+2e=d﹣e=2a﹣2e.
根据题意得:,
解得:,
∴C长方形ABCD=2(2a+b+a+d)=12a=48.
故答案为:48.
19.解:设小长方形的长为x,宽为y,
,
解得,,
∴大长方形的长为:2x=20,宽为:x+y=14,
∴大长方形的面积是:20×14=280,
故答案为:280.
20.解:设小长方形的长、宽分别为xcm,ycm,
依题意得,
解得:,
∴小长方形的长、宽分别为7cm,2cm,
∴S阴影部分=S四边形ABCD﹣6×S小长方形=13×9﹣6×2×7=33cm2.
故答案为:33.
21.解:(1)设每瓶免洗手消毒液和每瓶84消毒液的价格分别是a元、b元,
,
解得,
即每瓶免洗手消毒液和每瓶84消毒液的价格分别是15元、8元;
(2)方案一的花费为:(15×100+8×60)×0.9=1782(元),
方案二的化为为:15×100+8×(60﹣100÷5×2)=1660(元),
1782﹣1660=122(元),1782>1660,
答:学校选用方案二更节约钱,节约122元.
22.解:(1)由题意得:,
解得:,
答:这个班有男生有24人,女生有26人;
(2)男生剪筒底的数量:24×120=2880(个),
女生剪筒身的数量:26×40=1040(个),
因为一个筒身配两个筒底,2880:1040≠2:1,
所以原计划男生负责剪筒底,女生负责剪筒身,每小时剪出的筒身与筒底不能配套,
设男生应向女生支援a人,
由题意得:120(24﹣a)=(26+a)×40×2,
解得:a=4,
答:原计划男生负责剪筒底,女生负责剪筒身,每小时剪出的筒身与筒底不能配套;男生应向女生支援4人时,才能使每小时剪出的筒身与筒底配套.
23.解:(1)方程组中未知数p表示的是:甲工程队修建的天数,
未知数q表示的是:乙工程队修建的天数,
列出正确的方程组应该是:
.
故答案为:甲工程队修建的天数,乙工程队修建的天数,;
(2)设甲工程队修建了xm村路,乙工程队修建了ym村路,
根据题意,得,
解得,
所以甲工程队修建的天数:1800÷150=12(天),
乙工程队修建的天数:1200÷200=6(天).
答:甲、乙两个工程队分别修建了12天、6天.
24.解:(1),
由②得:x=y+4③代入①得3(y+4)+4y=19,
解得:y=1,
把y=1代入③得x=5,
则方程组的解为;
(2)方程组整理得:,
①+②×4得:﹣37y=74,
解得:y=﹣2,
把y=﹣2代入①得:x=﹣,
则方程组的解为.
25.解:设小长方形的长为xmm,宽为ymm,
根据题意得:,
解得:.
答:小长方形的长为5mm,宽为3mm.
26.解:联立得:,
①+②得:9x=9,
解得:x=1,
把x=1代入①得:y=﹣5,
把代入得:,
解得:a=b=﹣1,
则原式=1.
1.一个两位数加18所得的数是它的个位数字与十位数字换了位置后的数,则这个两位数是( )
A.13 B.13或14 C.有9种可能 D.有7种可能
2.若|3x+2y﹣4|与6(5x+7y﹣3)2互为相反数,则x与y的值是( )
A. B. C.不存在 D.无法求出
3.某汽车制造厂接受了在预定期限内生产一批汽车的任务,如果每天生产35辆,则差10辆才能完成任务;如果每天生产40辆,则可超额生产20辆,试求预定期限是多少天?计划生产多少辆汽车?( )
A.预定期限为6天,需要制造的汽车总数是200辆
B.预定期限为6天,需要制造的汽车总数是220辆
C.预定期限为7天,需要制造的汽车总数是220辆
D.预定期限为7天,需要制造的汽车总数是200辆
4.若关于x,y的方程组没有实数解,则( )
A.ab=﹣2 B.ab=﹣2且a≠1 C.ab≠﹣2 D.ab=﹣2且a≠2
5.一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付给两组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天可以完成,需付给两组费用共3480元,若装修完后,商店每天可盈利200元,你认为如何安排施工有利用商店经营?( )
A.甲单独 B.乙单独
C.甲、乙同时做 D.以上都不对
6.已知实数x、y、z满足3x+7y+z=5,4x+10y+z=3,则x+y+z=( )
A.9 B.10 C.12 D.不确定
7.某工厂现向银行申请了两种贷款,共计35万元,每年需付利息2.25万元,甲种贷款每年的利率是7%,乙种贷款每年的利率是6%,求这两种贷款的数额各是多少.若设甲、乙两种贷款的数额分别为x万元和y万元,则( )
A.x=15,y=20 B.x=12,y=23 C.x=20,y=15 D.x=23,y=12
8.如图,在长方形ABCD中,放入六个形状、大小相同的小长方形(即空白的长方形),若AB=16cm,EF=4cm,则一个小长方形的面积为( )
A.16cm2 B.21cm2 C.24cm2 D.32 cm2
9.若x=时,关于x,y的二元一次方程组的解x,y互为倒数,则a﹣2b= .
10.小龙和小刚两人玩“打弹珠”游戏,小龙对小刚说:“把你珠子的一半给我,我就有10颗珠子”.小刚却说:“只要把你珠子的给我,我就有10颗”,那么小刚的弹珠颗数是 颗.
11.若的解是方程ax﹣3y=2的一组解,则a的值是 .
12.若关于x、y的方程组的解满足x+y=1,则k= .
13.若x、y满足方程组,则x+y= .
14.已知关于x,y的二元一次方程组的解互为相反数,则k的值是 .
15.解方程组,小明正确解得,小丽只看错了c解得,则当x=﹣1时,代数式ax2﹣bx+c的值为 .
16.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中方程术是重要的数学成就.书中有一个方程问题:“五只雀,六只燕,共重1斤(等于16两),雀重燕轻,互换其中一只,恰好一样重,问:每只雀、燕的重量各为多少?”设每只雀有x两,每只燕有y两,则可列方程组为 .
17.欣欣超市为促销,决定对A,B两种商品统一进行打8折销售,打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元,打折后,小敏买50件A商品和40件B商品仅需 元.
18.如图,长方形ABCD的边AB比BC大2,且恰好被分成6个正方形,则这个长方形的周长是 .
19.如图,7个大小、形状完全相同的小长方形组成1个周长为68的大长方形,则大长方形的面积为 .
20.矩形ABCD中放置了6个形状、大小都相同的小矩形,所标尺寸如图所示,则图中阴影部分的面积是 cm2.
21.在疫情防控期间,某中学为保障广大师生生命健康安全,预从商场购进一批免洗手消毒液和84消毒液.如果购买40瓶免洗手消毒液和90瓶84消毒液,共需花费1320元,如果购买60瓶免洗手消毒液和120瓶84消毒液,共需花费1860元.
(1)每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?
(2)若商场有两种促销方案:方案一,所有购买商品均打九折;方案二,购买5瓶免洗手消毒液送2瓶84消毒液,学校打算购进免洗手消毒液100瓶,84消毒液60瓶,请问学校选用哪种方案更节约钱?节约多少钱?
22.在手工制作课上,老师组织班级同学用硬纸制作圆柱形茶叶筒.全班共有学生50人,其中男生x人,女生y人,男生人数比女生人数少2人.已知每名同学每小时剪筒身40个或剪筒底120个.
(1)求这个班男生、女生各有多少人?
(2)原计划男生负责剪筒底,女生负责剪筒身,若要求一个筒身配两个筒底,请说明每小时剪出的筒身与筒底能否配套?如果不配套,请说明如何调配人员,才能使每小时剪出的筒身与筒底刚好配套?
23.在期末一节复习课上,八年(一)班的数学老师要求同学们列二元一次方程组解下列问题:
在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建3000m的村路,甲队每天修建150m,乙队每天修建200m,共用18天完成.
(1)粗心的张红同学,根据题意,列出的两个二元一次方程,等号后面忘记写数据,得到了一个不完整的二元一次方程组,张红列出的这个不完整的方程组中未知数p表示的是 ,未知数q表示的是 ;张红所列出正确的方程组应该是 ;
(2)李芳同学的思路是想设甲工程队修建了xm村路,乙工程队修建了ym村路.下面请你按照李芳的思路,求甲、乙两个工程队分别修建了多少天?
24.解下列方程组:
(1) (2)
25.分别用8个大小一样的长方形拼图.如图①,小明拼成了一个大的长方形;如图②,小红拼成了一个大的正方形,但中间恰好空出一个边长为1mm的小正方形.你能求出小长方形的长和宽吗?
26.已知方程组和的解相同,求代数式(4a﹣3b)2020的值.
参考答案
1.解:设原两位数的十位数字为a,个位数字为b,
则10a+b+18=10b+a,
∴b﹣a=2,
∴b=a+2.
a可取1,2,3,4,5,6,7,
故有7种可能.
故选:D.
2.解:依题意得:
|3x+2y﹣4|+6(5x+7y﹣3)2=0,
∴,
①×5﹣②×3得:﹣11y﹣11=0,∴y=﹣1.
①×7﹣②×2得:11x﹣22=0,∴x=2.
故选:B.
3.解:设预定期限为x天,需要制造的汽车总数为y辆,
根据题意,得.
解得,
答:预定期限为6天,需要制造的汽车总数是220辆.
故选:B.
4.解:,
由①得,x=﹣1﹣ay,
代入②得,b(﹣1﹣ay)﹣2y+a=0,
即(﹣ab﹣2)y=b﹣a,
因为此方程组没有实数根,所以﹣ab﹣2=0,ab=﹣2.
故选:A.
5.解:设甲组单独做需要x天,乙单独做需要y天,
由题意得,,
解得:,
设甲单独做每天需要a元,乙单独做每天需要b元,
由题意得,,
解得:,
则甲组单独做12天完成,需付款3600元,乙组单独做24天完成,需付款3360元,由于甲组装修完比乙组装修完商店早开张12天,12天可以盈利200×12=2400元,即选择甲组装修相当只付装修费用1200元,所以选择甲单独做比选择乙单独做合算.
甲、乙同时做需8天完成,需付款3520元又比甲组单独做少用4天,4天可以盈利200×4=800元,3520﹣800=2720元,这个数字又比甲单独做12天用3600元和算.
综上所述,选择甲、乙两组合做8天的方案最佳.
故选:C.
6.解:由x、y、z满足3x+7y+z=5和4x+10y+z=3,
得出:,
解得:,
故选:A.
7.解:依题意,得,
解,得.
故选:A.
8.解:设小长方形的长为x,宽为y,如图可知,
,
解得:.
所以小长方形的面积=3×7=21(cm2).
故选:B.
9.解:由于x、y互为倒数,x=,则y=2,
代入二元一次方程组,
得,
解得a=10,b=﹣,
则a﹣2b=11.
故本题答案为:11.
10.解:设小刚的弹珠数是x个,小龙的是y个.
则,
解得,
那么小刚的弹珠颗数是8.
11.解:解方程组得:,
把代入方程ax﹣3y=2得:﹣a﹣6=2,
解得:a=﹣8,
故答案为:﹣8.
12.解:,
①+②得:5(x+y)=3k,即x+y=k,
代入x+y=1中得:k=,
故答案为:
13.解:
由②,可得:y=4﹣2x③,
把③代入①,解得x=1,
∴y=4﹣2×1=2,
∴原方程组的解是,
∴x+y=1+2=3
故答案为:3.
14.解:,
①+②得:3(x+y)=k﹣1,
解得:x+y=,
由题意得:x+y=0,
可得=0,
解得:k=1,
故答案为:1
15.解:把代入方程组得:,
解②得:c=5,
把代入ax+by=6得:﹣2a+b=6③,
由①和③组成方程组,
解得:a=﹣1.5,b=3,
当x=﹣1时,ax2﹣bx+c=﹣1.5×(﹣1)2﹣3×(﹣1)+5=6.5,
故答案为:6.5.
16.解:设每只雀有x两,每只燕有y两,
由题意得,.
故答案为.
17.解:设A、B两种商品的售价分别是1件x元和1件y元,
根据题意得,
解得.
所以0.8(8×50+2×40)=384(元).
即打折后,小敏买50件A商品和40件B商品仅需384元.
故答案为384.
18.解:设正方形的边长分别为a、b、c、d、e,如图所示.
观察图形可知:d=2a﹣e,b=a+e,c=b+e=a+2e=d﹣e=2a﹣2e.
根据题意得:,
解得:,
∴C长方形ABCD=2(2a+b+a+d)=12a=48.
故答案为:48.
19.解:设小长方形的长为x,宽为y,
,
解得,,
∴大长方形的长为:2x=20,宽为:x+y=14,
∴大长方形的面积是:20×14=280,
故答案为:280.
20.解:设小长方形的长、宽分别为xcm,ycm,
依题意得,
解得:,
∴小长方形的长、宽分别为7cm,2cm,
∴S阴影部分=S四边形ABCD﹣6×S小长方形=13×9﹣6×2×7=33cm2.
故答案为:33.
21.解:(1)设每瓶免洗手消毒液和每瓶84消毒液的价格分别是a元、b元,
,
解得,
即每瓶免洗手消毒液和每瓶84消毒液的价格分别是15元、8元;
(2)方案一的花费为:(15×100+8×60)×0.9=1782(元),
方案二的化为为:15×100+8×(60﹣100÷5×2)=1660(元),
1782﹣1660=122(元),1782>1660,
答:学校选用方案二更节约钱,节约122元.
22.解:(1)由题意得:,
解得:,
答:这个班有男生有24人,女生有26人;
(2)男生剪筒底的数量:24×120=2880(个),
女生剪筒身的数量:26×40=1040(个),
因为一个筒身配两个筒底,2880:1040≠2:1,
所以原计划男生负责剪筒底,女生负责剪筒身,每小时剪出的筒身与筒底不能配套,
设男生应向女生支援a人,
由题意得:120(24﹣a)=(26+a)×40×2,
解得:a=4,
答:原计划男生负责剪筒底,女生负责剪筒身,每小时剪出的筒身与筒底不能配套;男生应向女生支援4人时,才能使每小时剪出的筒身与筒底配套.
23.解:(1)方程组中未知数p表示的是:甲工程队修建的天数,
未知数q表示的是:乙工程队修建的天数,
列出正确的方程组应该是:
.
故答案为:甲工程队修建的天数,乙工程队修建的天数,;
(2)设甲工程队修建了xm村路,乙工程队修建了ym村路,
根据题意,得,
解得,
所以甲工程队修建的天数:1800÷150=12(天),
乙工程队修建的天数:1200÷200=6(天).
答:甲、乙两个工程队分别修建了12天、6天.
24.解:(1),
由②得:x=y+4③代入①得3(y+4)+4y=19,
解得:y=1,
把y=1代入③得x=5,
则方程组的解为;
(2)方程组整理得:,
①+②×4得:﹣37y=74,
解得:y=﹣2,
把y=﹣2代入①得:x=﹣,
则方程组的解为.
25.解:设小长方形的长为xmm,宽为ymm,
根据题意得:,
解得:.
答:小长方形的长为5mm,宽为3mm.
26.解:联立得:,
①+②得:9x=9,
解得:x=1,
把x=1代入①得:y=﹣5,
把代入得:,
解得:a=b=﹣1,
则原式=1.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
