18.1.2 平行四边形的判定(第一课时 )课件(共19张PPT)
文档属性
| 名称 | 18.1.2 平行四边形的判定(第一课时 )课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 09:13:19 | ||
图片预览


文档简介
第十八章 平行四边形
2021年春人教版八年级(下)数学
18.1.2 平行四边形的判定
第一课时
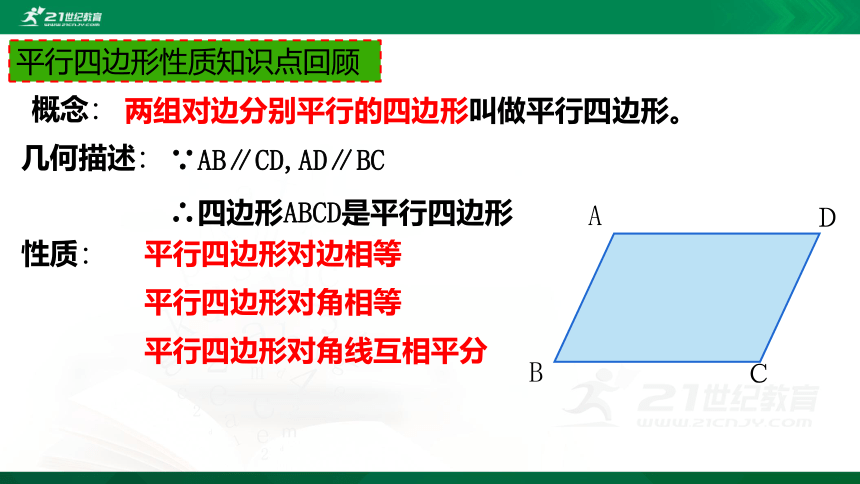
平行四边形性质知识点回顾
两组对边分别平行的四边形叫做平行四边形。
A
B
D
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
概念:
几何描述:
平行四边形对边相等
平行四边形对角相等
性质:
平行四边形对角线互相平分
1.平行四边形判定方法及应用。
2.综合运用平行四边形的判定和性质解决实际问题。
平行四边形判定方法及应用。(重点)
综合运用平行四边形的判定和性质解决实际问题。(难点)??
学习目标
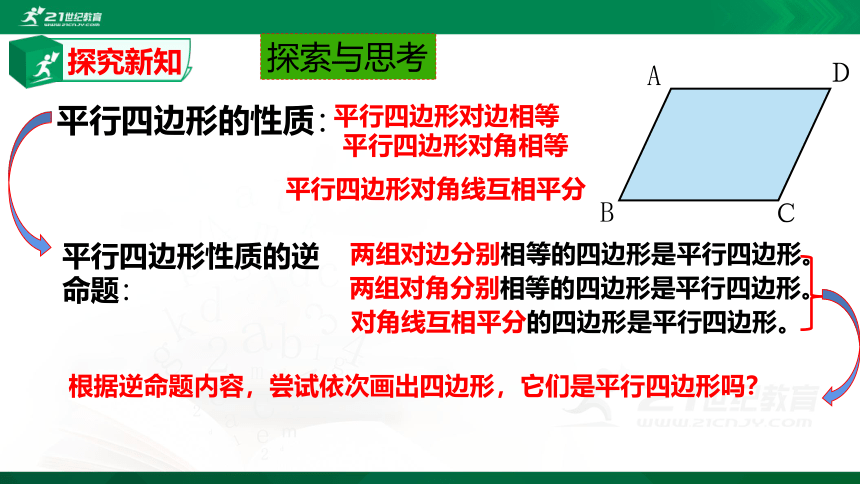
探索与思考
A
B
D
C
平行四边形的性质:
平行四边形对边相等
平行四边形对角线互相平分
根据逆命题内容,尝试依次画出四边形,它们是平行四边形吗?
平行四边形对角相等
平行四边形性质的逆命题:
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
探究新知
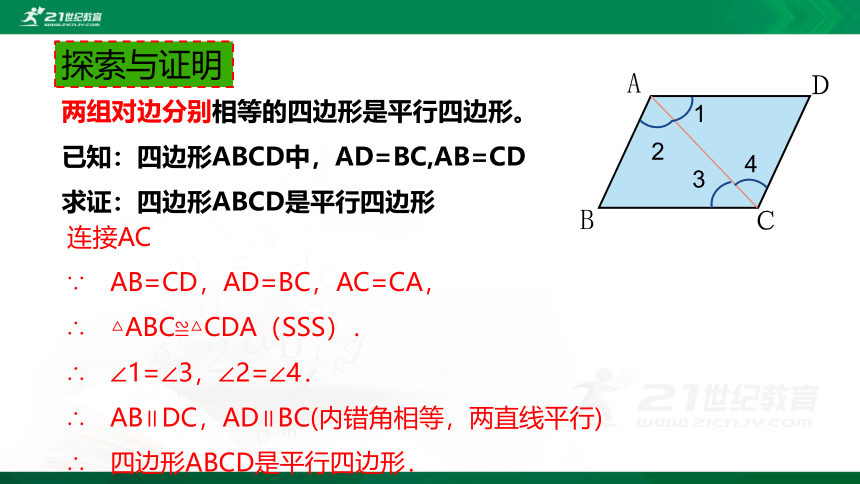
探索与证明
两组对边分别相等的四边形是平行四边形。
已知:四边形ABCD中,AD=BC,AB=CD
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
连接AC
∵ AB=CD,AD=BC,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
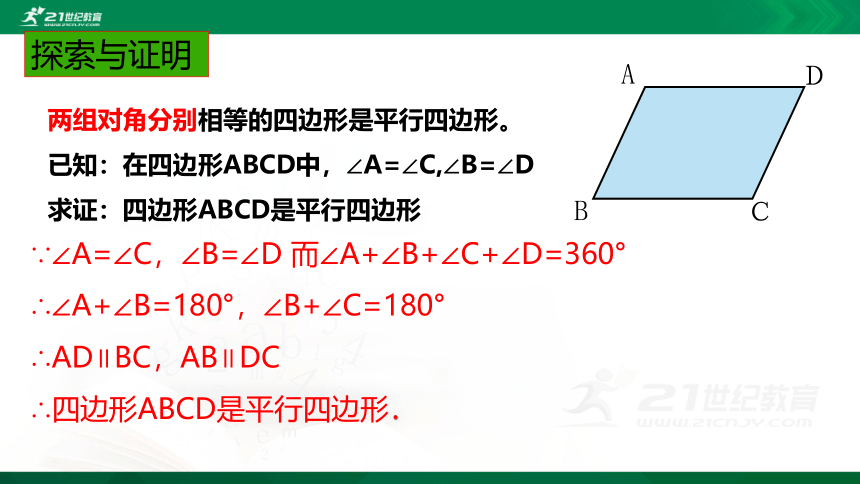
探索与证明
两组对角分别相等的四边形是平行四边形。
已知:在四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
A
B
D
C
∵∠A=∠C,∠B=∠D 而∠A+∠B+∠C+∠D=360°
∴∠A+∠B=180°,∠B+∠C=180°
∴AD∥BC,AB∥DC
∴四边形ABCD是平行四边形.
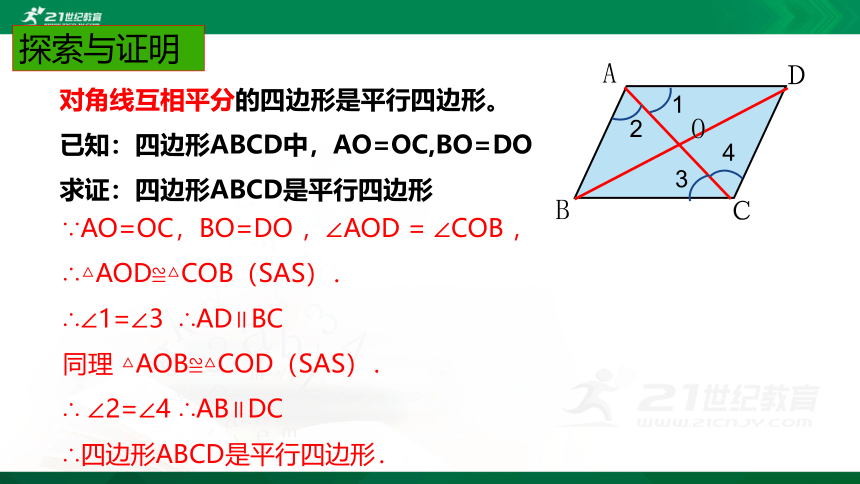
探索与证明
对角线互相平分的四边形是平行四边形。
已知:四边形ABCD中,AO=OC,BO=DO
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
O
∵AO=OC,BO=DO ,∠AOD = ∠COB ,
∴△AOD≌△COB(SAS).
∴∠1=∠3 ∴AD∥BC
同理 △AOB≌△COD(SAS).
∴ ∠2=∠4 ∴AB∥DC
∴四边形ABCD是平行四边形.
{00A15C55-8517-42AA-B614-E9B94910E393}
文字语言
图形语言
几何语言
定义法
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是平行四边形
判定方法1
两组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形
判定方法2
两组对角分别相等的四边形是平行四边形
∵∠A= ∠C, ∠B= ∠D,
∴四边形ABCD是平行四边形
判定方法3
对角线互相平分的四边形是平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
小结
1.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
【详解】
解:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.故选:A.
针对练习
2.如图,在平行四边形 ABCD中,点E、F在对角线BD上,且BE=DF.
(1)求证:AE=CF;
(2)求证:四边形AECF是平行四边形.
【详解】
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.∴∠ABE=∠CDF.
在△ABE和△CDF中,&????????=????????&∠????????????=∠????????????&????????=????????,
∴△ABE≌△DCF(SAS).
∴AE=CF.
?
(2)∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
探索与思考
若这个四边形的一组对边相等,还需添加什么条件(并尝试证明),则这个四边形是平行四边形。
已知:四边形ABCD中,AD=BC, ____?_____
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
连接AC
∵ AB=CD,AD=BC,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
条件一:AB=CD
探索与证明
若这个四边形的一组对边相等,还需添加什么条件(并尝试证明) ,则这个四边形是平行四边形。
已知:四边形ABCD中,AD=BC, ____?_____
求证:四边形ABCD是平行四边形
连接AC ∵AD∥BC ∴∠1=∠3
∵ AD=BC,∠1=∠3,AC=CA,
∴ △ABC≌△CDA(SAS).
∴ ∠2=∠4.
∴ AB∥DC 而AD∥BC
∴ 四边形ABCD是平行四边形.
条件二:AD∥BC
A
B
D
C
1
2
3
4
四边形ABCD中,AD=BC, AB∥CD,小明同学认为四边形ABCD是平行四边形?你认同吗?为什么?
小明的答案如下:
①连接AC ∵AB∥DC ∴∠2=∠4
②∵ AD=BC,AC=CA,∠2=∠4
③∴△ABC≌△CDA(SSA).
④∴∠1=∠3.
⑤∴AD∥BC而AB∥DC
⑥∴四边形ABCD是平行四边形.
A
B
D
C
1
2
3
4
探索与证明
1.如图,在?ABCD中,E、F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
证明:∵四边形ABCD是平行四边形
∴AB=CD,EB//FD
又∵EB= ?????????AB,FD= ?????????CD
∴EB=FD
∴四边形EBFD是平行四边形.
?
课堂练习
2.下列选项中,不能判定四边形ABCD是平行四边形的是( )
A.????????∥BC, ????????∥CD B. ????????∥CD , ????????=CD
C.????????∥BC, ?????????=CD D. ?????????=CD ,????????∥BC
?
【详解】
A、由????????∥BC,????????∥CD可以判断四边形ABCD是平行四边形;故本选项不符合题意;
B、由????????∥CD,????????=CD可以判断四边形ABCD是平行四边形;故本选项不符合题意;
C、????????∥BC, ?????????=CD不能判断四边形ABCD是平行四边形,有可能是等腰梯形;
故本选项符合题意;
D、由?????????=CD,????????∥BC可以判断四边形ABCD是平行四边形;故本选项不符合题意,
故选C.
?
3.如图,?ABCD中E,F分别是AD,BC中点,AF与BE交于点G,CE和DF交于点H,求证:四边形EGFH是平行四边形.
【详解】
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵AE=????????AD,FC=????????BC,∴AE∥FC,AE=FC.
∴四边形AECF是平行四边形.∴GF∥EH.
同理可证:ED∥BF且ED=BF.
∴四边形BFDE是平行四边形.
∴GE∥FH.
∴四边形EGFH是平行四边形.
?
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴…是平行四边形
定理1
两组对边分别相等的四边形是平等四边形
∵AB=CD,AD= BC ∴…是平行四边形
定理2
对角线互相平分的四边形是平行四边形
∵OA=OC,OB=OD ∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
O
方法归纳:若条件集中在边上则选用定义法和定理1相对简单,若条件集中在对角线上,则选用定理2.
课堂小结
谢谢聆听
2021年春人教版八年级(下)数学
18.1.2 平行四边形的判定
第一课时
平行四边形性质知识点回顾
两组对边分别平行的四边形叫做平行四边形。
A
B
D
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
概念:
几何描述:
平行四边形对边相等
平行四边形对角相等
性质:
平行四边形对角线互相平分
1.平行四边形判定方法及应用。
2.综合运用平行四边形的判定和性质解决实际问题。
平行四边形判定方法及应用。(重点)
综合运用平行四边形的判定和性质解决实际问题。(难点)??
学习目标
探索与思考
A
B
D
C
平行四边形的性质:
平行四边形对边相等
平行四边形对角线互相平分
根据逆命题内容,尝试依次画出四边形,它们是平行四边形吗?
平行四边形对角相等
平行四边形性质的逆命题:
两组对边分别相等的四边形是平行四边形。
两组对角分别相等的四边形是平行四边形。
对角线互相平分的四边形是平行四边形。
探究新知
探索与证明
两组对边分别相等的四边形是平行四边形。
已知:四边形ABCD中,AD=BC,AB=CD
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
连接AC
∵ AB=CD,AD=BC,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
探索与证明
两组对角分别相等的四边形是平行四边形。
已知:在四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
A
B
D
C
∵∠A=∠C,∠B=∠D 而∠A+∠B+∠C+∠D=360°
∴∠A+∠B=180°,∠B+∠C=180°
∴AD∥BC,AB∥DC
∴四边形ABCD是平行四边形.
探索与证明
对角线互相平分的四边形是平行四边形。
已知:四边形ABCD中,AO=OC,BO=DO
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
O
∵AO=OC,BO=DO ,∠AOD = ∠COB ,
∴△AOD≌△COB(SAS).
∴∠1=∠3 ∴AD∥BC
同理 △AOB≌△COD(SAS).
∴ ∠2=∠4 ∴AB∥DC
∴四边形ABCD是平行四边形.
{00A15C55-8517-42AA-B614-E9B94910E393}
文字语言
图形语言
几何语言
定义法
两组对边分别平行的四边形是平行四边形
∵AB//CD, AD//BC,
∴四边形ABCD是平行四边形
判定方法1
两组对边分别相等的四边形是平行四边形
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形
判定方法2
两组对角分别相等的四边形是平行四边形
∵∠A= ∠C, ∠B= ∠D,
∴四边形ABCD是平行四边形
判定方法3
对角线互相平分的四边形是平行四边形
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
小结
1.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
【详解】
解:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.故选:A.
针对练习
2.如图,在平行四边形 ABCD中,点E、F在对角线BD上,且BE=DF.
(1)求证:AE=CF;
(2)求证:四边形AECF是平行四边形.
【详解】
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.∴∠ABE=∠CDF.
在△ABE和△CDF中,&????????=????????&∠????????????=∠????????????&????????=????????,
∴△ABE≌△DCF(SAS).
∴AE=CF.
?
(2)∵△ABE≌△DCF,
∴∠AEB=∠CFD,
∴∠AEF=∠CFE,
∴AE∥CF,
∵AE=CF,
∴四边形AECF是平行四边形.
探索与思考
若这个四边形的一组对边相等,还需添加什么条件(并尝试证明),则这个四边形是平行四边形。
已知:四边形ABCD中,AD=BC, ____?_____
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
连接AC
∵ AB=CD,AD=BC,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
条件一:AB=CD
探索与证明
若这个四边形的一组对边相等,还需添加什么条件(并尝试证明) ,则这个四边形是平行四边形。
已知:四边形ABCD中,AD=BC, ____?_____
求证:四边形ABCD是平行四边形
连接AC ∵AD∥BC ∴∠1=∠3
∵ AD=BC,∠1=∠3,AC=CA,
∴ △ABC≌△CDA(SAS).
∴ ∠2=∠4.
∴ AB∥DC 而AD∥BC
∴ 四边形ABCD是平行四边形.
条件二:AD∥BC
A
B
D
C
1
2
3
4
四边形ABCD中,AD=BC, AB∥CD,小明同学认为四边形ABCD是平行四边形?你认同吗?为什么?
小明的答案如下:
①连接AC ∵AB∥DC ∴∠2=∠4
②∵ AD=BC,AC=CA,∠2=∠4
③∴△ABC≌△CDA(SSA).
④∴∠1=∠3.
⑤∴AD∥BC而AB∥DC
⑥∴四边形ABCD是平行四边形.
A
B
D
C
1
2
3
4
探索与证明
1.如图,在?ABCD中,E、F分别是AB,CD的中点.
求证:四边形EBFD是平行四边形.
证明:∵四边形ABCD是平行四边形
∴AB=CD,EB//FD
又∵EB= ?????????AB,FD= ?????????CD
∴EB=FD
∴四边形EBFD是平行四边形.
?
课堂练习
2.下列选项中,不能判定四边形ABCD是平行四边形的是( )
A.????????∥BC, ????????∥CD B. ????????∥CD , ????????=CD
C.????????∥BC, ?????????=CD D. ?????????=CD ,????????∥BC
?
【详解】
A、由????????∥BC,????????∥CD可以判断四边形ABCD是平行四边形;故本选项不符合题意;
B、由????????∥CD,????????=CD可以判断四边形ABCD是平行四边形;故本选项不符合题意;
C、????????∥BC, ?????????=CD不能判断四边形ABCD是平行四边形,有可能是等腰梯形;
故本选项符合题意;
D、由?????????=CD,????????∥BC可以判断四边形ABCD是平行四边形;故本选项不符合题意,
故选C.
?
3.如图,?ABCD中E,F分别是AD,BC中点,AF与BE交于点G,CE和DF交于点H,求证:四边形EGFH是平行四边形.
【详解】
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵AE=????????AD,FC=????????BC,∴AE∥FC,AE=FC.
∴四边形AECF是平行四边形.∴GF∥EH.
同理可证:ED∥BF且ED=BF.
∴四边形BFDE是平行四边形.
∴GE∥FH.
∴四边形EGFH是平行四边形.
?
判定
文字语言
图形语言
符号语言
定义
两组对边分别平行的四边形是平行四边形
∵AB∥CD,AD∥BC
∴…是平行四边形
定理1
两组对边分别相等的四边形是平等四边形
∵AB=CD,AD= BC ∴…是平行四边形
定理2
对角线互相平分的四边形是平行四边形
∵OA=OC,OB=OD ∴…是平行四边形
A
B
C
D
A
B
C
D
A
B
C
D
O
方法归纳:若条件集中在边上则选用定义法和定理1相对简单,若条件集中在对角线上,则选用定理2.
课堂小结
谢谢聆听
