6.4.3(3)余弦定理、正弦定理应用举例-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习Word含解析
文档属性
| 名称 | 6.4.3(3)余弦定理、正弦定理应用举例-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册练习Word含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览



文档简介
6.4.3(3)余弦定理、正弦定理应用举例 同步练习
一.选择题
1.如图,设、两点在河的两岸,一测量者在的同侧所在的河岸边选定一点,测出的距离为,,后,就可以计算出、两点的距离为
A. B. C. D.
2.两灯塔、与海洋观察站的距离都等于,灯塔在观察站北偏东,灯塔在观察站南偏东,则、之间的距离是
A. B. C. D.
3.如图,在山脚测得山顶的仰角为,沿倾斜角为的斜坡向上走米到,在处测得山顶的仰角为,求山高
A. B. C. D.
4.当太阳光与水平面的倾斜角为时,一根长为的竹竿如图所示放置,要使它的影子最长,则竹竿与地面所成的角为
A. B. C. D.
5.一船自西向东航行,上午10时到达灯塔的南偏西、距塔68海里的处,下午2时到达这座灯塔的东南方向的处,则这只船航行的速度为
A.海里时 B.海里时 C.海里时 D.海里时
6.如图所示,为了测量某一隧道两侧、两地间的距离,某同学首先选定了不在直线上的一点中、、所对的边分别为、、,然后确定测量方案并测出相关数据,进行计算.现给出如下四种测量方案;①测量,,;②测量,,;③测量,;④测量,,,则一定能确定、间距离的所有方案的序号为
A.①③ B.①③④ C.②③④ D.①②④
7.如图,有四座城市、、、,其中在的正东方向,且与相距,在的北偏东方向,且与相距;在的北偏东方向,且与相距,一架飞机从城市出发以的速度向城市飞行,飞行了,接到命令改变航向,飞向城市,此时飞机距离城市有_______km(
A.120 B. C. D.
8.一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点测得水柱顶端的仰角为,沿点向北偏东前进100米到达点,在点测得水柱顶端的仰角为,则水柱的高度是
A.50米 B.60米 C.80米 D.100米
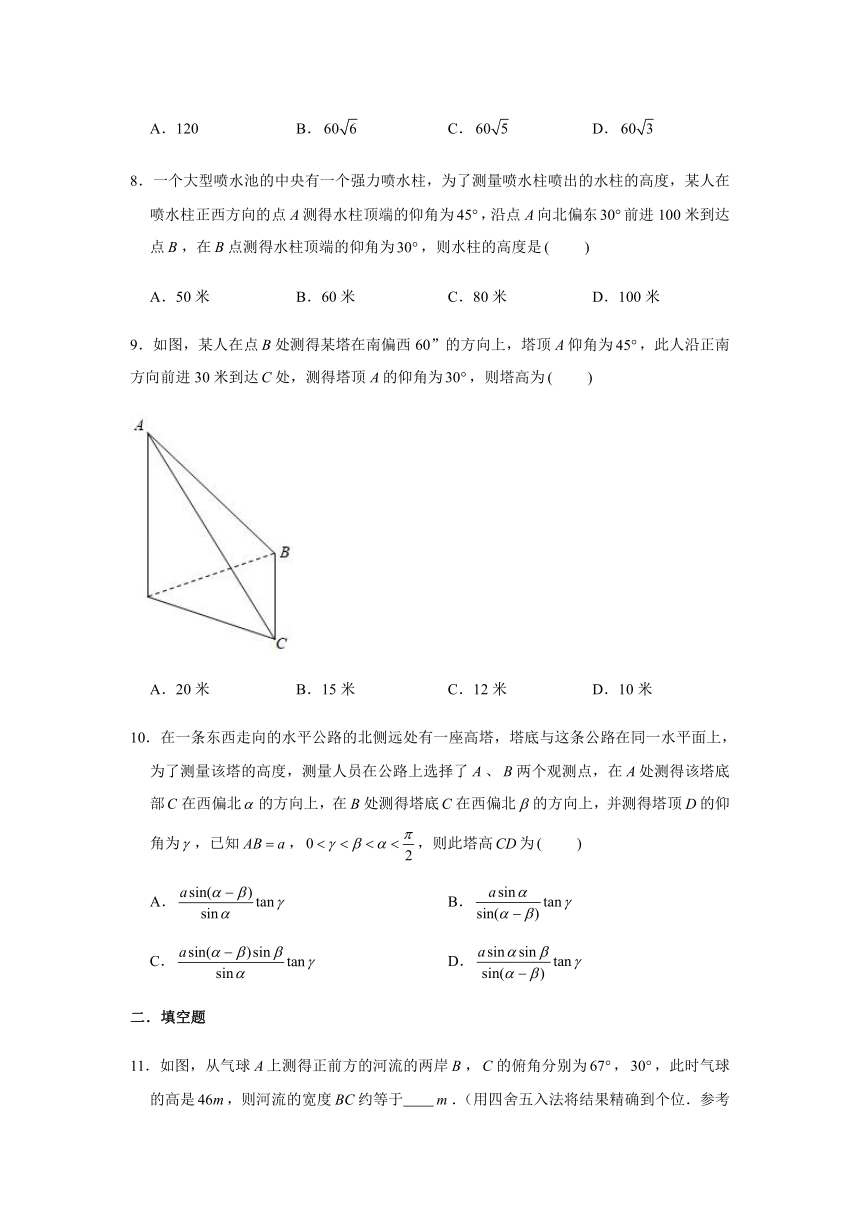
9.如图,某人在点处测得某塔在南偏西60”的方向上,塔顶仰角为,此人沿正南方向前进30米到达处,测得塔顶的仰角为,则塔高为
A.20米 B.15米 C.12米 D.10米
10.在一条东西走向的水平公路的北侧远处有一座高塔,塔底与这条公路在同一水平面上,为了测量该塔的高度,测量人员在公路上选择了、两个观测点,在处测得该塔底部在西偏北的方向上,在处测得塔底在西偏北的方向上,并测得塔顶的仰角为,已知,,则此塔高为
A. B.
C. D.
二.填空题
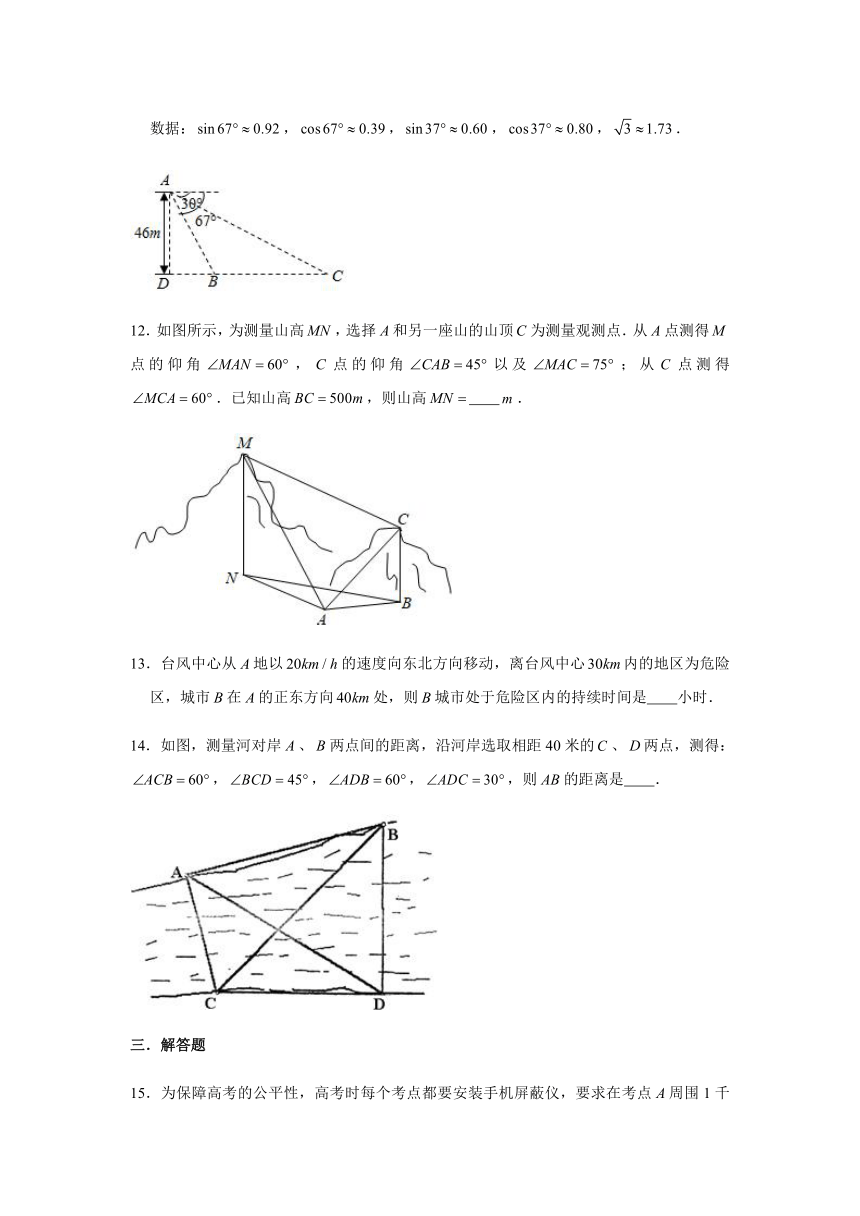
11.如图,从气球上测得正前方的河流的两岸,的俯角分别为,,此时气球的高是,则河流的宽度约等于 .(用四舍五入法将结果精确到个位.参考数据:,,,,.
12.如图所示,为测量山高,选择和另一座山的山顶为测量观测点.从点测得点的仰角,点的仰角以及;从点测得.已知山高,则山高 .
13.台风中心从地以的速度向东北方向移动,离台风中心内的地区为危险区,城市在的正东方向处,则城市处于危险区内的持续时间是 小时.
14.如图,测量河对岸、两点间的距离,沿河岸选取相距40米的、两点,测得:,,,,则的距离是 .
三.解答题
15.为保障高考的公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1千米处不能收到手机信号,检查员抽查青岛市一考点,在考点正西约千米处有一条北偏东方向的公路,在此处检查员用手机接通电话,以每小时12千米的速度沿公路行驶,问最长需要多少分钟检查员开始收不到信号,并至少持续多长时间该考点才算合格?
16.已知在东西方向上有,两座小山,山头上各有一个发射塔,,塔顶,的海拔高度分别为米和米,在水平面上有一条公路为西偏北方向,公路上有一测量车在小山的正南方向点处,测得发射塔顶的仰角,汽车沿公路西偏北方向行驶了米后在点处测得发射塔顶处的仰角为,且,经测量求两发射塔顶,的直线距离.
17.某海上养殖基地,接到气象部门预报,位于基地南偏东相距的海面上有一台风中心,影响半径为,正以的速度沿某一方向匀速直线前进,预计台风中心将从基地东北方向刮过且后开始影响基地持续,求台风移动的方向.
18.某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:、、三地位于同一水平面上,在处进行该仪器的垂直弹射,观测点、两地相距100米,,在地听到弹射声音的时间比在地晚秒.地测得该仪器弹至最高点时的仰角为.
(1)求、两地的距离;
(2)求该仪器的垂直弹射高度.(声音的传播速度为340米秒)
6.4.3(3)余弦定理、正弦定理应用举例 同步练习答案
1.解:在中,,,,
即,
则由正弦定理,
得:.
故选:.
2.解:依题意,作图如下:
,
,
由余弦定理得:
,
.
故选:.
3.解:设,
中,,,
,.
米.
故选:.
4.解:设竹竿与地面所成的角为,影子长为.由正弦定理,得,
所以,
因为,
所以当,即时,有最大值,故竹竿与地面所成的角为时,影子最长.
故选:.
5.解:由题意知,.
在中,由正弦定理,得
,
.
又由到所用时间为(小时),
船的航行速度(海里时);
故选:.
6.解:①由,可算出,再根据正弦定理:可计算出,
②已知三角,没有已知边,无论用正弦定理还是余弦定理都算不出,
③已知两边夹角,用余弦定理可计算出,
④已知两角,可计算出第三角,再用正弦定理可解得,
故选:.
7.解:在中,依题意可得,,,
,
.
,.
在中,..
设飞机在处改变航向,连接,则,
在中,.
故选:.
8.解:如图所示,
设水柱的高度为.
在中,,.
,.
在中,,.
在中,由余弦定理可得:.
,
化为,解得.
故选:.
9.解:如图,
设塔高为,
在中,,
则.
在中,
,则,
在中,
由余弦定理得:,
即,
,解得或(舍;
故选:.
10.解:在中,,,,
,
,
.
故选:.
二.填空题(共4小题)
11.解:过点作垂直于的延长线,垂足为,
则中,,,
,
根据正弦定理
得.
故答案为:60.
12.解:在中,,,所以;
在中,,,从而,
由正弦定理得,,
因此;
在中,,,
由,
得.
故答案为:750.
13.解:如图,以为坐标原点,建立平面直角坐标系,则,
台风中心移动的轨迹为射线,
而点到射线的距离,
故,
故城市处于危险区内的时间为1小时,
故答案为:1.
14.解:,,
,又,
为等腰直角三角形,又,
,
在中,,,
,
又,
由正弦定理得:,
解得:,
在中,利用余弦定理得:,
解得:.
故答案为:
15.解:根据题意,考点为、检查开始处为,设检查员行驶到直线上的、两点之间时收不到信号,
即公路上、两点到考点的距离为1千米,如右图所示,
在中,(千米),(千米),,
由正弦定理,
可得,不合题意),
,可得(千米),
中,,,
为等边三角形,可得(千米).
因此检查员在上行驶,需要分钟,在上行驶,需要分钟.
答:该检查员最长需要5分钟开始收不到信号,并持续至少5分钟才算合格.
16.解:在中,,
连接,在中,,
又
为等边三角形
在中,由得
又在中,,,
在中,
答:,两塔顶间的直线距离是米.
17.解:如图所示,设预报时台风中心为,开始影响基地时台风中心为,基地刚好不受影响时台风中心为,则、、在一直线上,且、,
由题意,,
在中,,
,
在中,由余弦定理得
,
又位于南偏东,,
位于的正北方向,
又,
台风移动的方向为向量的方向,即北偏西方向
答:台风向北偏西方向移动.
18.解:(1)由题意,设,
则.
在中,由余弦定理,得
,
即 ,解得.
、两地间的距离为.
(2)在中,,,
所以.
答:该仪器的垂直弹射高度为米.
一.选择题
1.如图,设、两点在河的两岸,一测量者在的同侧所在的河岸边选定一点,测出的距离为,,后,就可以计算出、两点的距离为
A. B. C. D.
2.两灯塔、与海洋观察站的距离都等于,灯塔在观察站北偏东,灯塔在观察站南偏东,则、之间的距离是
A. B. C. D.
3.如图,在山脚测得山顶的仰角为,沿倾斜角为的斜坡向上走米到,在处测得山顶的仰角为,求山高
A. B. C. D.
4.当太阳光与水平面的倾斜角为时,一根长为的竹竿如图所示放置,要使它的影子最长,则竹竿与地面所成的角为
A. B. C. D.
5.一船自西向东航行,上午10时到达灯塔的南偏西、距塔68海里的处,下午2时到达这座灯塔的东南方向的处,则这只船航行的速度为
A.海里时 B.海里时 C.海里时 D.海里时
6.如图所示,为了测量某一隧道两侧、两地间的距离,某同学首先选定了不在直线上的一点中、、所对的边分别为、、,然后确定测量方案并测出相关数据,进行计算.现给出如下四种测量方案;①测量,,;②测量,,;③测量,;④测量,,,则一定能确定、间距离的所有方案的序号为
A.①③ B.①③④ C.②③④ D.①②④
7.如图,有四座城市、、、,其中在的正东方向,且与相距,在的北偏东方向,且与相距;在的北偏东方向,且与相距,一架飞机从城市出发以的速度向城市飞行,飞行了,接到命令改变航向,飞向城市,此时飞机距离城市有_______km(
A.120 B. C. D.
8.一个大型喷水池的中央有一个强力喷水柱,为了测量喷水柱喷出的水柱的高度,某人在喷水柱正西方向的点测得水柱顶端的仰角为,沿点向北偏东前进100米到达点,在点测得水柱顶端的仰角为,则水柱的高度是
A.50米 B.60米 C.80米 D.100米
9.如图,某人在点处测得某塔在南偏西60”的方向上,塔顶仰角为,此人沿正南方向前进30米到达处,测得塔顶的仰角为,则塔高为
A.20米 B.15米 C.12米 D.10米
10.在一条东西走向的水平公路的北侧远处有一座高塔,塔底与这条公路在同一水平面上,为了测量该塔的高度,测量人员在公路上选择了、两个观测点,在处测得该塔底部在西偏北的方向上,在处测得塔底在西偏北的方向上,并测得塔顶的仰角为,已知,,则此塔高为
A. B.
C. D.
二.填空题
11.如图,从气球上测得正前方的河流的两岸,的俯角分别为,,此时气球的高是,则河流的宽度约等于 .(用四舍五入法将结果精确到个位.参考数据:,,,,.
12.如图所示,为测量山高,选择和另一座山的山顶为测量观测点.从点测得点的仰角,点的仰角以及;从点测得.已知山高,则山高 .
13.台风中心从地以的速度向东北方向移动,离台风中心内的地区为危险区,城市在的正东方向处,则城市处于危险区内的持续时间是 小时.
14.如图,测量河对岸、两点间的距离,沿河岸选取相距40米的、两点,测得:,,,,则的距离是 .
三.解答题
15.为保障高考的公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1千米处不能收到手机信号,检查员抽查青岛市一考点,在考点正西约千米处有一条北偏东方向的公路,在此处检查员用手机接通电话,以每小时12千米的速度沿公路行驶,问最长需要多少分钟检查员开始收不到信号,并至少持续多长时间该考点才算合格?
16.已知在东西方向上有,两座小山,山头上各有一个发射塔,,塔顶,的海拔高度分别为米和米,在水平面上有一条公路为西偏北方向,公路上有一测量车在小山的正南方向点处,测得发射塔顶的仰角,汽车沿公路西偏北方向行驶了米后在点处测得发射塔顶处的仰角为,且,经测量求两发射塔顶,的直线距离.
17.某海上养殖基地,接到气象部门预报,位于基地南偏东相距的海面上有一台风中心,影响半径为,正以的速度沿某一方向匀速直线前进,预计台风中心将从基地东北方向刮过且后开始影响基地持续,求台风移动的方向.
18.某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:、、三地位于同一水平面上,在处进行该仪器的垂直弹射,观测点、两地相距100米,,在地听到弹射声音的时间比在地晚秒.地测得该仪器弹至最高点时的仰角为.
(1)求、两地的距离;
(2)求该仪器的垂直弹射高度.(声音的传播速度为340米秒)
6.4.3(3)余弦定理、正弦定理应用举例 同步练习答案
1.解:在中,,,,
即,
则由正弦定理,
得:.
故选:.
2.解:依题意,作图如下:
,
,
由余弦定理得:
,
.
故选:.
3.解:设,
中,,,
,.
米.
故选:.
4.解:设竹竿与地面所成的角为,影子长为.由正弦定理,得,
所以,
因为,
所以当,即时,有最大值,故竹竿与地面所成的角为时,影子最长.
故选:.
5.解:由题意知,.
在中,由正弦定理,得
,
.
又由到所用时间为(小时),
船的航行速度(海里时);
故选:.
6.解:①由,可算出,再根据正弦定理:可计算出,
②已知三角,没有已知边,无论用正弦定理还是余弦定理都算不出,
③已知两边夹角,用余弦定理可计算出,
④已知两角,可计算出第三角,再用正弦定理可解得,
故选:.
7.解:在中,依题意可得,,,
,
.
,.
在中,..
设飞机在处改变航向,连接,则,
在中,.
故选:.
8.解:如图所示,
设水柱的高度为.
在中,,.
,.
在中,,.
在中,由余弦定理可得:.
,
化为,解得.
故选:.
9.解:如图,
设塔高为,
在中,,
则.
在中,
,则,
在中,
由余弦定理得:,
即,
,解得或(舍;
故选:.
10.解:在中,,,,
,
,
.
故选:.
二.填空题(共4小题)
11.解:过点作垂直于的延长线,垂足为,
则中,,,
,
根据正弦定理
得.
故答案为:60.
12.解:在中,,,所以;
在中,,,从而,
由正弦定理得,,
因此;
在中,,,
由,
得.
故答案为:750.
13.解:如图,以为坐标原点,建立平面直角坐标系,则,
台风中心移动的轨迹为射线,
而点到射线的距离,
故,
故城市处于危险区内的时间为1小时,
故答案为:1.
14.解:,,
,又,
为等腰直角三角形,又,
,
在中,,,
,
又,
由正弦定理得:,
解得:,
在中,利用余弦定理得:,
解得:.
故答案为:
15.解:根据题意,考点为、检查开始处为,设检查员行驶到直线上的、两点之间时收不到信号,
即公路上、两点到考点的距离为1千米,如右图所示,
在中,(千米),(千米),,
由正弦定理,
可得,不合题意),
,可得(千米),
中,,,
为等边三角形,可得(千米).
因此检查员在上行驶,需要分钟,在上行驶,需要分钟.
答:该检查员最长需要5分钟开始收不到信号,并持续至少5分钟才算合格.
16.解:在中,,
连接,在中,,
又
为等边三角形
在中,由得
又在中,,,
在中,
答:,两塔顶间的直线距离是米.
17.解:如图所示,设预报时台风中心为,开始影响基地时台风中心为,基地刚好不受影响时台风中心为,则、、在一直线上,且、,
由题意,,
在中,,
,
在中,由余弦定理得
,
又位于南偏东,,
位于的正北方向,
又,
台风移动的方向为向量的方向,即北偏西方向
答:台风向北偏西方向移动.
18.解:(1)由题意,设,
则.
在中,由余弦定理,得
,
即 ,解得.
、两地间的距离为.
(2)在中,,,
所以.
答:该仪器的垂直弹射高度为米.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
