2020-2021学年人教版数学八年级第下册第十八章《平行四边形》单元复习卷(word版,含答案)
文档属性
| 名称 | 2020-2021学年人教版数学八年级第下册第十八章《平行四边形》单元复习卷(word版,含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 07:56:22 | ||
图片预览

文档简介
2020-2021学年人教版八年级第二学期第十八章 平行四边形 单元卷
一、单选题
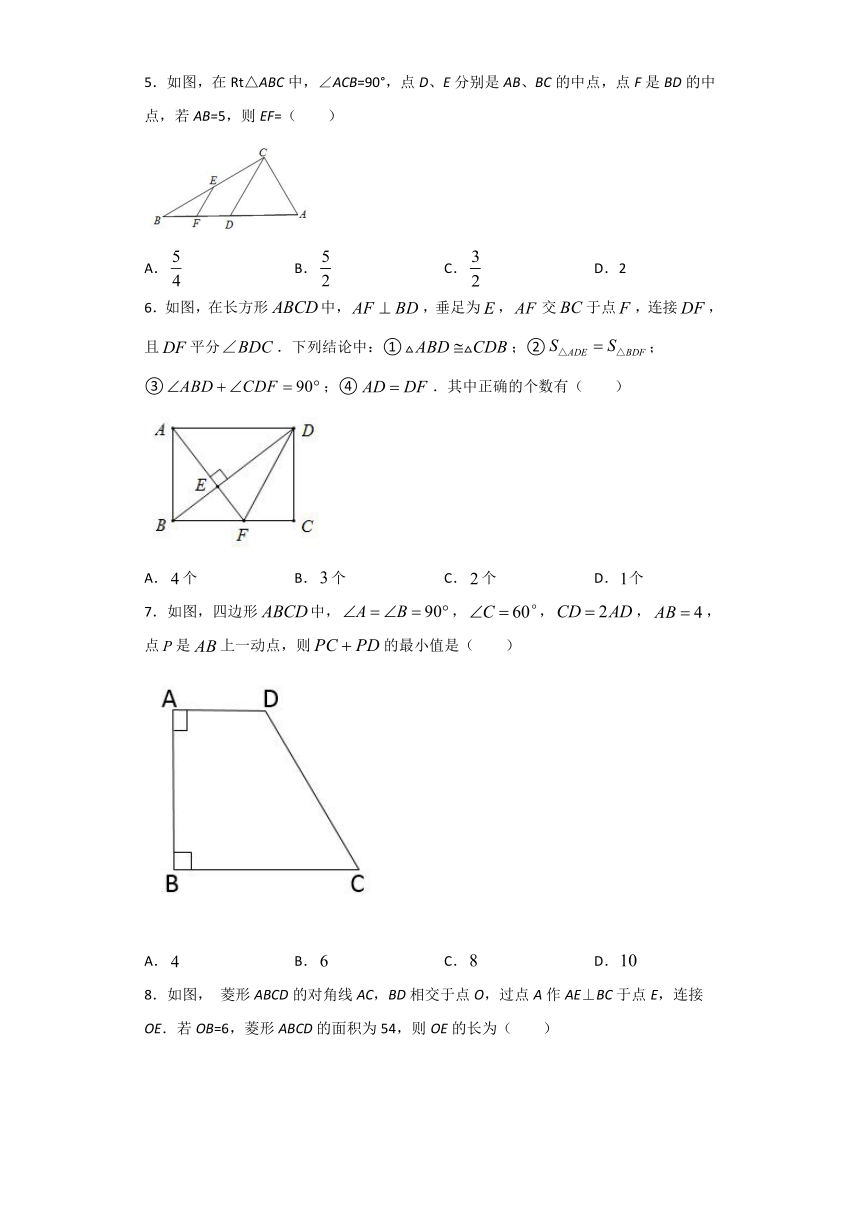
1.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是( )
A.60 B.30 C.20 D.16
2.如图,是的边延长线上一点,连接,,,交于点,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
3.如图,把矩形沿对折,若则等于( )
A. B. C. D.
4.如图,ABE、BCF、CDG、DAH是四个全等的直角三角形,其中,AE=5,AB=13,则EG的长是( )
A.7 B.6 C.7 D.7
5.如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F是BD的中点,若AB=5,则EF=( )
A. B. C. D.2
6.如图,在长方形中,,垂足为,交于点,连接,且平分.下列结论中:①;②;③;④.其中正确的个数有( )
A.个 B.个 C.个 D.个
7.如图,四边形中,,,,,点是上一动点,则的最小值是( )
A. B. C. D.
8.如图, 菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连接OE.若OB=6,菱形ABCD的面积为54,则OE的长为( )
A.4 B.4.5 C.8 D.9
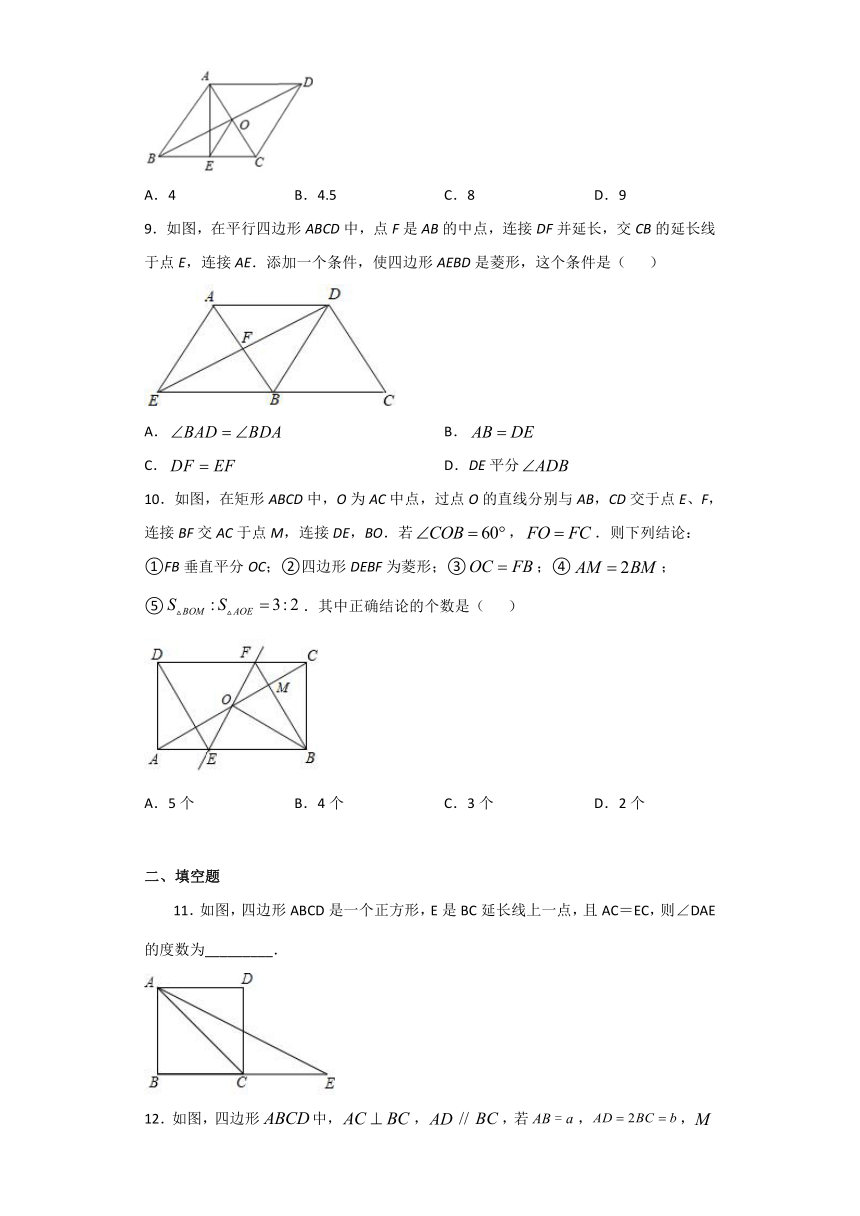
9.如图,在平行四边形ABCD中,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.添加一个条件,使四边形AEBD是菱形,这个条件是( )
A. B.
C. D.DE平分
10.如图,在矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E、F,连接BF交AC于点M,连接DE,BO.若,.则下列结论:①FB垂直平分OC;②四边形DEBF为菱形;③;④;⑤.其中正确结论的个数是( )
A.5个 B.4个 C.3个 D.2个
二、填空题
11.如图,四边形ABCD是一个正方形,E是BC延长线上一点,且AC=EC,则∠DAE的度数为_________.
12.如图,四边形中,,,若,,为的中点,则的长为_______.
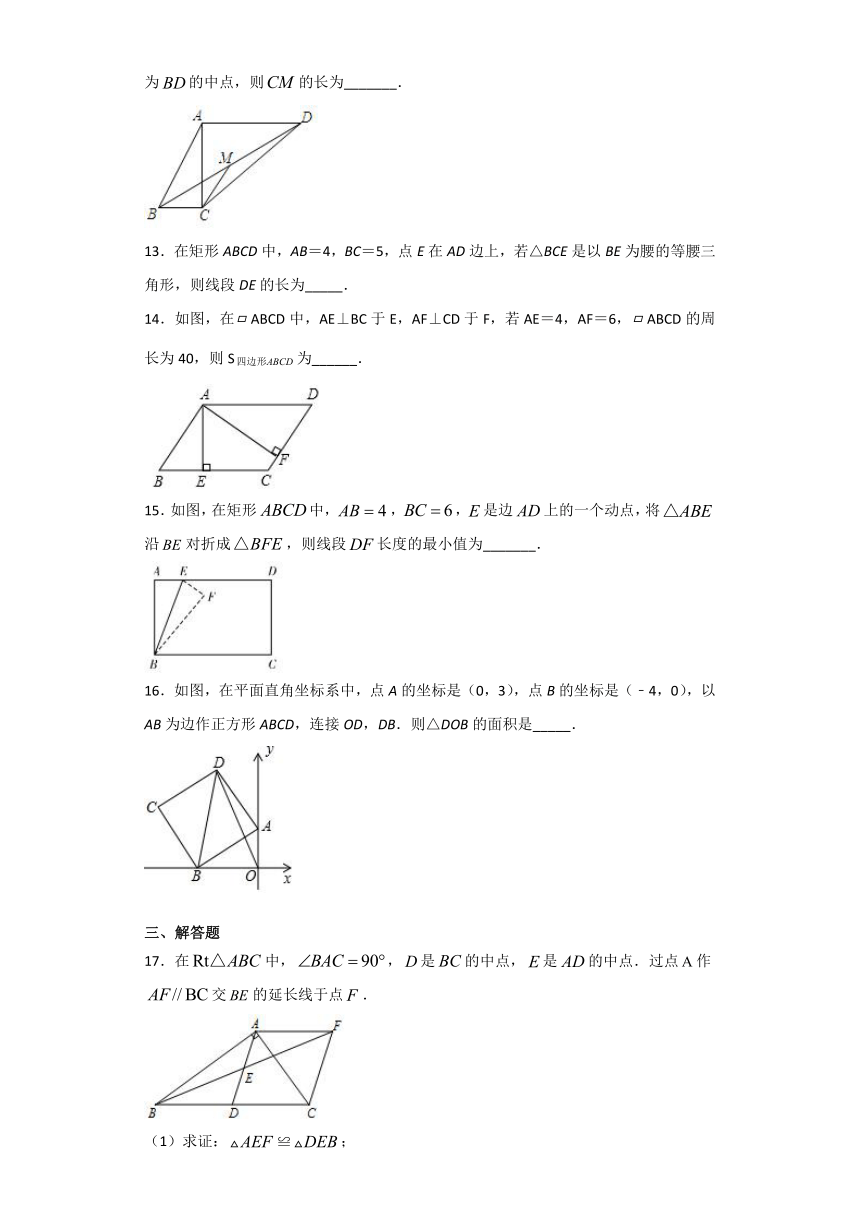
13.在矩形ABCD中,AB=4,BC=5,点E在AD边上,若△BCE是以BE为腰的等腰三角形,则线段DE的长为_____.
14.如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
15.如图,在矩形中,,,是边上的一个动点,将沿对折成,则线段长度的最小值为_______.
16.如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是_____.
三、解答题
17.在中,,是的中点,是的中点.过点作交的延长线于点.
(1)求证:≌;
(2)证明四边形是菱形.
18.如图,在平行四边形中,对角线相交于点O,点E,F在上,且.
(1)求证:;
(2)不添加辅助线,请你补充一个条件,使得四边形是菱形;并给予证明.
19.如图,在中,是边的中点,的延长线与的延长线相交于点.
求证:.
20.如图,在平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.
(1)求证:AEF≌DEC;
(2)求证:四边形ACDF是平行四边形.
21.在中,,分别为对角线上两点,连接,,,,并且.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,若,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于面积的.
22.如图,在直角坐标系中,四边形OABC是矩形,OA=8,OC=6,点D是对角线AC的中点,过点D的直线分别交OA、BC边于点E、F.
(1)求证:四边形EAFC是平行四边形;
(2)当CE=CF时,求EF的长;
(3)在条件(2)的情况下,P为x轴上一点,当以E,F,P为顶点的三角形为等腰三角形时,请求出点P的坐标.
参考答案
1.C
【详解】
解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC-BE=6-2=4,
∴CD=AB=4,
∴?ABCD的周长=6+6+4+4=20.
故选:C.
2.A
【详解】
解:A、∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故A错误;
∵ DE∥BC,
∴∠DEF=∠CBF,
∠DEF=∠CBF
在△DEF与△CBF中,
∴△DEF△CBF(ASA),
∴DF=CF
∵EF=BF
∴四边形BCED为平行四边形,故B正确;
∵四边形ABCD是平行四边形,
∴ .AD∥BC,AB∥CD,
∴DE∥CE,∠ABD=∠CDB,
∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴四边形BCED为平行四边形,故C正确;
∵AEB∥C,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D正确.
故选:A.
3.B
【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEF+∠BFE=180°,
∵,
∴∠BFE=68°,
∴∠1=180°-2∠BFE=44°,
故选B.
4.A
【详解】
解:在Rt△ABE中,AE=5,AB=13,
由勾股定理得,BE===12,
∵△ABE、△BCF、△CDG、△DAH是四个全等的直角三角形,
∴∠AEB=∠BFC=∠CGD=90°,BF=CG=DH=AE=5,
∴∠FEB=∠EFC=∠FGD=90°,EF=EH=12﹣5=7,
∴四边形EFGH为正方形,
∴EG==7,
故选:A.
5.A
【详解】
解:∵∠ACB=90°,AB=5,点D是AB的中点,
∴,
∵点E、F分别是BC、BD的中点,
∴;
故选A.
6.C
【详解】
解: 长方形,
故①符合题意;
平分,
故②符合题意;
长方形,
若,
是的中点,
是的垂直平分线,
则四边形为正方形,与已知互相矛盾,故③不符合题意;
若,
是的垂直平分线,
则四边形为正方形,与已知互相矛盾,故④不符合题意;
故选:
7.C
【详解】
作D点关于AB的对称点D',连接CD'交AB于P,P即为所求,此时PC+PD=PC+PD'=CD',根据两点之间线段最短可知此时PC+PD最小.
作D'E⊥BC于E,则EB=D'A=AD.
∵CD=2AD,
∴DD'=CD,
∴∠DCD'=∠DD'C.
∵∠DAB=∠ABC=90°,
∴四边形ABED'是矩形,
∴DD'∥EC,D'E=AB=4,
∴∠D'CE=∠DD'C,
∴∠D'CE=∠DCD'.
∵∠DCB=60°,
∴∠D'CE=30°,
∴在Rt△D'CE中,D'C=2D'E=2×4=8,
∴PC+PD的最小值为8.
故选:C.
8.B
【详解】
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD=BD,BD⊥AC,
∴BD=2OB=12,
∵S菱形ABCD═AC×BD=54,
∴AC=9,
∵AE⊥BC,
∴∠AEC=90°,
∴OE=AC=4.5,
故选:B.
9.D
【详解】
解:在平行四边形ABCD中,AD∥BC,
∴∠DAB=∠EBA,
∵点F是AB的中点,
∴AF=BF,
∵∠AFD=∠BFE,
∴△ADF≌△BEF,
∴AD=BE,
∵AD∥BE,
∴四边形AEBD是平行四边形,
A、当时,得到AB=BD,无法判定四边形AEBD是菱形,故该选项不符合题意;
B、AB=BE时,无法判定四边形AEBD是菱形,故该选项不符合题意;
C、DF=EF时,无法判定四边形AEBD是菱形,故该选项不符合题意;
D、当DE平分时,四边形AEBD是菱形,故该选项符合题意;
故选:D.
10.C
【详解】
连接BD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
∵FO=FC,BF=BF
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM;
∴①正确,
∵AB∥CD,
∴∠OCF=∠OAE,
∵OA=OC,
∴△AOE≌△COF,
∴OE=OF,FC=AE,
∴DF=BE,DF∥BE,
∴四边形EBFD是平行四边形,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵FO=OE=FC=AE,
∴∠AOE=∠FOM=30°,
∴∠BOF=90°,
∴BE=BF,
∴四边形EBFD是菱形,
∴结论②正确;
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵FO=OE=FC=AE,
∴∠AOE=∠FOM=30°,
∴∠BOF=90°,
∴FB>OB,
∵OB=OC,
∴FB>OC,
∴③错误,
在直角三角形AMB中,
∵∠BAM=30°,∠AMB=90°,
∴AB=2BM,
∴④错误,
设ED与AC的交点为N,
设AE=OE=2x,
则NE=x,BE=4x,
∴AB=6x,
∴BM=3x,
∴
=
=3:2,
结论⑤正确.
故选C.
11.22.5°
【详解】
解:∵四边形是正方形,
∴,
∴,
又∵,
∴,
则.
故答案为:22.5°
12.
【详解】
解:延长,使,
四边形是平行四边形,
∴DE=AB,
是的中点,
为的中点,
故答案为:.
13.2.5或2.
【详解】
解:∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=5,
①当BE=EC时,点E是BC的中垂线与AD的交点,
由轴对称的性质可得:;
②当时,
在中,AB=4,
则
∴
综上所述,线段DE的长为2.5或2,
故答案是:2.5或2.
14.48
【详解】
解:设BC=x,CD=y,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵?ABCD的周长为40,
∴x+y=20,
∵AE=4,AF=6,S=BC×AE=CD×AF,
∴4x=6y,
得方程组:,
解得:
∴S平行四边形ABCD=BC×AE=12×4=48.
故答案为:48.
15.
【详解】
如图,连接DF、BD,
由图可知,DF>BD-BF,
当点F落在BD上时,DF取得最小值,且最小值为BD-BF的长,
∵四边形ABCD是矩形,
∴AB=CD=4、BC=6,
∴BD=,
由折叠性质知AB=BF=4,
∴线段DF长度的最小值为BD-BF,
故答案为:..
16.14
【详解】
解:过点D作DE⊥y轴,垂足为E.
∵A的坐标是,点B的坐标是,
∴OA=3,OB=4.
∵ABCD为正方形,
∴AB=AD,∠DAB=90°.
∵,,
∴.
在和中,
∴.
∴AE=OB=4.
∴.
∴的面积=OB?OE=×4×7=14.
故答案为:14.
17.
【详解】
(1)∵,
∴,
∵是中点,是边上的中线,
∴,,
在和中,
,
∴≌(AAS).
(2)由(1)知≌,
则,
∵,
∴,
∵,
∴四边形是平行四边形,
∵,是的中点,是中点,
∴,
∴四边形是菱形.
18.
【详解】
(1)证明:∵四边形是平行四边形,
∴.
∴.
又∵,
∴.
(2)补充的条件是:.(答案不唯一)
证明:∵四边形是平行四边形,
∴,.
∵,
∴.
∴四边形是平行四边形.
又∵,
∴四边形是菱形.
19.
【详解】
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠F=∠EBA,
∵E是AD边的中点,
∴DE=AE,
在△DEF和△AEB中,
,
∴△DEF≌△AEB(AAS),
∴DF=AB,
∴DC=DF.
20.
【详解】
(1)∵在平行四边形ABCD中,AB∥CD,
∴∠FAE=∠CDE,
∵点E是边AD的中点,
∴AE=DE,
在△AEF和△DEC中,
∴△AEF≌△DEC(ASA).
(2)∵△AEF≌△DEC,
∴AF=DC,
∵AF∥DC,
∴四边形ACDF是平行四边形.
21.
(1)证明:如图1,
∵四边形为平行四边形,
∴,,
∵,
∴,
∴,即,
∴,
∴,
∴四边形是平行四边形;
(2)由(1)可得,BE=DF,
∵,
∴,
根据△ABD和△ABE、△ADF是等高,可得:△ABE、△ADF的面积是△ABD面积的,
∵四边形ABCD是平行四边形,
∴△ABD和△BCD的面积相等,
同理可得△BEC和△DFC的面积是△BCD面积的,
∴,,,的面积都等于面积的.
22.
【详解】
(1)证明:∵四边形OABC是矩形,
∴BC∥OA,
∴∠FCD=∠DAE,∠CFD=∠AED,
∵D是AC的中点,
∴CD=AD,
∴△CDF≌△ADE(AAS),
∴DF=DE,
∴四边形EAFC是平行四边形;
(2)解:∵四边形EAFC是平行四边形,CE=CF,
∴四边形EAFC是菱形,
∴CE=EA,AC⊥EF,
设CE=AE=x,
∵OC2+OE2=CE2,
∴62+(8﹣x)2=x2,
∴x=,
∴CE=,
∵OA=8,OC=6,
∴AC===10,
∴CD=AC=5,
∴ED===,
∴EF=2ED=;
(3)由(2)可知,,
分三种情况:
①若PE=PF,点P与点A重合,
∴P(8,0),
②若EF=EP=,
当点P在x轴的正半轴上,OP=OE+PE==,
∴P(,0),
当点P在x轴的负半轴上,OP=PE﹣OE==,
∴P(﹣,0),
③若EF=FP,过点F作FG⊥AE于点G,则EG=CF﹣OE=﹣=,
∴EP=9,
∴OP=OE+EP=+9=,
∴P(,0).
综上可得,点P的坐标为(8,0)或(,0)或(﹣,0)或(,0).
一、单选题
1.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是( )
A.60 B.30 C.20 D.16
2.如图,是的边延长线上一点,连接,,,交于点,添加以下条件,不能判定四边形为平行四边形的是( )
A. B. C. D.
3.如图,把矩形沿对折,若则等于( )
A. B. C. D.
4.如图,ABE、BCF、CDG、DAH是四个全等的直角三角形,其中,AE=5,AB=13,则EG的长是( )
A.7 B.6 C.7 D.7
5.如图,在Rt△ABC中,∠ACB=90°,点D、E分别是AB、BC的中点,点F是BD的中点,若AB=5,则EF=( )
A. B. C. D.2
6.如图,在长方形中,,垂足为,交于点,连接,且平分.下列结论中:①;②;③;④.其中正确的个数有( )
A.个 B.个 C.个 D.个
7.如图,四边形中,,,,,点是上一动点,则的最小值是( )
A. B. C. D.
8.如图, 菱形ABCD的对角线AC,BD相交于点O,过点A作AE⊥BC于点E,连接OE.若OB=6,菱形ABCD的面积为54,则OE的长为( )
A.4 B.4.5 C.8 D.9
9.如图,在平行四边形ABCD中,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.添加一个条件,使四边形AEBD是菱形,这个条件是( )
A. B.
C. D.DE平分
10.如图,在矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E、F,连接BF交AC于点M,连接DE,BO.若,.则下列结论:①FB垂直平分OC;②四边形DEBF为菱形;③;④;⑤.其中正确结论的个数是( )
A.5个 B.4个 C.3个 D.2个
二、填空题
11.如图,四边形ABCD是一个正方形,E是BC延长线上一点,且AC=EC,则∠DAE的度数为_________.
12.如图,四边形中,,,若,,为的中点,则的长为_______.
13.在矩形ABCD中,AB=4,BC=5,点E在AD边上,若△BCE是以BE为腰的等腰三角形,则线段DE的长为_____.
14.如图,在ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,ABCD的周长为40,则S为______.
15.如图,在矩形中,,,是边上的一个动点,将沿对折成,则线段长度的最小值为_______.
16.如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是_____.
三、解答题
17.在中,,是的中点,是的中点.过点作交的延长线于点.
(1)求证:≌;
(2)证明四边形是菱形.
18.如图,在平行四边形中,对角线相交于点O,点E,F在上,且.
(1)求证:;
(2)不添加辅助线,请你补充一个条件,使得四边形是菱形;并给予证明.
19.如图,在中,是边的中点,的延长线与的延长线相交于点.
求证:.
20.如图,在平行四边形ABCD中,点E是边AD的中点,连接CE并延长交BA的延长线于点F,连接AC,DF.
(1)求证:AEF≌DEC;
(2)求证:四边形ACDF是平行四边形.
21.在中,,分别为对角线上两点,连接,,,,并且.
(1)如图1,求证:四边形是平行四边形;
(2)如图2,若,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于面积的.
22.如图,在直角坐标系中,四边形OABC是矩形,OA=8,OC=6,点D是对角线AC的中点,过点D的直线分别交OA、BC边于点E、F.
(1)求证:四边形EAFC是平行四边形;
(2)当CE=CF时,求EF的长;
(3)在条件(2)的情况下,P为x轴上一点,当以E,F,P为顶点的三角形为等腰三角形时,请求出点P的坐标.
参考答案
1.C
【详解】
解:∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵?ABCD中,AD∥BC,
∴∠ADE=∠CED,
∴∠CDE=∠CED,
∴CE=CD,
∵在?ABCD中,AD=6,BE=2,
∴AD=BC=6,
∴CE=BC-BE=6-2=4,
∴CD=AB=4,
∴?ABCD的周长=6+6+4+4=20.
故选:C.
2.A
【详解】
解:A、∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故A错误;
∵ DE∥BC,
∴∠DEF=∠CBF,
∠DEF=∠CBF
在△DEF与△CBF中,
∴△DEF△CBF(ASA),
∴DF=CF
∵EF=BF
∴四边形BCED为平行四边形,故B正确;
∵四边形ABCD是平行四边形,
∴ .AD∥BC,AB∥CD,
∴DE∥CE,∠ABD=∠CDB,
∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴四边形BCED为平行四边形,故C正确;
∵AEB∥C,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故D正确.
故选:A.
3.B
【详解】
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AEF+∠BFE=180°,
∵,
∴∠BFE=68°,
∴∠1=180°-2∠BFE=44°,
故选B.
4.A
【详解】
解:在Rt△ABE中,AE=5,AB=13,
由勾股定理得,BE===12,
∵△ABE、△BCF、△CDG、△DAH是四个全等的直角三角形,
∴∠AEB=∠BFC=∠CGD=90°,BF=CG=DH=AE=5,
∴∠FEB=∠EFC=∠FGD=90°,EF=EH=12﹣5=7,
∴四边形EFGH为正方形,
∴EG==7,
故选:A.
5.A
【详解】
解:∵∠ACB=90°,AB=5,点D是AB的中点,
∴,
∵点E、F分别是BC、BD的中点,
∴;
故选A.
6.C
【详解】
解: 长方形,
故①符合题意;
平分,
故②符合题意;
长方形,
若,
是的中点,
是的垂直平分线,
则四边形为正方形,与已知互相矛盾,故③不符合题意;
若,
是的垂直平分线,
则四边形为正方形,与已知互相矛盾,故④不符合题意;
故选:
7.C
【详解】
作D点关于AB的对称点D',连接CD'交AB于P,P即为所求,此时PC+PD=PC+PD'=CD',根据两点之间线段最短可知此时PC+PD最小.
作D'E⊥BC于E,则EB=D'A=AD.
∵CD=2AD,
∴DD'=CD,
∴∠DCD'=∠DD'C.
∵∠DAB=∠ABC=90°,
∴四边形ABED'是矩形,
∴DD'∥EC,D'E=AB=4,
∴∠D'CE=∠DD'C,
∴∠D'CE=∠DCD'.
∵∠DCB=60°,
∴∠D'CE=30°,
∴在Rt△D'CE中,D'C=2D'E=2×4=8,
∴PC+PD的最小值为8.
故选:C.
8.B
【详解】
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD=BD,BD⊥AC,
∴BD=2OB=12,
∵S菱形ABCD═AC×BD=54,
∴AC=9,
∵AE⊥BC,
∴∠AEC=90°,
∴OE=AC=4.5,
故选:B.
9.D
【详解】
解:在平行四边形ABCD中,AD∥BC,
∴∠DAB=∠EBA,
∵点F是AB的中点,
∴AF=BF,
∵∠AFD=∠BFE,
∴△ADF≌△BEF,
∴AD=BE,
∵AD∥BE,
∴四边形AEBD是平行四边形,
A、当时,得到AB=BD,无法判定四边形AEBD是菱形,故该选项不符合题意;
B、AB=BE时,无法判定四边形AEBD是菱形,故该选项不符合题意;
C、DF=EF时,无法判定四边形AEBD是菱形,故该选项不符合题意;
D、当DE平分时,四边形AEBD是菱形,故该选项符合题意;
故选:D.
10.C
【详解】
连接BD,
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
∵FO=FC,BF=BF
∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM;
∴①正确,
∵AB∥CD,
∴∠OCF=∠OAE,
∵OA=OC,
∴△AOE≌△COF,
∴OE=OF,FC=AE,
∴DF=BE,DF∥BE,
∴四边形EBFD是平行四边形,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵FO=OE=FC=AE,
∴∠AOE=∠FOM=30°,
∴∠BOF=90°,
∴BE=BF,
∴四边形EBFD是菱形,
∴结论②正确;
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵FO=OE=FC=AE,
∴∠AOE=∠FOM=30°,
∴∠BOF=90°,
∴FB>OB,
∵OB=OC,
∴FB>OC,
∴③错误,
在直角三角形AMB中,
∵∠BAM=30°,∠AMB=90°,
∴AB=2BM,
∴④错误,
设ED与AC的交点为N,
设AE=OE=2x,
则NE=x,BE=4x,
∴AB=6x,
∴BM=3x,
∴
=
=3:2,
结论⑤正确.
故选C.
11.22.5°
【详解】
解:∵四边形是正方形,
∴,
∴,
又∵,
∴,
则.
故答案为:22.5°
12.
【详解】
解:延长,使,
四边形是平行四边形,
∴DE=AB,
是的中点,
为的中点,
故答案为:.
13.2.5或2.
【详解】
解:∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=5,
①当BE=EC时,点E是BC的中垂线与AD的交点,
由轴对称的性质可得:;
②当时,
在中,AB=4,
则
∴
综上所述,线段DE的长为2.5或2,
故答案是:2.5或2.
14.48
【详解】
解:设BC=x,CD=y,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∵?ABCD的周长为40,
∴x+y=20,
∵AE=4,AF=6,S=BC×AE=CD×AF,
∴4x=6y,
得方程组:,
解得:
∴S平行四边形ABCD=BC×AE=12×4=48.
故答案为:48.
15.
【详解】
如图,连接DF、BD,
由图可知,DF>BD-BF,
当点F落在BD上时,DF取得最小值,且最小值为BD-BF的长,
∵四边形ABCD是矩形,
∴AB=CD=4、BC=6,
∴BD=,
由折叠性质知AB=BF=4,
∴线段DF长度的最小值为BD-BF,
故答案为:..
16.14
【详解】
解:过点D作DE⊥y轴,垂足为E.
∵A的坐标是,点B的坐标是,
∴OA=3,OB=4.
∵ABCD为正方形,
∴AB=AD,∠DAB=90°.
∵,,
∴.
在和中,
∴.
∴AE=OB=4.
∴.
∴的面积=OB?OE=×4×7=14.
故答案为:14.
17.
【详解】
(1)∵,
∴,
∵是中点,是边上的中线,
∴,,
在和中,
,
∴≌(AAS).
(2)由(1)知≌,
则,
∵,
∴,
∵,
∴四边形是平行四边形,
∵,是的中点,是中点,
∴,
∴四边形是菱形.
18.
【详解】
(1)证明:∵四边形是平行四边形,
∴.
∴.
又∵,
∴.
(2)补充的条件是:.(答案不唯一)
证明:∵四边形是平行四边形,
∴,.
∵,
∴.
∴四边形是平行四边形.
又∵,
∴四边形是菱形.
19.
【详解】
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠F=∠EBA,
∵E是AD边的中点,
∴DE=AE,
在△DEF和△AEB中,
,
∴△DEF≌△AEB(AAS),
∴DF=AB,
∴DC=DF.
20.
【详解】
(1)∵在平行四边形ABCD中,AB∥CD,
∴∠FAE=∠CDE,
∵点E是边AD的中点,
∴AE=DE,
在△AEF和△DEC中,
∴△AEF≌△DEC(ASA).
(2)∵△AEF≌△DEC,
∴AF=DC,
∵AF∥DC,
∴四边形ACDF是平行四边形.
21.
(1)证明:如图1,
∵四边形为平行四边形,
∴,,
∵,
∴,
∴,即,
∴,
∴,
∴四边形是平行四边形;
(2)由(1)可得,BE=DF,
∵,
∴,
根据△ABD和△ABE、△ADF是等高,可得:△ABE、△ADF的面积是△ABD面积的,
∵四边形ABCD是平行四边形,
∴△ABD和△BCD的面积相等,
同理可得△BEC和△DFC的面积是△BCD面积的,
∴,,,的面积都等于面积的.
22.
【详解】
(1)证明:∵四边形OABC是矩形,
∴BC∥OA,
∴∠FCD=∠DAE,∠CFD=∠AED,
∵D是AC的中点,
∴CD=AD,
∴△CDF≌△ADE(AAS),
∴DF=DE,
∴四边形EAFC是平行四边形;
(2)解:∵四边形EAFC是平行四边形,CE=CF,
∴四边形EAFC是菱形,
∴CE=EA,AC⊥EF,
设CE=AE=x,
∵OC2+OE2=CE2,
∴62+(8﹣x)2=x2,
∴x=,
∴CE=,
∵OA=8,OC=6,
∴AC===10,
∴CD=AC=5,
∴ED===,
∴EF=2ED=;
(3)由(2)可知,,
分三种情况:
①若PE=PF,点P与点A重合,
∴P(8,0),
②若EF=EP=,
当点P在x轴的正半轴上,OP=OE+PE==,
∴P(,0),
当点P在x轴的负半轴上,OP=PE﹣OE==,
∴P(﹣,0),
③若EF=FP,过点F作FG⊥AE于点G,则EG=CF﹣OE=﹣=,
∴EP=9,
∴OP=OE+EP=+9=,
∴P(,0).
综上可得,点P的坐标为(8,0)或(,0)或(﹣,0)或(,0).
