2020-2021学年八年级数学沪教版下册压轴题集第四讲 菱形与正方形(Word版 无答案)
文档属性
| 名称 | 2020-2021学年八年级数学沪教版下册压轴题集第四讲 菱形与正方形(Word版 无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 913.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-18 23:09:48 | ||
图片预览


文档简介
八年级年级数学压轴题集
第四讲
菱形与正方形
1、菱形
【要点导航】
菱形是初中平面几何的一个重要内容.也是中考必考内容之--.菱形作为特殊的平行四边形关于边、角、对角线的性质丰富.有三种判定方法.这三种判定方法可划分为两类:一类与四边形的边有关:另一类与四边形的对角线有关.若已知条件出现在四边形的边上.则应考虑:一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形.若已知条件出现在四边形的对角线上.则应考虑:对角线垂直的平行四边形是菱形.
【典型例题】
【例1】
如图1所示.EF是矩形ABCD的对角线AC的垂直平分线.EF与对角线AC及边AD、BC分别交于点O、E、F.
(1)求证:四边形AFCE是菱形.
(2)如果FE=2ED.求AE
:
DE的值.
思路分析
(1)先证明△AOE≌OCOF
.得到对角线互相垂直平分.对角线互相平分的四边形是平行四边形,对角线互相垂.直的平行四边形是菱形.
(2)由第(1)小题的结论易得FO=EO=
ED.所以∠2=∠3=
∠4=30°.因此,图中所有的直角三角形均为含30°角的特殊直角三角形,再利用它们三边之比,便能求得AE
:
DE的值.
方法点睛
在△ACD中,CE平分2
LACD,由角平分线定理得AC与CD的比值等于AE与ED
的比值.
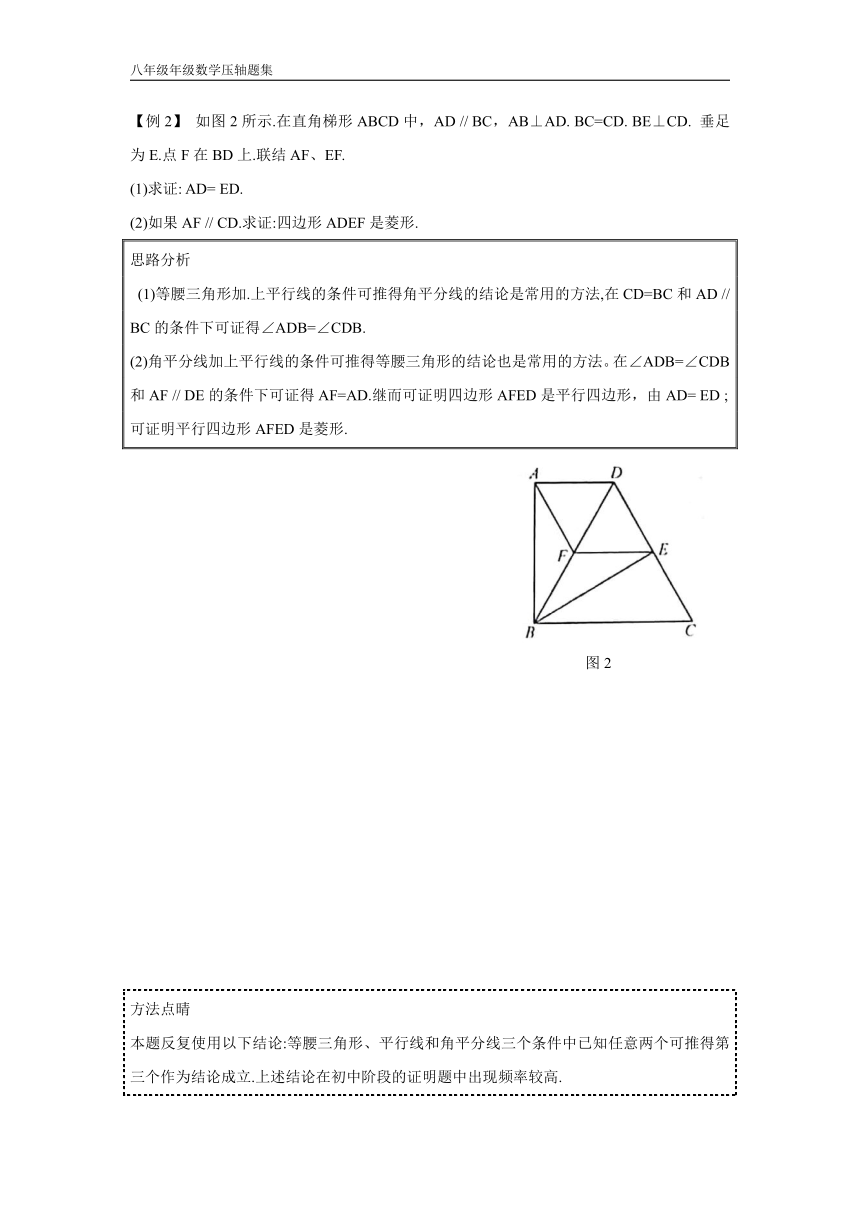
【例2】
如图2所示.在直角梯形ABCD中,AD
//
BC,AB⊥AD.
BC=CD.
BE⊥CD.
垂足为E.点F在BD上.联结AF、EF.
(1)求证:
AD=
ED.
(2)如果AF
//
CD.求证:四边形ADEF是菱形.
思路分析
(1)等腰三角形加.上平行线的条件可推得角平分线的结论是常用的方法,在CD=BC和AD
//
BC的条件下可证得∠ADB=∠CDB.
(2)角平分线加上平行线的条件可推得等腰三角形的结论也是常用的方法。在∠ADB=∠CDB和AF
//
DE的条件下可证得AF=AD.继而可证明四边形AFED是平行四边形,由AD=
ED
;
可证明平行四边形AFED是菱形.
方法点晴
本题反复使用以下结论:等腰三角形、平行线和角平分线三个条件中已知任意两个可推得第三个作为结论成立.上述结论在初中阶段的证明题中出现频率较高.
【例3】
如图3所示,在△ABC和△EDC中,AC=CE=CB
=CD.∠ACB
=∠ECD=90°,
AB与CE交于点F,ED与AB、BC分别交于点M、H.
(1)求证:
CF
=CH.
(2)如图4所示,△ABC不动,将△EDC绕点C旋转到∠BCE
=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.
思路分析
(1)∠ACB=∠ECD=90°
.减去一个公共角∠BCE,得∠ACF
=∠DCH,∠A
=∠D=45°,AC=DC.可证明△ACF≌△DCH.
(2)当旋转角是45°时,旋转角∠ACE
=∠BCD
=45°,等腰Rt△ACB和等腰Rt△ECD的底角都是45°,可证DE
//
AC,
AB
//
CD,所以四边形ACDM是平行四边形,加上AC=CD的条件,可证得四边形ACDM是菱形.
图3
图4
方法点睛
证明菱形的方法一般先证明它是平行四边形,再证明邻边相等.
【星级训练】
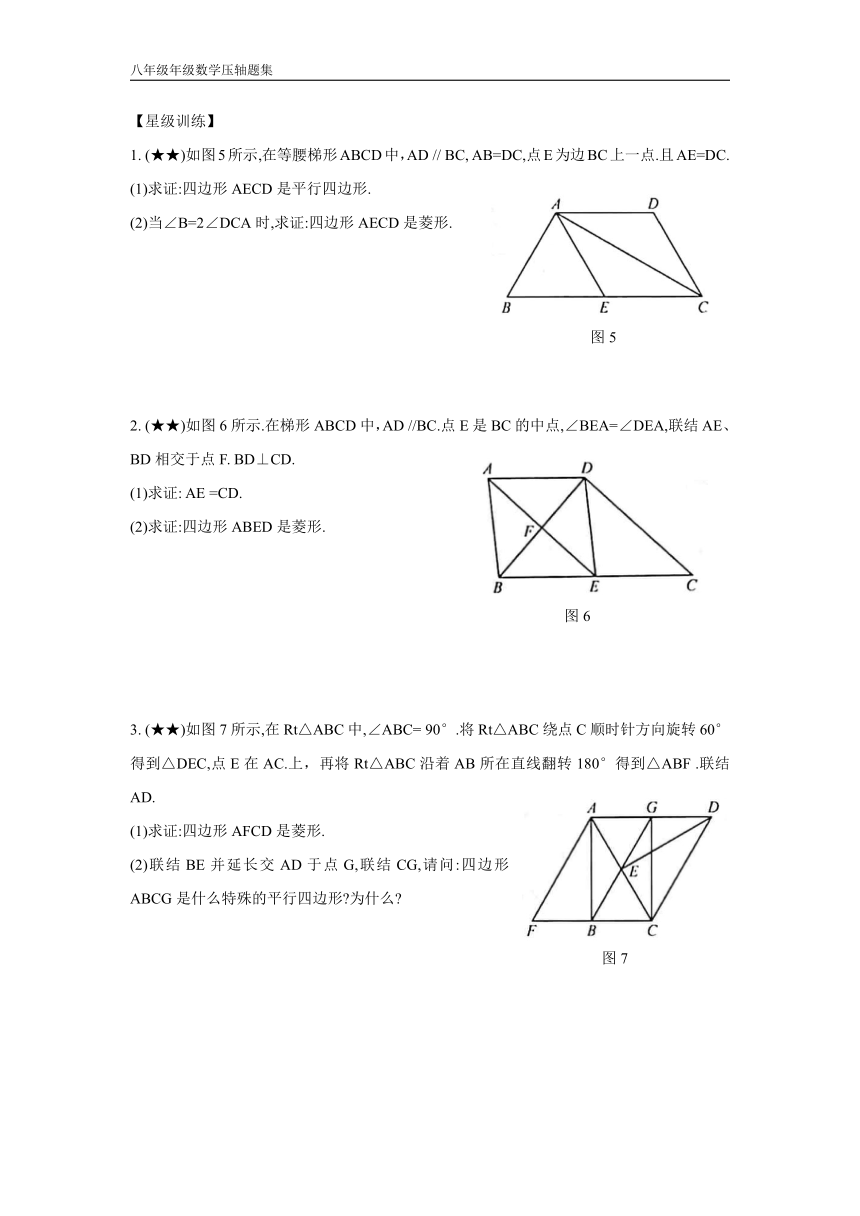
1.
(★★)如图5所示,在等腰梯形ABCD中,AD
//
BC,
AB=DC,点E为边BC上一点.且AE=DC.
(1)求证:四边形AECD是平行四边形.
(2)当∠B=2∠DCA时,求证:四边形AECD是菱形.
2.
(★★)如图6所示.在梯形ABCD中,AD
//BC.点E是BC的中点,∠BEA=∠DEA,联结AE、BD相交于点F.
BD⊥CD.
(1)求证:
AE
=CD.
(2)求证:四边形ABED是菱形.
3.
(★★)如图7所示,在Rt△ABC中,∠ABC=
90°.将Rt△ABC绕点C顺时针方向旋转60°得到△DEC,点E在AC.上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF
.联结AD.
(1)求证:四边形AFCD是菱形.
(2)联结BE并延长交AD于点G,联结CG,请问:四边形ABCG是什么特殊的平行四边形?为什么?
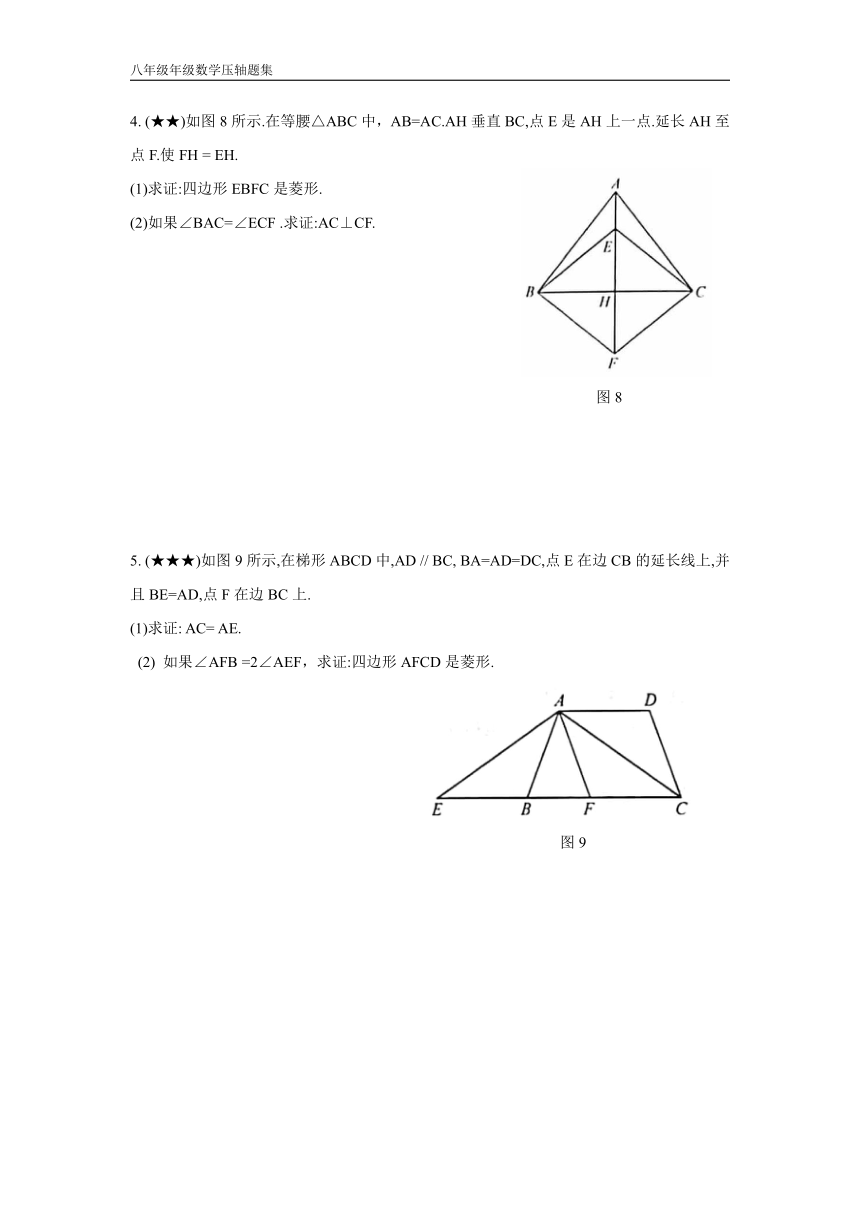
4.
(★★)如图8所示.在等腰△ABC中,AB=AC.AH垂直BC,点E是AH上一点.延长AH至点F.使FH
=
EH.
(1)求证:四边形EBFC是菱形.
(2)如果∠BAC=∠ECF
.求证:AC⊥CF.
5.
(★★★)如图9所示,在梯形ABCD中,AD
//
BC,
BA=AD=DC,点E在边CB的延长线上,并且BE=AD,点F在边BC上.
(1)求证:
AC=
AE.
(2)
如果∠AFB
=2∠AEF,求证:四边形AFCD是菱形.
2、正方形
【要点导航】
正方形是初中平面几何的一个重要内容.也是中考必考内容之一.正方形作为特殊的矩形和菱形关于边、角、对角线的性质丰富.有三种判定方法.若已知条件出现在四边形的边上,则应考虑:有一组邻边相等的矩形是正方形:有一组邻边相等且有一个角是直角的平行四边形是正方形.若已知条件出现在四边形的角上.则应考虑:有一个角为直角的菱形是正方形。
【典型例题】
【例1】
如图10所示,已知在△ABC中,AB=AC.
AD是∠BAC的平分线.交BC于点D.
AN是△ABC外角∠CAM的平分线.CE⊥AN.垂足为E.
(1)求证:四边形ADCE是矩形.
(2)
当△ABC满足什么条件时,四边形ADCE是一个正方形?请加以证明.
思路分析
(1)
AN和AD分别是邻补角∠BAC和∠MAC的平分线.所以AN和AD的夹角为90°.加上∠AEC和∠ADC两个直角。可证明四边形ADCE是矩形.
(2)当四边形ADCE是一个正方形时,∠DAC=45°.所以△ADC是等腰直角三角形。
可得△ABC是等腰直角三角形.
方法点睛
第(2)小题先由四边形ADCE是正方形作为条件探索出∠1
=45°
.继而得到△ABC是等腰直角三角形,再由△ABC是等腰直角三角形作为条件来证明四边形ADCE是正方形
【例2】如图11所示.在平行四边形ABCD中,对角线AC、BD交于点O,点E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED
=2∠EAD,求证:四边形ABCD是正方形.
思路分析
(1)
△ACE是等边三角形,所以AE=
EC,加上AO=CO的条件可得EO.
l
AC.即对角线互相垂直.
(2)由∠AED=
2∠EAD.可设∠EAD=
x,∠AED=
2x,则外角∠ADO
=∠EAD+∠AED=3x.等边三角形的内角为60°,可求得x=15°.所以∠ADO=45°,可求得∠ADC
=
90°.
方法点晴
第(2)小题可求出角度的角很多,全等的三角形也有多对.根据∠AED和∠EAD的
2倍关系.分别用同一个未知数表示这两个角,利用已知条件建立方程,避免循环论证。
【例3】在正方形
ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时,如图12所示,易证BM+DN=MN.
(1)当∠MAN绕点A旋转到BM≠DN时,如图13所示,线段BM、DN和MN之间有怎样的数量关系?写出猜想.并加以证明.
(2)当∠MAN绕点A旋转到如图14所示的位置时.线段BM、DN和MN之间又有怎样的数量关系?请写出你的猜想.并证明.
思路分析
(1)∠MAN绕点A顺时针旋转过程中线段DN、BM、MN的长度都发生改变,借助正方形是旋转对称图形可将DN.
BM联结在一起,将△ADN绕着点A顺时针旋转90°,利用旋转三角形全等的条件再证明一次全等三角形即可得到结论.
(2)
当点M在CB的延长线上时,先构造一对绕着点A旋转90°重合的全等三角形,截取DE.使得DE=
BM.再利用旋转三角形全等的条件再证明一次全等三角形即可得到结论.
图12
图13
图14
方法点睛
两种证明方法统称为截长补短法.当需要证明几段较短的线段之和等于较长线段时,可以考虑将一条较短线段“补短”或者将一条较长线段“截长”。
【星级训练】
1.
(★)如图15所示,在正方形ABCD中,点E是AD边上一点,且BE=CE,
BE与对角线AC交于点F.联结DF.交EC于点G.求证:
(1)∠ABF
=∠ADF.
(2)
DF⊥EC.
2.
(★★)如图16所示在正方形ABCD中,点P、Q分别在CD、BC上.且∠l
=∠2.
求证:AQ
=QB+
PD.
3.
(★★)如图17所示.正方形ABCD的对角线AC、BD相交于点O.
(1)如图17(a)所示.点E为AC上一点.AG⊥EB交EB于点G.
AG交BD于点F.求证:
OE
=OF.
(2)在(1)中.若点E为AC延长线上一点.如图17(b)所示.AG⊥EB交EB的延长线于点G.
AG、BD的延长线交于点F
.其他条件不变.则结论“OE
=OF"还成立吗?若成立.请给予证明;若不成立.请说明理由.
4.
(★★)如图18所示,在△ABC中,点O为AC边上的一个动点,过点O作直线MN
//
BC.设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于点E.
(1)求证:
EO=
FO.
(2)当点O运动到何处时.四边形AECF是矩形?并证明你的结论.
(3)若AC边上存在点O.使四边形AECF是正方形,猜想△ABC的形状并证明你的
结论.
5.
(★★★)如图19所示.正方形ABCD的边长为1.点G为CD边上的一个动点(点G与点C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF
.联结DE交BG的延长线于点H.
(1)求证:△BCG≌△DCE.
(2)求证:
BH⊥DE.
(3)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由。.
6.
(★★★)如图20所示,正方形ABCD的边长为4,点E在边AB上(点E与点A、B不重合).过点A作AF⊥DE.垂足为G,
AF与边BC相交于点F.
(1)求证:
AF
=
DE.
(2)联结DF、EF.设AE=x.△DEF的面积为y,用含x的代数式表示y
(3)如果△DEF的面积为.求FG的长.
第四讲
菱形与正方形
1、菱形
【要点导航】
菱形是初中平面几何的一个重要内容.也是中考必考内容之--.菱形作为特殊的平行四边形关于边、角、对角线的性质丰富.有三种判定方法.这三种判定方法可划分为两类:一类与四边形的边有关:另一类与四边形的对角线有关.若已知条件出现在四边形的边上.则应考虑:一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形.若已知条件出现在四边形的对角线上.则应考虑:对角线垂直的平行四边形是菱形.
【典型例题】
【例1】
如图1所示.EF是矩形ABCD的对角线AC的垂直平分线.EF与对角线AC及边AD、BC分别交于点O、E、F.
(1)求证:四边形AFCE是菱形.
(2)如果FE=2ED.求AE
:
DE的值.
思路分析
(1)先证明△AOE≌OCOF
.得到对角线互相垂直平分.对角线互相平分的四边形是平行四边形,对角线互相垂.直的平行四边形是菱形.
(2)由第(1)小题的结论易得FO=EO=
ED.所以∠2=∠3=
∠4=30°.因此,图中所有的直角三角形均为含30°角的特殊直角三角形,再利用它们三边之比,便能求得AE
:
DE的值.
方法点睛
在△ACD中,CE平分2
LACD,由角平分线定理得AC与CD的比值等于AE与ED
的比值.
【例2】
如图2所示.在直角梯形ABCD中,AD
//
BC,AB⊥AD.
BC=CD.
BE⊥CD.
垂足为E.点F在BD上.联结AF、EF.
(1)求证:
AD=
ED.
(2)如果AF
//
CD.求证:四边形ADEF是菱形.
思路分析
(1)等腰三角形加.上平行线的条件可推得角平分线的结论是常用的方法,在CD=BC和AD
//
BC的条件下可证得∠ADB=∠CDB.
(2)角平分线加上平行线的条件可推得等腰三角形的结论也是常用的方法。在∠ADB=∠CDB和AF
//
DE的条件下可证得AF=AD.继而可证明四边形AFED是平行四边形,由AD=
ED
;
可证明平行四边形AFED是菱形.
方法点晴
本题反复使用以下结论:等腰三角形、平行线和角平分线三个条件中已知任意两个可推得第三个作为结论成立.上述结论在初中阶段的证明题中出现频率较高.
【例3】
如图3所示,在△ABC和△EDC中,AC=CE=CB
=CD.∠ACB
=∠ECD=90°,
AB与CE交于点F,ED与AB、BC分别交于点M、H.
(1)求证:
CF
=CH.
(2)如图4所示,△ABC不动,将△EDC绕点C旋转到∠BCE
=45°时,试判断四边形ACDM是什么四边形?并证明你的结论.
思路分析
(1)∠ACB=∠ECD=90°
.减去一个公共角∠BCE,得∠ACF
=∠DCH,∠A
=∠D=45°,AC=DC.可证明△ACF≌△DCH.
(2)当旋转角是45°时,旋转角∠ACE
=∠BCD
=45°,等腰Rt△ACB和等腰Rt△ECD的底角都是45°,可证DE
//
AC,
AB
//
CD,所以四边形ACDM是平行四边形,加上AC=CD的条件,可证得四边形ACDM是菱形.
图3
图4
方法点睛
证明菱形的方法一般先证明它是平行四边形,再证明邻边相等.
【星级训练】
1.
(★★)如图5所示,在等腰梯形ABCD中,AD
//
BC,
AB=DC,点E为边BC上一点.且AE=DC.
(1)求证:四边形AECD是平行四边形.
(2)当∠B=2∠DCA时,求证:四边形AECD是菱形.
2.
(★★)如图6所示.在梯形ABCD中,AD
//BC.点E是BC的中点,∠BEA=∠DEA,联结AE、BD相交于点F.
BD⊥CD.
(1)求证:
AE
=CD.
(2)求证:四边形ABED是菱形.
3.
(★★)如图7所示,在Rt△ABC中,∠ABC=
90°.将Rt△ABC绕点C顺时针方向旋转60°得到△DEC,点E在AC.上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF
.联结AD.
(1)求证:四边形AFCD是菱形.
(2)联结BE并延长交AD于点G,联结CG,请问:四边形ABCG是什么特殊的平行四边形?为什么?
4.
(★★)如图8所示.在等腰△ABC中,AB=AC.AH垂直BC,点E是AH上一点.延长AH至点F.使FH
=
EH.
(1)求证:四边形EBFC是菱形.
(2)如果∠BAC=∠ECF
.求证:AC⊥CF.
5.
(★★★)如图9所示,在梯形ABCD中,AD
//
BC,
BA=AD=DC,点E在边CB的延长线上,并且BE=AD,点F在边BC上.
(1)求证:
AC=
AE.
(2)
如果∠AFB
=2∠AEF,求证:四边形AFCD是菱形.
2、正方形
【要点导航】
正方形是初中平面几何的一个重要内容.也是中考必考内容之一.正方形作为特殊的矩形和菱形关于边、角、对角线的性质丰富.有三种判定方法.若已知条件出现在四边形的边上,则应考虑:有一组邻边相等的矩形是正方形:有一组邻边相等且有一个角是直角的平行四边形是正方形.若已知条件出现在四边形的角上.则应考虑:有一个角为直角的菱形是正方形。
【典型例题】
【例1】
如图10所示,已知在△ABC中,AB=AC.
AD是∠BAC的平分线.交BC于点D.
AN是△ABC外角∠CAM的平分线.CE⊥AN.垂足为E.
(1)求证:四边形ADCE是矩形.
(2)
当△ABC满足什么条件时,四边形ADCE是一个正方形?请加以证明.
思路分析
(1)
AN和AD分别是邻补角∠BAC和∠MAC的平分线.所以AN和AD的夹角为90°.加上∠AEC和∠ADC两个直角。可证明四边形ADCE是矩形.
(2)当四边形ADCE是一个正方形时,∠DAC=45°.所以△ADC是等腰直角三角形。
可得△ABC是等腰直角三角形.
方法点睛
第(2)小题先由四边形ADCE是正方形作为条件探索出∠1
=45°
.继而得到△ABC是等腰直角三角形,再由△ABC是等腰直角三角形作为条件来证明四边形ADCE是正方形
【例2】如图11所示.在平行四边形ABCD中,对角线AC、BD交于点O,点E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED
=2∠EAD,求证:四边形ABCD是正方形.
思路分析
(1)
△ACE是等边三角形,所以AE=
EC,加上AO=CO的条件可得EO.
l
AC.即对角线互相垂直.
(2)由∠AED=
2∠EAD.可设∠EAD=
x,∠AED=
2x,则外角∠ADO
=∠EAD+∠AED=3x.等边三角形的内角为60°,可求得x=15°.所以∠ADO=45°,可求得∠ADC
=
90°.
方法点晴
第(2)小题可求出角度的角很多,全等的三角形也有多对.根据∠AED和∠EAD的
2倍关系.分别用同一个未知数表示这两个角,利用已知条件建立方程,避免循环论证。
【例3】在正方形
ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.当∠MAN绕点A旋转到BM=DN时,如图12所示,易证BM+DN=MN.
(1)当∠MAN绕点A旋转到BM≠DN时,如图13所示,线段BM、DN和MN之间有怎样的数量关系?写出猜想.并加以证明.
(2)当∠MAN绕点A旋转到如图14所示的位置时.线段BM、DN和MN之间又有怎样的数量关系?请写出你的猜想.并证明.
思路分析
(1)∠MAN绕点A顺时针旋转过程中线段DN、BM、MN的长度都发生改变,借助正方形是旋转对称图形可将DN.
BM联结在一起,将△ADN绕着点A顺时针旋转90°,利用旋转三角形全等的条件再证明一次全等三角形即可得到结论.
(2)
当点M在CB的延长线上时,先构造一对绕着点A旋转90°重合的全等三角形,截取DE.使得DE=
BM.再利用旋转三角形全等的条件再证明一次全等三角形即可得到结论.
图12
图13
图14
方法点睛
两种证明方法统称为截长补短法.当需要证明几段较短的线段之和等于较长线段时,可以考虑将一条较短线段“补短”或者将一条较长线段“截长”。
【星级训练】
1.
(★)如图15所示,在正方形ABCD中,点E是AD边上一点,且BE=CE,
BE与对角线AC交于点F.联结DF.交EC于点G.求证:
(1)∠ABF
=∠ADF.
(2)
DF⊥EC.
2.
(★★)如图16所示在正方形ABCD中,点P、Q分别在CD、BC上.且∠l
=∠2.
求证:AQ
=QB+
PD.
3.
(★★)如图17所示.正方形ABCD的对角线AC、BD相交于点O.
(1)如图17(a)所示.点E为AC上一点.AG⊥EB交EB于点G.
AG交BD于点F.求证:
OE
=OF.
(2)在(1)中.若点E为AC延长线上一点.如图17(b)所示.AG⊥EB交EB的延长线于点G.
AG、BD的延长线交于点F
.其他条件不变.则结论“OE
=OF"还成立吗?若成立.请给予证明;若不成立.请说明理由.
4.
(★★)如图18所示,在△ABC中,点O为AC边上的一个动点,过点O作直线MN
//
BC.设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于点E.
(1)求证:
EO=
FO.
(2)当点O运动到何处时.四边形AECF是矩形?并证明你的结论.
(3)若AC边上存在点O.使四边形AECF是正方形,猜想△ABC的形状并证明你的
结论.
5.
(★★★)如图19所示.正方形ABCD的边长为1.点G为CD边上的一个动点(点G与点C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF
.联结DE交BG的延长线于点H.
(1)求证:△BCG≌△DCE.
(2)求证:
BH⊥DE.
(3)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由。.
6.
(★★★)如图20所示,正方形ABCD的边长为4,点E在边AB上(点E与点A、B不重合).过点A作AF⊥DE.垂足为G,
AF与边BC相交于点F.
(1)求证:
AF
=
DE.
(2)联结DF、EF.设AE=x.△DEF的面积为y,用含x的代数式表示y
(3)如果△DEF的面积为.求FG的长.
