高中数学:2.1离散型随机变量的分布列学案Word含解析
文档属性
| 名称 | 高中数学:2.1离散型随机变量的分布列学案Word含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 252.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 21:52:24 | ||
图片预览




文档简介
2.1.2 离散型随机变量的分布列
[目标]
1.能知道取有限个值的离散型随机变量及其分布列的概念.2.会求出简单的离散型随机变量的分布列并能记住分布列的性质.3.能知道两点分布和超几何分布及其导出过程,并能简单的运用.
[重点]
1.理解取有限个值的离散型随机变量及其分布列的概念与性质.2.会求简单的离散型随机变量的分布列.
[难点]
两点分布和超几何分布.
知识点一
离散型随机变量的分布列
[填一填]
(1)所有取值可以一一列出的随机变量,称为离散型随机变量.
(2)离散型随机变量X可能的取值为x1,x2,…,xi,…,xn,则它的概率分布列用表格可表示为
X
x1
x2
…
xn
P
p1
p2
…
pn
用等式可表示为P(X=xi)=pi,i=1,2,…,n,离散型随机变量分布列的变化情况可以用图象来表示.
[答一答]
1.表格中的x1,x2,…,xn及p1,p2,…,pn分别表示什么含义?X取值为x1,x2,…,xn时所对应的事件是否互斥?
提示:表格中x1,x2,…,xn表示离散型随机变量X可能取的不同值,p1,p2,…,pn表示X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi.由随机变量的概念知随机变量X取值x1,x2,…,xn是不能同时发生的,故随机变量X取值为x1,x2,…,xn时所对应事件是互斥的.
2.表格中p1,p2,…,pn的取值范围分别是多少?
提示:由概率的意义知p1,p2,…,pn的取值范围为[0,1],即0≤pi≤1,i=1,2,…,n.
3.如何用表格的形式表示离散型随机变量的分布列?
提示:若要用表格的形式表示离散型随机变量的分布列,首先需确定X的取值,注意不要遗漏,再计算X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi,最后用表格的方法表示随机变量的分布列.
知识点二
两个特殊分布
[填一填]
1.两点分布
随机变量X的分布列是:
X
1
0
P
p
q
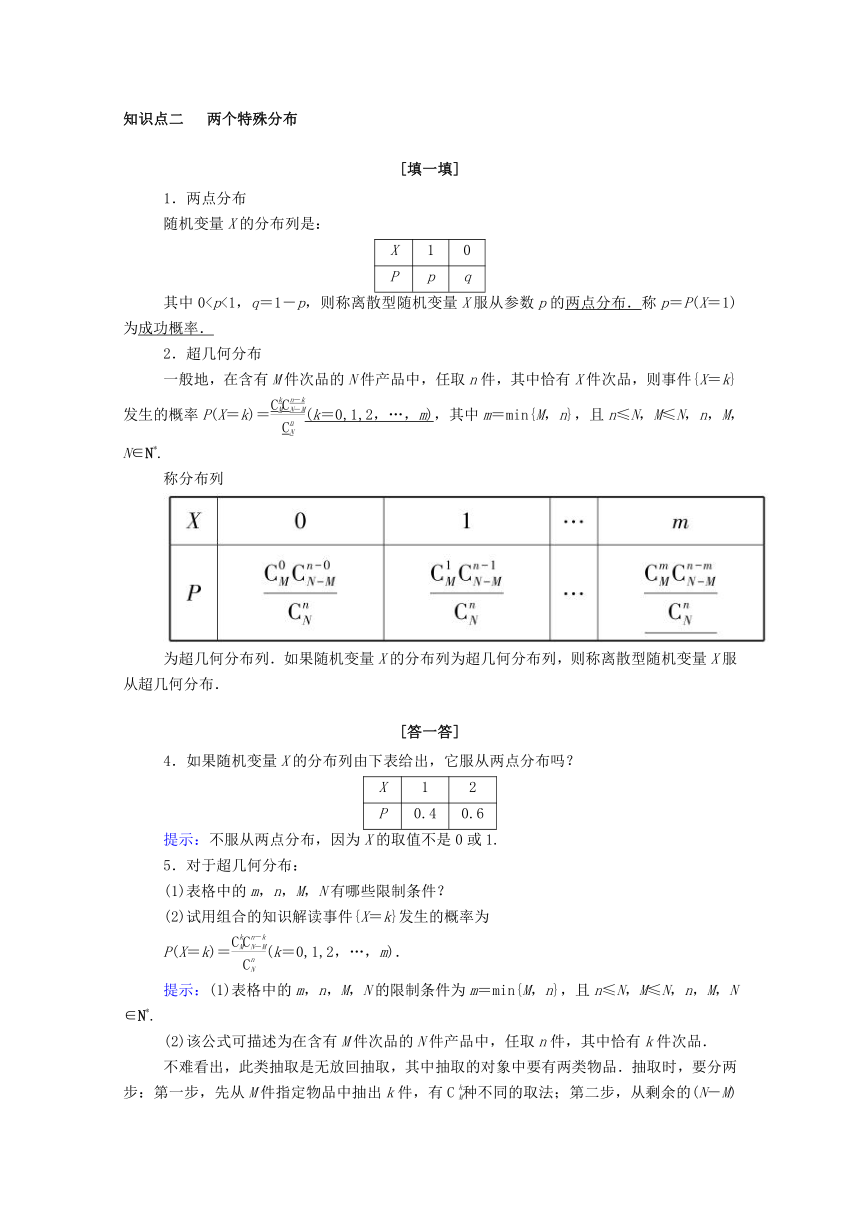
其中02.超几何分布
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则事件{X=k}发生的概率P(X=k)=(k=0,1,2,…,m),其中m=min{M,n},且n≤N,M≤N,n,M,N∈N
.
称分布列
为超几何分布列.如果随机变量X的分布列为超几何分布列,则称离散型随机变量X服从超几何分布.
[答一答]
4.如果随机变量X的分布列由下表给出,它服从两点分布吗?
X
1
2
P
0.4
0.6
提示:不服从两点分布,因为X的取值不是0或1.
5.对于超几何分布:
(1)表格中的m,n,M,N有哪些限制条件?
(2)试用组合的知识解读事件{X=k}发生的概率为
P(X=k)=(k=0,1,2,…,m).
提示:(1)表格中的m,n,M,N的限制条件为m=min{M,n},且n≤N,M≤N,n,M,N∈N
.
(2)该公式可描述为在含有M件次品的N件产品中,任取n件,其中恰有k件次品.
不难看出,此类抽取是无放回抽取,其中抽取的对象中要有两类物品.抽取时,要分两步:第一步,先从M件指定物品中抽出k件,有C种不同的取法;第二步,从剩余的(N-M)件非指定物品中,抽取(n-k)件非指定物品,有C种不同的取法.而从N件物品中抽取n件,不同的取法种数为C,所以P(X=k)=(k=0,1,2,…,m).
1.对离散型随机变量分布列的说明
(1)离散型随机变量的分布列不仅能清楚地反映其所取的一切可能的值,而且也能看出取每一个值的概率的大小,从而反映出随机变量在随机试验中取值的分布情况,是进一步研究随机试验数量特征的基础.
(2)离散型随机变量在某一范围内取值的概率等于它取这个范围内各值的概率之和.
(3)离散型随机变量可以用分布列、解析式、图象表示.
2.超几何分布的理解
(1)超几何分布的模型是不放回抽样.
(2)超几何分布中的参数是M,N,n.
(3)超几何分布可解决产品中的正品和次品、盒中的白球和黑球、同学中的男和女等问题,往往由差异明显的两部分组成.
类型一
求离散型随机变量的分布列
【例1】 从装有除颜色外完全相同的6个白球,4个黑球和2个黄球的箱中随机地取出两个球,规定每取出1个黑球赢2元,而每取出1个白球输1元,取出黄球无输赢.
(1)以X表示赢得的钱数,随机变量X可以取哪些值?求X的分布列;
(2)求出赢钱(即X>0时)的概率.
【解】 (1)从箱中取两个球的情形有以下6种:{2个白球},{1个白球,1个黄球},{1个白球,1个黑球},{2个黄球},{1个黑球,1个黄球},{2个黑球}.
当取到2个白球时,随机变量X=-2;
当取到1个白球,1个黄球时,随机变量X=-1;
当取到1个白球,1个黑球时,随机变量X=1;
当取到2个黄球时,随机变量X=0;
当取到1个黑球,1个黄球时,随机变量X=2;
当取到2个黑球时,随机变量X=4.
所以随机变量X的可能取值为-2,-1,0,1,2,4.
P(X=-2)==,
P(X=-1)==,
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=4)==.
所以X的分布列如下:
X
-2
-1
0
1
2
4
P
(2)P(X>0)=P(X=1)+P(X=2)+P(X=4)=++=.
所以赢钱的概率为.
解题的关键有两点:一是依据试验的所有可能结果写出随机变量的可能取值;二是依据随机变量取值所对应的结果求出随机变量取每一个值的概率.另外,利用随机变量分布列中各个概率和为1对所求分布列进行验证也会防止出错.
练习:
一袋中装有4只同样大小的球,编号分别为1,2,3,4,现从中随机取出2个球,以X表示取出球的最大号码,则X的分布列为
X
2
3
4
P
.
解析:由题意随机变量X所有可能取值为2,3,4.
且P(X=2)==,P(X=3)==,P(X=4)==.
因此X的分布列为
X
2
3
4
P
类型二
分布列的性质
【例2】 已知离散型随机变量ξ的分布列为P
=ak(k=1,2,3,4,5).
(1)求常数a的值;
(2)求P;
(3)求P.
【解】 由题意知离散型随机变量ξ的分布列为
ξ
P
a
2a
3a
4a
5a
(1)a+2a+3a+4a+5a=1,得a=;
(2)方法1:P=P+P+P=++=.
方法2:P=1-P=1-=;
(3)因为<ξ<,所以ξ所有可能的取值为,,,故P=P+P+P
=++=.
本题是一道离散型随机变量的分布列的计算与离散型随机变量的分布列的性质的应用综合起来的好题.主要先由离散型随机变量的分布列的性质求出a的值,然后写出其相应的离散型随机变量的分布列,再利用离散型随机变量的分布列求出其相应的概率.本题中离散型随机变量取不同的值时所表示的随机事件彼此互斥,故由概率的加法公式求出其概率.
练习:
已知离散型随机变量ξ的分布列如下:
ξ
1
2
…
n
P
k
2k
…
2n-1·k
求k的值.
解:因为1=k+2k+…+2n-1k=k(1+2+…+2n-1)=k·=(2n-1)k,所以k=.
类型三
超几何分布
【例3】 某高二数学兴趣小组有7名同学,其中有4名同学参加过高一数学“南方杯”竞赛.若从该小组中任选3名同学参加高二数学“南方杯”竞赛,求这3名同学中参加过高一数学“南方杯”竞赛的人数ξ的分布列及P(ξ<2).
【分析】 该问题与抽取产品在本质上是一致的,从而可用超几何分布解决.
【解】 由题意可知,ξ的可能取值为0,1,2,3,则
P(ξ=0)==,
P(ξ=1)==,
P(ξ=2)==,
P(ξ=3)==.
所以,随机变量ξ的分布列为
ξ
0
1
2
3
P
P(ξ<2)=P(ξ=0)+P(ξ=1)=+=.
求超几何分布的分布列,关键是求得P?X=m?的值,而求值就要先明确N,M和n的值分别是什么.注意有放回地抽样不是超几何分布,不能用这种方法计算.
练习:
袋中有4个红球,3个黑球,从袋中随机取4个球,设取到一个红球得2分,取到一个黑球得1分.
(1)求得分X的分布列;
(2)求得分大于6分的概率.
解:(1)从袋中随机摸4个球的情况为:1红3黑,2红2黑,3红1黑,4红四种情况,分别得分为5分,6分,7分,8分,故X的可能取值为5,6,7,8.
P(X=5)==,
P(X=6)==,
P(X=7)==,
P(X=8)==.
故所求分布列为
X
5
6
7
8
P
(2)根据随机变量X的分布列,可以得到得分大于6分的概率为:P(X>6)=P(X=7)+P(X=8)=+=.
分布列与统计知识的综合应用
【例4】 经销商经销某种农产品,在一个销售季度内,每售出1
t该产品获利润500元,未售出的产品,每1
t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130
t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57
000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的分布列.
【思路分析】 每一个小矩形的面积即相应的概率.
【解】 (1)当X∈[100,130)时,T=500X-300(130-X)=800X-39
000,
当X∈[130,150]时,T=500×130=65
000.
所以T=
(2)由(1)知利润T不少于57
000元时120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57
000元的概率的估计值为0.7.
(3)依题意可得T的分布列为
T
45
000
53
000
61
000
65
000
P
0.1
0.2
0.3
0.4
【解后反思】 离散型随机变量的分布列与统计知识的综合考查是高考考查学生能力的一个重要体现.
练习:
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.
(1)根据频率分布直方图,求重量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列.
解:(1)根据频率分布直方图可知,重量超过505克的产品数量为40×(0.05×5+0.01×5)=40×0.3=12.
(2)Y的可能取值为0,1,2,且Y服从参数为N=40,M=12,n=2的超几何分布,故P(Y=0)==,P(Y=1)==,P(Y=2)==.
所以Y的分布列为
Y
0
1
2
P
1.下列给出的有可能是某个随机变量的分布列的是( C )
解析:要构成分布列,则表中第二行的值加起来应该等于1,而A、B、D明显不满足.
2.随机变量ξ的分布列为,其中a,b,c成等差数列.则P(|ξ|=1)等于( D )
A. B. C. D.
解析:∵a,b,c成等差数列,∴2b=a+c.
又∵a+b+c=1,∴b=.
∴P(|ξ|=1)=a+c=.
3.把3个骰子全部掷出,设出现6点的骰子个数是X,则P(X<2)=.
解析:P(X<2)=P(X=0)+P(X=1)
=+==.
4.已知随机变量ξ的分布列是
ξ
0
1
2
3
4
P
0.1
0.2
0.4
0.1
x
则x=0.2,P(2≤ξ≤4)=0.7.
解析:由于0.1+0.2+0.4+0.1+x=1,所以x=0.2.
P(2≤ξ≤4)=0.4+0.1+x=0.7.
5.某次歌唱比赛,需要加试文化科学素质,每位参赛选手需加答3个问题,组委会为每位选手都备有10道不同的题目可供选择,其中有5道文史类题目,3道科技类题目,2道体育类题目,测试时,每位选手从给定的10道题中不放回地随机抽取3次,每次抽取一道题,回答完该题后,再抽取下一道题目作答.
(1)求某选手第二次抽到的不是科技类题目的概率;
(2)求某选手抽到体育类题目数ξ的分布列.
解:(1)由题意可知某选手第二次抽到的不是科技类题目的概率P=+=.
(2)ξ的取值为0,1,2,
P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==.
则ξ的分布列为
ξ
0
1
2
P
PAGE
[目标]
1.能知道取有限个值的离散型随机变量及其分布列的概念.2.会求出简单的离散型随机变量的分布列并能记住分布列的性质.3.能知道两点分布和超几何分布及其导出过程,并能简单的运用.
[重点]
1.理解取有限个值的离散型随机变量及其分布列的概念与性质.2.会求简单的离散型随机变量的分布列.
[难点]
两点分布和超几何分布.
知识点一
离散型随机变量的分布列
[填一填]
(1)所有取值可以一一列出的随机变量,称为离散型随机变量.
(2)离散型随机变量X可能的取值为x1,x2,…,xi,…,xn,则它的概率分布列用表格可表示为
X
x1
x2
…
xn
P
p1
p2
…
pn
用等式可表示为P(X=xi)=pi,i=1,2,…,n,离散型随机变量分布列的变化情况可以用图象来表示.
[答一答]
1.表格中的x1,x2,…,xn及p1,p2,…,pn分别表示什么含义?X取值为x1,x2,…,xn时所对应的事件是否互斥?
提示:表格中x1,x2,…,xn表示离散型随机变量X可能取的不同值,p1,p2,…,pn表示X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi.由随机变量的概念知随机变量X取值x1,x2,…,xn是不能同时发生的,故随机变量X取值为x1,x2,…,xn时所对应事件是互斥的.
2.表格中p1,p2,…,pn的取值范围分别是多少?
提示:由概率的意义知p1,p2,…,pn的取值范围为[0,1],即0≤pi≤1,i=1,2,…,n.
3.如何用表格的形式表示离散型随机变量的分布列?
提示:若要用表格的形式表示离散型随机变量的分布列,首先需确定X的取值,注意不要遗漏,再计算X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi,最后用表格的方法表示随机变量的分布列.
知识点二
两个特殊分布
[填一填]
1.两点分布
随机变量X的分布列是:
X
1
0
P
p
q
其中0
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则事件{X=k}发生的概率P(X=k)=(k=0,1,2,…,m),其中m=min{M,n},且n≤N,M≤N,n,M,N∈N
.
称分布列
为超几何分布列.如果随机变量X的分布列为超几何分布列,则称离散型随机变量X服从超几何分布.
[答一答]
4.如果随机变量X的分布列由下表给出,它服从两点分布吗?
X
1
2
P
0.4
0.6
提示:不服从两点分布,因为X的取值不是0或1.
5.对于超几何分布:
(1)表格中的m,n,M,N有哪些限制条件?
(2)试用组合的知识解读事件{X=k}发生的概率为
P(X=k)=(k=0,1,2,…,m).
提示:(1)表格中的m,n,M,N的限制条件为m=min{M,n},且n≤N,M≤N,n,M,N∈N
.
(2)该公式可描述为在含有M件次品的N件产品中,任取n件,其中恰有k件次品.
不难看出,此类抽取是无放回抽取,其中抽取的对象中要有两类物品.抽取时,要分两步:第一步,先从M件指定物品中抽出k件,有C种不同的取法;第二步,从剩余的(N-M)件非指定物品中,抽取(n-k)件非指定物品,有C种不同的取法.而从N件物品中抽取n件,不同的取法种数为C,所以P(X=k)=(k=0,1,2,…,m).
1.对离散型随机变量分布列的说明
(1)离散型随机变量的分布列不仅能清楚地反映其所取的一切可能的值,而且也能看出取每一个值的概率的大小,从而反映出随机变量在随机试验中取值的分布情况,是进一步研究随机试验数量特征的基础.
(2)离散型随机变量在某一范围内取值的概率等于它取这个范围内各值的概率之和.
(3)离散型随机变量可以用分布列、解析式、图象表示.
2.超几何分布的理解
(1)超几何分布的模型是不放回抽样.
(2)超几何分布中的参数是M,N,n.
(3)超几何分布可解决产品中的正品和次品、盒中的白球和黑球、同学中的男和女等问题,往往由差异明显的两部分组成.
类型一
求离散型随机变量的分布列
【例1】 从装有除颜色外完全相同的6个白球,4个黑球和2个黄球的箱中随机地取出两个球,规定每取出1个黑球赢2元,而每取出1个白球输1元,取出黄球无输赢.
(1)以X表示赢得的钱数,随机变量X可以取哪些值?求X的分布列;
(2)求出赢钱(即X>0时)的概率.
【解】 (1)从箱中取两个球的情形有以下6种:{2个白球},{1个白球,1个黄球},{1个白球,1个黑球},{2个黄球},{1个黑球,1个黄球},{2个黑球}.
当取到2个白球时,随机变量X=-2;
当取到1个白球,1个黄球时,随机变量X=-1;
当取到1个白球,1个黑球时,随机变量X=1;
当取到2个黄球时,随机变量X=0;
当取到1个黑球,1个黄球时,随机变量X=2;
当取到2个黑球时,随机变量X=4.
所以随机变量X的可能取值为-2,-1,0,1,2,4.
P(X=-2)==,
P(X=-1)==,
P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=4)==.
所以X的分布列如下:
X
-2
-1
0
1
2
4
P
(2)P(X>0)=P(X=1)+P(X=2)+P(X=4)=++=.
所以赢钱的概率为.
解题的关键有两点:一是依据试验的所有可能结果写出随机变量的可能取值;二是依据随机变量取值所对应的结果求出随机变量取每一个值的概率.另外,利用随机变量分布列中各个概率和为1对所求分布列进行验证也会防止出错.
练习:
一袋中装有4只同样大小的球,编号分别为1,2,3,4,现从中随机取出2个球,以X表示取出球的最大号码,则X的分布列为
X
2
3
4
P
.
解析:由题意随机变量X所有可能取值为2,3,4.
且P(X=2)==,P(X=3)==,P(X=4)==.
因此X的分布列为
X
2
3
4
P
类型二
分布列的性质
【例2】 已知离散型随机变量ξ的分布列为P
=ak(k=1,2,3,4,5).
(1)求常数a的值;
(2)求P;
(3)求P.
【解】 由题意知离散型随机变量ξ的分布列为
ξ
P
a
2a
3a
4a
5a
(1)a+2a+3a+4a+5a=1,得a=;
(2)方法1:P=P+P+P=++=.
方法2:P=1-P=1-=;
(3)因为<ξ<,所以ξ所有可能的取值为,,,故P=P+P+P
=++=.
本题是一道离散型随机变量的分布列的计算与离散型随机变量的分布列的性质的应用综合起来的好题.主要先由离散型随机变量的分布列的性质求出a的值,然后写出其相应的离散型随机变量的分布列,再利用离散型随机变量的分布列求出其相应的概率.本题中离散型随机变量取不同的值时所表示的随机事件彼此互斥,故由概率的加法公式求出其概率.
练习:
已知离散型随机变量ξ的分布列如下:
ξ
1
2
…
n
P
k
2k
…
2n-1·k
求k的值.
解:因为1=k+2k+…+2n-1k=k(1+2+…+2n-1)=k·=(2n-1)k,所以k=.
类型三
超几何分布
【例3】 某高二数学兴趣小组有7名同学,其中有4名同学参加过高一数学“南方杯”竞赛.若从该小组中任选3名同学参加高二数学“南方杯”竞赛,求这3名同学中参加过高一数学“南方杯”竞赛的人数ξ的分布列及P(ξ<2).
【分析】 该问题与抽取产品在本质上是一致的,从而可用超几何分布解决.
【解】 由题意可知,ξ的可能取值为0,1,2,3,则
P(ξ=0)==,
P(ξ=1)==,
P(ξ=2)==,
P(ξ=3)==.
所以,随机变量ξ的分布列为
ξ
0
1
2
3
P
P(ξ<2)=P(ξ=0)+P(ξ=1)=+=.
求超几何分布的分布列,关键是求得P?X=m?的值,而求值就要先明确N,M和n的值分别是什么.注意有放回地抽样不是超几何分布,不能用这种方法计算.
练习:
袋中有4个红球,3个黑球,从袋中随机取4个球,设取到一个红球得2分,取到一个黑球得1分.
(1)求得分X的分布列;
(2)求得分大于6分的概率.
解:(1)从袋中随机摸4个球的情况为:1红3黑,2红2黑,3红1黑,4红四种情况,分别得分为5分,6分,7分,8分,故X的可能取值为5,6,7,8.
P(X=5)==,
P(X=6)==,
P(X=7)==,
P(X=8)==.
故所求分布列为
X
5
6
7
8
P
(2)根据随机变量X的分布列,可以得到得分大于6分的概率为:P(X>6)=P(X=7)+P(X=8)=+=.
分布列与统计知识的综合应用
【例4】 经销商经销某种农产品,在一个销售季度内,每售出1
t该产品获利润500元,未售出的产品,每1
t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130
t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57
000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的分布列.
【思路分析】 每一个小矩形的面积即相应的概率.
【解】 (1)当X∈[100,130)时,T=500X-300(130-X)=800X-39
000,
当X∈[130,150]时,T=500×130=65
000.
所以T=
(2)由(1)知利润T不少于57
000元时120≤X≤150.
由直方图知需求量X∈[120,150]的频率为0.7,所以下一个销售季度内的利润T不少于57
000元的概率的估计值为0.7.
(3)依题意可得T的分布列为
T
45
000
53
000
61
000
65
000
P
0.1
0.2
0.3
0.4
【解后反思】 离散型随机变量的分布列与统计知识的综合考查是高考考查学生能力的一个重要体现.
练习:
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.
(1)根据频率分布直方图,求重量超过505克的产品数量;
(2)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列.
解:(1)根据频率分布直方图可知,重量超过505克的产品数量为40×(0.05×5+0.01×5)=40×0.3=12.
(2)Y的可能取值为0,1,2,且Y服从参数为N=40,M=12,n=2的超几何分布,故P(Y=0)==,P(Y=1)==,P(Y=2)==.
所以Y的分布列为
Y
0
1
2
P
1.下列给出的有可能是某个随机变量的分布列的是( C )
解析:要构成分布列,则表中第二行的值加起来应该等于1,而A、B、D明显不满足.
2.随机变量ξ的分布列为,其中a,b,c成等差数列.则P(|ξ|=1)等于( D )
A. B. C. D.
解析:∵a,b,c成等差数列,∴2b=a+c.
又∵a+b+c=1,∴b=.
∴P(|ξ|=1)=a+c=.
3.把3个骰子全部掷出,设出现6点的骰子个数是X,则P(X<2)=.
解析:P(X<2)=P(X=0)+P(X=1)
=+==.
4.已知随机变量ξ的分布列是
ξ
0
1
2
3
4
P
0.1
0.2
0.4
0.1
x
则x=0.2,P(2≤ξ≤4)=0.7.
解析:由于0.1+0.2+0.4+0.1+x=1,所以x=0.2.
P(2≤ξ≤4)=0.4+0.1+x=0.7.
5.某次歌唱比赛,需要加试文化科学素质,每位参赛选手需加答3个问题,组委会为每位选手都备有10道不同的题目可供选择,其中有5道文史类题目,3道科技类题目,2道体育类题目,测试时,每位选手从给定的10道题中不放回地随机抽取3次,每次抽取一道题,回答完该题后,再抽取下一道题目作答.
(1)求某选手第二次抽到的不是科技类题目的概率;
(2)求某选手抽到体育类题目数ξ的分布列.
解:(1)由题意可知某选手第二次抽到的不是科技类题目的概率P=+=.
(2)ξ的取值为0,1,2,
P(ξ=0)==,P(ξ=1)==,
P(ξ=2)==.
则ξ的分布列为
ξ
0
1
2
P
PAGE
