鲁教版 七下第八章第六节三角形内角和定理同步课时训练(word版含答案)
文档属性
| 名称 | 鲁教版 七下第八章第六节三角形内角和定理同步课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 366.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览



文档简介
第八章第六节三角形内角和定理同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,点E是边上的一点,点D在的延长线上,连接,已知,则( )
A. B. C. D.
2.如图,,,若,则的度数是( )
A. B. C. D.
3.如图,在中,于点平分交于点.则的度数为( )
A. B. C. D.
4.如图,将直尺与角的三角尺叠放在一起,若,则的大小是( )
A. B. C. D.
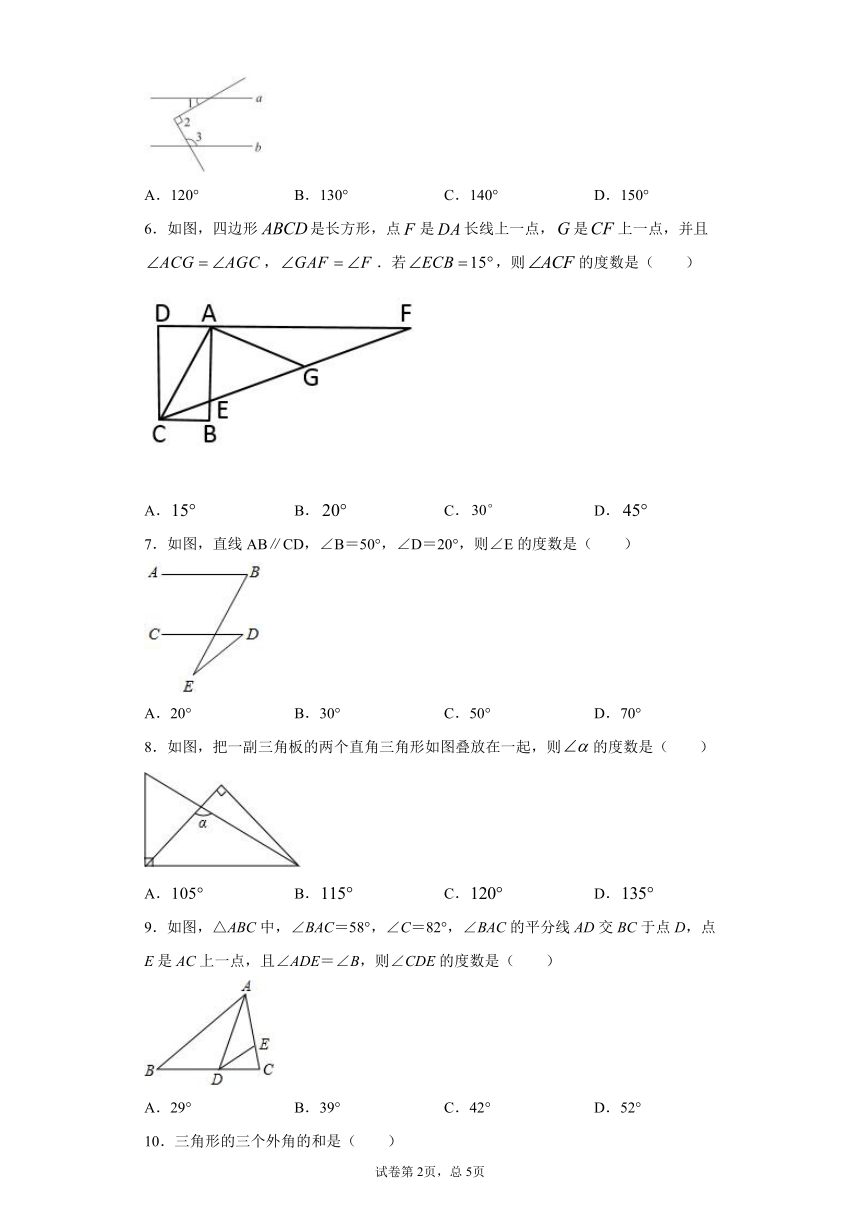
5.如图所示,直线,,,则的度数为( )
A.120° B.130° C.140° D.150°
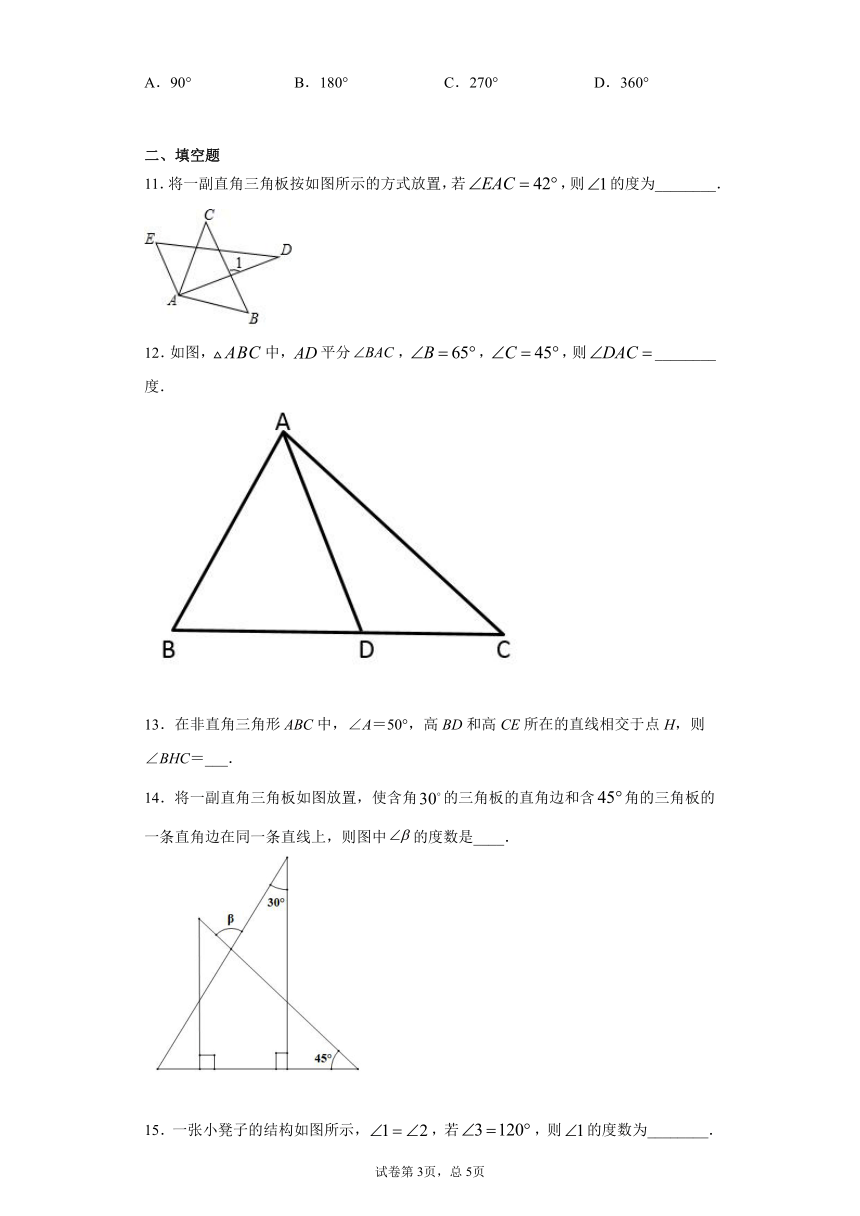
6.如图,四边形是长方形,点是长线上一点,是上一点,并且,.若,则的度数是( )
A. B. C. D.
7.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20° B.30° C.50° D.70°
8.如图,把一副三角板的两个直角三角形如图叠放在一起,则的度数是( )
A. B. C. D.
9.如图,△ABC中,∠BAC=58°,∠C=82°,∠BAC的平分线AD交BC于点D,点E是AC上一点,且∠ADE=∠B,则∠CDE的度数是( )
A.29° B.39° C.42° D.52°
10.三角形的三个外角的和是( )
A.90° B.180° C.270° D.360°
二、填空题
11.将一副直角三角板按如图所示的方式放置,若,则的度为________.
12.如图,中,平分,,,则________度.
13.在非直角三角形ABC中,∠A=50°,高BD和高CE所在的直线相交于点H,则∠BHC=___.
14.将一副直角三角板如图放置,使含角的三角板的直角边和含角的三角板的一条直角边在同一条直线上,则图中的度数是____.
15.一张小凳子的结构如图所示,,若,则的度数为________.
16.如图,在中,,,,,求的度数____________.
三、解答题
17.(1)已知直线,小亮把一块含角的直角三角尺的直角顶点放在直线上.
①若三角尺与平行线的位置如图1所示,,求的度数;
②若三角尺与平行线的位置如图2所示,且,则的度数又是多少?
(2)已知直线,小亮把一块含角的直角三角尺按图3所示放置,若,求的度数.
18.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数 .
19.如图,点B在上,与?分别交于H?G,已知,,.
(1)证明:;
(2)求的度数.
20.已知D是的边所在直线上的一点,与B,C点不重合,过D点分别作交所在直线于点F,交所在直线于点E,其中.
(1)当D在线段上时(如图),求的度数;
(2)还有没有其他情况?若有,请画出图形,并求出的度数.
参考答案
1.A
2.D
3.A
4.B
5.A
6.C
7.B
8.A
9.A
10.D
11.93°
12.35
13.50°或130°.
14.
15.60°
16.27°
17.(1)①50°;②20°;(2)35°
【详解】
解:(1)①如图①∵∠1=40°,
∴∠3=180°-∠1-90°=180°-40°-90°=50°,
∵a∥b,
∴∠2=∠3=50°;
②如图②过点B作BD∥a,
∵直线a∥b,
∴BD∥a∥b,
∴∠4=∠1=25°,
∵∠ABC=45°,
∴∠3=∠ABC-∠4=45°-25°=20°,
∴∠2=∠3=20°;
(2)如图3,∵∠3是△ADG的外角,
∴∠3=∠A+∠1=30°+25°=55°,
∵直线a∥b,
∴∠3=∠4=55°,
∵∠4+∠EFC=90°,
∴∠EFC=90°-55°=35°,
∴∠2=35°.
18.(1)∠DAE=10°;(2)∠DAE=∠C﹣∠B;(3)45°.
【详解】
解:(1)
是的高,
是的角平分线,
,
.
(2)
是的高,
是的角平分线,
,
即;
(3)和的角平分线交于点,
,即,
是的高,
,
.
故答案为:45°.
19.(1)见解析;(2)65°
【详解】
(1)证明:∵
∴
∴
∴
∵
∴
(2)解:∵且
∴
20.(1)70°;(2)有,110°
【详解】
解:(1)如图①,∵∠B+∠C=110°,
∴∠A=180°-(∠B+∠C)=70°,
∵DE∥AB,DF∥AC,
∴∠A=∠DFB,∠FDE=∠DFB,
∴∠FDE=∠A=70°;
(2)还有别的情况,
如图②,点D在射线BC上时,
∵∠B+∠ACB=110°,
∴∠BAC=180°-(∠B+∠ACB)=70°,
∵DE∥AB,DF∥AC,
∴∠BAC=∠E=70°,∠FDE+∠E=180°,
∴∠FDE=110°;
如图③,点D在射线CB上时,
∵∠ABC+∠C=110°,
∴∠BAC=180°-(∠ABC+∠C)=70°,
∵DE∥AB,DF∥AC,
∴∠BAC=∠E=70°,∠FDE+∠E=180°,
∴∠FDE=110°.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,点E是边上的一点,点D在的延长线上,连接,已知,则( )
A. B. C. D.
2.如图,,,若,则的度数是( )
A. B. C. D.
3.如图,在中,于点平分交于点.则的度数为( )
A. B. C. D.
4.如图,将直尺与角的三角尺叠放在一起,若,则的大小是( )
A. B. C. D.
5.如图所示,直线,,,则的度数为( )
A.120° B.130° C.140° D.150°
6.如图,四边形是长方形,点是长线上一点,是上一点,并且,.若,则的度数是( )
A. B. C. D.
7.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20° B.30° C.50° D.70°
8.如图,把一副三角板的两个直角三角形如图叠放在一起,则的度数是( )
A. B. C. D.
9.如图,△ABC中,∠BAC=58°,∠C=82°,∠BAC的平分线AD交BC于点D,点E是AC上一点,且∠ADE=∠B,则∠CDE的度数是( )
A.29° B.39° C.42° D.52°
10.三角形的三个外角的和是( )
A.90° B.180° C.270° D.360°
二、填空题
11.将一副直角三角板按如图所示的方式放置,若,则的度为________.
12.如图,中,平分,,,则________度.
13.在非直角三角形ABC中,∠A=50°,高BD和高CE所在的直线相交于点H,则∠BHC=___.
14.将一副直角三角板如图放置,使含角的三角板的直角边和含角的三角板的一条直角边在同一条直线上,则图中的度数是____.
15.一张小凳子的结构如图所示,,若,则的度数为________.
16.如图,在中,,,,,求的度数____________.
三、解答题
17.(1)已知直线,小亮把一块含角的直角三角尺的直角顶点放在直线上.
①若三角尺与平行线的位置如图1所示,,求的度数;
②若三角尺与平行线的位置如图2所示,且,则的度数又是多少?
(2)已知直线,小亮把一块含角的直角三角尺按图3所示放置,若,求的度数.
18.△ABC中,AD是∠BAC的角平分线,AE是△ABC的高.
(1)如图1,若∠B=40°,∠C=60°,请说明∠DAE的度数;
(2)如图2(∠B<∠C),试说明∠DAE、∠B、∠C的数量关系;
(3)如图3,延长AC到点F,∠CAE和∠BCF的角平分线交于点G,请直接写出∠G的度数 .
19.如图,点B在上,与?分别交于H?G,已知,,.
(1)证明:;
(2)求的度数.
20.已知D是的边所在直线上的一点,与B,C点不重合,过D点分别作交所在直线于点F,交所在直线于点E,其中.
(1)当D在线段上时(如图),求的度数;
(2)还有没有其他情况?若有,请画出图形,并求出的度数.
参考答案
1.A
2.D
3.A
4.B
5.A
6.C
7.B
8.A
9.A
10.D
11.93°
12.35
13.50°或130°.
14.
15.60°
16.27°
17.(1)①50°;②20°;(2)35°
【详解】
解:(1)①如图①∵∠1=40°,
∴∠3=180°-∠1-90°=180°-40°-90°=50°,
∵a∥b,
∴∠2=∠3=50°;
②如图②过点B作BD∥a,
∵直线a∥b,
∴BD∥a∥b,
∴∠4=∠1=25°,
∵∠ABC=45°,
∴∠3=∠ABC-∠4=45°-25°=20°,
∴∠2=∠3=20°;
(2)如图3,∵∠3是△ADG的外角,
∴∠3=∠A+∠1=30°+25°=55°,
∵直线a∥b,
∴∠3=∠4=55°,
∵∠4+∠EFC=90°,
∴∠EFC=90°-55°=35°,
∴∠2=35°.
18.(1)∠DAE=10°;(2)∠DAE=∠C﹣∠B;(3)45°.
【详解】
解:(1)
是的高,
是的角平分线,
,
.
(2)
是的高,
是的角平分线,
,
即;
(3)和的角平分线交于点,
,即,
是的高,
,
.
故答案为:45°.
19.(1)见解析;(2)65°
【详解】
(1)证明:∵
∴
∴
∴
∵
∴
(2)解:∵且
∴
20.(1)70°;(2)有,110°
【详解】
解:(1)如图①,∵∠B+∠C=110°,
∴∠A=180°-(∠B+∠C)=70°,
∵DE∥AB,DF∥AC,
∴∠A=∠DFB,∠FDE=∠DFB,
∴∠FDE=∠A=70°;
(2)还有别的情况,
如图②,点D在射线BC上时,
∵∠B+∠ACB=110°,
∴∠BAC=180°-(∠B+∠ACB)=70°,
∵DE∥AB,DF∥AC,
∴∠BAC=∠E=70°,∠FDE+∠E=180°,
∴∠FDE=110°;
如图③,点D在射线CB上时,
∵∠ABC+∠C=110°,
∴∠BAC=180°-(∠ABC+∠C)=70°,
∵DE∥AB,DF∥AC,
∴∠BAC=∠E=70°,∠FDE+∠E=180°,
∴∠FDE=110°.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
