鲁教版 七下第八章第四节平行线的判定定理同步课时训练(word版含答案)
文档属性
| 名称 | 鲁教版 七下第八章第四节平行线的判定定理同步课时训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 352.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览

文档简介
第八章第四节平行线的判定定理同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题中,是假命题的是( )
A.对顶角相等 B.同旁内角互补,两直线平行
C.两点之间线段最短 D.内错角相等
2.如图,在下列条件中,能判断AB∥CD的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠BAD+∠ADC=180° D.∠3=∠4
3.如图,能判断的条件是( )
A. B.
C. D.
4.下列说法中正确的个数为( )
①不相交的两条直线叫做平行线;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;
④在同一平面内,两条直线不是平行就是相交.
A.1个 B.2个 C.3个 D.4个
5.用反证法证明:“在同一个平面内,若则”时,应假设( )
A.不垂直于 B.与相交 C.不垂直于 D.都不垂直于
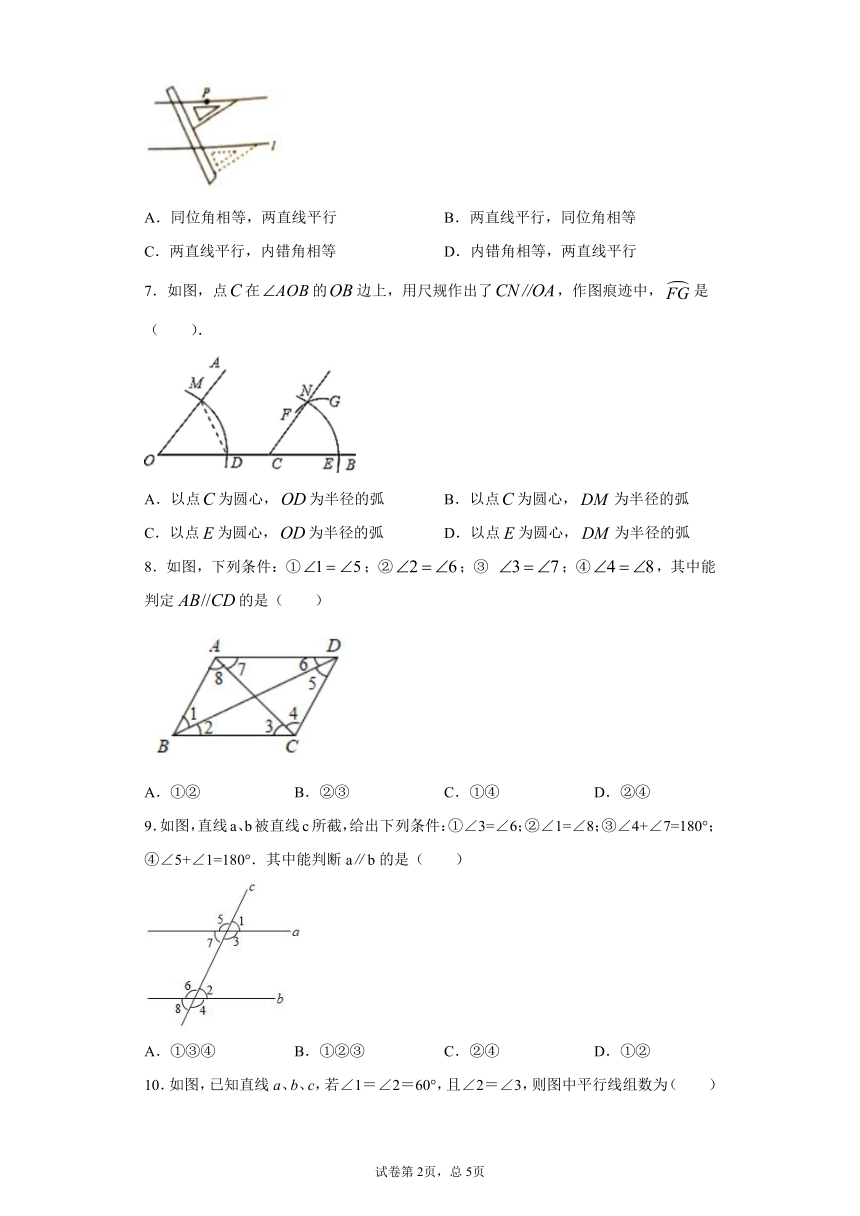
6.如图是利用直尺和三角板过直线外一点作直线的平行线的方法,这样做的依据是( )
A.同位角相等,两直线平行 B.两直线平行,同位角相等
C.两直线平行,内错角相等 D.内错角相等,两直线平行
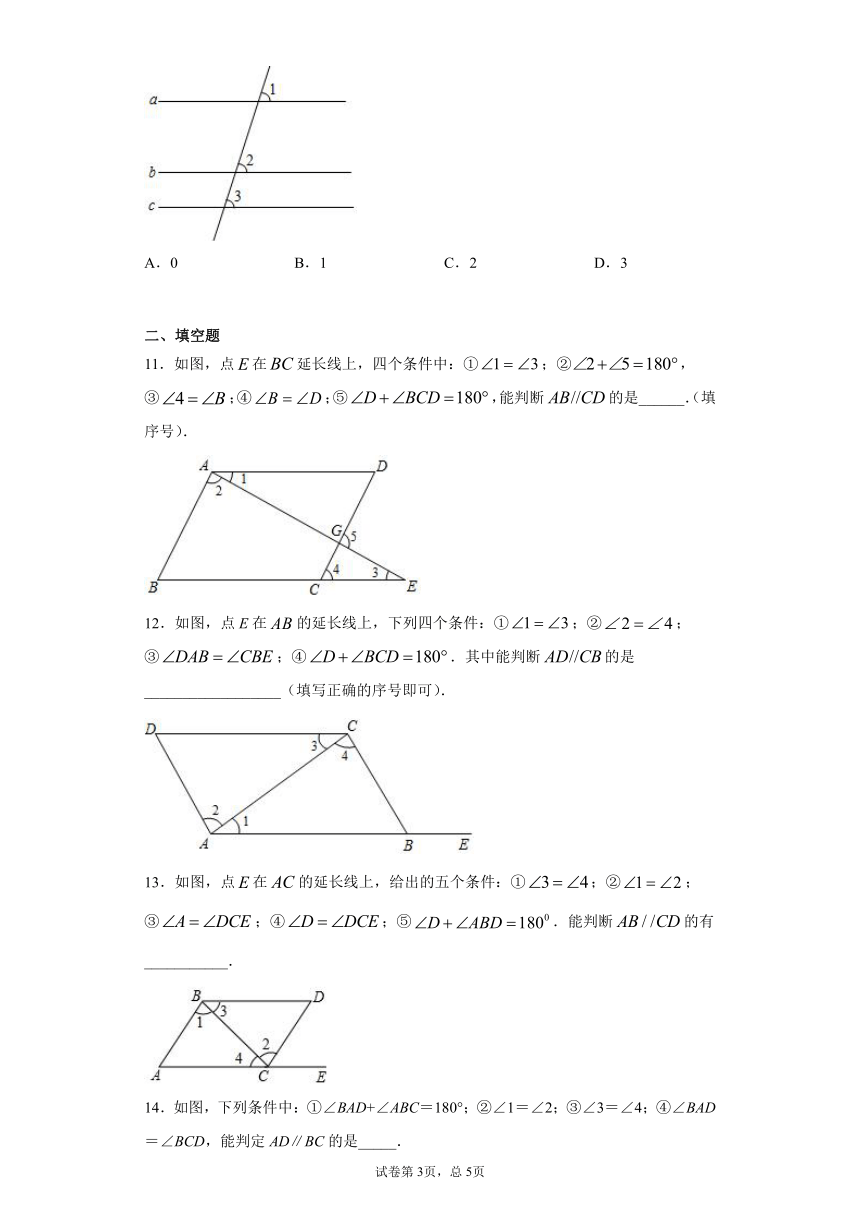
7.如图,点在的边上,用尺规作出了,作图痕迹中,是( ).
A.以点为圆心,为半径的弧 B.以点为圆心,为半径的弧
C.以点为圆心,为半径的弧 D.以点为圆心,为半径的弧
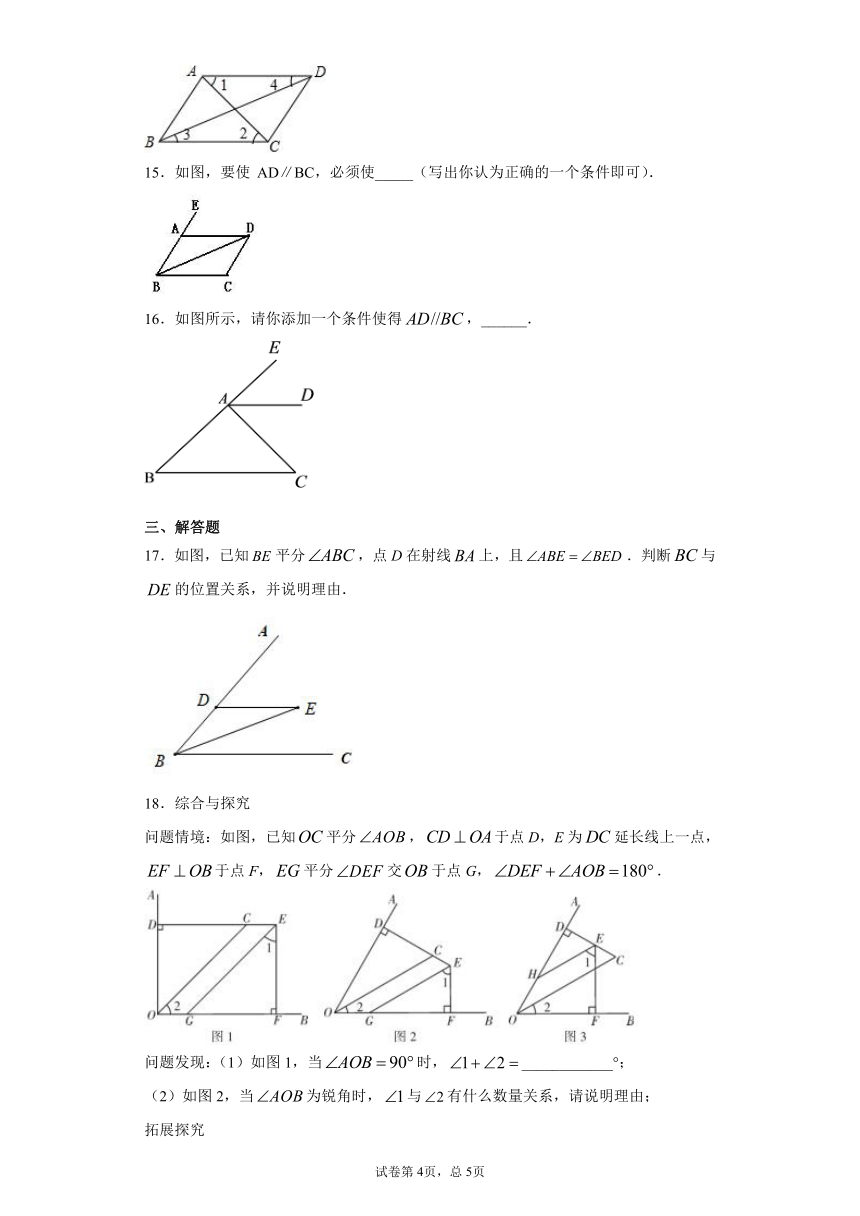
8.如图,下列条件:①;②;③ ;④,其中能判定的是( )
A.①② B.②③ C.①④ D.②④
9.如图,直线a、b被直线c所截,给出下列条件:①∠3=∠6;②∠1=∠8;③∠4+∠7=180°;④∠5+∠1=180°.其中能判断a∥b的是( )
A.①③④ B.①②③ C.②④ D.①②
10.如图,已知直线a、b、c,若∠1=∠2=60°,且∠2=∠3,则图中平行线组数为( )
A.0 B.1 C.2 D.3
二、填空题
11.如图,点在延长线上,四个条件中:①;②,③;④;⑤,能判断的是______.(填序号).
12.如图,点E在的延长线上,下列四个条件:①;②;③;④.其中能判断的是__________________(填写正确的序号即可).
13.如图,点在的延长线上,给出的五个条件:①;②;③;④;⑤.能判断的有___________.
14.如图,下列条件中:①∠BAD+∠ABC=180°;②∠1=∠2;③∠3=∠4;④∠BAD=∠BCD,能判定AD∥BC的是_____.
15.如图,要使 AD∥BC,必须使_____(写出你认为正确的一个条件即可).
16.如图所示,请你添加一个条件使得,______.
三、解答题
17.如图,已知平分,点D在射线上,且.判断与的位置关系,并说明理由.
18.综合与探究
问题情境:如图,已知平分,于点D,E为延长线上一点,于点F,平分交于点G,.
问题发现:(1)如图1,当时,____________°;
(2)如图2,当为锐角时,与有什么数量关系,请说明理由;
拓展探究
(3)在(2)的条件下,已知直角三角形中两个锐角的和是90°,试探究和的位置关系,并证明结论;
(4)如图3,当为锐角时,若点E为线段上一点,于点F,平分交于点H,.请写出一个你发现的正确结论.
19.如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
20.如图所示:
(1)若,,,求证:.
(2)若把(1)中的题设“”与结论“”对调,所得命题是否是真命题?说明理由.
参考答案
1.D
2.C
3.A
4.C
5.B
6.A
7.D
8.C
9.B
10.D
11.②③
12.②③④
13.②③⑤
14.①②③
15.∠ADB=∠CBD(答案不唯一)
16.(答案不唯一).
17.BC∥DE;理由见解析
【详解】
解:BC∥DE;理由如下:
因为平分,
所以∠ABE=∠CBE,
因为,
所以∠CBE=∠BED,
所以BC∥DE.
18.(1)90;(2),理由见解析;(3),证明见解析;(4)答案不唯一,例如
【详解】
(1)∵,
∴,
∵,
∴,
∵平分,平分,
∴∠1=∠AOB=45,∠2=∠DEF=45,
∴;
故答案为:90;
(2).
理由如下:∵,分别是,的平分线,
∴,,
∴,
∵,
∴;
(3)和的位置关系为OC∥GE.
证明:∵于点,
∴.
∴.
∵,
∴,
∴OC∥GE;
(4)答案不唯一,例如.
理由如下:∵,分别是,的平分线,
∴,,
∴,
∵,
∴;
19.AB∥EF.理由见解析.
【详解】
AB∥EF,理由如下:
∵AB∥CD,
∴∠B=∠BCD,∵∠B=70°,
∴∠BCD=70°,∵∠BCE=20°,
∴∠ECD=50°,
∵CEF=130°,
∴∠E+∠DCE=180°,
∴EF∥CD,
∴AB∥EF.
20.(1)详见解析;(2)是真命题.
【详解】
解:(1)证明:(已知),
.(两直线平行,内错角相等),
(已知),
(等量代换),
.(同位角相等,两直线平行),
.(两直线平行,同位角相等),
.(垂直的定义);
(2)是真命题,理由如下:
(已知),
,
.(同位角相等,两直线平行),
.(两直线平行,同位角相等),
(已知),
.(等量代换),
.(内错角相等,两直线平行).
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列命题中,是假命题的是( )
A.对顶角相等 B.同旁内角互补,两直线平行
C.两点之间线段最短 D.内错角相等
2.如图,在下列条件中,能判断AB∥CD的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.∠BAD+∠ADC=180° D.∠3=∠4
3.如图,能判断的条件是( )
A. B.
C. D.
4.下列说法中正确的个数为( )
①不相交的两条直线叫做平行线;
②平面内,过一点有且只有一条直线与已知直线垂直;
③平行于同一条直线的两条直线互相平行;
④在同一平面内,两条直线不是平行就是相交.
A.1个 B.2个 C.3个 D.4个
5.用反证法证明:“在同一个平面内,若则”时,应假设( )
A.不垂直于 B.与相交 C.不垂直于 D.都不垂直于
6.如图是利用直尺和三角板过直线外一点作直线的平行线的方法,这样做的依据是( )
A.同位角相等,两直线平行 B.两直线平行,同位角相等
C.两直线平行,内错角相等 D.内错角相等,两直线平行
7.如图,点在的边上,用尺规作出了,作图痕迹中,是( ).
A.以点为圆心,为半径的弧 B.以点为圆心,为半径的弧
C.以点为圆心,为半径的弧 D.以点为圆心,为半径的弧
8.如图,下列条件:①;②;③ ;④,其中能判定的是( )
A.①② B.②③ C.①④ D.②④
9.如图,直线a、b被直线c所截,给出下列条件:①∠3=∠6;②∠1=∠8;③∠4+∠7=180°;④∠5+∠1=180°.其中能判断a∥b的是( )
A.①③④ B.①②③ C.②④ D.①②
10.如图,已知直线a、b、c,若∠1=∠2=60°,且∠2=∠3,则图中平行线组数为( )
A.0 B.1 C.2 D.3
二、填空题
11.如图,点在延长线上,四个条件中:①;②,③;④;⑤,能判断的是______.(填序号).
12.如图,点E在的延长线上,下列四个条件:①;②;③;④.其中能判断的是__________________(填写正确的序号即可).
13.如图,点在的延长线上,给出的五个条件:①;②;③;④;⑤.能判断的有___________.
14.如图,下列条件中:①∠BAD+∠ABC=180°;②∠1=∠2;③∠3=∠4;④∠BAD=∠BCD,能判定AD∥BC的是_____.
15.如图,要使 AD∥BC,必须使_____(写出你认为正确的一个条件即可).
16.如图所示,请你添加一个条件使得,______.
三、解答题
17.如图,已知平分,点D在射线上,且.判断与的位置关系,并说明理由.
18.综合与探究
问题情境:如图,已知平分,于点D,E为延长线上一点,于点F,平分交于点G,.
问题发现:(1)如图1,当时,____________°;
(2)如图2,当为锐角时,与有什么数量关系,请说明理由;
拓展探究
(3)在(2)的条件下,已知直角三角形中两个锐角的和是90°,试探究和的位置关系,并证明结论;
(4)如图3,当为锐角时,若点E为线段上一点,于点F,平分交于点H,.请写出一个你发现的正确结论.
19.如图,AB∥CD,∠B=70°,∠BCE=20°,∠CEF=130°,请判断AB与EF的位置关系,并说明理由.
20.如图所示:
(1)若,,,求证:.
(2)若把(1)中的题设“”与结论“”对调,所得命题是否是真命题?说明理由.
参考答案
1.D
2.C
3.A
4.C
5.B
6.A
7.D
8.C
9.B
10.D
11.②③
12.②③④
13.②③⑤
14.①②③
15.∠ADB=∠CBD(答案不唯一)
16.(答案不唯一).
17.BC∥DE;理由见解析
【详解】
解:BC∥DE;理由如下:
因为平分,
所以∠ABE=∠CBE,
因为,
所以∠CBE=∠BED,
所以BC∥DE.
18.(1)90;(2),理由见解析;(3),证明见解析;(4)答案不唯一,例如
【详解】
(1)∵,
∴,
∵,
∴,
∵平分,平分,
∴∠1=∠AOB=45,∠2=∠DEF=45,
∴;
故答案为:90;
(2).
理由如下:∵,分别是,的平分线,
∴,,
∴,
∵,
∴;
(3)和的位置关系为OC∥GE.
证明:∵于点,
∴.
∴.
∵,
∴,
∴OC∥GE;
(4)答案不唯一,例如.
理由如下:∵,分别是,的平分线,
∴,,
∴,
∵,
∴;
19.AB∥EF.理由见解析.
【详解】
AB∥EF,理由如下:
∵AB∥CD,
∴∠B=∠BCD,∵∠B=70°,
∴∠BCD=70°,∵∠BCE=20°,
∴∠ECD=50°,
∵CEF=130°,
∴∠E+∠DCE=180°,
∴EF∥CD,
∴AB∥EF.
20.(1)详见解析;(2)是真命题.
【详解】
解:(1)证明:(已知),
.(两直线平行,内错角相等),
(已知),
(等量代换),
.(同位角相等,两直线平行),
.(两直线平行,同位角相等),
.(垂直的定义);
(2)是真命题,理由如下:
(已知),
,
.(同位角相等,两直线平行),
.(两直线平行,同位角相等),
(已知),
.(等量代换),
.(内错角相等,两直线平行).
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
