鲁教版 七下第十章第三节直角三角形同步课时训练(word版含答案)
文档属性
| 名称 | 鲁教版 七下第十章第三节直角三角形同步课时训练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 476.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 10:44:39 | ||
图片预览


文档简介
第十章第三节直角三角形同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
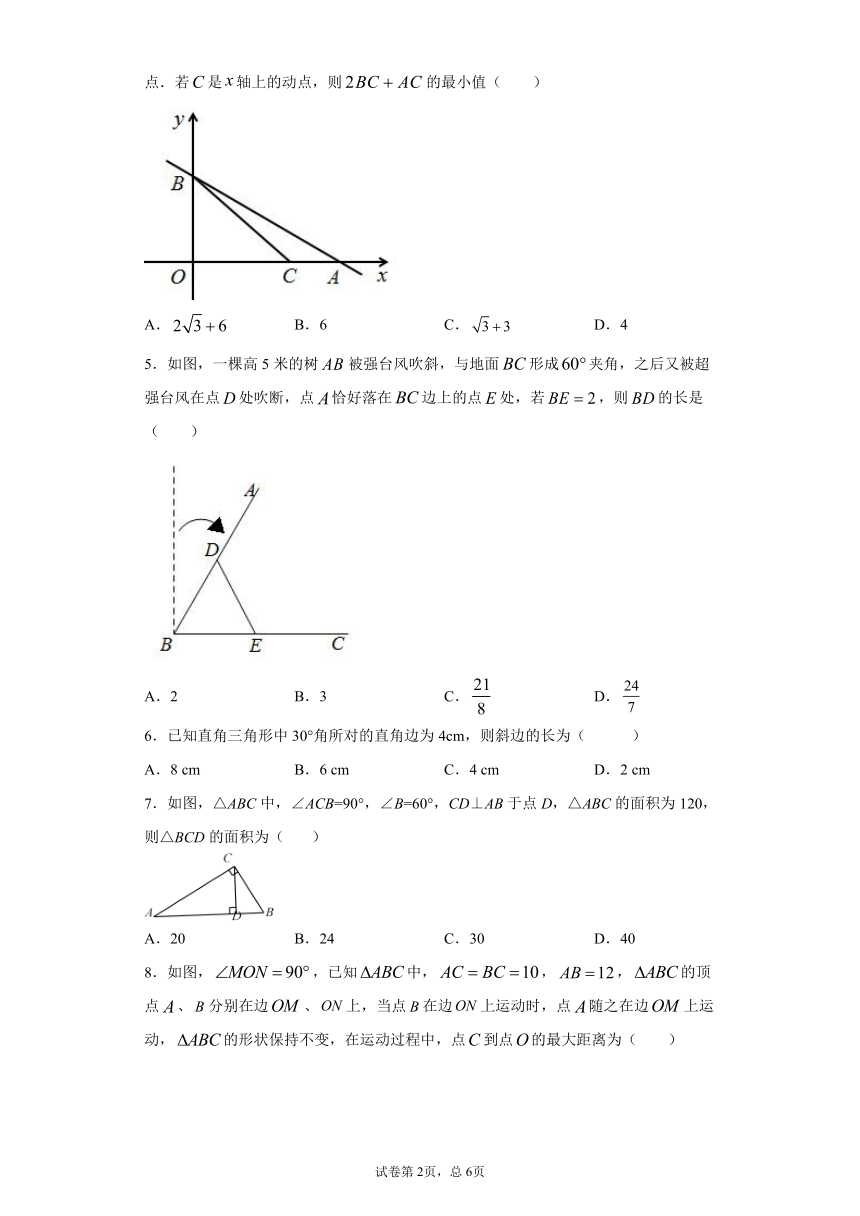
1.如图,在中,,点在线段上,且,,,则的长度为( )
A. B. C.2 D.
2.如图所示,在中,,,D是BC的中点,连接AD,,垂足为E,则AE的长为( )
A.4 B.6 C.2 D.1
3.如图,在中,,点是的中点,交于;点在上,,,,则的长为( )
A.12 B.10 C.8 D.6
4.如图,平面直角坐标系中,一次函数分别交轴、轴于、两点.若是轴上的动点,则的最小值( )
A. B.6 C. D.4
5.如图,一棵高5米的树被强台风吹斜,与地面形成夹角,之后又被超强台风在点处吹断,点恰好落在边上的点处,若,则的长是( )
A.2 B.3 C. D.
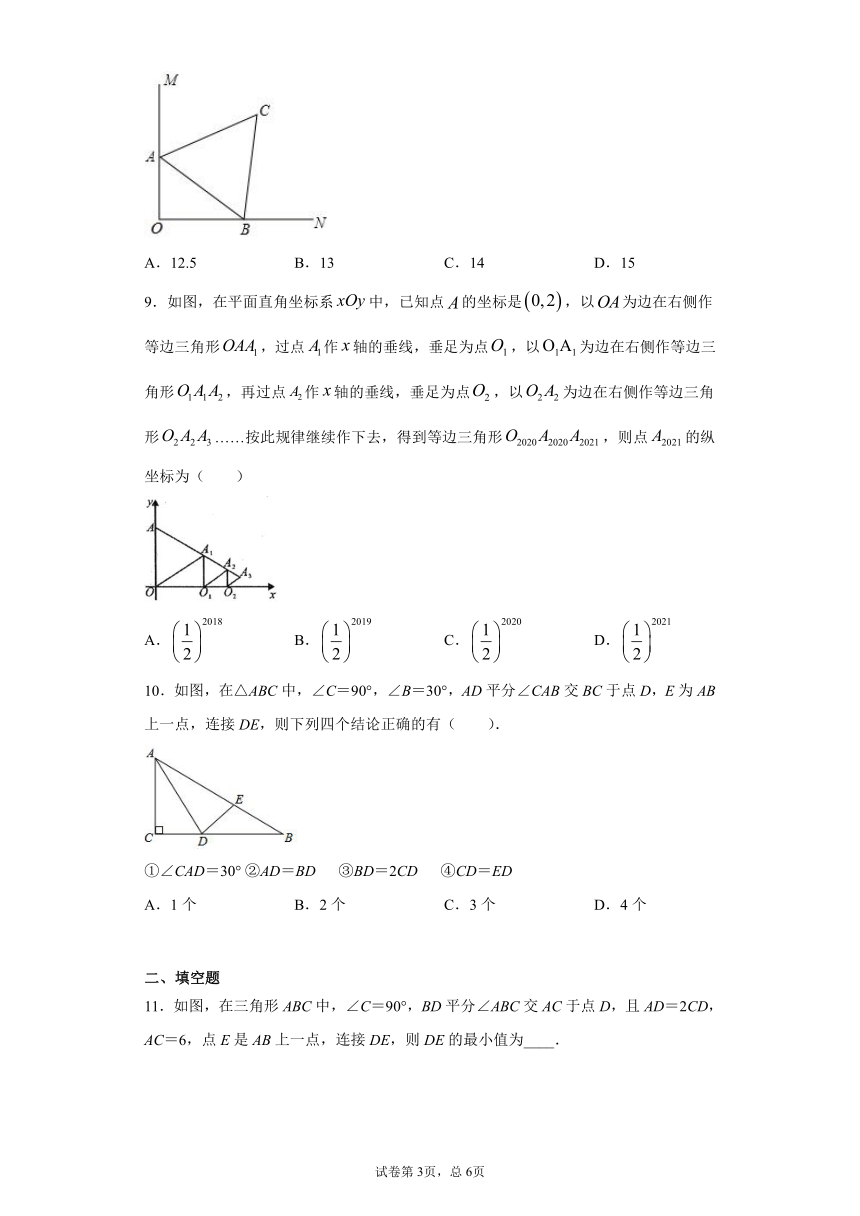
6.已知直角三角形中30°角所对的直角边为4cm,则斜边的长为( )
A.8 cm B.6 cm C.4 cm D.2 cm
7.如图,△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,△ABC的面积为120,则△BCD的面积为(??? )
A.20 B.24 C.30 D.40
8.如图,,已知中,,,的顶点、分别在边、上,当点在边上运动时,点随之在边上运动,的形状保持不变,在运动过程中,点到点的最大距离为( )
A.12.5 B.13 C.14 D.15
9.如图,在平面直角坐标系中,已知点的坐标是,以为边在右侧作等边三角形,过点作轴的垂线,垂足为点,以为边在右侧作等边三角形,再过点作轴的垂线,垂足为点,以为边在右侧作等边三角形……按此规律继续作下去,得到等边三角形,则点的纵坐标为( )
A. B. C. D.
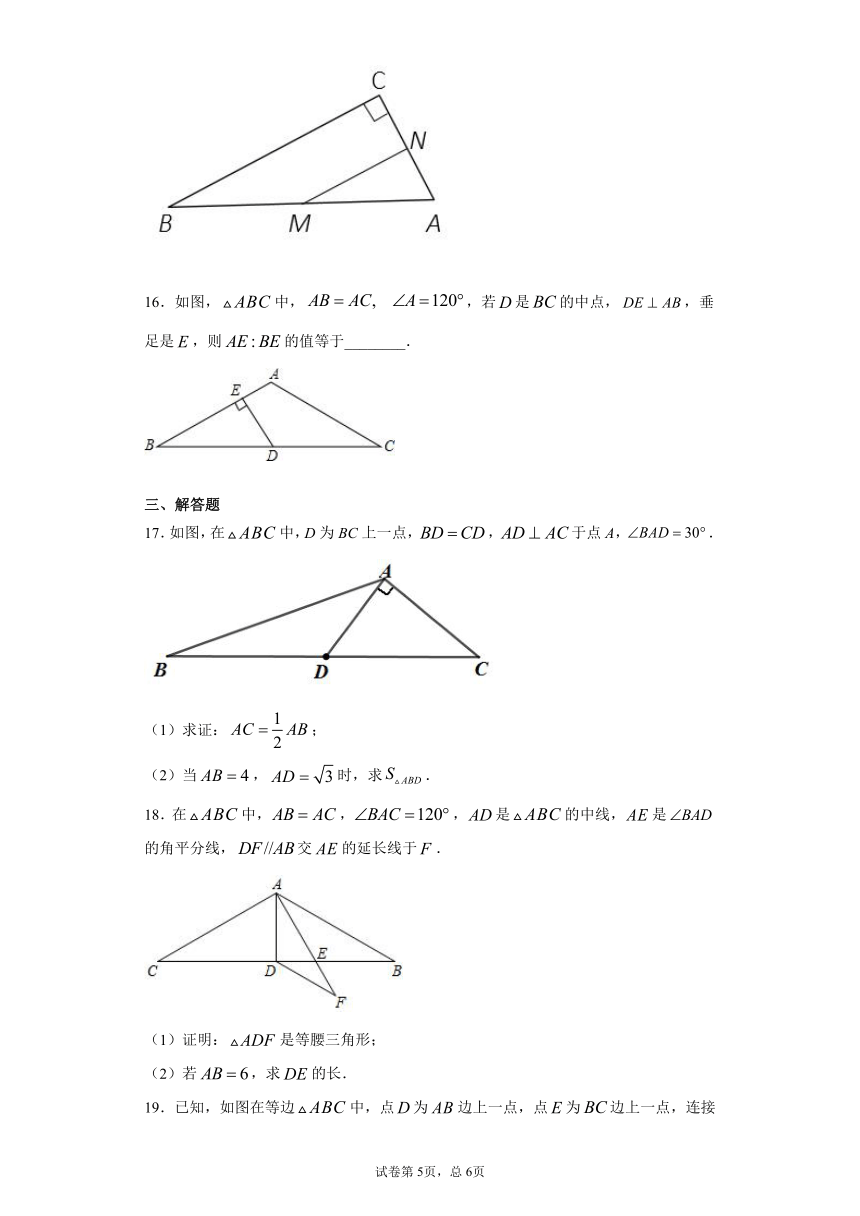
10.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB交BC于点D,E为AB上一点,连接DE,则下列四个结论正确的有( ).
①∠CAD=30° ②AD=BD ③BD=2CD ④CD=ED
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在三角形ABC中,∠C=90°,BD平分∠ABC交AC于点D,且AD=2CD,AC=6,点E是AB上一点,连接DE,则DE的最小值为____.
12.如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,DC′与AB交于点A′,连接AC′,若AD=AC′=4,BD=6,则点D到BC的距离为_____.
13.如图,在平面直角坐标系中,,,以为直角边作,并使,再以为直角边作,并使,再以为直角边作,并使,…,按此规律进行下去,则的坐标是_______.
14.已知,在等腰中,于点,且,则等腰底角的度数为_________.
15.如图,在中,,,,若点M从点B出发以的速度向点A运动,点N从点A出发以的速度向点C运动,设M,N分别从点B,A同时出发,运动的时间为,当_______s时,是为底边的等腰三角形.
16.如图,中,,若是的中点,,垂足是,则的值等于________.
三、解答题
17.如图,在中,D为BC上一点,,于点A,.
(1)求证:;
(2)当,时,求.
18.在中,,,是的中线,是的角平分线,交的延长线于.
(1)证明:是等腰三角形;
(2)若,求的长.
19.已知,如图在等边中,点为边上一点,点为边上一点,连接并延长交延长线于点,过点作交于点.
(1)求证:;
(2)当时,试判断以为顶点的三角形的形状,并说明理由;
(3)当点在线段上运动时,试探究与的数量关系,并证明你的结论.
20.已知,△ABC和△DCE都是等边三角形,点B,C,E三点不在一条直线上(如图1).
(1)求证:BD=AE;
(2)若∠ADC=30°,AD=4,CD=5,求BD的长;
(3)若点B,C,E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为3和5,求AD的长.
参考答案
1.B
2.C
3.C
4.B
5.C
6.A
7.C
8.C
9.C
10.C
11.2
12.
13.(,)
14.45°或15°或75°
15.
16.
17.(1)见详解;(2)
【详解】
(1)证明:如图,延长AD到E,使DE=AD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴BE=AC,∠E=∠CAD=90°,
∵∠BAD=30°,
∴BE=AB,
∴;
(2)解:∵AB=4,
∴BE=×4=2,
∴S△ABD=AD?BE=× ×2=.
18.(1)见解析;(2);
【详解】
(1)∵是的角平分线,∴ ;
∵ ,∴ ,
∴ ,
∴ ,
∴ 是等腰三角形
(2)∵ 是等腰三角形,为底边的中点,
∴ ,,
∵ ,
∴ ;
∴
∵ 中,,
∴
∵ 中,,
∴ .
19.(1)证明见详解;(2)以为顶点的三角形的形状是等边三角形,证明见详解(3)=.证明见详解.
【详解】
证明:(1)过点D作DH∥AC交BC于H,
则∠DHB=∠ACB,
∵是等边三角形,
所以AB=AC,∠B=∠ACB=60°,
∴∠B=∠DHB=60°,
∴DB=DH,
∵作法DH∥AC,
∴∠HBE=∠F,∠DHE=∠FCE,
∵,
∴△DEH≌△FEC(AAS),
∴DH=FC,
∴BD=CF;
(2)以为顶点的三角形的形状是等边三角形,
连结DG,
∵ED⊥AB于D,
∴∠B+∠DEB=90°,∠B=60°,
∴∠DEB=90°-∠B=30°,
又∵,∠ACB=60°,
∴∠DEB+∠GED=90°,∠EGC+∠GCE=90°,
∴∠GED=90°-∠DEB=60°,∠EGC=90°-∠GCE=30°,
由(1)知DH=BD,∠B=60°,
∴△BHD为等边三角形,
∴∠BDH=60°,
∴∠HDE=90°-∠BDH=30°,
∠F=∠HDE=30°,
∴∠F=∠EGC=30°,
∴GE=EF=DE,
∴△DEG为等边三角形;
(3)=.
∵,△BHD为等边三角形,
∴AB=BC,DB=BH,
∴AB-BD=BC-BH,
∴AD=HC,
∵作法DH∥AC,
∴∠HBE=∠F,∠DHE=∠FCE,
∵,
∴△DEH≌△FEC(AAS),
∴HE=CE,
∵,∠ACB=60°,
∴∠EGC+∠GCE=90°,
∴∠EGC=90°-∠GCE=30°,
∴GC=2EC=CH=AD,
∴GC=AD.
20.(1)见详解;(2);(3).
解:(1)∵△ABC和△DCE都是等边三角形,
∴BC=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE
∴△BCD≌△ACE(SAS),
∴BD=AE;
(2)∵∠ADC=30°,∠CDE=60°,
∴∠ADE=30°+60°=90°,
∵AD=4,DE=CD=5,
在直角△ADE中,由勾股定理得
,
∴;
(3)过A作AF⊥CD于F,如图:
∵∠ACB=60°,∠DCE=60°,
∴∠ACD=60°,
∵∠AFC=∠AFD=90°,
∴∠CAF=30°,
∵AC=3,CD=5,
∴,
∴,
∴,
由勾股定理,则
.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在中,,点在线段上,且,,,则的长度为( )
A. B. C.2 D.
2.如图所示,在中,,,D是BC的中点,连接AD,,垂足为E,则AE的长为( )
A.4 B.6 C.2 D.1
3.如图,在中,,点是的中点,交于;点在上,,,,则的长为( )
A.12 B.10 C.8 D.6
4.如图,平面直角坐标系中,一次函数分别交轴、轴于、两点.若是轴上的动点,则的最小值( )
A. B.6 C. D.4
5.如图,一棵高5米的树被强台风吹斜,与地面形成夹角,之后又被超强台风在点处吹断,点恰好落在边上的点处,若,则的长是( )
A.2 B.3 C. D.
6.已知直角三角形中30°角所对的直角边为4cm,则斜边的长为( )
A.8 cm B.6 cm C.4 cm D.2 cm
7.如图,△ABC中,∠ACB=90°,∠B=60°,CD⊥AB于点D,△ABC的面积为120,则△BCD的面积为(??? )
A.20 B.24 C.30 D.40
8.如图,,已知中,,,的顶点、分别在边、上,当点在边上运动时,点随之在边上运动,的形状保持不变,在运动过程中,点到点的最大距离为( )
A.12.5 B.13 C.14 D.15
9.如图,在平面直角坐标系中,已知点的坐标是,以为边在右侧作等边三角形,过点作轴的垂线,垂足为点,以为边在右侧作等边三角形,再过点作轴的垂线,垂足为点,以为边在右侧作等边三角形……按此规律继续作下去,得到等边三角形,则点的纵坐标为( )
A. B. C. D.
10.如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB交BC于点D,E为AB上一点,连接DE,则下列四个结论正确的有( ).
①∠CAD=30° ②AD=BD ③BD=2CD ④CD=ED
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,在三角形ABC中,∠C=90°,BD平分∠ABC交AC于点D,且AD=2CD,AC=6,点E是AB上一点,连接DE,则DE的最小值为____.
12.如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,DC′与AB交于点A′,连接AC′,若AD=AC′=4,BD=6,则点D到BC的距离为_____.
13.如图,在平面直角坐标系中,,,以为直角边作,并使,再以为直角边作,并使,再以为直角边作,并使,…,按此规律进行下去,则的坐标是_______.
14.已知,在等腰中,于点,且,则等腰底角的度数为_________.
15.如图,在中,,,,若点M从点B出发以的速度向点A运动,点N从点A出发以的速度向点C运动,设M,N分别从点B,A同时出发,运动的时间为,当_______s时,是为底边的等腰三角形.
16.如图,中,,若是的中点,,垂足是,则的值等于________.
三、解答题
17.如图,在中,D为BC上一点,,于点A,.
(1)求证:;
(2)当,时,求.
18.在中,,,是的中线,是的角平分线,交的延长线于.
(1)证明:是等腰三角形;
(2)若,求的长.
19.已知,如图在等边中,点为边上一点,点为边上一点,连接并延长交延长线于点,过点作交于点.
(1)求证:;
(2)当时,试判断以为顶点的三角形的形状,并说明理由;
(3)当点在线段上运动时,试探究与的数量关系,并证明你的结论.
20.已知,△ABC和△DCE都是等边三角形,点B,C,E三点不在一条直线上(如图1).
(1)求证:BD=AE;
(2)若∠ADC=30°,AD=4,CD=5,求BD的长;
(3)若点B,C,E三点在一条直线上(如图2),且△ABC和△DCE的边长分别为3和5,求AD的长.
参考答案
1.B
2.C
3.C
4.B
5.C
6.A
7.C
8.C
9.C
10.C
11.2
12.
13.(,)
14.45°或15°或75°
15.
16.
17.(1)见详解;(2)
【详解】
(1)证明:如图,延长AD到E,使DE=AD,
在△ACD和△EBD中,
,
∴△ACD≌△EBD(SAS),
∴BE=AC,∠E=∠CAD=90°,
∵∠BAD=30°,
∴BE=AB,
∴;
(2)解:∵AB=4,
∴BE=×4=2,
∴S△ABD=AD?BE=× ×2=.
18.(1)见解析;(2);
【详解】
(1)∵是的角平分线,∴ ;
∵ ,∴ ,
∴ ,
∴ ,
∴ 是等腰三角形
(2)∵ 是等腰三角形,为底边的中点,
∴ ,,
∵ ,
∴ ;
∴
∵ 中,,
∴
∵ 中,,
∴ .
19.(1)证明见详解;(2)以为顶点的三角形的形状是等边三角形,证明见详解(3)=.证明见详解.
【详解】
证明:(1)过点D作DH∥AC交BC于H,
则∠DHB=∠ACB,
∵是等边三角形,
所以AB=AC,∠B=∠ACB=60°,
∴∠B=∠DHB=60°,
∴DB=DH,
∵作法DH∥AC,
∴∠HBE=∠F,∠DHE=∠FCE,
∵,
∴△DEH≌△FEC(AAS),
∴DH=FC,
∴BD=CF;
(2)以为顶点的三角形的形状是等边三角形,
连结DG,
∵ED⊥AB于D,
∴∠B+∠DEB=90°,∠B=60°,
∴∠DEB=90°-∠B=30°,
又∵,∠ACB=60°,
∴∠DEB+∠GED=90°,∠EGC+∠GCE=90°,
∴∠GED=90°-∠DEB=60°,∠EGC=90°-∠GCE=30°,
由(1)知DH=BD,∠B=60°,
∴△BHD为等边三角形,
∴∠BDH=60°,
∴∠HDE=90°-∠BDH=30°,
∠F=∠HDE=30°,
∴∠F=∠EGC=30°,
∴GE=EF=DE,
∴△DEG为等边三角形;
(3)=.
∵,△BHD为等边三角形,
∴AB=BC,DB=BH,
∴AB-BD=BC-BH,
∴AD=HC,
∵作法DH∥AC,
∴∠HBE=∠F,∠DHE=∠FCE,
∵,
∴△DEH≌△FEC(AAS),
∴HE=CE,
∵,∠ACB=60°,
∴∠EGC+∠GCE=90°,
∴∠EGC=90°-∠GCE=30°,
∴GC=2EC=CH=AD,
∴GC=AD.
20.(1)见详解;(2);(3).
解:(1)∵△ABC和△DCE都是等边三角形,
∴BC=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE
∴△BCD≌△ACE(SAS),
∴BD=AE;
(2)∵∠ADC=30°,∠CDE=60°,
∴∠ADE=30°+60°=90°,
∵AD=4,DE=CD=5,
在直角△ADE中,由勾股定理得
,
∴;
(3)过A作AF⊥CD于F,如图:
∵∠ACB=60°,∠DCE=60°,
∴∠ACD=60°,
∵∠AFC=∠AFD=90°,
∴∠CAF=30°,
∵AC=3,CD=5,
∴,
∴,
∴,
由勾股定理,则
.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
