鲁教版九年级下册5.8正多边形与圆同步课时训练(word版含答案)
文档属性
| 名称 | 鲁教版九年级下册5.8正多边形与圆同步课时训练(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 507.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 11:06:51 | ||
图片预览



文档简介
鲁教版九年级下册5.8正多边形与圆同步课时训练
学校:___________姓名:___________班级:___________考号:___________
一、单选题
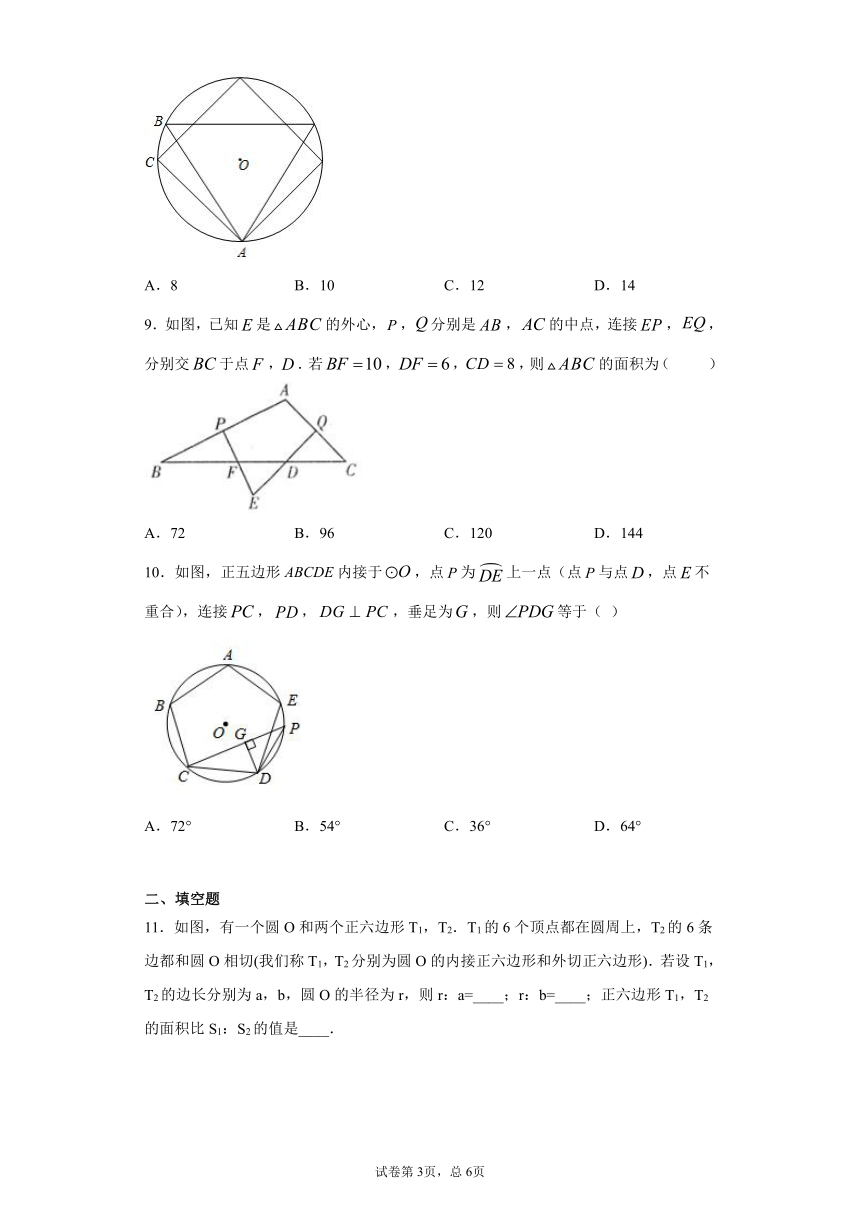
1.如图,已知△ABC内接于⊙O,∠ABC=45°,∠C=65°,点D是的中点,则∠OAD的大小为( )
A.5° B.10° C.15° D.20°
2.如图所示,为的内接三角形,,则的内接正方形的面积( )
A. B. C. D.
3.如图,将边长为6的正六边形沿折叠,点恰好落在边的中点上,延长交于点,则的长为( )
A.1 B. C. D.
4.如图,两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上,点P在上,则tan∠API的值是( )
A.2 B.2 C.2 D.1
5.如图,中,,,,是的外接圆,点是优弧上任意一点(不包括点,),记四边形的周长为,的长为,则关于的函数关系式是( )
A. B. C. D.
6.已知点O是的外心,作正方形,下列说法:①点O是的外心;②点O是的外心;③点O是的外心;④点O是的外心.其中说法一定正确的是( )
A.②④ B.①③ C.②③④ D.①③④
7.中,斜边,其重心与外心之间的距离为( )
A.2 B.3 C.4 D.6
8.如图,,分别为的内接正三角形和内接正四边形的一边,若恰好是同圆的一个内接正边形的一边,则的值为( )
A.8 B.10 C.12 D.14
9.如图,已知是的外心,,分别是,的中点,连接,,分别交于点,.若,,,则的面积为( )
A.72 B.96 C.120 D.144
10.如图,正五边形内接于,点为上一点(点与点,点不重合),连接,,,垂足为,则等于( )
A.72° B.54° C.36° D.64°
二、填空题
11.如图,有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).若设T1,T2的边长分别为a,b,圆O的半径为r,则r:a=____;r:b=____;正六边形T1,T2的面积比S1:S2的值是____.?
12.如图,ABC的内切圆与三边分别相切于点D、E、F,若∠B=50°,则∠EDF=_____度.
13.如图,四边形是的内接四边形,且, ,垂足分别为,若,则_____.
14.如图,在正方形中,,点H在上,且,点E绕点B旋转,且,同时在上方作正方形,则线段的最小值是___________.
15.已知⊙O的内接正六边形的边心距为,则⊙O的周长为_____.
16.已知正六边形的半径是3,则这个正六边形的边长是______.
三、解答题
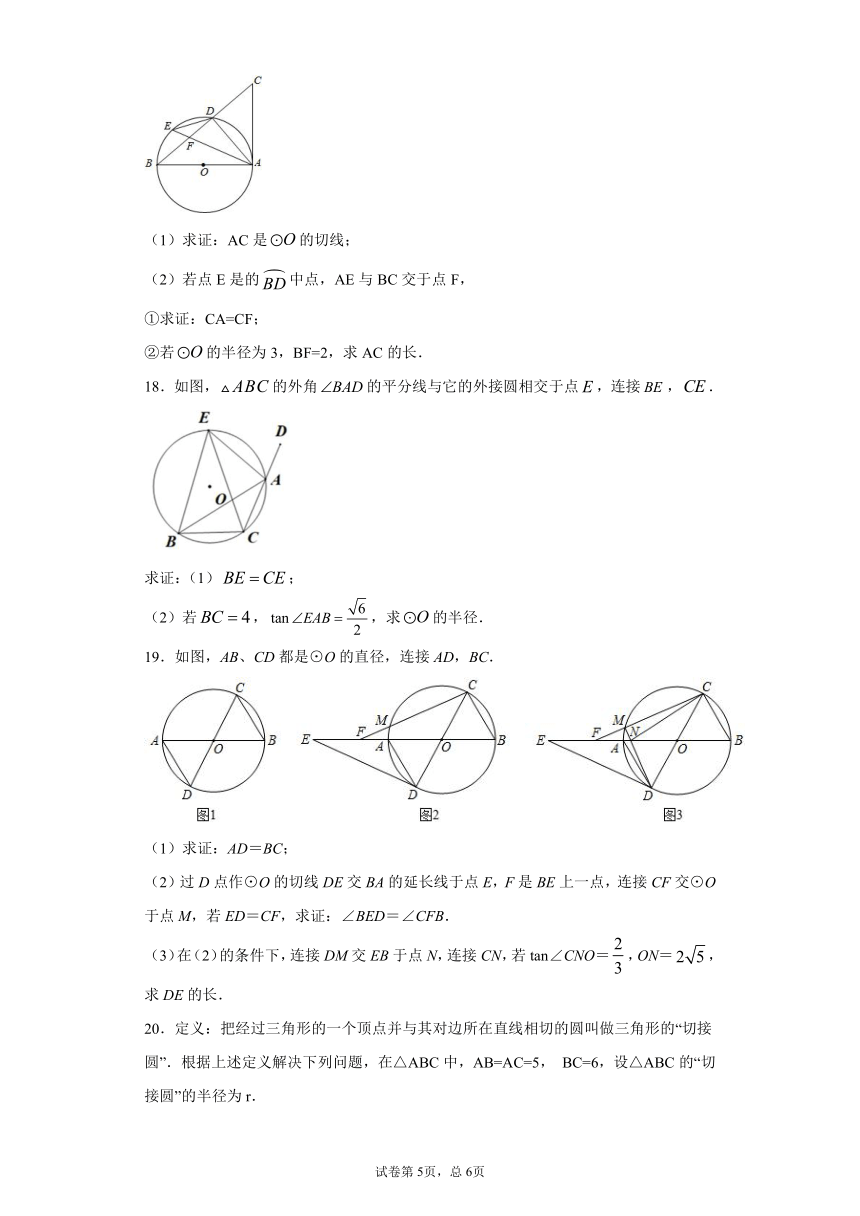
17.如图,AB是的直径,点D、E在上,连接AE、ED、DA,连接BD并延长至点C,使得.
(1)求证:AC是的切线;
(2)若点E是的中点,AE与BC交于点F,
①求证:CA=CF;
②若的半径为3,BF=2,求AC的长.
18.如图,的外角的平分线与它的外接圆相交于点,连接,.
求证:(1);
(2)若,,求的半径.
19.如图,AB、CD都是⊙O的直径,连接AD,BC.
(1)求证:AD=BC;
(2)过D点作⊙O的切线DE交BA的延长线于点E,F是BE上一点,连接CF交⊙O于点M,若ED=CF,求证:∠BED=∠CFB.
(3)在(2)的条件下,连接DM交EB于点N,连接CN,若tan∠CNO=,ON=,求DE的长.
20.定义:把经过三角形的一个顶点并与其对边所在直线相切的圆叫做三角形的“切接圆”.根据上述定义解决下列问题,在△ABC中,AB=AC=5, BC=6,设△ABC的“切接圆”的半径为r.
(1)如图1,△ABC的“切接圆”的圆心D在边AB上,求r;
(2)如图2,请确定r的最小值,并说明理由;
(3)如图3,把△ABC放在平面直角坐标系中,使点B与原点O重合,点C落在x轴正半轴上. 求证:以抛物线上任意一点为圆心都可以作△ABC的“切接圆”.
参考答案
1.B
2.C
3.A
4.A
5.B
6.B
7.A
8.C
9.B
10.B
11.1:1 :2 3:4
12.65
13.5.
14.
15.4π
16.3
17.(1)见解析;(2)①见解析;②8
【详解】
(1)∵AB是的直径,
∴∠ADB=90°,
∴∠DBA+∠DAB=90°,
∵∠DEA=∠DBA,∠DAC=∠DEA,
∴∠DBA=∠DAC,
∴∠BAC=∠DAC+∠DAB=90°,
∵AB是的直径,∠BAC=90°,
∴AC是的切线;
(2)①∵点E是的中点,
∴∠BAE=∠DAE,
∵∠CFA=∠DBA+∠BAE,∠CAF=∠DAC+∠DAE,∠DBA=∠DAC,
∴∠CFA=∠CAF,
∴CA=CF;
②设CA=CF=x,则BC=CF+BF=x+2,
∵的半径为3,
∴AB=6,
在Rt△ABC中,CA2+AB2=BC2,
即:x2+62=(x+2)2,
解得:x=8,
∴AC=8.
18.(1)见解析;(2)
【详解】
(1)由题意可得为圆内接四边形AEBC的外角
AE平分
与是同弧所对的圆周角
(2)连接EO,并延长交BC于H,连接OB,OC
EH垂直平分BC,
,
在中,
设⊙O的半径为,则
在中,由勾股定理可得:
解得:
19.(1)见解析;(2)见解析;(3)10.
【详解】
(1)证明:∵AB、CD是⊙O的直径,
∴OA=OB,OC=OD.
∵∠AOD=∠BOC,
∴△AOD≌△BOC(SAS).
∴.AD=BC.
(2)证明:如图2,过点C作CH⊥AB于H,过点D作DG⊥AB于G,
∵∠DOG=∠COH,∠DGO=∠CHO=90°,OD=OC,
∴△ODG≌△OCH(AAS).
∴DG=CH.
在Rt△EGD和Rt△FHC中,
∵DE=CF,DG=CH,
∴Rt△EGD≌Rt△FHC(HL).
∴∠BED=∠CFB.
(3)解:如图3,过点C作CH⊥AB于H,过点D作DG⊥AB于G,
∵DE为⊙O的切线,
∴∠MDE=∠MCD.
∵∠BED=∠CFB,
∴△DEN∽△CFO.
∴∠DNE=∠COF.
∴∠DNO=∠DON.
∴DN=DO.
∵DG⊥AB,ON=,
∴OG=GN=ON=.
∵△OGD≌△OHC,
∴OG=OH=.
∴NH=.
在Rt△CNH中,tan∠CNH=,
即.
∴CH=.
∴DG=.
在Rt△ODG中,由勾股定理得:OD=.
∵∠ODE=∠OGD,∠DOE=∠GOD,
∴△ODE∽△OGD.
∴.
即.
∴DE=10.
20.(1);(2);(3)证明过程见解析;
【详解】
(1)如图所示,作,,
∵AM∥DE,,AB=AC,
∴,
∴,
由题可知,
∴,
∴,
∴,
∴.
(2)由几何关系得,当这个图的直径是三角形的一条高时,最短;
∵A到BC的距离为4,
∴,;
设C到AB的距离是m,
则,
∴,
∴,,
∵>,
∴为最小值,
∴;
(3)设抛物线上任意一点为,因为抛物线的开口向上,顶点坐标为(3,2),所以对于抛物线上任意一点来说,纵坐标均为正数,
则P到x轴的距离为,
①,
∵,
∴,
∴,
将上式代入①得,
,
∴,
即说明抛物线上任意一点P均是△ABC的切接圆圆心.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知△ABC内接于⊙O,∠ABC=45°,∠C=65°,点D是的中点,则∠OAD的大小为( )
A.5° B.10° C.15° D.20°
2.如图所示,为的内接三角形,,则的内接正方形的面积( )
A. B. C. D.
3.如图,将边长为6的正六边形沿折叠,点恰好落在边的中点上,延长交于点,则的长为( )
A.1 B. C. D.
4.如图,两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上,点P在上,则tan∠API的值是( )
A.2 B.2 C.2 D.1
5.如图,中,,,,是的外接圆,点是优弧上任意一点(不包括点,),记四边形的周长为,的长为,则关于的函数关系式是( )
A. B. C. D.
6.已知点O是的外心,作正方形,下列说法:①点O是的外心;②点O是的外心;③点O是的外心;④点O是的外心.其中说法一定正确的是( )
A.②④ B.①③ C.②③④ D.①③④
7.中,斜边,其重心与外心之间的距离为( )
A.2 B.3 C.4 D.6
8.如图,,分别为的内接正三角形和内接正四边形的一边,若恰好是同圆的一个内接正边形的一边,则的值为( )
A.8 B.10 C.12 D.14
9.如图,已知是的外心,,分别是,的中点,连接,,分别交于点,.若,,,则的面积为( )
A.72 B.96 C.120 D.144
10.如图,正五边形内接于,点为上一点(点与点,点不重合),连接,,,垂足为,则等于( )
A.72° B.54° C.36° D.64°
二、填空题
11.如图,有一个圆O和两个正六边形T1,T2.T1的6个顶点都在圆周上,T2的6条边都和圆O相切(我们称T1,T2分别为圆O的内接正六边形和外切正六边形).若设T1,T2的边长分别为a,b,圆O的半径为r,则r:a=____;r:b=____;正六边形T1,T2的面积比S1:S2的值是____.?
12.如图,ABC的内切圆与三边分别相切于点D、E、F,若∠B=50°,则∠EDF=_____度.
13.如图,四边形是的内接四边形,且, ,垂足分别为,若,则_____.
14.如图,在正方形中,,点H在上,且,点E绕点B旋转,且,同时在上方作正方形,则线段的最小值是___________.
15.已知⊙O的内接正六边形的边心距为,则⊙O的周长为_____.
16.已知正六边形的半径是3,则这个正六边形的边长是______.
三、解答题
17.如图,AB是的直径,点D、E在上,连接AE、ED、DA,连接BD并延长至点C,使得.
(1)求证:AC是的切线;
(2)若点E是的中点,AE与BC交于点F,
①求证:CA=CF;
②若的半径为3,BF=2,求AC的长.
18.如图,的外角的平分线与它的外接圆相交于点,连接,.
求证:(1);
(2)若,,求的半径.
19.如图,AB、CD都是⊙O的直径,连接AD,BC.
(1)求证:AD=BC;
(2)过D点作⊙O的切线DE交BA的延长线于点E,F是BE上一点,连接CF交⊙O于点M,若ED=CF,求证:∠BED=∠CFB.
(3)在(2)的条件下,连接DM交EB于点N,连接CN,若tan∠CNO=,ON=,求DE的长.
20.定义:把经过三角形的一个顶点并与其对边所在直线相切的圆叫做三角形的“切接圆”.根据上述定义解决下列问题,在△ABC中,AB=AC=5, BC=6,设△ABC的“切接圆”的半径为r.
(1)如图1,△ABC的“切接圆”的圆心D在边AB上,求r;
(2)如图2,请确定r的最小值,并说明理由;
(3)如图3,把△ABC放在平面直角坐标系中,使点B与原点O重合,点C落在x轴正半轴上. 求证:以抛物线上任意一点为圆心都可以作△ABC的“切接圆”.
参考答案
1.B
2.C
3.A
4.A
5.B
6.B
7.A
8.C
9.B
10.B
11.1:1 :2 3:4
12.65
13.5.
14.
15.4π
16.3
17.(1)见解析;(2)①见解析;②8
【详解】
(1)∵AB是的直径,
∴∠ADB=90°,
∴∠DBA+∠DAB=90°,
∵∠DEA=∠DBA,∠DAC=∠DEA,
∴∠DBA=∠DAC,
∴∠BAC=∠DAC+∠DAB=90°,
∵AB是的直径,∠BAC=90°,
∴AC是的切线;
(2)①∵点E是的中点,
∴∠BAE=∠DAE,
∵∠CFA=∠DBA+∠BAE,∠CAF=∠DAC+∠DAE,∠DBA=∠DAC,
∴∠CFA=∠CAF,
∴CA=CF;
②设CA=CF=x,则BC=CF+BF=x+2,
∵的半径为3,
∴AB=6,
在Rt△ABC中,CA2+AB2=BC2,
即:x2+62=(x+2)2,
解得:x=8,
∴AC=8.
18.(1)见解析;(2)
【详解】
(1)由题意可得为圆内接四边形AEBC的外角
AE平分
与是同弧所对的圆周角
(2)连接EO,并延长交BC于H,连接OB,OC
EH垂直平分BC,
,
在中,
设⊙O的半径为,则
在中,由勾股定理可得:
解得:
19.(1)见解析;(2)见解析;(3)10.
【详解】
(1)证明:∵AB、CD是⊙O的直径,
∴OA=OB,OC=OD.
∵∠AOD=∠BOC,
∴△AOD≌△BOC(SAS).
∴.AD=BC.
(2)证明:如图2,过点C作CH⊥AB于H,过点D作DG⊥AB于G,
∵∠DOG=∠COH,∠DGO=∠CHO=90°,OD=OC,
∴△ODG≌△OCH(AAS).
∴DG=CH.
在Rt△EGD和Rt△FHC中,
∵DE=CF,DG=CH,
∴Rt△EGD≌Rt△FHC(HL).
∴∠BED=∠CFB.
(3)解:如图3,过点C作CH⊥AB于H,过点D作DG⊥AB于G,
∵DE为⊙O的切线,
∴∠MDE=∠MCD.
∵∠BED=∠CFB,
∴△DEN∽△CFO.
∴∠DNE=∠COF.
∴∠DNO=∠DON.
∴DN=DO.
∵DG⊥AB,ON=,
∴OG=GN=ON=.
∵△OGD≌△OHC,
∴OG=OH=.
∴NH=.
在Rt△CNH中,tan∠CNH=,
即.
∴CH=.
∴DG=.
在Rt△ODG中,由勾股定理得:OD=.
∵∠ODE=∠OGD,∠DOE=∠GOD,
∴△ODE∽△OGD.
∴.
即.
∴DE=10.
20.(1);(2);(3)证明过程见解析;
【详解】
(1)如图所示,作,,
∵AM∥DE,,AB=AC,
∴,
∴,
由题可知,
∴,
∴,
∴,
∴.
(2)由几何关系得,当这个图的直径是三角形的一条高时,最短;
∵A到BC的距离为4,
∴,;
设C到AB的距离是m,
则,
∴,
∴,,
∵>,
∴为最小值,
∴;
(3)设抛物线上任意一点为,因为抛物线的开口向上,顶点坐标为(3,2),所以对于抛物线上任意一点来说,纵坐标均为正数,
则P到x轴的距离为,
①,
∵,
∴,
∴,
将上式代入①得,
,
∴,
即说明抛物线上任意一点P均是△ABC的切接圆圆心.
