2020-2021学年湘教版数学八年级下册 2.1.1 多边形的内角和 课件(17张)
文档属性
| 名称 | 2020-2021学年湘教版数学八年级下册 2.1.1 多边形的内角和 课件(17张) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
导入新课
讲授新课
巩固提高
课堂小结
多边形的内角和
情境引入
学习目标
1.能通过不同方法探索多边形的内角和公式.
(重点)
2.学会运用多边形的内角和公式解决问题.
(难点)
在平面内,由不在同一直线的一些线段组成的封闭图形叫做多边形
组成多边形的各条线段叫做多边形的边,相邻两条边的公共端点叫做多边形的顶点,
连接不相邻的两个顶点的线段叫做多边形的对角线
相邻两边组成的角叫多边形的内角
在平面内,边相等角也相等的多边形叫做正多边形
法国的建筑事务所将协调坚固的蜂窝与人类天马行空的想象力结合,创造了这个“蜂巢”.
思考:你知道正六边形的内角和是多少吗?
问题2
你知道长方形和正方形的内角和是多少
度?
问题1
三角形内角和是多少度?
三角形内角和
是180°.
都是360°.
问题3
猜想任意四边形的内角和是多少度?
讲授新课
多边形的内角和
一
猜想:四边形ABCD的内角和是360°.
问题4
你能用以前学过的知识说明一下你的结论吗?
猜想与证明
方法1:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
A
C
D
E
B
A
B
C
D
E
F
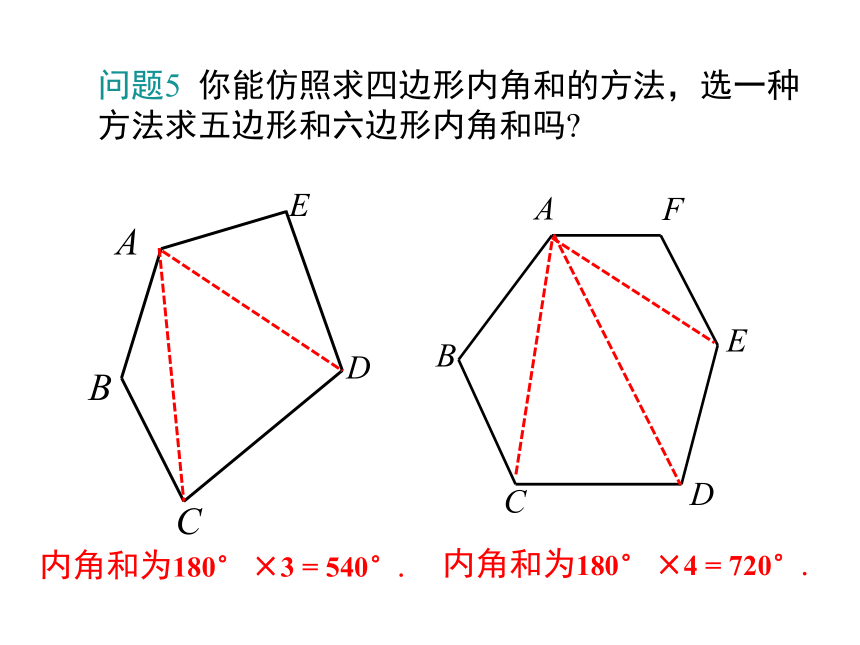
问题5
你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗?
内角和为180°
×3
=
540°.
内角和为180°
×4
=
720°.
n
边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n
-3
1
2
3
1
2
3
4
n
-2
(
n
-2
)·180?
1×180?=180?
2×180?=360?
3×180?=540?
4×180?=720?
······
······
······
······
由特殊到一般
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+
∠C
=180°.
∠A+∠B+∠C+∠D=(4-2)
×180
°=
360
°,
因为
∠B+∠D=
360°-(∠A+∠C)
=
360°-
180°
=180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
典例精析
A
B
C
D
E
方法2:如图,在CD边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
方法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
结论:四边形的内角和为360°.
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
转化思想
总结归纳
多边形的内角和公式
n边形内角和等于(n-2)×180
°.
1.一个多边形的内角和不可能是(
)
A.1800°
B.540
°
C.720
°
D.810
°
D
2.一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于(
)
A.360°
B.540
°
C.720
°
D.900
°
C
巩固提高
3.一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则
(n-2)?180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
(8-2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
课堂小结
多边形的内角和
内角和计算公式
(n-2)
×
180
°(n
≥3的整数)
正多
边形
内角=
思考.一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
解:∵1800÷180=10,
∴原多边形边数为10+2=12.
∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,
∴新多边形的边数可能是11,12,13,
∴新多边形的内角和可能是1620°,1800°,1980°.
谢谢
再见
导入新课
讲授新课
巩固提高
课堂小结
多边形的内角和
情境引入
学习目标
1.能通过不同方法探索多边形的内角和公式.
(重点)
2.学会运用多边形的内角和公式解决问题.
(难点)
在平面内,由不在同一直线的一些线段组成的封闭图形叫做多边形
组成多边形的各条线段叫做多边形的边,相邻两条边的公共端点叫做多边形的顶点,
连接不相邻的两个顶点的线段叫做多边形的对角线
相邻两边组成的角叫多边形的内角
在平面内,边相等角也相等的多边形叫做正多边形
法国的建筑事务所将协调坚固的蜂窝与人类天马行空的想象力结合,创造了这个“蜂巢”.
思考:你知道正六边形的内角和是多少吗?
问题2
你知道长方形和正方形的内角和是多少
度?
问题1
三角形内角和是多少度?
三角形内角和
是180°.
都是360°.
问题3
猜想任意四边形的内角和是多少度?
讲授新课
多边形的内角和
一
猜想:四边形ABCD的内角和是360°.
问题4
你能用以前学过的知识说明一下你的结论吗?
猜想与证明
方法1:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
A
C
D
E
B
A
B
C
D
E
F
问题5
你能仿照求四边形内角和的方法,选一种方法求五边形和六边形内角和吗?
内角和为180°
×3
=
540°.
内角和为180°
×4
=
720°.
n
边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
······
0
n
-3
1
2
3
1
2
3
4
n
-2
(
n
-2
)·180?
1×180?=180?
2×180?=360?
3×180?=540?
4×180?=720?
······
······
······
······
由特殊到一般
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+
∠C
=180°.
∠A+∠B+∠C+∠D=(4-2)
×180
°=
360
°,
因为
∠B+∠D=
360°-(∠A+∠C)
=
360°-
180°
=180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
典例精析
A
B
C
D
E
方法2:如图,在CD边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
方法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
结论:四边形的内角和为360°.
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
转化思想
总结归纳
多边形的内角和公式
n边形内角和等于(n-2)×180
°.
1.一个多边形的内角和不可能是(
)
A.1800°
B.540
°
C.720
°
D.810
°
D
2.一个多边形从一个顶点可引对角线3条,这个多边形
内角和等于(
)
A.360°
B.540
°
C.720
°
D.900
°
C
巩固提高
3.一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,这个多边形的每个内角是多少度?
解:设这个多边形边数为n,则
(n-2)?180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
(8-2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
课堂小结
多边形的内角和
内角和计算公式
(n-2)
×
180
°(n
≥3的整数)
正多
边形
内角=
思考.一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
解:∵1800÷180=10,
∴原多边形边数为10+2=12.
∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,
∴新多边形的边数可能是11,12,13,
∴新多边形的内角和可能是1620°,1800°,1980°.
谢谢
再见
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
