人教版八年级数学下册课件-18.1.1 平行四边形的性质43(共18张ppt)
文档属性
| 名称 | 人教版八年级数学下册课件-18.1.1 平行四边形的性质43(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 13:36:29 | ||
图片预览



文档简介
(共18张PPT)
八年级
下册
18.1.1 平行四边形的性质(1)
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
自学模块---温故知新
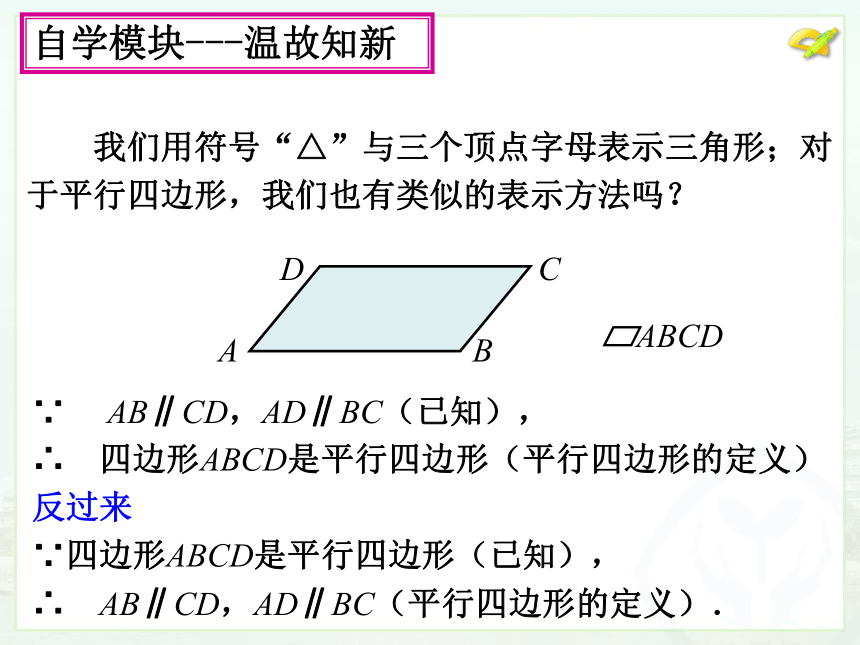
∵
AB∥CD,AD∥BC(已知),
∴ 四边形ABCD是平行四边形(平行四边形的定义)
反过来
∵四边形ABCD是平行四边形(已知),
∴ AB∥CD,AD∥BC(平行四边形的定义).
.
自学模块---温故知新
我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗?
A
B
C
D
ABCD
对于平行四边形,从定义出发,你能得出它的性质
吗?
你能证明这些结论吗?
互动模块---合作探究
给出图形定义→研究图形性质→探索图形判定条件
回忆我们的学习经历,研究几何图形的一般思路是
什么?
猜想:平行四边形对角相等,对边相等.
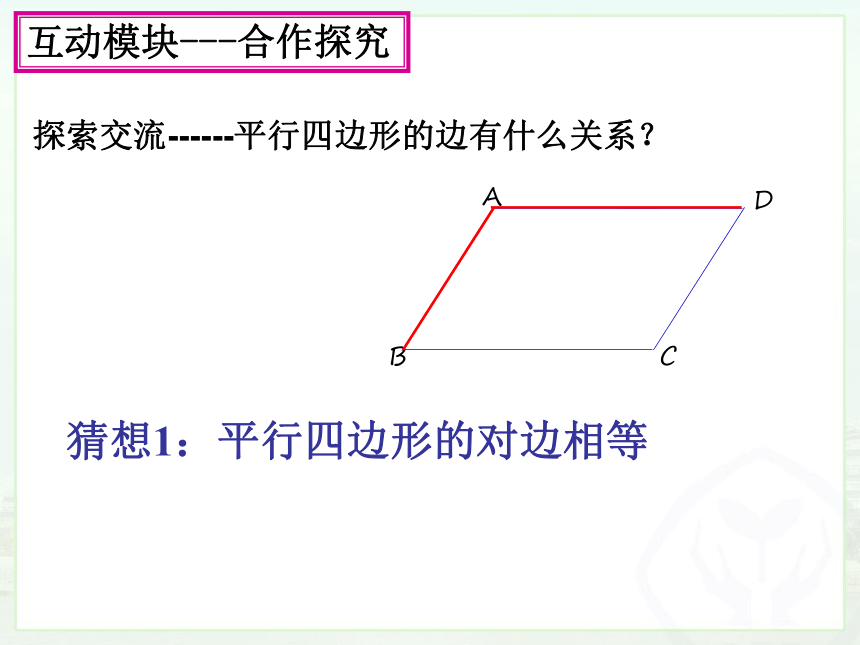
探索交流------平行四边形的边有什么关系?
C
B
A
D
猜想1:平行四边形的对边相等
互动模块---合作探究
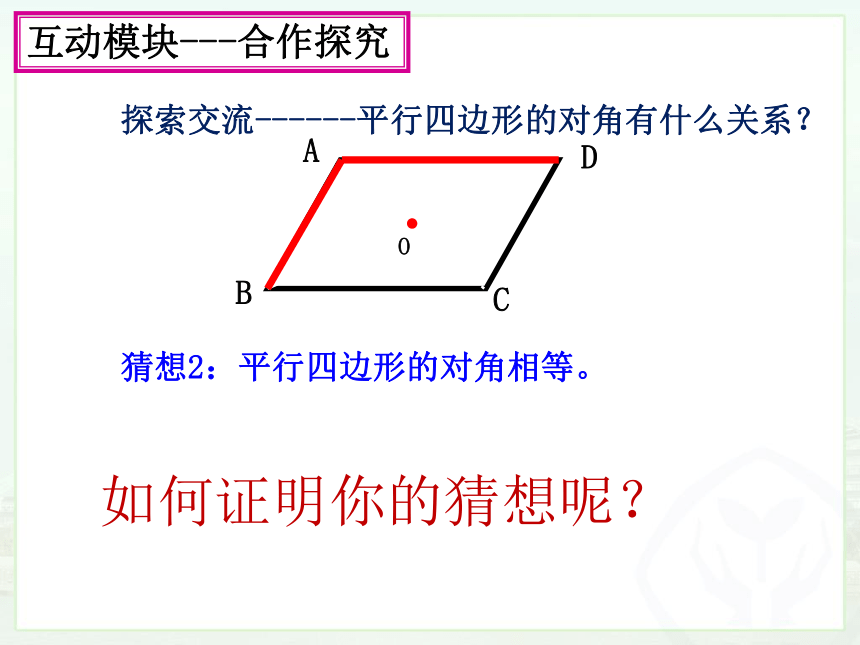
探索交流------平行四边形的对角有什么关系?
A
B
C
D
O
猜想2:平行四边形的对角相等。
互动模块---合作探究
如何证明你的猜想呢?
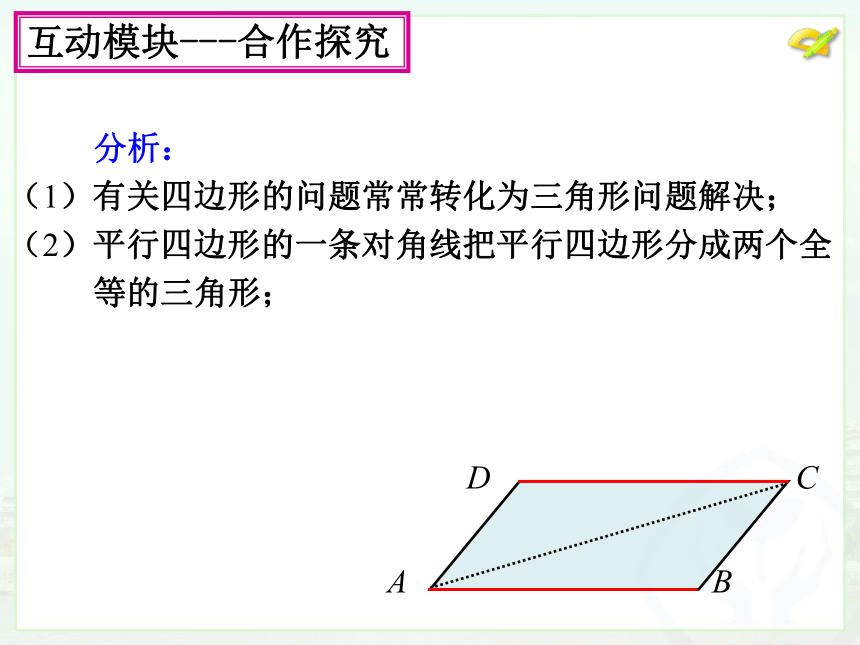
分析:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全
等的三角形;
A
B
C
D
互动模块---合作探究
归纳:
(3)平行四边形的性质定理:平行四边形的对边相等,
平行四边形的对角相等.
∵ 四边形ABCD是平行四边形(已知),
∴ AB=CD,AD=BC(平行四边形的性质);
∠DAB=∠DCB,∠B=∠D(平行四边形的性质).
A
B
C
D
互动模块---合作探究
互动模块---展示交流
B
C
D
A
问题1 如图,在 ABCD中,∠B=40°,求其余三个角的度数.
问题2 如图,在 ABCD中,AD=8,其周长为24,
求其余三条边的长度.
上图的平行四边形ABCD中有几对全等三角形?
B
A
D
C
O
互动模块---展示交流
DE=BF
吗?
例1
如图,
ABCD中,DE⊥AB,BF⊥CD,垂
足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
互动模块---合作探究
例2 如图,直线a∥b,A,B为直线a上的任意两
点,点A
到直线b
的距离和点B
到直线b
的距离相等吗?
为什么?
A
B
C
D
b
a
平行线间的距离
互动模块---合作探究
3.两条平行线中,一条直线上任意一点到另一条直线的
离,叫做这两条平行线之间的距离。
1.平行四边形的定义
2.平行四边形的性质
A
D
B
C
40
1.在
ABCD
中,AD=40,CD=30,
∠B=60°,则BC=
;AB=
;
∠A=
,
∠C=
,
∠D=
30
120°
120°
60°
2.在
ABCD
中,∠ADC=120°,
∠CAD=20°,则∠ABC=
,
∠CAB=
120°
40°
5、如果平行四边行中有两个内角的度数
比为1:2,你能求出这个平行四边形的每个内角的度数吗?
4、在
ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4
B.1:2:2:1
C.1:1:2:2
D.2:1:2:1
3、在
ABCD中,
∠B的平分线BE交AD于E,BC=5,AB=3,
则ED的长为
。
2
D
60、120、60、120
°
°
°
°
6.如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.
A
B
C
D
E
F
谈谈本节课我们的收获:
(1)知识:
(2)方法:
(3)情感:
课堂小结
作业:必做:教科书第49页练习第1题;
选做:习题18.1第7题.
课后作业
八年级
下册
18.1.1 平行四边形的性质(1)
观察这些图片,它们是否都有平行四边形的形象?
你还记得平行四边形的定义吗?
两组对边分别平行的四边形叫做平行四边形.
自学模块---温故知新
∵
AB∥CD,AD∥BC(已知),
∴ 四边形ABCD是平行四边形(平行四边形的定义)
反过来
∵四边形ABCD是平行四边形(已知),
∴ AB∥CD,AD∥BC(平行四边形的定义).
.
自学模块---温故知新
我们用符号“△”与三个顶点字母表示三角形;对
于平行四边形,我们也有类似的表示方法吗?
A
B
C
D
ABCD
对于平行四边形,从定义出发,你能得出它的性质
吗?
你能证明这些结论吗?
互动模块---合作探究
给出图形定义→研究图形性质→探索图形判定条件
回忆我们的学习经历,研究几何图形的一般思路是
什么?
猜想:平行四边形对角相等,对边相等.
探索交流------平行四边形的边有什么关系?
C
B
A
D
猜想1:平行四边形的对边相等
互动模块---合作探究
探索交流------平行四边形的对角有什么关系?
A
B
C
D
O
猜想2:平行四边形的对角相等。
互动模块---合作探究
如何证明你的猜想呢?
分析:
(1)有关四边形的问题常常转化为三角形问题解决;
(2)平行四边形的一条对角线把平行四边形分成两个全
等的三角形;
A
B
C
D
互动模块---合作探究
归纳:
(3)平行四边形的性质定理:平行四边形的对边相等,
平行四边形的对角相等.
∵ 四边形ABCD是平行四边形(已知),
∴ AB=CD,AD=BC(平行四边形的性质);
∠DAB=∠DCB,∠B=∠D(平行四边形的性质).
A
B
C
D
互动模块---合作探究
互动模块---展示交流
B
C
D
A
问题1 如图,在 ABCD中,∠B=40°,求其余三个角的度数.
问题2 如图,在 ABCD中,AD=8,其周长为24,
求其余三条边的长度.
上图的平行四边形ABCD中有几对全等三角形?
B
A
D
C
O
互动模块---展示交流
DE=BF
吗?
例1
如图,
ABCD中,DE⊥AB,BF⊥CD,垂
足分别为E,F.求证:AE=CF.
A
B
C
D
E
F
互动模块---合作探究
例2 如图,直线a∥b,A,B为直线a上的任意两
点,点A
到直线b
的距离和点B
到直线b
的距离相等吗?
为什么?
A
B
C
D
b
a
平行线间的距离
互动模块---合作探究
3.两条平行线中,一条直线上任意一点到另一条直线的
离,叫做这两条平行线之间的距离。
1.平行四边形的定义
2.平行四边形的性质
A
D
B
C
40
1.在
ABCD
中,AD=40,CD=30,
∠B=60°,则BC=
;AB=
;
∠A=
,
∠C=
,
∠D=
30
120°
120°
60°
2.在
ABCD
中,∠ADC=120°,
∠CAD=20°,则∠ABC=
,
∠CAB=
120°
40°
5、如果平行四边行中有两个内角的度数
比为1:2,你能求出这个平行四边形的每个内角的度数吗?
4、在
ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4
B.1:2:2:1
C.1:1:2:2
D.2:1:2:1
3、在
ABCD中,
∠B的平分线BE交AD于E,BC=5,AB=3,
则ED的长为
。
2
D
60、120、60、120
°
°
°
°
6.如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.
A
B
C
D
E
F
谈谈本节课我们的收获:
(1)知识:
(2)方法:
(3)情感:
课堂小结
作业:必做:教科书第49页练习第1题;
选做:习题18.1第7题.
课后作业
