2020-2021学北师大版八年级下册数学第一章三角形的证明专项练习(Word版,无答案)
文档属性
| 名称 | 2020-2021学北师大版八年级下册数学第一章三角形的证明专项练习(Word版,无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 178.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览

文档简介
八年级数学下册第一章三角形的证明
专题练习
微笑拥抱每一天,做像向日葵般温暖的人.
专题1
全等三角形判定的常见模型
类型1
“平移”模型
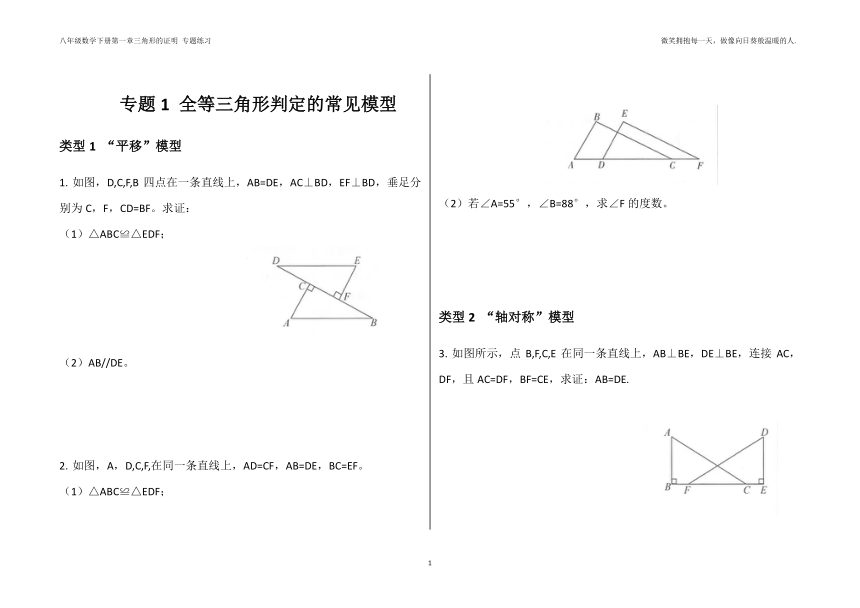
1.
如图,D,C,F,B四点在一条直线上,AB=DE,AC⊥BD,EF⊥BD,垂足分别为C,F,CD=BF。求证:
(1)△ABC≌△EDF;
(2)AB//DE。
2.
如图,A,D,C,F,在同一条直线上,AD=CF,AB=DE,BC=EF。
(1)△ABC≌△EDF;
(2)若∠A=55°,∠B=88°,求∠F的度数。
类型2
“轴对称”模型
3.
如图所示,点B,F,C,E在同一条直线上,AB⊥BE,DE⊥BE,连接AC,DF,且AC=DF,BF=CE,求证:AB=DE.
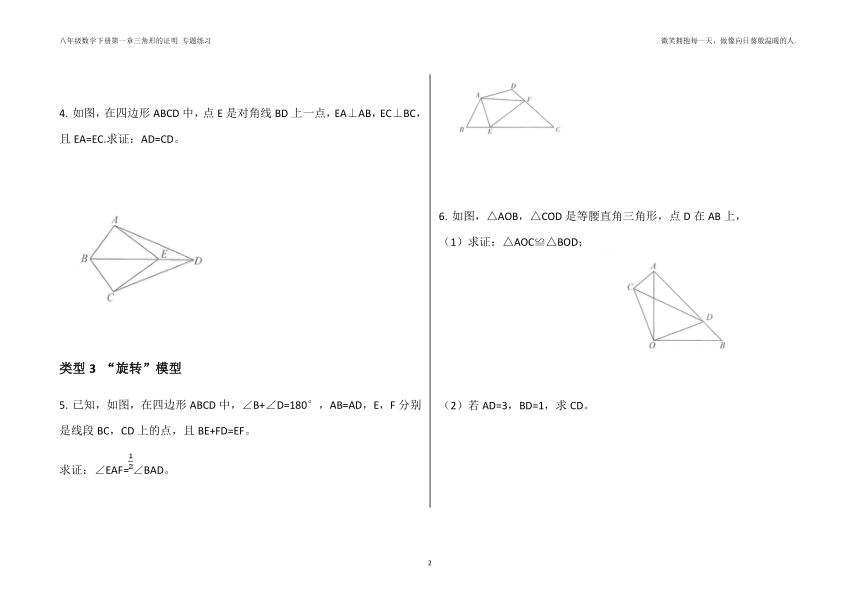
4.
如图,在四边形ABCD中,点E是对角线BD上一点,EA⊥AB,EC⊥BC,且EA=EC.求证:AD=CD。
类型3
“旋转”模型
5.
已知,如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,E,F分别是线段BC,CD上的点,且BE+FD=EF。
求证:∠EAF=∠BAD。
6.
如图,△AOB,△COD是等腰直角三角形,点D在AB上,
(1)求证:△AOC≌△BOD;
(2)若AD=3,BD=1,求CD。
专题2
线段的垂直平分线与角平分线的应用
类型1
线段的垂直平分线的应用
1.
如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于点E。
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长。
2如图,△ABC中,∠ABC=30°,∠ACB=50°,DE,FG分别为AB,AC的垂直平分线,E,G分别为垂足。
(1)直接写出∠BAC的度数;
(2)求∠DAF的度数。
类型2
角平分线的应用
3.如图,△ABC中,∠ACD=90°,AB=10,AC=6,AD平分∠BAC,DE⊥AB,垂足为E。
(1)线段AD与CE是否垂直?说明理由。
(2)求△BDE的周长。
4.
如图,在△ABC与△AED中,∠C=∠E,BC=DE,CA=EA,过点A作AF⊥DE,垂足为F,DE交CB的延长线于点G,连接AG.
(1)求证:GA平分∠DGB;
(2)若,求FG的长。
类型3
线段的垂直平分线与角平分线的综合应用
5.
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E。
求证:(1)∠EAD=∠EDA;
(2)DF//AC;
(3)∠EAC=∠B。
专题练习
微笑拥抱每一天,做像向日葵般温暖的人.
专题1
全等三角形判定的常见模型
类型1
“平移”模型
1.
如图,D,C,F,B四点在一条直线上,AB=DE,AC⊥BD,EF⊥BD,垂足分别为C,F,CD=BF。求证:
(1)△ABC≌△EDF;
(2)AB//DE。
2.
如图,A,D,C,F,在同一条直线上,AD=CF,AB=DE,BC=EF。
(1)△ABC≌△EDF;
(2)若∠A=55°,∠B=88°,求∠F的度数。
类型2
“轴对称”模型
3.
如图所示,点B,F,C,E在同一条直线上,AB⊥BE,DE⊥BE,连接AC,DF,且AC=DF,BF=CE,求证:AB=DE.
4.
如图,在四边形ABCD中,点E是对角线BD上一点,EA⊥AB,EC⊥BC,且EA=EC.求证:AD=CD。
类型3
“旋转”模型
5.
已知,如图,在四边形ABCD中,∠B+∠D=180°,AB=AD,E,F分别是线段BC,CD上的点,且BE+FD=EF。
求证:∠EAF=∠BAD。
6.
如图,△AOB,△COD是等腰直角三角形,点D在AB上,
(1)求证:△AOC≌△BOD;
(2)若AD=3,BD=1,求CD。
专题2
线段的垂直平分线与角平分线的应用
类型1
线段的垂直平分线的应用
1.
如图,已知∠BAC=60°,∠B=80°,DE垂直平分AC交BC于点D,交AC于点E。
(1)求∠BAD的度数;
(2)若AB=10,BC=12,求△ABD的周长。
2如图,△ABC中,∠ABC=30°,∠ACB=50°,DE,FG分别为AB,AC的垂直平分线,E,G分别为垂足。
(1)直接写出∠BAC的度数;
(2)求∠DAF的度数。
类型2
角平分线的应用
3.如图,△ABC中,∠ACD=90°,AB=10,AC=6,AD平分∠BAC,DE⊥AB,垂足为E。
(1)线段AD与CE是否垂直?说明理由。
(2)求△BDE的周长。
4.
如图,在△ABC与△AED中,∠C=∠E,BC=DE,CA=EA,过点A作AF⊥DE,垂足为F,DE交CB的延长线于点G,连接AG.
(1)求证:GA平分∠DGB;
(2)若,求FG的长。
类型3
线段的垂直平分线与角平分线的综合应用
5.
如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E。
求证:(1)∠EAD=∠EDA;
(2)DF//AC;
(3)∠EAC=∠B。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
