2020-2021学年八年级数学人教版下册18.1.2 平行四边形的判定 课后练习(WORD版含答案
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册18.1.2 平行四边形的判定 课后练习(WORD版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 598.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 14:28:36 | ||
图片预览




文档简介
人教版八年级数学下册
第十八章
平行四边形
18.1.2
平行四边形的判定
课后练习
一、选择题
1.下列条件中不能判定一定是平行四边形的有( )
A.一组对角相等,一组邻角互补
B.一组对边平行,另一组对边相等
C.两组对边相等
D.一组对边平行,且另一组对边也平行
2.四边形中,对角线交于点.给出下列四组条件:
①∥,∥;
②,;
③,;
④∥,.
其中一定能判定这个四边形是平行四边形的条件共有(
)
A.1组;
B.2组;
C.3组;
D.4组.
3.如图,在中,,,D是边的中点,于点D,交于点E,若,则的长是(
)
A.8
B.6
C.4
D.2
4.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC
B.AD∥BC,AB=CD
C.OA=OC,OB=OD
D.AB=CD,AD=BC
5.如图,已知四边形中,、分别为、上的点,、分别为、的中点.当点在上从点向点移动而点不动时,那么下列结论成立的是(
)
A.线段的长逐渐增大
B.线段的长不变
C.线段的长逐渐减小
D.线段的长与点的位置有关
6.如图,在中,D,F分别是,上的点,且.点E是射线上一点,若再添加下列其中一个条件后,不能判定四边形为平行四边形的是(
)
A.
B.
C.
D.
7.如图,是的中线,分别是的中点,则等于(
)
A.
B.
C.
D.
8.如图,在中,,是的中点,过点作的平行线,交于点E,作的垂线交于点,若,且的面积为1,则的长为( )
A.
B.5
C.
D.10
9.已知:点D,E分别是△ABC的边AB,AC的中点,如图所示.
求证:DE∥BC,且DE=BC.
证明:延长DE到点F,使EF=DE,连接FC,DC,AF,又AE=EC,则四边形ADCF是平行四边形,接着以下是排序错误的证明过程:
①∴DF╩BC;②∴CF╩AD.即CF╩BD;③∴四边形DBCF是平行四边形;④∴DE∥BC,且DE=BC.则正确的证明顺序应是(??
)
A.②→③→①→④
B.②→①→③→④
C.①→③→④→②
D.①→③→②→④
10.如图,分别以的斜边,直角边为边向外作等边和,为的中点,,相交于点,若,下列结论:①;②四边形为平行四边形;③;④,其中正确结论的序号是(
)
A.①②④
B.①③
C.②③④
D.①②③④
二、填空题
11.在四边形中,对角线相交于点,给出下列条件:①,;②,;③,;④,.其中能够判定是平行四边形的有______.
12.如图,四边形中,,,若,,为的中点,则的长为_______.
13.如图,在平行四边形中,平分,,连接,是的中点,连接,若,则_____.
14.如图,在
中,对角线AC、BD相交于点O,已知点E、F分别是BD上的点,请你添加一个条件_______________
,使得四边形AFCE是一个平行四边形.
15.如图,在中,点分别在边上,且,连接,点分别是的中点,,则的度数是_______.
三、解答题
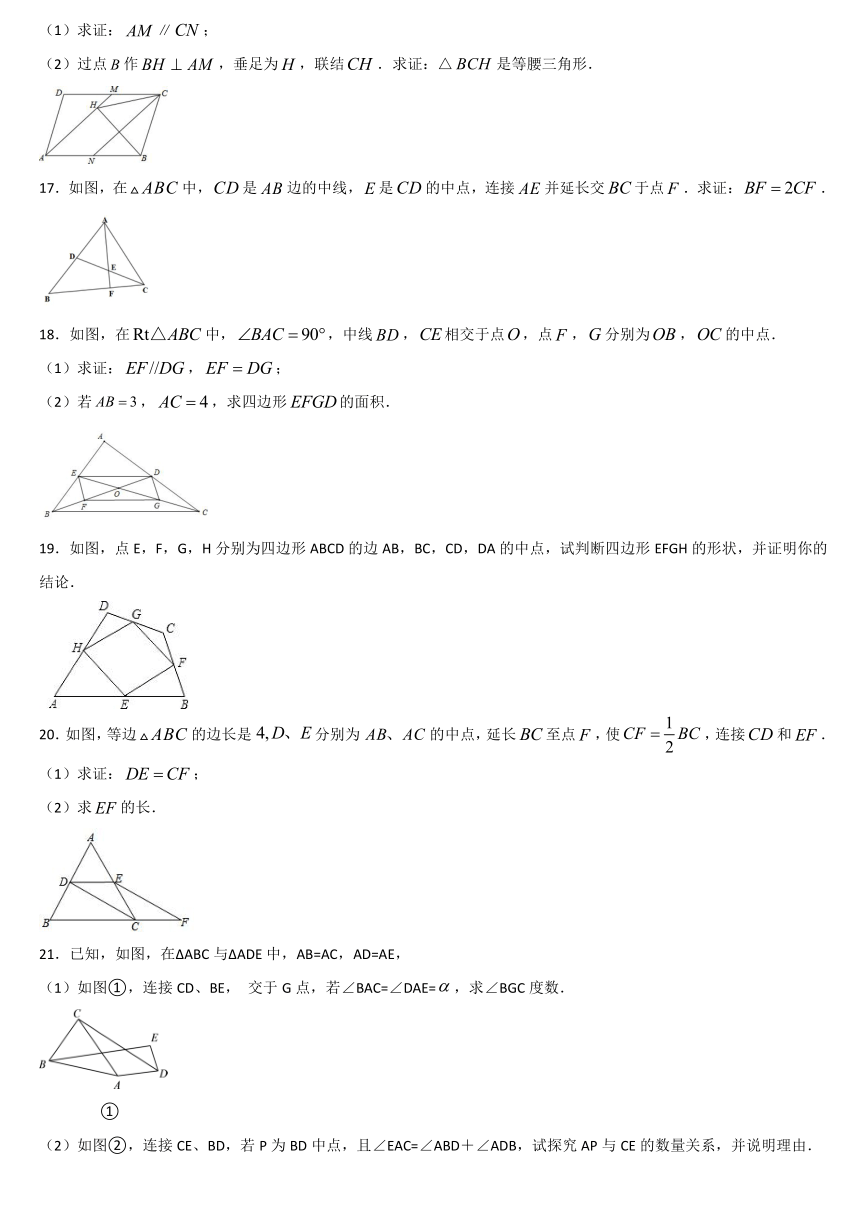
16.已知:平行四边形中,点为边的中点,点为边的中点,联结、.
(1)求证:∥;
(2)过点作,垂足为,联结.求证:△是等腰三角形.
17.如图,在中,是边的中线,是的中点,连接并延长交于点.求证:.
18.如图,在中,,中线,相交于点,点,分别为,的中点.
(1)求证:,;
(2)若,,求四边形的面积.
19.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并证明你的结论.
20.如图,等边的边长是分别为的中点,延长至点,使,连接和.
(1)求证:;
(2)求的长.
21.已知,如图,在ΔABC与ΔADE中,AB=AC,AD=AE,
(1)如图①,连接CD、BE,
交于G点,若∠BAC=∠DAE=,求∠BGC度数.
①
(2)如图②,连接CE、BD,若P为BD中点,且∠EAC=∠ABD+∠ADB,试探究AP与CE的数量关系,并说明理由.
②
22.在ABC中,∠C=90°,AC>BC,D是AB的中点,E为直线AC上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.
(1)如图1,当点E是线段AC的中点时,AE=2,BF=1,求EF的长;
(2)当点E在线段CA的延长线上时,依题意补全图形2,用等式表示AE,EF,BF之间的数量关系,并证明.
23.在平面直角坐标系中点、的坐标分别为,.
(1)如图1,若点、关于轴对称,,请直接写出的度数___________;
(2)如图2,点的坐标为,,试用字母、表示线段的长;
(3)如图3,点的坐标为,且,点的坐标分别为,试用字母、、表示线段的长
【参考答案】
1.B
2.C
3.C
4.B
5.B
6.D
7.B
8.A
9.A
10.D
11.①③④
12.
13.2
14.DE=BF
15.
16.解:(1)证明:∵四边形是平行四边形,
∴∥且.
∵点、分别是边、的中点,
∴,.
∴.
又∵∥,
∴四边形是平行四边形
∴∥.
(2)设BH与CN交于点E,
∵AM∥CN,BH⊥AM,
∴BH⊥CN,
∵N是AB的中点,
∴EN是△BAH的中位线,
∴BE=EH,
∴CN是BH的垂直平分线,
∴CH=CB,
∴△BCH是等腰三角形.
17.证明:取的中点,连接,
∵是边的中线,
∴是边的中点,
∴,
.
∴,.
∵是的中点,
∴,
在△MDE和△FCE中,
∴.
∴,
∴.
18.(1)证明:∵点,分别是,的中点,
∴,.
∵点,分别是,的中点,
∴,.
∴,.
∴四边形是平行四边形.
∴,;
(2)解:∵,
∴.
又∵,
∴.
∵,,
∵,
∵点是中点,
∴.
∴.
∴四边形的面积.
19.证明:连接AC,如图.
∵E,F分别是AB,BC的中点,
∴EF是△ABC的中位线,
∴EF∥AC,且EF=AC,
同理HG∥AC,且HG=AC,
∴EF∥HG,且EF=HG.
∴四边形EFGH是平行四边形.
20.(1)证明:∵D、E分别为AB、AC的中点,
∴DE为ABC的中位线,
∴DEBC
,DE=BC,
∵CF=BC,
∴DE=FC;
(2)解:∵DE=FC,DEFC
,
∴四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边ABC的边长是4,
∴AD=BD=2,CD⊥AB,BC=4,
∴在RtBCD中,DC=
==2,
∴EF=DC=2.
21.(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAE
=∠DAE+∠CAE,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
,
∴△BAE△CAD(SAS),
∴∠ABE=∠ACD,
∵∠ABE+∠1+∠BAC=∠ACD+∠2+∠BGC,
且∠1=∠2,∠BAC=,
∴∠BGC=∠BAC=;
(2)CE=2AP,理由如下:
延长DA至O,使OA=DA,连接OB,如图:
∵AD=AE,
∴OA=DA=AE,
∵∠EAC=∠ABD+∠ADB,
又∠BAO是△ABD的外角,
则∠BAO
=∠ABD+∠ADB,
∴∠BAO=∠EAC,
在△BAO和△CAE中,
,
∴△BAO△CAE(SAS),
∴BO
=
CE,
∵P为BD中点,
∴BO=2AP,
∴CE=2AP.
22.解:(1)∵D是AB的中点,E是线段AC的中点,
∴DE∥BC,DE=BC,
∵∠ACB=90°,
∴∠DEC=90°,
∵DF⊥DE,
∴∠EDF=90°,
∴四边形CEDF是矩形,
∴DE=CF=BC,
∴CF=BF=1,
∵CE=AE=2,
∴EF=;
(2)AE2+BF2=EF2.
证明:过点B作BM∥AC,与ED的延长线交于点M,连接MF,
则∠AED=∠BMD,∠CBM=∠ACB=90°,
∵D点是AB的中点,
∴AD=BD,
在△ADE和△BDM中,,
∴△ADE≌△BDM(AAS),
∴AE=BM,DE=DM,
∵DF⊥DE,
∴EF=MF,
∵BM2+BF2=MF2,
∴AE2+BF2=EF2.
23.解:(1)∵点、关于轴对称,
∴AB=AC,
∵,
∴=;
故答案为:27°;
(2)延长AD交x轴于点G,作DE⊥y轴于E,DF⊥x轴于F,如图,
∵,∴OE=DF=a,DE∥OG,
∵OA=a,
∴AE=OE=,
∴DE是△AOG的中位线,
∴AD=DG,
∴AD=OD=DG,
∴∠DOG=∠DGO,
∵∠ADO=∠ABO,∠AHD=∠OHB,
∴∠DAB=∠DOG,
∴∠BAD=∠BGD,
∴AB=BG,
∵DO=DG,DF⊥x轴,
∴OG=2OF=2c,
又∵OG=OB+BG=b+AB=2c,
∴AB=2c-b;
(3)连接OE,作EG⊥DB于G,EH⊥x轴于H,如图,
∵EA=ED,OA=OD=a,OE=OE,
∴△AOE≌△DOE,
∴∠AOE=∠DOE=45°,
∴OE平分∠AOD,
∵,
∴F在∠AOD的平分线上,
∴O、E、F三点共线,
设E(n,n),则,
∵ED=EB,EG⊥DB,
∴DG=BG,即n-a=b-n,可得,
在Rt△BEG中,由勾股定理得,
∵,
∴,
∴,
∴
第十八章
平行四边形
18.1.2
平行四边形的判定
课后练习
一、选择题
1.下列条件中不能判定一定是平行四边形的有( )
A.一组对角相等,一组邻角互补
B.一组对边平行,另一组对边相等
C.两组对边相等
D.一组对边平行,且另一组对边也平行
2.四边形中,对角线交于点.给出下列四组条件:
①∥,∥;
②,;
③,;
④∥,.
其中一定能判定这个四边形是平行四边形的条件共有(
)
A.1组;
B.2组;
C.3组;
D.4组.
3.如图,在中,,,D是边的中点,于点D,交于点E,若,则的长是(
)
A.8
B.6
C.4
D.2
4.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC
B.AD∥BC,AB=CD
C.OA=OC,OB=OD
D.AB=CD,AD=BC
5.如图,已知四边形中,、分别为、上的点,、分别为、的中点.当点在上从点向点移动而点不动时,那么下列结论成立的是(
)
A.线段的长逐渐增大
B.线段的长不变
C.线段的长逐渐减小
D.线段的长与点的位置有关
6.如图,在中,D,F分别是,上的点,且.点E是射线上一点,若再添加下列其中一个条件后,不能判定四边形为平行四边形的是(
)
A.
B.
C.
D.
7.如图,是的中线,分别是的中点,则等于(
)
A.
B.
C.
D.
8.如图,在中,,是的中点,过点作的平行线,交于点E,作的垂线交于点,若,且的面积为1,则的长为( )
A.
B.5
C.
D.10
9.已知:点D,E分别是△ABC的边AB,AC的中点,如图所示.
求证:DE∥BC,且DE=BC.
证明:延长DE到点F,使EF=DE,连接FC,DC,AF,又AE=EC,则四边形ADCF是平行四边形,接着以下是排序错误的证明过程:
①∴DF╩BC;②∴CF╩AD.即CF╩BD;③∴四边形DBCF是平行四边形;④∴DE∥BC,且DE=BC.则正确的证明顺序应是(??
)
A.②→③→①→④
B.②→①→③→④
C.①→③→④→②
D.①→③→②→④
10.如图,分别以的斜边,直角边为边向外作等边和,为的中点,,相交于点,若,下列结论:①;②四边形为平行四边形;③;④,其中正确结论的序号是(
)
A.①②④
B.①③
C.②③④
D.①②③④
二、填空题
11.在四边形中,对角线相交于点,给出下列条件:①,;②,;③,;④,.其中能够判定是平行四边形的有______.
12.如图,四边形中,,,若,,为的中点,则的长为_______.
13.如图,在平行四边形中,平分,,连接,是的中点,连接,若,则_____.
14.如图,在
中,对角线AC、BD相交于点O,已知点E、F分别是BD上的点,请你添加一个条件_______________
,使得四边形AFCE是一个平行四边形.
15.如图,在中,点分别在边上,且,连接,点分别是的中点,,则的度数是_______.
三、解答题
16.已知:平行四边形中,点为边的中点,点为边的中点,联结、.
(1)求证:∥;
(2)过点作,垂足为,联结.求证:△是等腰三角形.
17.如图,在中,是边的中线,是的中点,连接并延长交于点.求证:.
18.如图,在中,,中线,相交于点,点,分别为,的中点.
(1)求证:,;
(2)若,,求四边形的面积.
19.如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并证明你的结论.
20.如图,等边的边长是分别为的中点,延长至点,使,连接和.
(1)求证:;
(2)求的长.
21.已知,如图,在ΔABC与ΔADE中,AB=AC,AD=AE,
(1)如图①,连接CD、BE,
交于G点,若∠BAC=∠DAE=,求∠BGC度数.
①
(2)如图②,连接CE、BD,若P为BD中点,且∠EAC=∠ABD+∠ADB,试探究AP与CE的数量关系,并说明理由.
②
22.在ABC中,∠C=90°,AC>BC,D是AB的中点,E为直线AC上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF.
(1)如图1,当点E是线段AC的中点时,AE=2,BF=1,求EF的长;
(2)当点E在线段CA的延长线上时,依题意补全图形2,用等式表示AE,EF,BF之间的数量关系,并证明.
23.在平面直角坐标系中点、的坐标分别为,.
(1)如图1,若点、关于轴对称,,请直接写出的度数___________;
(2)如图2,点的坐标为,,试用字母、表示线段的长;
(3)如图3,点的坐标为,且,点的坐标分别为,试用字母、、表示线段的长
【参考答案】
1.B
2.C
3.C
4.B
5.B
6.D
7.B
8.A
9.A
10.D
11.①③④
12.
13.2
14.DE=BF
15.
16.解:(1)证明:∵四边形是平行四边形,
∴∥且.
∵点、分别是边、的中点,
∴,.
∴.
又∵∥,
∴四边形是平行四边形
∴∥.
(2)设BH与CN交于点E,
∵AM∥CN,BH⊥AM,
∴BH⊥CN,
∵N是AB的中点,
∴EN是△BAH的中位线,
∴BE=EH,
∴CN是BH的垂直平分线,
∴CH=CB,
∴△BCH是等腰三角形.
17.证明:取的中点,连接,
∵是边的中线,
∴是边的中点,
∴,
.
∴,.
∵是的中点,
∴,
在△MDE和△FCE中,
∴.
∴,
∴.
18.(1)证明:∵点,分别是,的中点,
∴,.
∵点,分别是,的中点,
∴,.
∴,.
∴四边形是平行四边形.
∴,;
(2)解:∵,
∴.
又∵,
∴.
∵,,
∵,
∵点是中点,
∴.
∴.
∴四边形的面积.
19.证明:连接AC,如图.
∵E,F分别是AB,BC的中点,
∴EF是△ABC的中位线,
∴EF∥AC,且EF=AC,
同理HG∥AC,且HG=AC,
∴EF∥HG,且EF=HG.
∴四边形EFGH是平行四边形.
20.(1)证明:∵D、E分别为AB、AC的中点,
∴DE为ABC的中位线,
∴DEBC
,DE=BC,
∵CF=BC,
∴DE=FC;
(2)解:∵DE=FC,DEFC
,
∴四边形DEFC是平行四边形,
∴DC=EF,
∵D为AB的中点,等边ABC的边长是4,
∴AD=BD=2,CD⊥AB,BC=4,
∴在RtBCD中,DC=
==2,
∴EF=DC=2.
21.(1)∵∠BAC=∠DAE,
∴∠BAC+∠CAE
=∠DAE+∠CAE,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
,
∴△BAE△CAD(SAS),
∴∠ABE=∠ACD,
∵∠ABE+∠1+∠BAC=∠ACD+∠2+∠BGC,
且∠1=∠2,∠BAC=,
∴∠BGC=∠BAC=;
(2)CE=2AP,理由如下:
延长DA至O,使OA=DA,连接OB,如图:
∵AD=AE,
∴OA=DA=AE,
∵∠EAC=∠ABD+∠ADB,
又∠BAO是△ABD的外角,
则∠BAO
=∠ABD+∠ADB,
∴∠BAO=∠EAC,
在△BAO和△CAE中,
,
∴△BAO△CAE(SAS),
∴BO
=
CE,
∵P为BD中点,
∴BO=2AP,
∴CE=2AP.
22.解:(1)∵D是AB的中点,E是线段AC的中点,
∴DE∥BC,DE=BC,
∵∠ACB=90°,
∴∠DEC=90°,
∵DF⊥DE,
∴∠EDF=90°,
∴四边形CEDF是矩形,
∴DE=CF=BC,
∴CF=BF=1,
∵CE=AE=2,
∴EF=;
(2)AE2+BF2=EF2.
证明:过点B作BM∥AC,与ED的延长线交于点M,连接MF,
则∠AED=∠BMD,∠CBM=∠ACB=90°,
∵D点是AB的中点,
∴AD=BD,
在△ADE和△BDM中,,
∴△ADE≌△BDM(AAS),
∴AE=BM,DE=DM,
∵DF⊥DE,
∴EF=MF,
∵BM2+BF2=MF2,
∴AE2+BF2=EF2.
23.解:(1)∵点、关于轴对称,
∴AB=AC,
∵,
∴=;
故答案为:27°;
(2)延长AD交x轴于点G,作DE⊥y轴于E,DF⊥x轴于F,如图,
∵,∴OE=DF=a,DE∥OG,
∵OA=a,
∴AE=OE=,
∴DE是△AOG的中位线,
∴AD=DG,
∴AD=OD=DG,
∴∠DOG=∠DGO,
∵∠ADO=∠ABO,∠AHD=∠OHB,
∴∠DAB=∠DOG,
∴∠BAD=∠BGD,
∴AB=BG,
∵DO=DG,DF⊥x轴,
∴OG=2OF=2c,
又∵OG=OB+BG=b+AB=2c,
∴AB=2c-b;
(3)连接OE,作EG⊥DB于G,EH⊥x轴于H,如图,
∵EA=ED,OA=OD=a,OE=OE,
∴△AOE≌△DOE,
∴∠AOE=∠DOE=45°,
∴OE平分∠AOD,
∵,
∴F在∠AOD的平分线上,
∴O、E、F三点共线,
设E(n,n),则,
∵ED=EB,EG⊥DB,
∴DG=BG,即n-a=b-n,可得,
在Rt△BEG中,由勾股定理得,
∵,
∴,
∴,
∴
