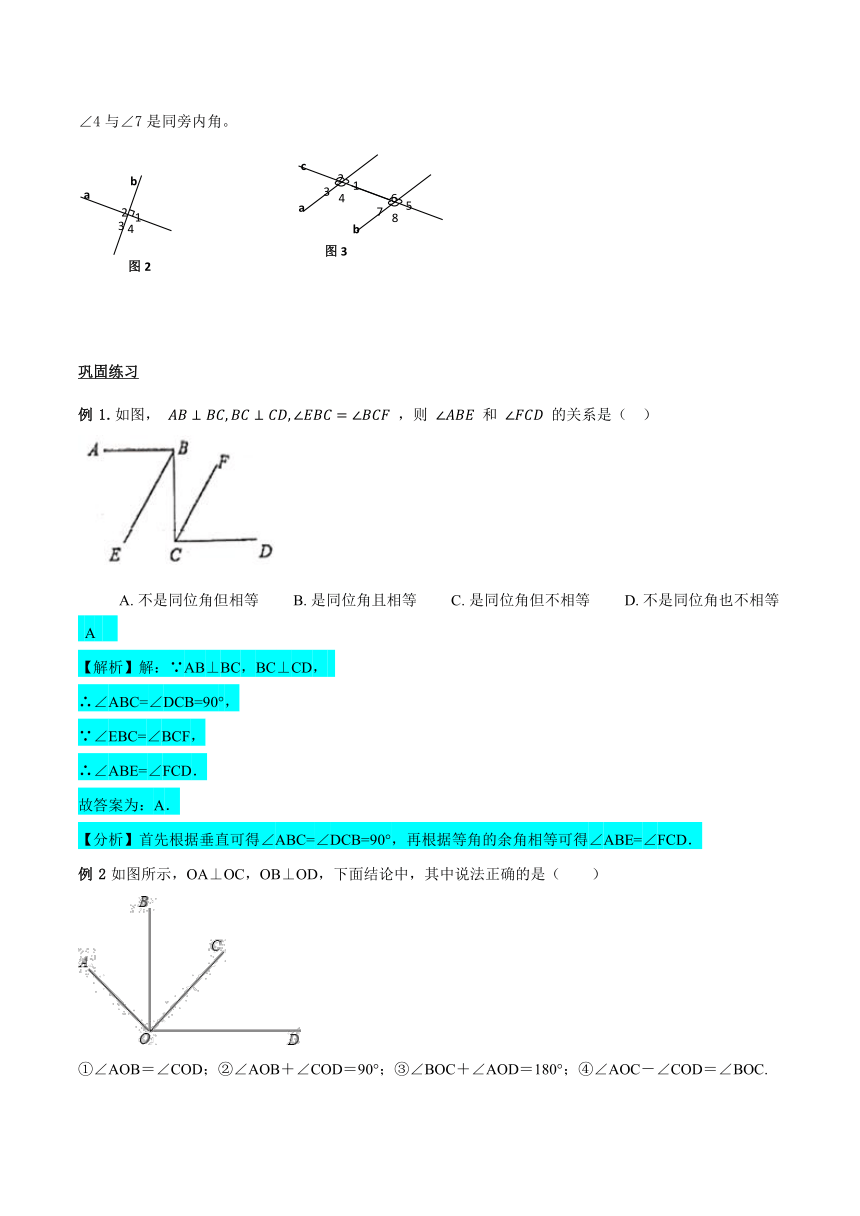
5.1相交线-2020-2021学年人教版七年级数学下册学案
文档属性
| 名称 | 5.1相交线-2020-2021学年人教版七年级数学下册学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 57.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 20:57:00 | ||
图片预览


文档简介
初中数学七年级下册第五章相交线与平行线学案(人教版)
5.1相交线
学习目标
1.研究邻补角和对顶角的概念,对顶角的性质
2.理解垂线的定义,点到直线的距离,掌握垂线的性质,会过一点画已知直线的垂线
3.掌握用三角板或量角器过一点画已知直线的垂线
4.理解同位角、内错角、同旁内角的定义
5.识别图中同位角、内错角、同旁内角
新知形成
知识点一、邻补角
两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
邻补角的性质:邻补角互补
。
如图1所示,
∠1
与∠2、
∠4互为邻补角,∠3与∠2、∠4互为邻补角。∠1
+
∠4
=
180°;∠1
+∠2
=
180°
;∠3+∠2
=
180°;∠3+∠4
=
180°。
知识点二、对顶角
两条直线相交所构成的四个角中,一个角的两边分别是另一个角的两边的
反向延长线
,这样的两个角互为
对顶角
。对顶角的性质:对顶角相等。如图1所示,∠1与
∠3、∠2与∠4互为对顶角。∠1=∠3;∠2=∠4。
知识点三、垂线
垂线两条直线相交所成的角中,如果有一个是直角或90°时,称这两条直线互相垂直,其中一条叫做另一条的垂线。
如图2所示,当∠1=
90°时,
a⊥b。
垂线的性质:
性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
性质3:如图2所示,当
a
⊥
b
时,∠1=
∠2
=∠3
=∠4=
90°。
点到直线的距离:直线外一点到这条直线的垂线段的长度叫点到直线的距离。
知识点四、同位角、内错角、同旁内角
①在两条直线(被截线)的
同一方
,都在第三条直线(截线)的
同一侧
,这样
的两个角叫
同位角
。图3中,共有4对同位角:∠1与∠5是同位角;
∠2与∠6是同位角;∠3与∠7是同位角;∠4与∠8是同位角。
②在两条直线(被截线)
之间
,并且在第三条直线(截线)的
两侧
,这样的两个角叫
内错角
。图3中,共有2对内错角:∠1与∠7是内错角;∠4与∠6是内错角。
③在两条直线(被截线)的
之间
,都在第三条直线(截线)的
同一旁
,这样的两个角叫
同旁内角
。图3中,共有2对同旁内角:∠1与∠6是同旁内角;
∠4与∠7是同旁内角。
巩固练习
例1.如图,
,则
和
的关系是(??
)
A.?不是同位角但相等?????????B.?是同位角且相等?????????C.?是同位角但不相等?????????D.?不是同位角也不相等
A
【解析】解:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
∵∠EBC=∠BCF,
∴∠ABE=∠FCD.
故答案为:A.
【分析】首先根据垂直可得∠ABC=∠DCB=90°,再根据等角的余角相等可得∠ABE=∠FCD.
例2如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.?①②③????????????????????????????????B.?①②④????????????????????????????????C.?①③④????????????????????????????????D.?②③④
C
【解析】由题意可知,OA⊥OC,所以∠AOC=90°,即∠AOB+∠BOC=90°.同时,OB⊥OD,所以∠BOD=90°,即∠COD+∠BOC=90°.依次,可以判定∠AOB=∠COD,所以①正确.又因为不能推断出∠AOB与∠COD的具体角度,所以②不正确.∠AOD=∠AOB+∠BOC+∠COD,所以∠BOC+∠AOD=∠BOC+∠AOB+∠BOC+∠COD=90°+90°=180°.因为∠AOB=∠COD,所以∠AOC-∠COD=∠AOC-∠AOB=∠BOC,所以④正确.为此,选C.
【分析】在掌握两直线相互垂直,夹角为直角的基础上,学会角度转换,就能轻松找到正确答案.本题考查垂线.
课后作业
1.若线段
,
分别是
边上的高线和中线,则(??
)
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
2.下列说法中,错误的有(???
)
A.?过两点有且只有一条直线????????????????????????????????B.?直线外一点到这条线段的垂线段叫点到直线的距离
C.?两点之间,线段最短???????????????????????????????????????D.?垂线段最短
3.两条直线相交所成的四个角分别满足下列条件之一,其中不能判定这两条直线垂直的条件是(???
)
A.?两对对顶角分别相等??????????B.?有一对对顶角互补??????????C.?有一对邻补角相等??????????D.?有三个角相等
4.点A为直线a外一点,点B是直线
a上一点,点
A到直线a的距离为5cm,则AB的长
度可能为(?
)
A.?2cm????????????????????????????????????B.?3cm????????????????????????????????????C.?4cm????????????????????????????????????D.?18cm
5.如图,OA⊥OB,若∠1=40°,则∠2的度数是
A.?20°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
6.如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是(??
?)
A.?2.5??????????????????????????????????????????B.?3??????????????????????????????????????????C.?4??????????????????????????????????????????D.?5
7.如图,AD⊥AC交BC的延长线于点D,AE⊥BC
交BC的延长线于点
E,CF⊥AB
于点F,则图中能表示点A到直线BC的距离的是(???
)
A.?AD
的长度?????????????????????????B.?AE
的长度?????????????????????????C.?AC
的长度?????????????????????????D.?CF
的长度
8.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有(?
)
A.?①????????????????????????????????????B.?①②③????????????????????????????????????C.?①④????????????????????????????????????D.?②③④
9.在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为(???
)
A.?20°????????????????????????????????B.?55°????????????????????????????????C.?20°或
125°????????????????????????????????D.?20°或55°
10.如图,直线AB,CD相交于点O,下列条件中:①∠AOD=90°
;②∠AOD=∠AOC;③∠AOC+∠BOC=180°;④∠AOC+∠BOD=180°,能说明AB⊥CD的有(??
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
参考答案
1.
D
2.
B
3.
A
4.
D
5.
C
6.
A
7.
B
8.
C
9.
C
10.
C
5.1相交线
学习目标
1.研究邻补角和对顶角的概念,对顶角的性质
2.理解垂线的定义,点到直线的距离,掌握垂线的性质,会过一点画已知直线的垂线
3.掌握用三角板或量角器过一点画已知直线的垂线
4.理解同位角、内错角、同旁内角的定义
5.识别图中同位角、内错角、同旁内角
新知形成
知识点一、邻补角
两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
邻补角的性质:邻补角互补
。
如图1所示,
∠1
与∠2、
∠4互为邻补角,∠3与∠2、∠4互为邻补角。∠1
+
∠4
=
180°;∠1
+∠2
=
180°
;∠3+∠2
=
180°;∠3+∠4
=
180°。
知识点二、对顶角
两条直线相交所构成的四个角中,一个角的两边分别是另一个角的两边的
反向延长线
,这样的两个角互为
对顶角
。对顶角的性质:对顶角相等。如图1所示,∠1与
∠3、∠2与∠4互为对顶角。∠1=∠3;∠2=∠4。
知识点三、垂线
垂线两条直线相交所成的角中,如果有一个是直角或90°时,称这两条直线互相垂直,其中一条叫做另一条的垂线。
如图2所示,当∠1=
90°时,
a⊥b。
垂线的性质:
性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
性质3:如图2所示,当
a
⊥
b
时,∠1=
∠2
=∠3
=∠4=
90°。
点到直线的距离:直线外一点到这条直线的垂线段的长度叫点到直线的距离。
知识点四、同位角、内错角、同旁内角
①在两条直线(被截线)的
同一方
,都在第三条直线(截线)的
同一侧
,这样
的两个角叫
同位角
。图3中,共有4对同位角:∠1与∠5是同位角;
∠2与∠6是同位角;∠3与∠7是同位角;∠4与∠8是同位角。
②在两条直线(被截线)
之间
,并且在第三条直线(截线)的
两侧
,这样的两个角叫
内错角
。图3中,共有2对内错角:∠1与∠7是内错角;∠4与∠6是内错角。
③在两条直线(被截线)的
之间
,都在第三条直线(截线)的
同一旁
,这样的两个角叫
同旁内角
。图3中,共有2对同旁内角:∠1与∠6是同旁内角;
∠4与∠7是同旁内角。
巩固练习
例1.如图,
,则
和
的关系是(??
)
A.?不是同位角但相等?????????B.?是同位角且相等?????????C.?是同位角但不相等?????????D.?不是同位角也不相等
A
【解析】解:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
∵∠EBC=∠BCF,
∴∠ABE=∠FCD.
故答案为:A.
【分析】首先根据垂直可得∠ABC=∠DCB=90°,再根据等角的余角相等可得∠ABE=∠FCD.
例2如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.?①②③????????????????????????????????B.?①②④????????????????????????????????C.?①③④????????????????????????????????D.?②③④
C
【解析】由题意可知,OA⊥OC,所以∠AOC=90°,即∠AOB+∠BOC=90°.同时,OB⊥OD,所以∠BOD=90°,即∠COD+∠BOC=90°.依次,可以判定∠AOB=∠COD,所以①正确.又因为不能推断出∠AOB与∠COD的具体角度,所以②不正确.∠AOD=∠AOB+∠BOC+∠COD,所以∠BOC+∠AOD=∠BOC+∠AOB+∠BOC+∠COD=90°+90°=180°.因为∠AOB=∠COD,所以∠AOC-∠COD=∠AOC-∠AOB=∠BOC,所以④正确.为此,选C.
【分析】在掌握两直线相互垂直,夹角为直角的基础上,学会角度转换,就能轻松找到正确答案.本题考查垂线.
课后作业
1.若线段
,
分别是
边上的高线和中线,则(??
)
A.?????????????????????????B.?????????????????????????C.?????????????????????????D.?
2.下列说法中,错误的有(???
)
A.?过两点有且只有一条直线????????????????????????????????B.?直线外一点到这条线段的垂线段叫点到直线的距离
C.?两点之间,线段最短???????????????????????????????????????D.?垂线段最短
3.两条直线相交所成的四个角分别满足下列条件之一,其中不能判定这两条直线垂直的条件是(???
)
A.?两对对顶角分别相等??????????B.?有一对对顶角互补??????????C.?有一对邻补角相等??????????D.?有三个角相等
4.点A为直线a外一点,点B是直线
a上一点,点
A到直线a的距离为5cm,则AB的长
度可能为(?
)
A.?2cm????????????????????????????????????B.?3cm????????????????????????????????????C.?4cm????????????????????????????????????D.?18cm
5.如图,OA⊥OB,若∠1=40°,则∠2的度数是
A.?20°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
6.如图,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP长不可能是(??
?)
A.?2.5??????????????????????????????????????????B.?3??????????????????????????????????????????C.?4??????????????????????????????????????????D.?5
7.如图,AD⊥AC交BC的延长线于点D,AE⊥BC
交BC的延长线于点
E,CF⊥AB
于点F,则图中能表示点A到直线BC的距离的是(???
)
A.?AD
的长度?????????????????????????B.?AE
的长度?????????????????????????C.?AC
的长度?????????????????????????D.?CF
的长度
8.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有(?
)
A.?①????????????????????????????????????B.?①②③????????????????????????????????????C.?①④????????????????????????????????????D.?②③④
9.在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为(???
)
A.?20°????????????????????????????????B.?55°????????????????????????????????C.?20°或
125°????????????????????????????????D.?20°或55°
10.如图,直线AB,CD相交于点O,下列条件中:①∠AOD=90°
;②∠AOD=∠AOC;③∠AOC+∠BOC=180°;④∠AOC+∠BOD=180°,能说明AB⊥CD的有(??
)
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
参考答案
1.
D
2.
B
3.
A
4.
D
5.
C
6.
A
7.
B
8.
C
9.
C
10.
C
