2020-2021学年人教版七年级数学下册5.4平移导学案
文档属性
| 名称 | 2020-2021学年人教版七年级数学下册5.4平移导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 488.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 00:00:00 | ||
图片预览


文档简介
5.4平移
【总结解题方法
提升解题能力】
【知识点梳理】1、定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移.【要点诠释】(1)图形的平移的两要素:平移的方向与平移的距离.(2)图形的平移不改变图形的形状与大小,只改变图形的位置.2、性质:图形的平移实质上是将图形上所有点沿同一方向移动相同的距离,平移不改变线段、角的大小,具体来说:(1)平移后,对应线段平行且相等;(2)平移后,对应角相等;(3)平移后,对应点所连线段平行且相等;(4)平移后,新图形与原图形是一对全等图形.【要点诠释】(1)“连接各组对应点的线段”的线段的长度实际上就是平移的距离.(2)要注意“连接各组对应点的线段”与“对应线段”的区别,前者是通过连接平移前后的对应点得到的,而后者是原来的图形与平移后的图形上本身存在的.3、作图:平移作图是平移基本性质的应用,在具体作图时,应抓住作图的“四步曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺次连接对应点.
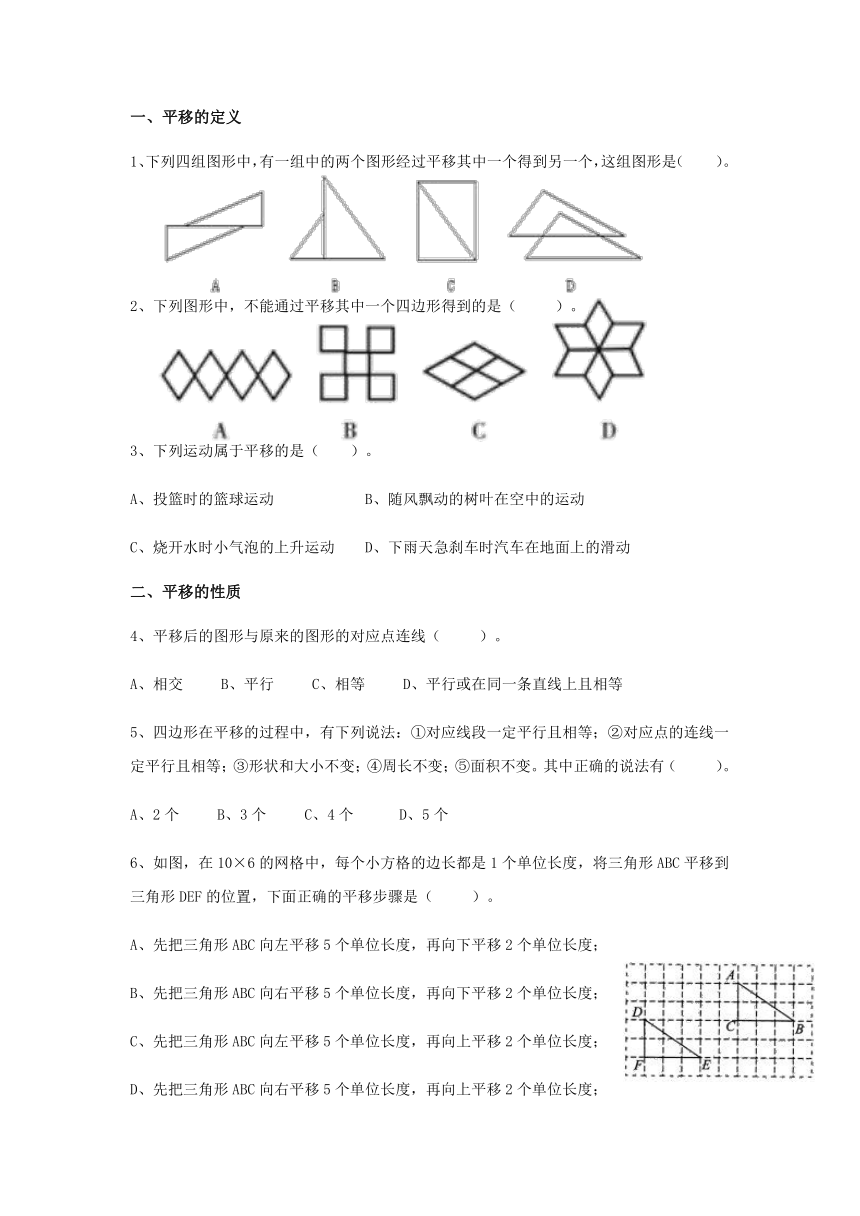
一、平移的定义
1、下列四组图形中,有一组中的两个图形经过平移其中一个得到另一个,这组图形是(
)。
2、下列图形中,不能通过平移其中一个四边形得到的是(
)。
3、下列运动属于平移的是(
)。
A、投篮时的篮球运动
B、随风飘动的树叶在空中的运动
C、烧开水时小气泡的上升运动
D、下雨天急刹车时汽车在地面上的滑动
二、平移的性质
4、平移后的图形与原来的图形的对应点连线(
)。
A、相交
B、平行
C、相等
D、平行或在同一条直线上且相等
5、四边形在平移的过程中,有下列说法:①对应线段一定平行且相等;②对应点的连线一定平行且相等;③形状和大小不变;④周长不变;⑤面积不变。其中正确的说法有(
)。
A、2个
B、3个
C、4个
D、5个
6、如图,在10×6的网格中,每个小方格的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是(
)。
A、先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度;
B、先把三角形ABC向右平移5个单位长度,再向下平移2个单位长度;
C、先把三角形ABC向左平移5个单位长度,再向上平移2个单位长度;
D、先把三角形ABC向右平移5个单位长度,再向上平移2个单位长度;
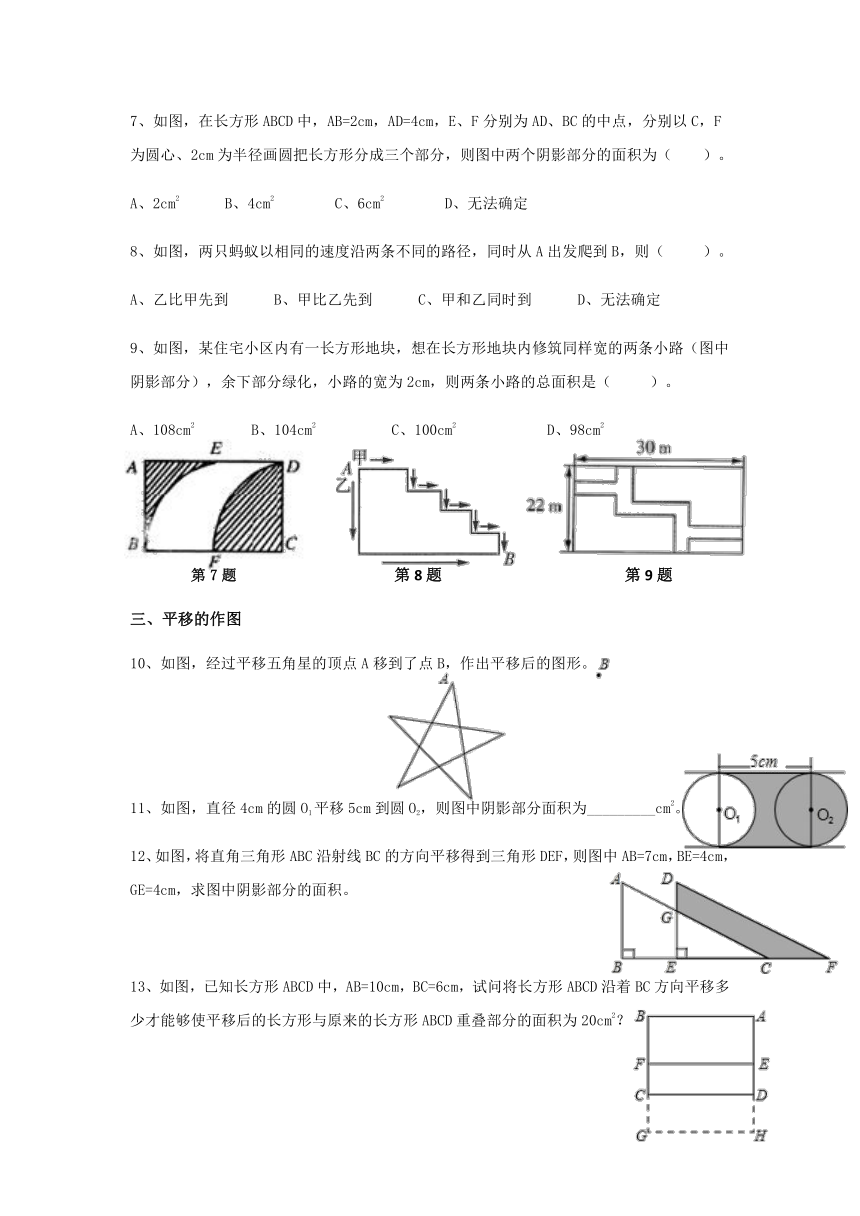
7、如图,在长方形ABCD中,AB=2cm,AD=4cm,E、F分别为AD、BC的中点,分别以C,F为圆心、2cm为半径画圆把长方形分成三个部分,则图中两个阴影部分的面积为(
)。
A、2cm2
B、4cm2
C、6cm2
D、无法确定
8、如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则(
)。
A、乙比甲先到
B、甲比乙先到
C、甲和乙同时到
D、无法确定
9、如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2cm,则两条小路的总面积是(
)。
A、108cm2
B、104cm2
C、100cm2
D、98cm2
第7题
第8题
第9题
三、平移的作图
10、如图,经过平移五角星的顶点A移到了点B,作出平移后的图形。
11、如图,直径4cm的圆O1平移5cm到圆O2,则图中阴影部分面积为_________cm2。
12、如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF,则图中AB=7cm,BE=4cm,GE=4cm,求图中阴影部分的面积。
13、如图,已知长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着BC方向平移多少才能够使平移后的长方形与原来的长方形ABCD重叠部分的面积为20cm2?
【巩固练习】
一、选择题。
1、下列现象中不属于平移的是(
)。
A、滑雪运动员在平坦的雪地上滑雪
B、彩票大转盘在旋转
C、高楼的电梯在上上下下
D、火车在一段笔直的铁轨上行驶
2、如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有(
)。
A、0条
B、1条
C、2条
D、3条
3、如图所示,在一个由4×4个小正方形组成的正方形网格中,把线段EF向右平移3个单位,向下平移1个单位得到线段GH,则阴影部分面积与正方形ABCD的面积比是(
)。
A、3:4
B、5:8
C、9:16
D、1:2
4、如图,将△ABE向右平移得到△DCF,与交于点,其中,,则(
)。
A、
B、
C、
D、
5、如图,将△ABE向右平移2
cm得到△DCF,如果△ABE的周长是16
cm,那么四边形ABFD的周长是(
)。
A、16
cm
B、18
cm
C、20
cm
D、21
cm
二、填空题。
6、如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'=
_________.
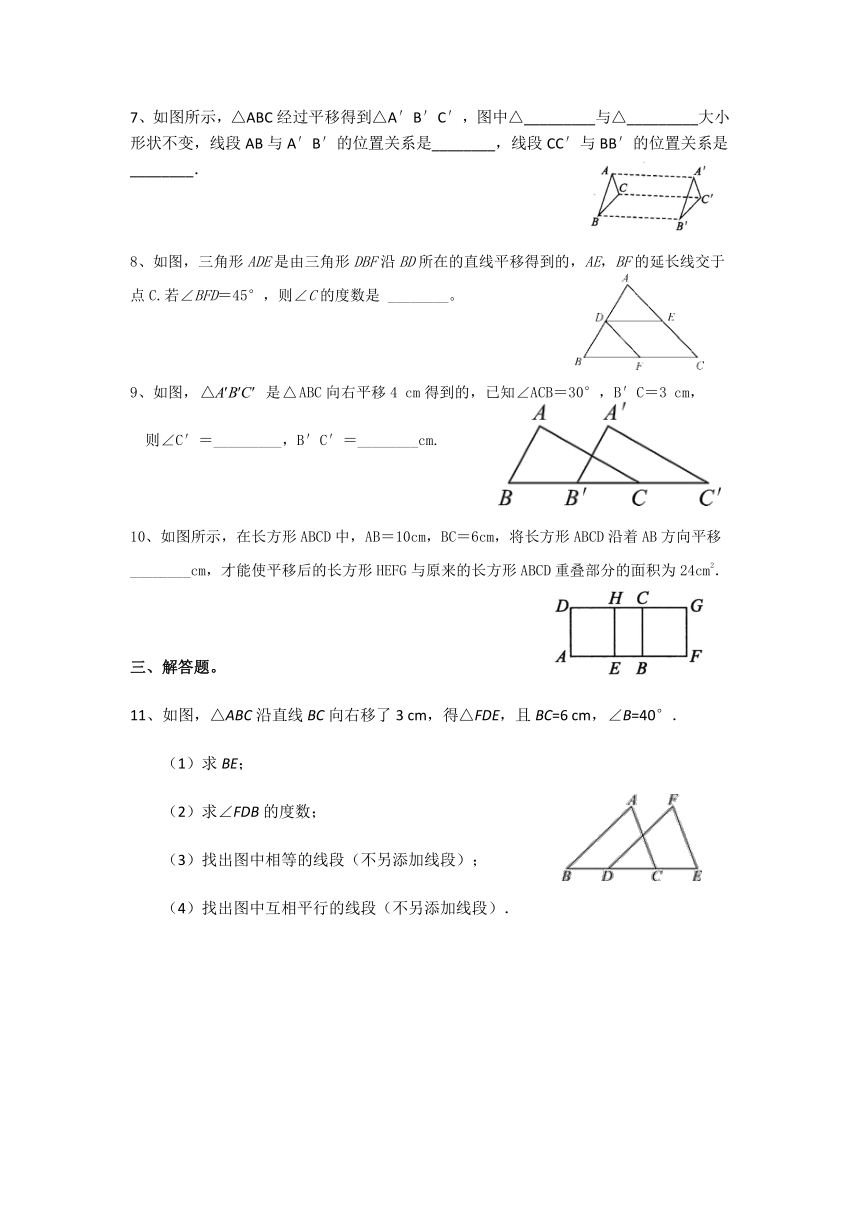
7、如图所示,△ABC经过平移得到△A′B′C′,图中△_________与△_________大小形状不变,线段AB与A′B′的位置关系是________,线段CC′与BB′的位置关系是________.
8、如图,三角形ADE是由三角形DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=45°,则∠C的度数是
________。
9、如图,
是ABC向右平移4
cm得到的,已知∠ACB=30°,B′C=3
cm,
则∠C′=_________,B′C′=________cm.
10、如图所示,在长方形ABCD中,AB=10cm,BC=6cm,将长方形ABCD沿着AB方向平移________cm,才能使平移后的长方形HEFG与原来的长方形ABCD重叠部分的面积为24cm2.
三、解答题。
11、如图,△ABC沿直线BC向右移了3
cm,得△FDE,且BC=6
cm,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
12、如图,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置,并作出△DEF.
13、如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)直接写出点C1的坐标;(2)求△AOA1的面积.
14、如图是一块长方形的草地,
长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
15、如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼梯宽为2
m,其侧面与正面如图所示,则购买地毯至少需要多少元?
答
案
一、平移的定义
1、下列四组图形中,有一组中的两个图形经过平移其中一个得到另一个,这组图形是(
)。
【答案】D
【解析】A对应点的连线相交,B形状不同,C对应点的连线相交,不能通过平移得到,与题不符;D能通过平移得到,与题意相符;故选D。
2、下列图形中,不能通过平移其中一个四边形得到的是(
)。
【答案】D
【解析】A、B、C能通过其中一个四边形平移得到,不符合题意;D不能通过其中一个四边形平移得到,需要一个四边形旋转得到,符合题意;故选D。
3、下列运动属于平移的是(
)。
A、投篮时的篮球运动
B、随风飘动的树叶在空中的运动
C、烧开水时小气泡的上升运动
D、下雨天急刹车时汽车在地面上的滑动
【答案】D
【解析】A投篮时的篮球不沿直线运动,故错误;B随风飘动的树叶在空中不沿直线运动,故错误;C开水时小气泡的上升,有大小变化,不符合平移定义,故错误;D下雨天急刹车时汽车在地面上的滑动是平移,故选D
二、平移的性质
4、平移后的图形与原来的图形的对应点连线(
D
)。
A、相交
B、平行
C、相等
D、平行或在同一条直线上且相等
5、四边形在平移的过程中,有下列说法:①对应线段一定平行且相等;②对应点的连线一定平行且相等;③形状和大小不变;④周长不变;⑤面积不变。其中正确的说法有(
)。
A、2个
B、3个
C、4个
D、5个
【答案】B
【解析】①对应线段一定相等,不一定平行(可能共线);②可能共线;③④⑤正确,平移只改变位置,不改变形状大小,故对应的周长和面积平移前后不变,故正确选③④⑤,共3个。
6、如图,在10×6的网格中,每个小方格的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是(
)。
A、先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度;
B、先把三角形ABC向右平移5个单位长度,再向下平移2个单位长度;
C、先把三角形ABC向左平移5个单位长度,再向上平移2个单位长度;
D、先把三角形ABC向右平移5个单位长度,再向上平移2个单位长度;
【答案】A
【解析】观察对应点A、D,可知点A向左平移5个单位长度,再向下平移2个单位长度即可到达点D的位置,所以平移的步骤是先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度,故选A。
7、如图,在长方形ABCD中,AB=2cm,AD=4cm,E、F分别为AD、BC的中点,分别以C,F为圆心、2cm为半径画圆把长方形分成三个部分,则图中两个阴影部分的面积为(
)。
A、2cm2
B、4cm2
C、6cm2
D、无法确定
【答案】B
【解析】阴影部分面积=长方形面积的一半
故阴影部分面积=2×2=4cm2
,故选B。
8、如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则(
)。
A、乙比甲先到
B、甲比乙先到
C、甲和乙同时到
D、无法确定
【答案】C
【解析】因为甲、乙两只蚂蚁的行程相同,速度相同,所以甲、乙两只蚂蚁同时到达。故选C。
9、如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2cm,则两条小路的总面积是(
)。
A、108cm2
B、104cm2
C、100cm2
D、98cm2
【答案】
C
【解析】利用平移可得,两条小路的总面积是:
30×22—(30—2)×(22—2)=100cm2,故选C。
三、平移的作图
10、如图,经过平移五角星的顶点A移到了点B,作出平移后的图形。
【答案】
11、如图,直径4cm的圆O1平移5cm到圆O2,则图中阴影部分面积为__20___cm2。
【答案】∵圆O1平移5cm到圆O2,∴圆O1与圆O2全等,
∴图中的阴影部分的面积=图中的矩形的面积
∴4×5=20cm2,∴图中阴影部分面积为20cm2.
12、如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF,则图中AB=7cm,BE=4cm,GE=4cm,求图中阴影部分的面积。
【答案】∵▲ABC沿射线BC的方向平移得到▲DEF;
∴▲ABC与▲DEF全等;
∴阴影部分的面积=梯形ABEG的面积;
∴阴影部分面积=×(7+4)×4=22cm2.
13、如图,已知长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着BC方向平移多少才能够使平移后的长方形与原来的长方形ABCD重叠部分的面积为20cm2?
【答案】解:设AE=X,根据题意列出方程:
10(6—X)=20,解得X=4
∵A的对应点为E,∴平移距离为AE的长,故向下平移4cm.
【巩固练习】
一、选择题。
1、下列现象中不属于平移的是(
)。
A、滑雪运动员在平坦的雪地上滑雪
B、彩票大转盘在旋转
C、高楼的电梯在上上下下
D、火车在一段笔直的铁轨上行驶
【答案】B
【解析】A滑雪运动员在平坦的雪地上滑雪,
属于平移,故本选项错误;B彩票大转盘在旋转,不属于平移,故本选项正确;C
高楼的电梯在上上下下,
属于平移,
故本选项错误;D
火车在一段笔直的铁轨上行驶,
属于平移,故本选项错误.故选:B.
2、如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有(
)。
A、0条
B、1条
C、2条
D、3条
3、如图所示,在一个由4×4个小正方形组成的正方形网格中,把线段EF向右平移3个单位,向下平移1个单位得到线段GH,则阴影部分面积与正方形ABCD的面积比是(
)。
A、3:4
B、5:8
C、9:16
D、1:2
【答案】B;
【解析】,,所以.
4、如图,将△ABE向右平移得到△DCF,与交于点,其中,,则(
)。
A、
B、
C、
D、
【答案】B
【解析】∵△ABE向右平移得到△DCF,∴AB∥CD,AE∥DF,∴∠DCF=∠B=45°,
∴∠CDF=180°-45°-60°=75°,∴∠AGC=∠DGE=180°-75°=105°,故选B.
5、如图,将△ABE向右平移2
cm得到△DCF,如果△ABE的周长是16
cm,那么四边形ABFD的周长是(
)。
A、16
cm
B、18
cm
C、20
cm
D、21
cm
【答案】C
【解析】已知,△ABE向右平移2
cm得到△DCF,根据平移的性质得到EF=AD=2
cm,AE=DF,又因△ABE的周长为16
cm,所以AB+BE+AE=16
cm,则四边形ABFD的周长=AB+BC+CF+DF+AD=16+2+2=20(cm),故选C.
二、填空题。
6、如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'=
_________.
【答案】5
【解析】∵把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,∴三角板向右平移了5个单位,∴顶点C平移的距离CC′=5.故答案为:5.
7、如图所示,△ABC经过平移得到△A′B′C′,图中△_________与△_________大小形状不变,线段AB与A′B′的位置关系是________,线段CC′与BB′的位置关系是________.
【答案】ABC,
A′B′C′,平行,平行;
【解析】平移的性质.
8、如图,三角形ADE是由三角形DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=45°,则∠C的度数是
________。
【答案】45°;【解析】∵△ADE是由△DBF沿BD所在的直线平移得到的,
∴DE∥BC,∠BFD=∠AED,∴∠AED=∠C∴∠C=∠BFD=45°.故答案是:45°.
9、如图,
是ABC向右平移4
cm得到的,已知∠ACB=30°,B′C=3
cm,则∠C′=_________,B′C′=________cm.
【答案】30°,7
【解析】∵
是ABC向右平移4
cm得到的,∴BB′=CC′=4
cm,
∠C′=∠ACB=30°,∵B′C=3
cm,∴B′C′=4+3=7
cm.故答案为:30°,7.
10、如图所示,在长方形ABCD中,AB=10cm,BC=6cm,将长方形ABCD沿着AB方向平移________cm,才能使平移后的长方形HEFG与原来的长方形ABCD重叠部分的面积为24cm2.
【答案】6;
【解析】重叠部分长方形的一边长为6cm,另一边长为:24÷6=4
cm,
所以平移的距离为:AE=10-4=6
cm.
三、解答题。
11、如图,△ABC沿直线BC向右移了3
cm,得△FDE,且BC=6
cm,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
12、如图,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置,并作出△DEF.
【解析】如图:
13、如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)直接写出点C1的坐标;(2)求△AOA1的面积.
【答案】(1)、(4,﹣2);(2)、6.
【解析】(1)、根据点P的对应点坐标得出平移的法则,从而得出点C1的坐标;
(2)、利用矩形的面积减去三个直角三角形的面积得出答案.
【解答】(1)、∵点P(a,b)的对应点为P1(a+6,b﹣2),
∴平移规律为向右6个单位,向下2个单位,
∴C(﹣2,0)的对应点C1的坐标为(4,﹣2);
(2)、△AOA1的面积:6×3﹣×3×3﹣×3×1﹣×6×2=6.
14、如图是一块长方形的草地,
长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
【解析】如图,过小路出口的一个端点作垂线,将垂线左边的图形
平移至小路右边,可得该图形的一个宽为1m,长为15m的小长方形。
故长草部分的面积为:(21—1)×15=300(m2)
15、如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼梯宽为2
m,其侧面与正面如图所示,则购买地毯至少需要多少元?
【解析】利用平移线段,把楼梯的横竖向上向左平移,
构成一个长方形,长、宽分别为5米,3米,∴地毯的长度为5+3=8(米),
∴地毯的面积为8×2=16(平方米),
∴买地毯至少需要16×32=512(元).
【总结解题方法
提升解题能力】
【知识点梳理】1、定义:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种移动叫做平移.【要点诠释】(1)图形的平移的两要素:平移的方向与平移的距离.(2)图形的平移不改变图形的形状与大小,只改变图形的位置.2、性质:图形的平移实质上是将图形上所有点沿同一方向移动相同的距离,平移不改变线段、角的大小,具体来说:(1)平移后,对应线段平行且相等;(2)平移后,对应角相等;(3)平移后,对应点所连线段平行且相等;(4)平移后,新图形与原图形是一对全等图形.【要点诠释】(1)“连接各组对应点的线段”的线段的长度实际上就是平移的距离.(2)要注意“连接各组对应点的线段”与“对应线段”的区别,前者是通过连接平移前后的对应点得到的,而后者是原来的图形与平移后的图形上本身存在的.3、作图:平移作图是平移基本性质的应用,在具体作图时,应抓住作图的“四步曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点;
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图形顺次连接对应点.
一、平移的定义
1、下列四组图形中,有一组中的两个图形经过平移其中一个得到另一个,这组图形是(
)。
2、下列图形中,不能通过平移其中一个四边形得到的是(
)。
3、下列运动属于平移的是(
)。
A、投篮时的篮球运动
B、随风飘动的树叶在空中的运动
C、烧开水时小气泡的上升运动
D、下雨天急刹车时汽车在地面上的滑动
二、平移的性质
4、平移后的图形与原来的图形的对应点连线(
)。
A、相交
B、平行
C、相等
D、平行或在同一条直线上且相等
5、四边形在平移的过程中,有下列说法:①对应线段一定平行且相等;②对应点的连线一定平行且相等;③形状和大小不变;④周长不变;⑤面积不变。其中正确的说法有(
)。
A、2个
B、3个
C、4个
D、5个
6、如图,在10×6的网格中,每个小方格的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是(
)。
A、先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度;
B、先把三角形ABC向右平移5个单位长度,再向下平移2个单位长度;
C、先把三角形ABC向左平移5个单位长度,再向上平移2个单位长度;
D、先把三角形ABC向右平移5个单位长度,再向上平移2个单位长度;
7、如图,在长方形ABCD中,AB=2cm,AD=4cm,E、F分别为AD、BC的中点,分别以C,F为圆心、2cm为半径画圆把长方形分成三个部分,则图中两个阴影部分的面积为(
)。
A、2cm2
B、4cm2
C、6cm2
D、无法确定
8、如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则(
)。
A、乙比甲先到
B、甲比乙先到
C、甲和乙同时到
D、无法确定
9、如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2cm,则两条小路的总面积是(
)。
A、108cm2
B、104cm2
C、100cm2
D、98cm2
第7题
第8题
第9题
三、平移的作图
10、如图,经过平移五角星的顶点A移到了点B,作出平移后的图形。
11、如图,直径4cm的圆O1平移5cm到圆O2,则图中阴影部分面积为_________cm2。
12、如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF,则图中AB=7cm,BE=4cm,GE=4cm,求图中阴影部分的面积。
13、如图,已知长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着BC方向平移多少才能够使平移后的长方形与原来的长方形ABCD重叠部分的面积为20cm2?
【巩固练习】
一、选择题。
1、下列现象中不属于平移的是(
)。
A、滑雪运动员在平坦的雪地上滑雪
B、彩票大转盘在旋转
C、高楼的电梯在上上下下
D、火车在一段笔直的铁轨上行驶
2、如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有(
)。
A、0条
B、1条
C、2条
D、3条
3、如图所示,在一个由4×4个小正方形组成的正方形网格中,把线段EF向右平移3个单位,向下平移1个单位得到线段GH,则阴影部分面积与正方形ABCD的面积比是(
)。
A、3:4
B、5:8
C、9:16
D、1:2
4、如图,将△ABE向右平移得到△DCF,与交于点,其中,,则(
)。
A、
B、
C、
D、
5、如图,将△ABE向右平移2
cm得到△DCF,如果△ABE的周长是16
cm,那么四边形ABFD的周长是(
)。
A、16
cm
B、18
cm
C、20
cm
D、21
cm
二、填空题。
6、如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'=
_________.
7、如图所示,△ABC经过平移得到△A′B′C′,图中△_________与△_________大小形状不变,线段AB与A′B′的位置关系是________,线段CC′与BB′的位置关系是________.
8、如图,三角形ADE是由三角形DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=45°,则∠C的度数是
________。
9、如图,
是ABC向右平移4
cm得到的,已知∠ACB=30°,B′C=3
cm,
则∠C′=_________,B′C′=________cm.
10、如图所示,在长方形ABCD中,AB=10cm,BC=6cm,将长方形ABCD沿着AB方向平移________cm,才能使平移后的长方形HEFG与原来的长方形ABCD重叠部分的面积为24cm2.
三、解答题。
11、如图,△ABC沿直线BC向右移了3
cm,得△FDE,且BC=6
cm,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
12、如图,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置,并作出△DEF.
13、如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)直接写出点C1的坐标;(2)求△AOA1的面积.
14、如图是一块长方形的草地,
长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
15、如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼梯宽为2
m,其侧面与正面如图所示,则购买地毯至少需要多少元?
答
案
一、平移的定义
1、下列四组图形中,有一组中的两个图形经过平移其中一个得到另一个,这组图形是(
)。
【答案】D
【解析】A对应点的连线相交,B形状不同,C对应点的连线相交,不能通过平移得到,与题不符;D能通过平移得到,与题意相符;故选D。
2、下列图形中,不能通过平移其中一个四边形得到的是(
)。
【答案】D
【解析】A、B、C能通过其中一个四边形平移得到,不符合题意;D不能通过其中一个四边形平移得到,需要一个四边形旋转得到,符合题意;故选D。
3、下列运动属于平移的是(
)。
A、投篮时的篮球运动
B、随风飘动的树叶在空中的运动
C、烧开水时小气泡的上升运动
D、下雨天急刹车时汽车在地面上的滑动
【答案】D
【解析】A投篮时的篮球不沿直线运动,故错误;B随风飘动的树叶在空中不沿直线运动,故错误;C开水时小气泡的上升,有大小变化,不符合平移定义,故错误;D下雨天急刹车时汽车在地面上的滑动是平移,故选D
二、平移的性质
4、平移后的图形与原来的图形的对应点连线(
D
)。
A、相交
B、平行
C、相等
D、平行或在同一条直线上且相等
5、四边形在平移的过程中,有下列说法:①对应线段一定平行且相等;②对应点的连线一定平行且相等;③形状和大小不变;④周长不变;⑤面积不变。其中正确的说法有(
)。
A、2个
B、3个
C、4个
D、5个
【答案】B
【解析】①对应线段一定相等,不一定平行(可能共线);②可能共线;③④⑤正确,平移只改变位置,不改变形状大小,故对应的周长和面积平移前后不变,故正确选③④⑤,共3个。
6、如图,在10×6的网格中,每个小方格的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是(
)。
A、先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度;
B、先把三角形ABC向右平移5个单位长度,再向下平移2个单位长度;
C、先把三角形ABC向左平移5个单位长度,再向上平移2个单位长度;
D、先把三角形ABC向右平移5个单位长度,再向上平移2个单位长度;
【答案】A
【解析】观察对应点A、D,可知点A向左平移5个单位长度,再向下平移2个单位长度即可到达点D的位置,所以平移的步骤是先把三角形ABC向左平移5个单位长度,再向下平移2个单位长度,故选A。
7、如图,在长方形ABCD中,AB=2cm,AD=4cm,E、F分别为AD、BC的中点,分别以C,F为圆心、2cm为半径画圆把长方形分成三个部分,则图中两个阴影部分的面积为(
)。
A、2cm2
B、4cm2
C、6cm2
D、无法确定
【答案】B
【解析】阴影部分面积=长方形面积的一半
故阴影部分面积=2×2=4cm2
,故选B。
8、如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则(
)。
A、乙比甲先到
B、甲比乙先到
C、甲和乙同时到
D、无法确定
【答案】C
【解析】因为甲、乙两只蚂蚁的行程相同,速度相同,所以甲、乙两只蚂蚁同时到达。故选C。
9、如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路(图中阴影部分),余下部分绿化,小路的宽为2cm,则两条小路的总面积是(
)。
A、108cm2
B、104cm2
C、100cm2
D、98cm2
【答案】
C
【解析】利用平移可得,两条小路的总面积是:
30×22—(30—2)×(22—2)=100cm2,故选C。
三、平移的作图
10、如图,经过平移五角星的顶点A移到了点B,作出平移后的图形。
【答案】
11、如图,直径4cm的圆O1平移5cm到圆O2,则图中阴影部分面积为__20___cm2。
【答案】∵圆O1平移5cm到圆O2,∴圆O1与圆O2全等,
∴图中的阴影部分的面积=图中的矩形的面积
∴4×5=20cm2,∴图中阴影部分面积为20cm2.
12、如图,将直角三角形ABC沿射线BC的方向平移得到三角形DEF,则图中AB=7cm,BE=4cm,GE=4cm,求图中阴影部分的面积。
【答案】∵▲ABC沿射线BC的方向平移得到▲DEF;
∴▲ABC与▲DEF全等;
∴阴影部分的面积=梯形ABEG的面积;
∴阴影部分面积=×(7+4)×4=22cm2.
13、如图,已知长方形ABCD中,AB=10cm,BC=6cm,试问将长方形ABCD沿着BC方向平移多少才能够使平移后的长方形与原来的长方形ABCD重叠部分的面积为20cm2?
【答案】解:设AE=X,根据题意列出方程:
10(6—X)=20,解得X=4
∵A的对应点为E,∴平移距离为AE的长,故向下平移4cm.
【巩固练习】
一、选择题。
1、下列现象中不属于平移的是(
)。
A、滑雪运动员在平坦的雪地上滑雪
B、彩票大转盘在旋转
C、高楼的电梯在上上下下
D、火车在一段笔直的铁轨上行驶
【答案】B
【解析】A滑雪运动员在平坦的雪地上滑雪,
属于平移,故本选项错误;B彩票大转盘在旋转,不属于平移,故本选项正确;C
高楼的电梯在上上下下,
属于平移,
故本选项错误;D
火车在一段笔直的铁轨上行驶,
属于平移,故本选项错误.故选:B.
2、如图,现将四边形ABCD沿AE进行平移,得到四边形EFGH,则图中与CG平行的线段有(
)。
A、0条
B、1条
C、2条
D、3条
3、如图所示,在一个由4×4个小正方形组成的正方形网格中,把线段EF向右平移3个单位,向下平移1个单位得到线段GH,则阴影部分面积与正方形ABCD的面积比是(
)。
A、3:4
B、5:8
C、9:16
D、1:2
【答案】B;
【解析】,,所以.
4、如图,将△ABE向右平移得到△DCF,与交于点,其中,,则(
)。
A、
B、
C、
D、
【答案】B
【解析】∵△ABE向右平移得到△DCF,∴AB∥CD,AE∥DF,∴∠DCF=∠B=45°,
∴∠CDF=180°-45°-60°=75°,∴∠AGC=∠DGE=180°-75°=105°,故选B.
5、如图,将△ABE向右平移2
cm得到△DCF,如果△ABE的周长是16
cm,那么四边形ABFD的周长是(
)。
A、16
cm
B、18
cm
C、20
cm
D、21
cm
【答案】C
【解析】已知,△ABE向右平移2
cm得到△DCF,根据平移的性质得到EF=AD=2
cm,AE=DF,又因△ABE的周长为16
cm,所以AB+BE+AE=16
cm,则四边形ABFD的周长=AB+BC+CF+DF+AD=16+2+2=20(cm),故选C.
二、填空题。
6、如图,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC'=
_________.
【答案】5
【解析】∵把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,∴三角板向右平移了5个单位,∴顶点C平移的距离CC′=5.故答案为:5.
7、如图所示,△ABC经过平移得到△A′B′C′,图中△_________与△_________大小形状不变,线段AB与A′B′的位置关系是________,线段CC′与BB′的位置关系是________.
【答案】ABC,
A′B′C′,平行,平行;
【解析】平移的性质.
8、如图,三角形ADE是由三角形DBF沿BD所在的直线平移得到的,AE,BF的延长线交于点C.若∠BFD=45°,则∠C的度数是
________。
【答案】45°;【解析】∵△ADE是由△DBF沿BD所在的直线平移得到的,
∴DE∥BC,∠BFD=∠AED,∴∠AED=∠C∴∠C=∠BFD=45°.故答案是:45°.
9、如图,
是ABC向右平移4
cm得到的,已知∠ACB=30°,B′C=3
cm,则∠C′=_________,B′C′=________cm.
【答案】30°,7
【解析】∵
是ABC向右平移4
cm得到的,∴BB′=CC′=4
cm,
∠C′=∠ACB=30°,∵B′C=3
cm,∴B′C′=4+3=7
cm.故答案为:30°,7.
10、如图所示,在长方形ABCD中,AB=10cm,BC=6cm,将长方形ABCD沿着AB方向平移________cm,才能使平移后的长方形HEFG与原来的长方形ABCD重叠部分的面积为24cm2.
【答案】6;
【解析】重叠部分长方形的一边长为6cm,另一边长为:24÷6=4
cm,
所以平移的距离为:AE=10-4=6
cm.
三、解答题。
11、如图,△ABC沿直线BC向右移了3
cm,得△FDE,且BC=6
cm,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
12、如图,将△ABC平移,可以得到△DEF,点B的对应点为点E,请画出点A的对应点D、点C的对应点F的位置,并作出△DEF.
【解析】如图:
13、如图,平面直角坐标系中,已知点A(﹣3,3),B(﹣5,1),C(﹣2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b﹣2).
(1)直接写出点C1的坐标;(2)求△AOA1的面积.
【答案】(1)、(4,﹣2);(2)、6.
【解析】(1)、根据点P的对应点坐标得出平移的法则,从而得出点C1的坐标;
(2)、利用矩形的面积减去三个直角三角形的面积得出答案.
【解答】(1)、∵点P(a,b)的对应点为P1(a+6,b﹣2),
∴平移规律为向右6个单位,向下2个单位,
∴C(﹣2,0)的对应点C1的坐标为(4,﹣2);
(2)、△AOA1的面积:6×3﹣×3×3﹣×3×1﹣×6×2=6.
14、如图是一块长方形的草地,
长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?
【解析】如图,过小路出口的一个端点作垂线,将垂线左边的图形
平移至小路右边,可得该图形的一个宽为1m,长为15m的小长方形。
故长草部分的面积为:(21—1)×15=300(m2)
15、如图,某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯,已知这种红色地毯的售价为每平方米32元,主楼梯宽为2
m,其侧面与正面如图所示,则购买地毯至少需要多少元?
【解析】利用平移线段,把楼梯的横竖向上向左平移,
构成一个长方形,长、宽分别为5米,3米,∴地毯的长度为5+3=8(米),
∴地毯的面积为8×2=16(平方米),
∴买地毯至少需要16×32=512(元).
