7.5多边形的内角和与外角和(2)-2020-2021学年苏科版七年级数学下册课件(共16张ppt)
文档属性
| 名称 | 7.5多边形的内角和与外角和(2)-2020-2021学年苏科版七年级数学下册课件(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 229.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
7.5 多边形的内角和与外角和(2)
教学目标:
掌握多边形内角和的计算方法,
能用内角和知识解决有关多边形的计算问题
【导学指导】:
一、自主学习
问题:三角形的内角和等于多少度?长方形的内角和等于多少度?正方形的内角和等于多少度?任意一个四边形的内角和等于多少度?
自主探究
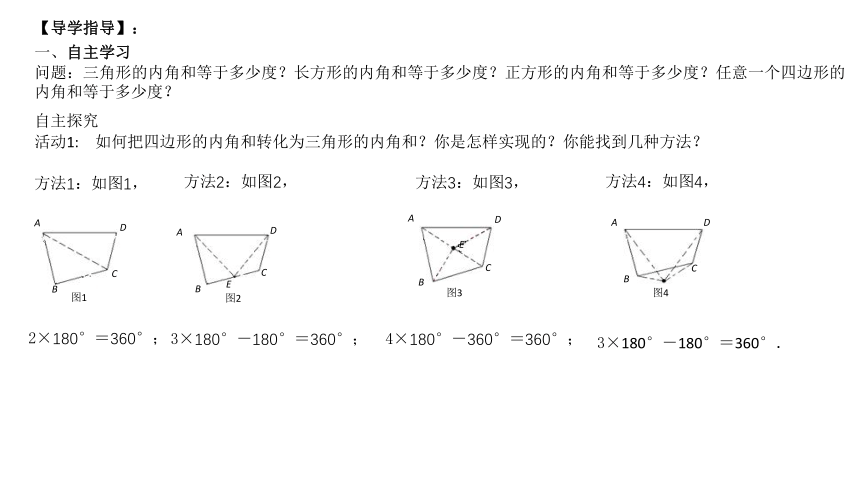
活动1: 如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?你能找到几种方法?
方法1:如图1,
A
B
C
D
图1
方法2:如图2,
A
B
D
C
E
图2
方法3:如图3,
A
B
C
D
E
图3
方法4:如图4,
2×180°=360°;
3×180°-180°=360°;
4×180°-360°=360°;
3×180°-180°=360°.
A
图4
B
C
D
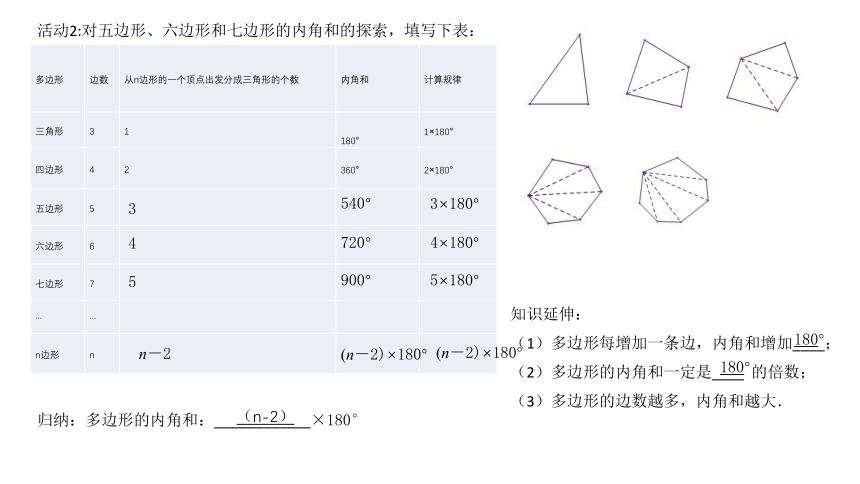
活动2:对五边形、六边形和七边形的内角和的探索,填写下表:
多边形
边数
从n边形的一个顶点出发分成三角形的个数
内角和
计算规律
三角形
3
1
180°
1×180°
四边形
4
2
360°
2×180°
五边形
5
?
?
?
六边形
6
?
?
?
七边形
7
?
?
?
…
…
?
?
?
n边形
n
?
?
?
归纳:多边形的内角和:____________×180°
知识延伸:
(1)多边形每增加一条边,内角和增加____;
(2)多边形的内角和一定是____
的倍数;
(3)多边形的边数越多,内角和越大.
3
540°
3×180°
4
720°
4×180°
5
900°
5×180°
n-2
(n-2)×180°
(n-2)×180°
180°
180°
(n-2)
活动3
(1)正多边形的特点:所有边都____,所有角都____.
(2)正多边形的内角和:____________.
(3)正多边形每个内角的度数:____________.
归纳:多边形的内角和:____________×180°
(n-2)
相等
相等
(n-2)×180°
(n-2)·180°÷n
二、例题评析:
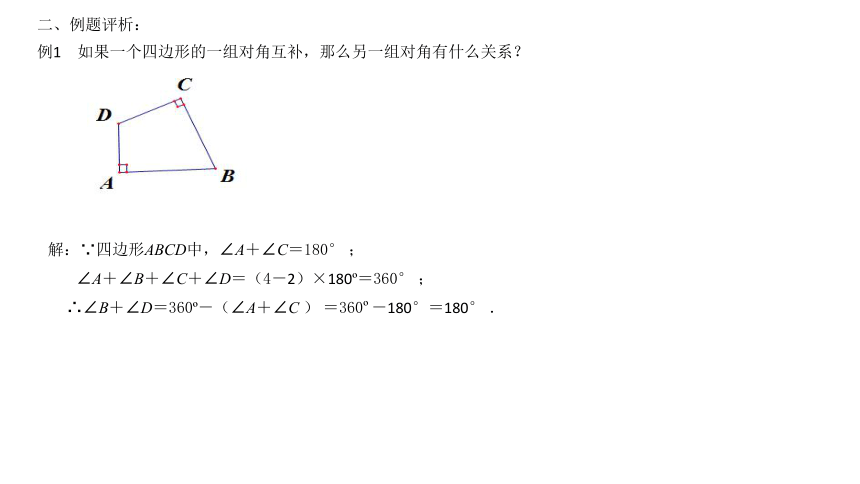
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:∵四边形ABCD中,∠A+∠C=180°
;
∠A+∠B+∠C+∠D=(4-2)×180?=360°
;
∴∠B+∠D=360?-(∠A+∠C
)
=360?-180°=180°
.
例2.
在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,求∠A、∠B、∠C的度数.
解:设∠A=x°,则∠B=x°+20°,∠C=2x°.
由四边形的内角和定理,得x°+(x°+20°)+2x°+60°=360°,
解得x=70.
所以∠A=70°,∠B=90°,∠C=140°
三、巩固知识
[典型问题]
练习1
(1)八边形内角和是____°;(2)十六边形内角和是______°;
(3)如果一个多边形的边数增加1,那么这时它的内角和增加了____度
练习2
一个多边形的内角和等于1440°,它是几边形?
练习3 求图中x的值.
140°
1080
2520
180
解:设这个多边形是n边形,依题意得,180?×(n-2)=
1440°
解得:n=10.
答:这个多边形是十边形.
解:140?+90?+x+x=180?×(4-2)
x=65°.
[四基训练]
1.内角和为540°的多边形是(
)
A.三角形
B.四边形
C.五边形
D.六边形
2.若一个多边形的每个内角都为108°,则它的边数为(
)
A.5
B.8
C.6
D.10
解:由多边形的内角和公式可得
(n-2)×180°=540°,
解得:n=5,
故选:C.
解:已知多边形的每一个内角都等于108°,可得多边形的每一个外角都等于180°-108°=72°,所以多边形的边数n=360°÷72°=5.故选A.
3.如图,已知△ABC中,∠A=75°,则∠1+∠2=(
)
A.335°°
B.255°
C.155°
D.150°
解:∵∠A+∠B+∠C=180°,∠A=75°,
∴∠B+∠C=180°﹣∠A=105°.
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣105°=255°.
故选B.
4.如图,在五边形ABCDE中,∠A
+∠B+
∠E=α,DP、CP分别平分∠EDC、
∠BCD,则∠P的度教是(
)
5.将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2等于( )
A.10°
B.15°
C.20°
D.35°
解:如图,∵∠C=50°,
∴∠3+∠4=∠A+∠B=∠A′+∠B′=180°﹣∠C=130°,
∵∠1+∠2+∠3+∠4+∠A′+∠B′=360°,∠1=85°,
∴∠2=360°﹣85°﹣2×130°=15°,
故选:B.
6.如图,将四边形纸片ABCD沿MN折叠,若∠1+∠2=130°,则∠B+∠C=( )
A.115°
B.130°
C.135°
D.150°
7.一个n边形的内角和为1080°,则n=________.
8.如图,从ΔABC纸片中剪去ΔCDE,得到四边形ABCD.如果∠1+∠2=230°,那么∠C_______.
解:(n﹣2)?180°=1080°,解得n=8.
解:如图
因为四边形ABCD的内角和为360°,且∠1+∠2=230°.
所以∠A+∠B=360°-230°=130°.
因为△ABD的内角和为180°,
所以∠C=180°-(∠A+∠B)
=180°-130°=50°.
9.如图,AC是正五边形ABCDE的一条对角线,则∠ACB=_____.
10.
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是________°.
解:∵五边形ABCDE是正五边形,
∴∠B=108°,AB=CB,
∴∠ACB=(180°﹣108°)÷2=36°;
故答案为36°.
解:连接BE,则∠C+∠D=∠CBE+∠DEB,
所以∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G的度数等于五边形
ABEFG的内角和540°.
11.如图,五边形ABCDE的各个内角都相等,且AB∥EC,那么∠DEC与∠DCE相等吗?为什么?
解:∠DEC=∠DCE
因为五边形的内角和是(5-2)×180°=540°,且每个内角都相等,
所以每个内角的度数为540°÷5=108°,
即∠A=∠AED=∠D=108°.
因为AB∥EC,
所以∠A+∠AEC=180°.
所以∠AEC=180°-∠A=72°.
所以∠DEC=∠AED-∠AEC=36°.
因为△DEC的内角和为180°,
所以∠DCE=180°-∠DEC-∠D=36°.
所以∠DEC=∠DCE
[拓展提升]
?
12.从如图的五边形ABCDE纸片中减去一个三角形,剩余部分的多边形的内角和和是________
【分析】从一个五边形中剪去一个三角形,得到的可能是四边形、可能是五边形、可能是六边形,再根据多边形的内角和的公式求解.
7.5 多边形的内角和与外角和(2)
教学目标:
掌握多边形内角和的计算方法,
能用内角和知识解决有关多边形的计算问题
【导学指导】:
一、自主学习
问题:三角形的内角和等于多少度?长方形的内角和等于多少度?正方形的内角和等于多少度?任意一个四边形的内角和等于多少度?
自主探究
活动1: 如何把四边形的内角和转化为三角形的内角和?你是怎样实现的?你能找到几种方法?
方法1:如图1,
A
B
C
D
图1
方法2:如图2,
A
B
D
C
E
图2
方法3:如图3,
A
B
C
D
E
图3
方法4:如图4,
2×180°=360°;
3×180°-180°=360°;
4×180°-360°=360°;
3×180°-180°=360°.
A
图4
B
C
D
活动2:对五边形、六边形和七边形的内角和的探索,填写下表:
多边形
边数
从n边形的一个顶点出发分成三角形的个数
内角和
计算规律
三角形
3
1
180°
1×180°
四边形
4
2
360°
2×180°
五边形
5
?
?
?
六边形
6
?
?
?
七边形
7
?
?
?
…
…
?
?
?
n边形
n
?
?
?
归纳:多边形的内角和:____________×180°
知识延伸:
(1)多边形每增加一条边,内角和增加____;
(2)多边形的内角和一定是____
的倍数;
(3)多边形的边数越多,内角和越大.
3
540°
3×180°
4
720°
4×180°
5
900°
5×180°
n-2
(n-2)×180°
(n-2)×180°
180°
180°
(n-2)
活动3
(1)正多边形的特点:所有边都____,所有角都____.
(2)正多边形的内角和:____________.
(3)正多边形每个内角的度数:____________.
归纳:多边形的内角和:____________×180°
(n-2)
相等
相等
(n-2)×180°
(n-2)·180°÷n
二、例题评析:
例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
解:∵四边形ABCD中,∠A+∠C=180°
;
∠A+∠B+∠C+∠D=(4-2)×180?=360°
;
∴∠B+∠D=360?-(∠A+∠C
)
=360?-180°=180°
.
例2.
在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,求∠A、∠B、∠C的度数.
解:设∠A=x°,则∠B=x°+20°,∠C=2x°.
由四边形的内角和定理,得x°+(x°+20°)+2x°+60°=360°,
解得x=70.
所以∠A=70°,∠B=90°,∠C=140°
三、巩固知识
[典型问题]
练习1
(1)八边形内角和是____°;(2)十六边形内角和是______°;
(3)如果一个多边形的边数增加1,那么这时它的内角和增加了____度
练习2
一个多边形的内角和等于1440°,它是几边形?
练习3 求图中x的值.
140°
1080
2520
180
解:设这个多边形是n边形,依题意得,180?×(n-2)=
1440°
解得:n=10.
答:这个多边形是十边形.
解:140?+90?+x+x=180?×(4-2)
x=65°.
[四基训练]
1.内角和为540°的多边形是(
)
A.三角形
B.四边形
C.五边形
D.六边形
2.若一个多边形的每个内角都为108°,则它的边数为(
)
A.5
B.8
C.6
D.10
解:由多边形的内角和公式可得
(n-2)×180°=540°,
解得:n=5,
故选:C.
解:已知多边形的每一个内角都等于108°,可得多边形的每一个外角都等于180°-108°=72°,所以多边形的边数n=360°÷72°=5.故选A.
3.如图,已知△ABC中,∠A=75°,则∠1+∠2=(
)
A.335°°
B.255°
C.155°
D.150°
解:∵∠A+∠B+∠C=180°,∠A=75°,
∴∠B+∠C=180°﹣∠A=105°.
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=360°﹣105°=255°.
故选B.
4.如图,在五边形ABCDE中,∠A
+∠B+
∠E=α,DP、CP分别平分∠EDC、
∠BCD,则∠P的度教是(
)
5.将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2等于( )
A.10°
B.15°
C.20°
D.35°
解:如图,∵∠C=50°,
∴∠3+∠4=∠A+∠B=∠A′+∠B′=180°﹣∠C=130°,
∵∠1+∠2+∠3+∠4+∠A′+∠B′=360°,∠1=85°,
∴∠2=360°﹣85°﹣2×130°=15°,
故选:B.
6.如图,将四边形纸片ABCD沿MN折叠,若∠1+∠2=130°,则∠B+∠C=( )
A.115°
B.130°
C.135°
D.150°
7.一个n边形的内角和为1080°,则n=________.
8.如图,从ΔABC纸片中剪去ΔCDE,得到四边形ABCD.如果∠1+∠2=230°,那么∠C_______.
解:(n﹣2)?180°=1080°,解得n=8.
解:如图
因为四边形ABCD的内角和为360°,且∠1+∠2=230°.
所以∠A+∠B=360°-230°=130°.
因为△ABD的内角和为180°,
所以∠C=180°-(∠A+∠B)
=180°-130°=50°.
9.如图,AC是正五边形ABCDE的一条对角线,则∠ACB=_____.
10.
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数是________°.
解:∵五边形ABCDE是正五边形,
∴∠B=108°,AB=CB,
∴∠ACB=(180°﹣108°)÷2=36°;
故答案为36°.
解:连接BE,则∠C+∠D=∠CBE+∠DEB,
所以∠A+∠ABC+∠C+∠D+∠DEF+∠F+∠G的度数等于五边形
ABEFG的内角和540°.
11.如图,五边形ABCDE的各个内角都相等,且AB∥EC,那么∠DEC与∠DCE相等吗?为什么?
解:∠DEC=∠DCE
因为五边形的内角和是(5-2)×180°=540°,且每个内角都相等,
所以每个内角的度数为540°÷5=108°,
即∠A=∠AED=∠D=108°.
因为AB∥EC,
所以∠A+∠AEC=180°.
所以∠AEC=180°-∠A=72°.
所以∠DEC=∠AED-∠AEC=36°.
因为△DEC的内角和为180°,
所以∠DCE=180°-∠DEC-∠D=36°.
所以∠DEC=∠DCE
[拓展提升]
?
12.从如图的五边形ABCDE纸片中减去一个三角形,剩余部分的多边形的内角和和是________
【分析】从一个五边形中剪去一个三角形,得到的可能是四边形、可能是五边形、可能是六边形,再根据多边形的内角和的公式求解.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
