2020-2021学年苏科版八年级数学下册11.3用反比例函数解决问题(2)培优训练(word解析版)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学下册11.3用反比例函数解决问题(2)培优训练(word解析版) | 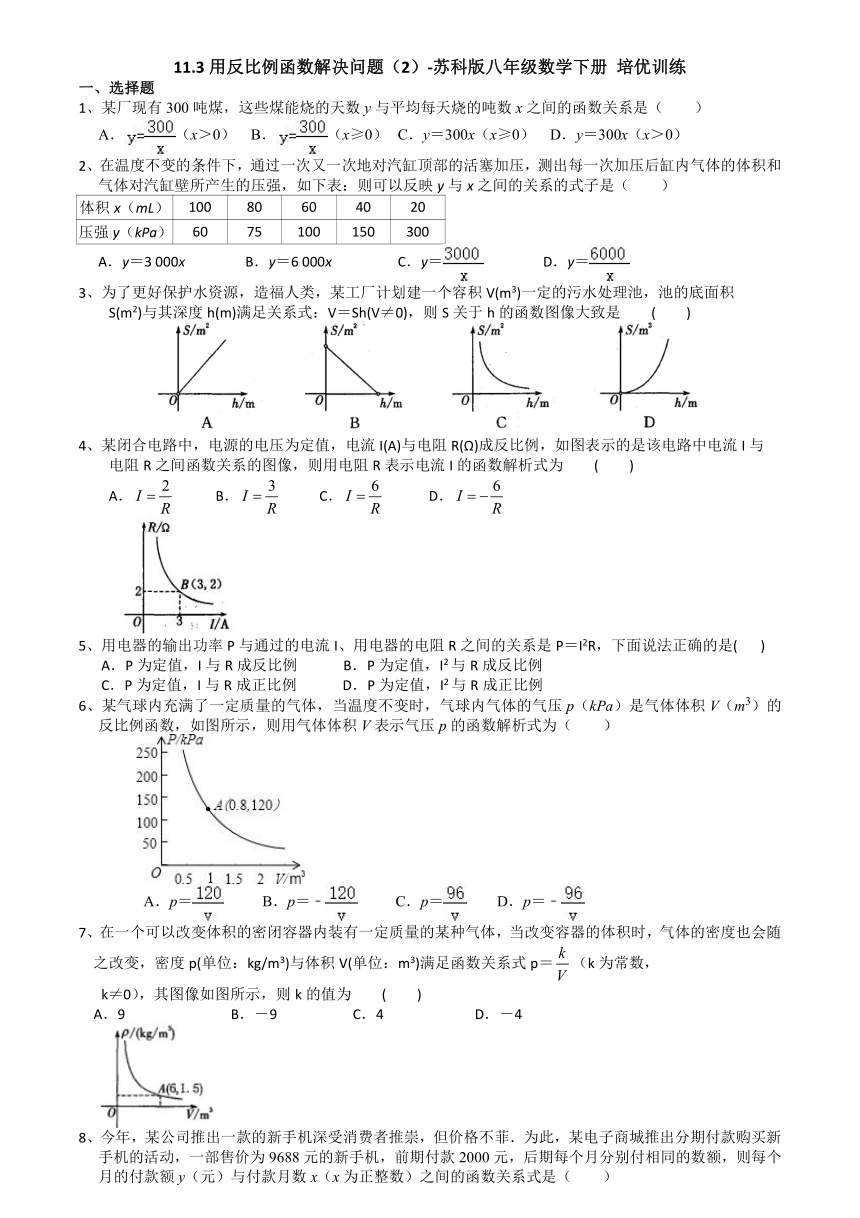 | |
| 格式 | zip | ||
| 文件大小 | 409.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-21 07:00:49 | ||
图片预览



文档简介
11.3用反比例函数解决问题(2)-苏科版八年级数学下册
培优训练
一、选择题
1、某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0)
B.(x≥0)
C.y=300x(x≥0)
D.y=300x(x>0)
2、在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积x(mL)
100
80
60
40
20
压强y(kPa)
60
75
100
150
300
A.y=3
000x
B.y=6
000x
C.y=
D.y=
3、为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积
S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图像大致是
(
)
4、某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示的是该电路中电流I与
电阻R之间函数关系的图像,则用电阻R表示电流I的函数解析式为
(
)
A.
B.
C.
D.
5、用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,下面说法正确的是(
)
A.P为定值,I与R成反比例
B.P为定值,I2与R成反比例
C.P为定值,I与R成正比例
D.P为定值,I2与R成正比例
6、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,如图所示,则用气体体积V表示气压p的函数解析式为( )
A.p=
B.p=﹣
C.p=
D.p=﹣
7、在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度p(单位:kg/m3)与体积V(单位:m3)满足函数关系式p=(k为常数,
k≠0),其图像如图所示,则k的值为
(
)
A.9
B.-9
C.4
D.-4
8、今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A.y=+2000
B.y=﹣2000
C.y=
D.y=
9、已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
二、填空题
10、在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,
p=50,则当p=25时,V=_
_____.
11、某商场出售一批进价为2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元)
…
3
4
5
6
…
日销售量y(个)
…
20
15
12
10
…
则y与x之间的函数关系式为
.
12、某种汽车可装油400L,若汽车每小时的用油量为(L).
(1)用油量与每小时的用油量(L)的函数关系式为
;
(2)若每小时的用油量为20L,则这些油可用的时间为
;
(3)若要使汽车继续行驶40不需供油,则每小时用油量的范围是
.
13、如图,一块长方体大理石板的A、B、C三个面上的边长如图所示,如果大理石板的A面向下放在地上
时地面所受压强为m帕,则把大理石板B面向下放在地上,地面所受压强是______m帕.
14、已知,在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函
数关系,其图像如图所示,则当力达到20牛时,此物体在力的方向上移动的距离是______米.
15、学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场.
设它的一边长为x(米),则另一边的长y(米)与x的函数关系式为
.
16、某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年
度
2008
2009
2010
2011
投入技术改进资金x(万元)
2.5
3
4
4.5
产品成本y(万元∕件)
7.2
6
4.5
4
17、一定质量的二氧化碳,其体积V(是密度的反比例函数,请你根据图中的已知条件,下出反比例函数的关系式
,当V=1.9时,=
.
18、近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式为
.(无需确定x的取值范围)
三、解答题
19、蓄电池的电压为定值,使用此电源时,电流I(
A
)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当R=10Ω时,电流能是4A吗?为什么?
20、为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒.
已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=(a为常数),如图所示.
根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
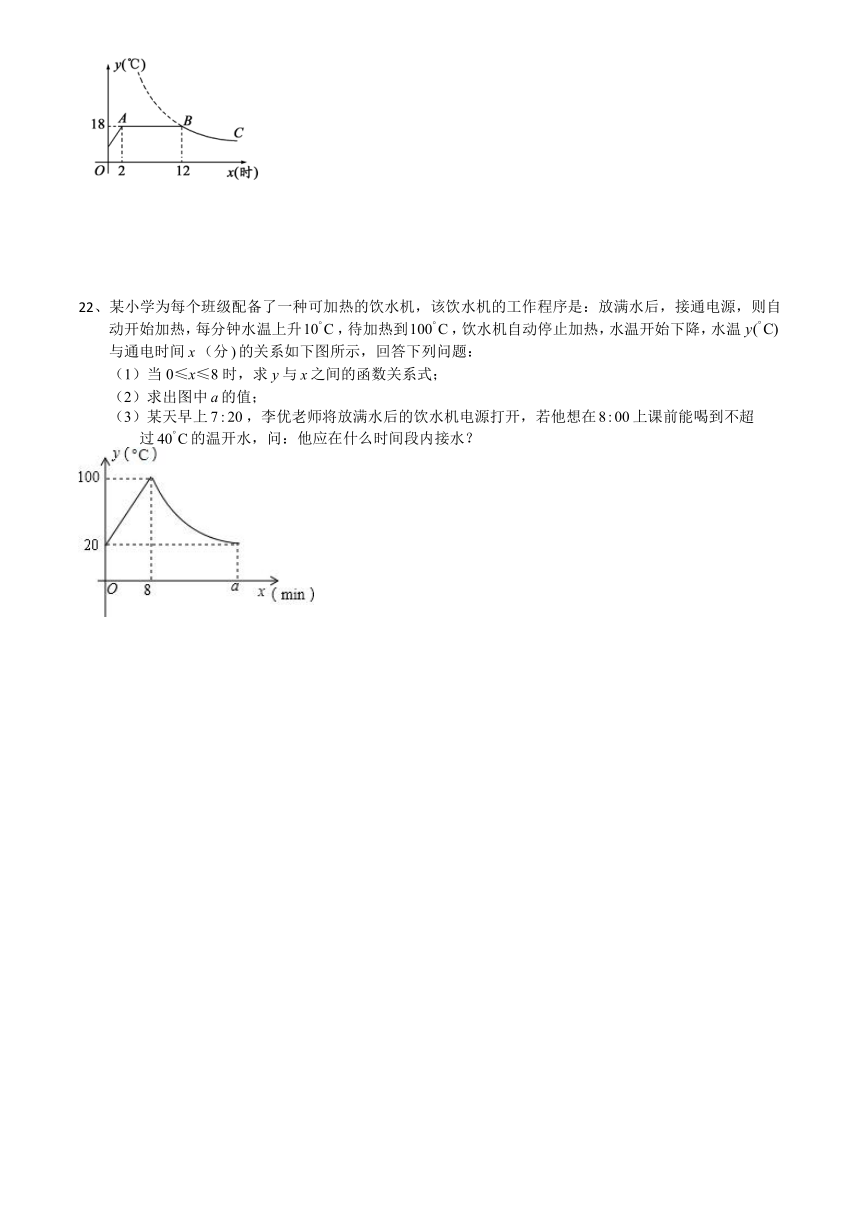
21、我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
22、某小学为每个班级配备了一种可加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升,待加热到,饮水机自动停止加热,水温开始下降,水温与通电时间(分的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求与之间的函数关系式;
(2)求出图中的值;
(3)某天早上,李优老师将放满水后的饮水机电源打开,若他想在上课前能喝到不超
过的温开水,问:他应在什么时间段内接水?
11.3用反比例函数解决问题(2)-苏科版八年级数学下册
培优训练(答案)
一、选择题
1、某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0)
B.(x≥0)
C.y=300x(x≥0)
D.y=300x(x>0)
【解答】解:∵煤的总吨数为300,平均每天烧煤的吨数为x,
∴这些煤能烧的天数为y=(x>0),
故选:A.
2、在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积x(mL)
100
80
60
40
20
压强y(kPa)
60
75
100
150
300
A.y=3
000x
B.y=6
000x
C.y=
D.y=
【解答】解:由表格数据可得:此函数是反比例函数,设解析式为:y=,
则xy=k=6000,
故y与x之间的关系的式子是y=,
故选:D.
3、为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积
S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图像大致是
(
C
)
4、某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示的是该电路中电流I与
电阻R之间函数关系的图像,则用电阻R表示电流I的函数解析式为
(
C
)
A.
B.
C.
D.
5、用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,下面说法正确的是(
B
)
A.P为定值,I与R成反比例
B.P为定值,I2与R成反比例
C.P为定值,I与R成正比例
D.P为定值,I2与R成正比例
6、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,如图所示,则用气体体积V表示气压p的函数解析式为( )
A.p=
B.p=﹣
C.p=
D.p=﹣
【解答】解:设P=,那么点(0.8,120)在此函数解析式上,则k=0.8×120=96,
∴p=.故选:C.
7、在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度p(单位:kg/m3)与体积V(单位:m3)满足函数关系式p=(k为常数,
k≠0),其图像如图所示,则k的值为
(
A
)
A.9
B.-9
C.4
D.-4
8、今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A.y=+2000
B.y=﹣2000
C.y=
D.y=
【解答】解:由题意可得:y==.
故选:C.
9、已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
【解答】解:设用电阻R表示电流I的函数解析式为I=,
∵过(2,3),∴k=3×2=6,∴I=,
故选:D.
二、填空题
10、在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,
p=50,则当p=25时,V=__400
_____.
11、某商场出售一批进价为2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元)
…
3
4
5
6
…
日销售量y(个)
…
20
15
12
10
…
则y与x之间的函数关系式为
.
【解答】解:因为x与y的乘积是相同的,所以可知y与x成反比例,
设y=,
将(3,20)代入可得:20=,解得:k=60.
则y与x之间的函数关系式为y=.
故答案为:y=.
12、某种汽车可装油400L,若汽车每小时的用油量为(L).
(1)用油量与每小时的用油量(L)的函数关系式为
;
(2)若每小时的用油量为20L,则这些油可用的时间为
;
(3)若要使汽车继续行驶40不需供油,则每小时用油量的范围是
.
答案:(1);(2);(3)。
13、如图,一块长方体大理石板的A、B、C三个面上的边长如图所示,如果大理石板的A面向下放在地上
时地面所受压强为m帕,则把大理石板B面向下放在地上,地面所受压强是__3_____m帕.
14、已知,在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函
数关系,其图像如图所示,则当力达到20牛时,此物体在力的方向上移动的距离是_36_____米.
15、学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场.
设它的一边长为x(米),则另一边的长y(米)与x的函数关系式为
.
16、某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年
度
2008
2009
2010
2011
投入技术改进资金x(万元)
2.5
3
4
4.5
产品成本y(万元∕件)
7.2
6
4.5
4
【解答】解:有题意可得此函数解析式为反比例函数解析式,设其为解析式为y=.
当x=2.5时,y=7.2,可得:7.2=,解得k=18
∴反比例函数是y=.故答案为:y=.
17、一定质量的二氧化碳,其体积V(是密度的反比例函数,请你根据图中的已知条件,下出反比例函数的关系式
,当V=1.9时,=
.
答案:,
18、近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式为
.(无需确定x的取值范围)
【解答】解:根据题意近视眼镜的度数y(度)与镜片焦距x(米)成反比例,设y=,
由于点(0.25,400)在此函数解析式上,
∴k=0.25×400=100,∴y=.
故答案为:y=.
三、解答题
19、蓄电池的电压为定值,使用此电源时,电流I(
A
)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当R=10Ω时,电流能是4A吗?为什么?
解:(1)∵电流I(
A
)是电阻R(Ω)的反比例函数,∴设I=(k≠0),
把(4,9)代入得:k=4×9=36,∴I=;
(2)当R=10Ω时,I=3.6≠4,∴电流不可能是4A.
20、为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒.
已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=(a为常数),如图所示.
根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
【详解】(1)
将点代入函数关系式,
解得,
有
将代入,
得,
所以所求反比例函数关系式为;
再将代入,
得,所以所求正比例函数关系式为.
(2)
解不等式,
解得,
所以至少需要经过6小时后,学生才能进入教室.
21、我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
解:(1)恒温系统在这天保持大棚温度为18℃的时间为10小时
(2)∵点B(12,18)在双曲线y=上,∴18=,∴解得k=216
(3)当x=16时,y==13.5,所以当x=16时,大棚内的温度约为13.5℃.
22、某小学为每个班级配备了一种可加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升,待加热到,饮水机自动停止加热,水温开始下降,水温与通电时间(分的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求与之间的函数关系式;
(2)求出图中的值;
(3)某天早上,李优老师将放满水后的饮水机电源打开,若他想在上课前能喝到不超
过的温开水,问:他应在什么时间段内接水?
【答案】解:(1)当0≤x≤8时,设y与x之间的函数关系式为y=kx+b(k≠0),
将(0,20),(8,100)代入y=kx+b,得:,解得:,
∴当0≤x≤8时,y与x之间的函数关系式为y=10x+20;
(2)当8≤x≤a时,设y与x之间的函数关系式为:y=(k2≠0),
将(8,100)代入y=,得:100=
解得:k2=800,
∴当8≤x≤a时,y与x之间的函数关系式为:y=;
将(a,20)代入y=,得:a=40;
(3)依题意,得:≤40,解得:x≥20.
∵x≤40,∴20≤x≤40.
∴他应在7:40~8:00时间段内接水.
培优训练
一、选择题
1、某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0)
B.(x≥0)
C.y=300x(x≥0)
D.y=300x(x>0)
2、在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积x(mL)
100
80
60
40
20
压强y(kPa)
60
75
100
150
300
A.y=3
000x
B.y=6
000x
C.y=
D.y=
3、为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积
S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图像大致是
(
)
4、某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示的是该电路中电流I与
电阻R之间函数关系的图像,则用电阻R表示电流I的函数解析式为
(
)
A.
B.
C.
D.
5、用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,下面说法正确的是(
)
A.P为定值,I与R成反比例
B.P为定值,I2与R成反比例
C.P为定值,I与R成正比例
D.P为定值,I2与R成正比例
6、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,如图所示,则用气体体积V表示气压p的函数解析式为( )
A.p=
B.p=﹣
C.p=
D.p=﹣
7、在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度p(单位:kg/m3)与体积V(单位:m3)满足函数关系式p=(k为常数,
k≠0),其图像如图所示,则k的值为
(
)
A.9
B.-9
C.4
D.-4
8、今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A.y=+2000
B.y=﹣2000
C.y=
D.y=
9、已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
二、填空题
10、在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,
p=50,则当p=25时,V=_
_____.
11、某商场出售一批进价为2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元)
…
3
4
5
6
…
日销售量y(个)
…
20
15
12
10
…
则y与x之间的函数关系式为
.
12、某种汽车可装油400L,若汽车每小时的用油量为(L).
(1)用油量与每小时的用油量(L)的函数关系式为
;
(2)若每小时的用油量为20L,则这些油可用的时间为
;
(3)若要使汽车继续行驶40不需供油,则每小时用油量的范围是
.
13、如图,一块长方体大理石板的A、B、C三个面上的边长如图所示,如果大理石板的A面向下放在地上
时地面所受压强为m帕,则把大理石板B面向下放在地上,地面所受压强是______m帕.
14、已知,在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函
数关系,其图像如图所示,则当力达到20牛时,此物体在力的方向上移动的距离是______米.
15、学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场.
设它的一边长为x(米),则另一边的长y(米)与x的函数关系式为
.
16、某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年
度
2008
2009
2010
2011
投入技术改进资金x(万元)
2.5
3
4
4.5
产品成本y(万元∕件)
7.2
6
4.5
4
17、一定质量的二氧化碳,其体积V(是密度的反比例函数,请你根据图中的已知条件,下出反比例函数的关系式
,当V=1.9时,=
.
18、近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式为
.(无需确定x的取值范围)
三、解答题
19、蓄电池的电压为定值,使用此电源时,电流I(
A
)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当R=10Ω时,电流能是4A吗?为什么?
20、为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒.
已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=(a为常数),如图所示.
根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
21、我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
22、某小学为每个班级配备了一种可加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升,待加热到,饮水机自动停止加热,水温开始下降,水温与通电时间(分的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求与之间的函数关系式;
(2)求出图中的值;
(3)某天早上,李优老师将放满水后的饮水机电源打开,若他想在上课前能喝到不超
过的温开水,问:他应在什么时间段内接水?
11.3用反比例函数解决问题(2)-苏科版八年级数学下册
培优训练(答案)
一、选择题
1、某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0)
B.(x≥0)
C.y=300x(x≥0)
D.y=300x(x>0)
【解答】解:∵煤的总吨数为300,平均每天烧煤的吨数为x,
∴这些煤能烧的天数为y=(x>0),
故选:A.
2、在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,如下表:则可以反映y与x之间的关系的式子是( )
体积x(mL)
100
80
60
40
20
压强y(kPa)
60
75
100
150
300
A.y=3
000x
B.y=6
000x
C.y=
D.y=
【解答】解:由表格数据可得:此函数是反比例函数,设解析式为:y=,
则xy=k=6000,
故y与x之间的关系的式子是y=,
故选:D.
3、为了更好保护水资源,造福人类,某工厂计划建一个容积V(m3)一定的污水处理池,池的底面积
S(m2)与其深度h(m)满足关系式:V=Sh(V≠0),则S关于h的函数图像大致是
(
C
)
4、某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示的是该电路中电流I与
电阻R之间函数关系的图像,则用电阻R表示电流I的函数解析式为
(
C
)
A.
B.
C.
D.
5、用电器的输出功率P与通过的电流I、用电器的电阻R之间的关系是P=I2R,下面说法正确的是(
B
)
A.P为定值,I与R成反比例
B.P为定值,I2与R成反比例
C.P为定值,I与R成正比例
D.P为定值,I2与R成正比例
6、某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,如图所示,则用气体体积V表示气压p的函数解析式为( )
A.p=
B.p=﹣
C.p=
D.p=﹣
【解答】解:设P=,那么点(0.8,120)在此函数解析式上,则k=0.8×120=96,
∴p=.故选:C.
7、在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度p(单位:kg/m3)与体积V(单位:m3)满足函数关系式p=(k为常数,
k≠0),其图像如图所示,则k的值为
(
A
)
A.9
B.-9
C.4
D.-4
8、今年,某公司推出一款的新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9688元的新手机,前期付款2000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是( )
A.y=+2000
B.y=﹣2000
C.y=
D.y=
【解答】解:由题意可得:y==.
故选:C.
9、已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A.
B.
C.
D.
【解答】解:设用电阻R表示电流I的函数解析式为I=,
∵过(2,3),∴k=3×2=6,∴I=,
故选:D.
二、填空题
10、在温度不变的条件下,一定质量的气体的压强p与它的体积V成反比例,当V=200时,
p=50,则当p=25时,V=__400
_____.
11、某商场出售一批进价为2元的贺卡,在市场营销中发现此贺卡的日销售单价x(元)与日销售量y(个)之间有如下关系:
日销售单价x(元)
…
3
4
5
6
…
日销售量y(个)
…
20
15
12
10
…
则y与x之间的函数关系式为
.
【解答】解:因为x与y的乘积是相同的,所以可知y与x成反比例,
设y=,
将(3,20)代入可得:20=,解得:k=60.
则y与x之间的函数关系式为y=.
故答案为:y=.
12、某种汽车可装油400L,若汽车每小时的用油量为(L).
(1)用油量与每小时的用油量(L)的函数关系式为
;
(2)若每小时的用油量为20L,则这些油可用的时间为
;
(3)若要使汽车继续行驶40不需供油,则每小时用油量的范围是
.
答案:(1);(2);(3)。
13、如图,一块长方体大理石板的A、B、C三个面上的边长如图所示,如果大理石板的A面向下放在地上
时地面所受压强为m帕,则把大理石板B面向下放在地上,地面所受压强是__3_____m帕.
14、已知,在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函
数关系,其图像如图所示,则当力达到20牛时,此物体在力的方向上移动的距离是_36_____米.
15、学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场.
设它的一边长为x(米),则另一边的长y(米)与x的函数关系式为
.
16、某高科技开发公司从2008年起开始投入技术改进资金,经过技术改进后,其产品的生产成本不断降低,具体数据如下表:请你认真分析表中数据,写出可以表示该变化规律的表达式是
年
度
2008
2009
2010
2011
投入技术改进资金x(万元)
2.5
3
4
4.5
产品成本y(万元∕件)
7.2
6
4.5
4
【解答】解:有题意可得此函数解析式为反比例函数解析式,设其为解析式为y=.
当x=2.5时,y=7.2,可得:7.2=,解得k=18
∴反比例函数是y=.故答案为:y=.
17、一定质量的二氧化碳,其体积V(是密度的反比例函数,请你根据图中的已知条件,下出反比例函数的关系式
,当V=1.9时,=
.
答案:,
18、近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式为
.(无需确定x的取值范围)
【解答】解:根据题意近视眼镜的度数y(度)与镜片焦距x(米)成反比例,设y=,
由于点(0.25,400)在此函数解析式上,
∴k=0.25×400=100,∴y=.
故答案为:y=.
三、解答题
19、蓄电池的电压为定值,使用此电源时,电流I(
A
)是电阻R(Ω)的反比例函数,其图象如图所示.
(1)求这个反比例函数的表达式;
(2)当R=10Ω时,电流能是4A吗?为什么?
解:(1)∵电流I(
A
)是电阻R(Ω)的反比例函数,∴设I=(k≠0),
把(4,9)代入得:k=4×9=36,∴I=;
(2)当R=10Ω时,I=3.6≠4,∴电流不可能是4A.
20、为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒.
已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=(a为常数),如图所示.
根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?
【详解】(1)
将点代入函数关系式,
解得,
有
将代入,
得,
所以所求反比例函数关系式为;
再将代入,
得,所以所求正比例函数关系式为.
(2)
解不等式,
解得,
所以至少需要经过6小时后,学生才能进入教室.
21、我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
解:(1)恒温系统在这天保持大棚温度为18℃的时间为10小时
(2)∵点B(12,18)在双曲线y=上,∴18=,∴解得k=216
(3)当x=16时,y==13.5,所以当x=16时,大棚内的温度约为13.5℃.
22、某小学为每个班级配备了一种可加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升,待加热到,饮水机自动停止加热,水温开始下降,水温与通电时间(分的关系如下图所示,回答下列问题:
(1)当0≤x≤8时,求与之间的函数关系式;
(2)求出图中的值;
(3)某天早上,李优老师将放满水后的饮水机电源打开,若他想在上课前能喝到不超
过的温开水,问:他应在什么时间段内接水?
【答案】解:(1)当0≤x≤8时,设y与x之间的函数关系式为y=kx+b(k≠0),
将(0,20),(8,100)代入y=kx+b,得:,解得:,
∴当0≤x≤8时,y与x之间的函数关系式为y=10x+20;
(2)当8≤x≤a时,设y与x之间的函数关系式为:y=(k2≠0),
将(8,100)代入y=,得:100=
解得:k2=800,
∴当8≤x≤a时,y与x之间的函数关系式为:y=;
将(a,20)代入y=,得:a=40;
(3)依题意,得:≤40,解得:x≥20.
∵x≤40,∴20≤x≤40.
∴他应在7:40~8:00时间段内接水.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
