2020—2021学年苏科版七年级数学下册第七章 平面图形的认识(二)选择题培优(一)(word版含解析)
文档属性
| 名称 | 2020—2021学年苏科版七年级数学下册第七章 平面图形的认识(二)选择题培优(一)(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 128.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-20 15:33:20 | ||
图片预览



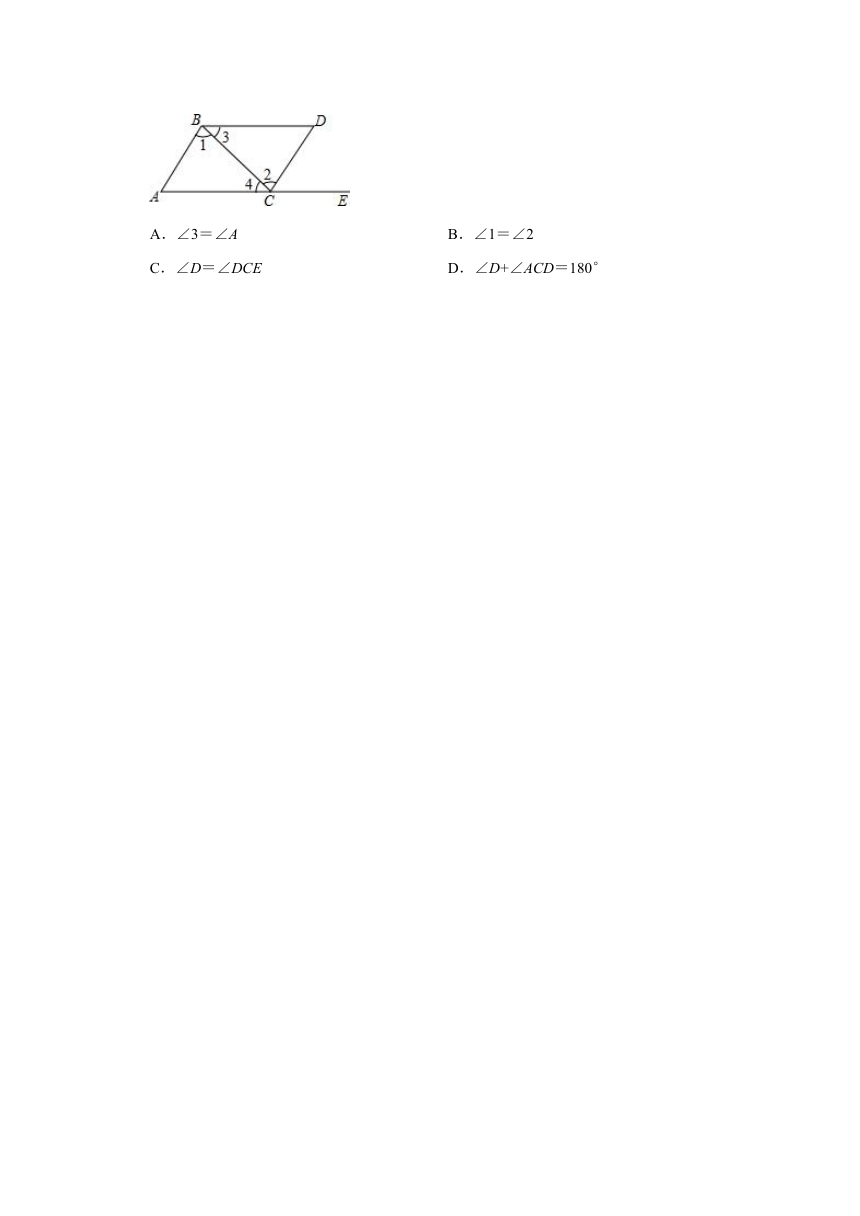
文档简介
苏科版七年级数学下册第七章
《平面图形的认识》
选择题培优(一)
1.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80°
B.85°
C.90°
D.95°
2.将一个直角三角板与两边平行的纸条按如图所示的方式放置,若∠2=40°,则∠1的大小是( )
A.40°
B.50°
C.60°
D.70°
3.如图,∠1=∠2,∠D=50°,则∠B的度数为( )
A.50°
B.40°
C.100°
D.130°
4.AF是∠BAC的平分线,DF∥AC,若∠BAC=70°,则∠1的度数为( )
A.175°
B.35°
C.55°
D.70°
5.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等
B.互余或互补
C.互补
D.相等或互补
6.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.90°
B.135°
C.270°
D.315°
7.适合条件∠A=∠B=∠C的△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
8.如果将一副三角板按如图方式叠放,那么∠1等于( )
A.120°
B.105°
C.60°
D.45°
9.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20°
B.30°
C.50°
D.70°
10.如图,在平移三角尺画平行线的过程中,理由是( )
A.两直线平行,同位角相等
B.两直线平行,内错角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行
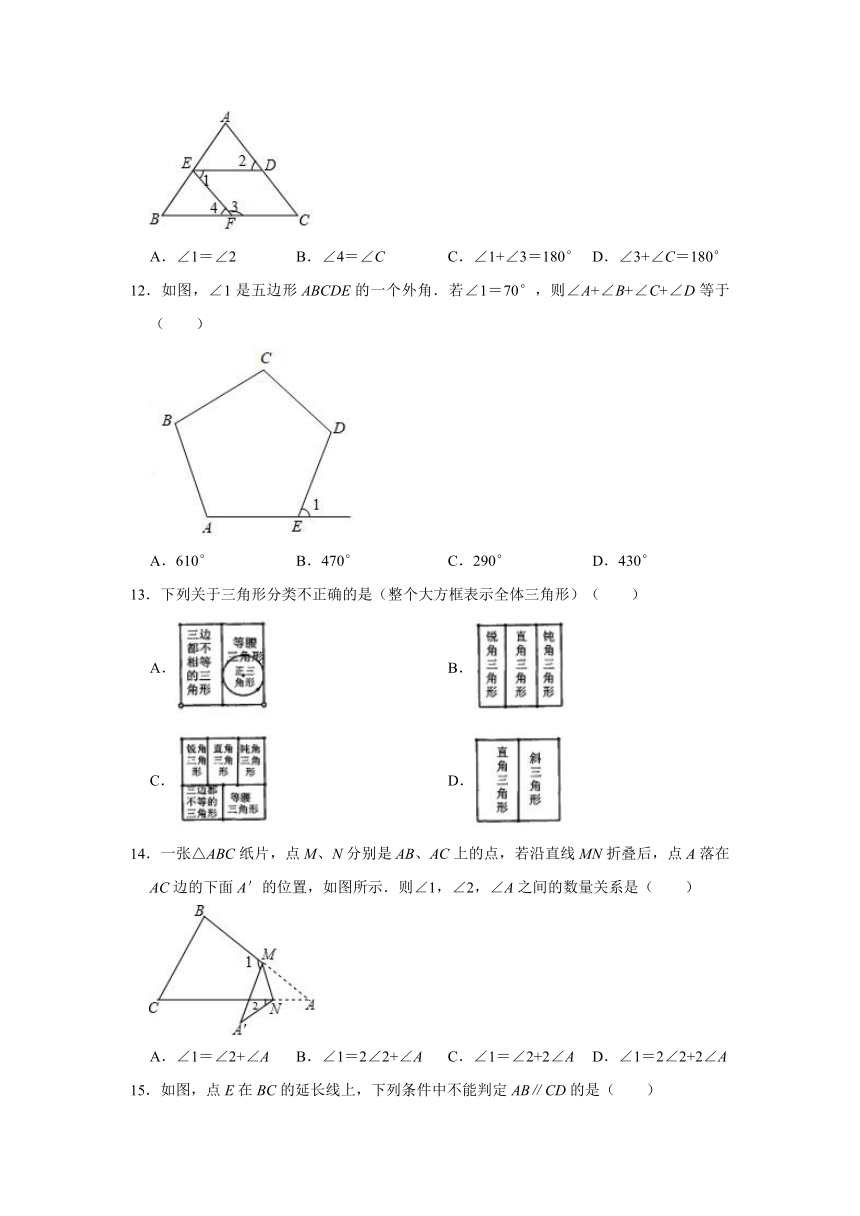
11.如图,下面哪个条件能判断DE∥BC的是( )
A.∠1=∠2
B.∠4=∠C
C.∠1+∠3=180°
D.∠3+∠C=180°
12.如图,∠1是五边形ABCDE的一个外角.若∠1=70°,则∠A+∠B+∠C+∠D等于( )
A.610°
B.470°
C.290°
D.430°
13.下列关于三角形分类不正确的是(整个大方框表示全体三角形)( )
A.
B.
C.
D.
14.一张△ABC纸片,点M、N分别是AB、AC上的点,若沿直线MN折叠后,点A落在AC边的下面A′的位置,如图所示.则∠1,∠2,∠A之间的数量关系是( )
A.∠1=∠2+∠A
B.∠1=2∠2+∠A
C.∠1=∠2+2∠A
D.∠1=2∠2+2∠A
15.如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2
B.∠3=∠4
C.∠B=∠DCE
D.∠D+∠DAB=180°
16.如图,BD平分∠ABC,若∠1=∠2,则( )
A.AB∥CD
B.AD∥BC
C.AD=BC
D.AB=CD
17.如图,在五边形ABCDE中,AB∥CD,∠A=135°,∠C=60°,∠D=150°,则∠E的大小为( )
A.60°
B.65°
C.70°
D.75°
18.如图,能判定AB∥EF的条件是( )
A.∠ABD=∠FEC
B.∠ABC=∠FEC
C.∠DBC=∠FEB
D.∠DBC=∠FEC
19.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90°
B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180°
D.∠α+∠β+∠γ=180°
20.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A
B.∠1=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180°
参考答案
1.解:过C作CM∥AB,
∵AB∥DE,
∴AB∥CM∥DE,
∴∠1+∠B=180°,∠2=∠D=35°,
∵∠B=130°,
∴∠1=50°,
∴∠BCD=∠1+∠2=85°,
故选:B.
2.解:如图所示:
∵∠2+∠3+∠4=180°,
∠4=90°,∠2=40°,
∴∠3=50°,
又∵a∥b,
∴∠1=∠3,
∴∠1=50°,
故选:B.
3.解:如图所示:
∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴AB∥CD,
∴∠B+∠D=180°,
又∵∠D=50°,
∴∠B=130°,
故选:D.
4.解:∵∠BAC=70°,AF平分∠BAC,
∴∠FAC=∠BAC=35°,
∵DF∥AC,
∴∠1=∠FAC=35°,
故选:B.
5.解:如图知∠A和∠B的关系是相等或互补.
故选:D.
6.解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
故选:C.
7.解:∵∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,即6∠A=180°,
∴∠A=30°,
∴∠B=60°,∠C=90°,
∴△ABC为直角三角形.
故选:B.
8.解:如图,∠2=90°﹣45°=45°,
由三角形的外角性质得,∠1=∠2+60°,
=45°+60°,
=105°.
故选:B.
9.解:∵AB∥CD,
∴∠BMD=∠B=50°,
又∵∠BMD是△CDE的外角,
∴∠E=∠BMD﹣∠D=50°﹣20°=30°.
故选:B.
10.
解:∵∠DPF=∠BMF
∴AB∥CD(同位角相等,两直线平行).
故选:C.
11.解:当∠1=∠2时,EF∥AC;
当∠4=∠C时,EF∥AC;
当∠1+∠3=180°时,DE∥BC;
当∠3+∠C=180°时,EF∥AC;
故选:C.
12.解:∵∠1=70°,
∴∠AED=110°,
∴∠A+∠B+∠C+∠D=540°﹣∠AED=430°.
故选:D.
13.解:根据选项,可知根据角和边来对三角形分别进行分类.
故选:C.
14.解:如图:
由折叠得:∠A=∠A′,
∵∠1是△MDA的外角,
∴∠1=∠A+∠MDA,
同理:∠MDA=∠2+∠A′,
∴∠1=∠A+∠2+∠A′,
即:∠1=2∠A+∠2,
故选:C.
15.解:∵∠1=∠2,
∴AB∥CD,故A能判定AB∥CD;
∵∠3=∠4,
∴AD∥BC,故B不能判定;
∵∠B=∠DCE,
∴AB∥CD,故C能判定;
∵∠D+∠DAB=180°,
∴AB∥CD,故D能判定;
故选:B.
16.解:∵BD平分∠ABC,
∴∠1=∠3,
又∵∠1=∠2,
∴∠2=∠3,
∴AD∥BC(内错角相等,两直线平行).
故选:B.
17.解:∵AB∥CD,
∴∠C+∠B=180°,
∵五边形ABCDE中,∠A=135°,∠D=150°,
∴∠E=540°﹣180°﹣135°﹣150°=75°.
故选:D.
18.解:A、当∠ABD=∠FEC,无法判定AB∥EF,故选项错误;
B、当∠ABC=∠FEC时,AB∥EF,故选项正确;
C、当∠DBC=∠FEB时,无法判定AB∥EF,故选项错误;
D、当∠DBC=∠FEC时,BD∥EF,故选项错误.
故选:B.
19.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
20.解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
《平面图形的认识》
选择题培优(一)
1.如图,若AB∥DE,∠B=130°,∠D=35°,则∠C的度数为( )
A.80°
B.85°
C.90°
D.95°
2.将一个直角三角板与两边平行的纸条按如图所示的方式放置,若∠2=40°,则∠1的大小是( )
A.40°
B.50°
C.60°
D.70°
3.如图,∠1=∠2,∠D=50°,则∠B的度数为( )
A.50°
B.40°
C.100°
D.130°
4.AF是∠BAC的平分线,DF∥AC,若∠BAC=70°,则∠1的度数为( )
A.175°
B.35°
C.55°
D.70°
5.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等
B.互余或互补
C.互补
D.相等或互补
6.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.90°
B.135°
C.270°
D.315°
7.适合条件∠A=∠B=∠C的△ABC是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
8.如果将一副三角板按如图方式叠放,那么∠1等于( )
A.120°
B.105°
C.60°
D.45°
9.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20°
B.30°
C.50°
D.70°
10.如图,在平移三角尺画平行线的过程中,理由是( )
A.两直线平行,同位角相等
B.两直线平行,内错角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行
11.如图,下面哪个条件能判断DE∥BC的是( )
A.∠1=∠2
B.∠4=∠C
C.∠1+∠3=180°
D.∠3+∠C=180°
12.如图,∠1是五边形ABCDE的一个外角.若∠1=70°,则∠A+∠B+∠C+∠D等于( )
A.610°
B.470°
C.290°
D.430°
13.下列关于三角形分类不正确的是(整个大方框表示全体三角形)( )
A.
B.
C.
D.
14.一张△ABC纸片,点M、N分别是AB、AC上的点,若沿直线MN折叠后,点A落在AC边的下面A′的位置,如图所示.则∠1,∠2,∠A之间的数量关系是( )
A.∠1=∠2+∠A
B.∠1=2∠2+∠A
C.∠1=∠2+2∠A
D.∠1=2∠2+2∠A
15.如图,点E在BC的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2
B.∠3=∠4
C.∠B=∠DCE
D.∠D+∠DAB=180°
16.如图,BD平分∠ABC,若∠1=∠2,则( )
A.AB∥CD
B.AD∥BC
C.AD=BC
D.AB=CD
17.如图,在五边形ABCDE中,AB∥CD,∠A=135°,∠C=60°,∠D=150°,则∠E的大小为( )
A.60°
B.65°
C.70°
D.75°
18.如图,能判定AB∥EF的条件是( )
A.∠ABD=∠FEC
B.∠ABC=∠FEC
C.∠DBC=∠FEB
D.∠DBC=∠FEC
19.如图,直线AB∥CD∥EF,点O在直线EF上,下列结论正确的是( )
A.∠α+∠β﹣∠γ=90°
B.∠α+∠γ﹣∠β=180°
C.∠γ+∠β﹣∠α=180°
D.∠α+∠β+∠γ=180°
20.如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A.∠3=∠A
B.∠1=∠2
C.∠D=∠DCE
D.∠D+∠ACD=180°
参考答案
1.解:过C作CM∥AB,
∵AB∥DE,
∴AB∥CM∥DE,
∴∠1+∠B=180°,∠2=∠D=35°,
∵∠B=130°,
∴∠1=50°,
∴∠BCD=∠1+∠2=85°,
故选:B.
2.解:如图所示:
∵∠2+∠3+∠4=180°,
∠4=90°,∠2=40°,
∴∠3=50°,
又∵a∥b,
∴∠1=∠3,
∴∠1=50°,
故选:B.
3.解:如图所示:
∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴AB∥CD,
∴∠B+∠D=180°,
又∵∠D=50°,
∴∠B=130°,
故选:D.
4.解:∵∠BAC=70°,AF平分∠BAC,
∴∠FAC=∠BAC=35°,
∵DF∥AC,
∴∠1=∠FAC=35°,
故选:B.
5.解:如图知∠A和∠B的关系是相等或互补.
故选:D.
6.解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
故选:C.
7.解:∵∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,即6∠A=180°,
∴∠A=30°,
∴∠B=60°,∠C=90°,
∴△ABC为直角三角形.
故选:B.
8.解:如图,∠2=90°﹣45°=45°,
由三角形的外角性质得,∠1=∠2+60°,
=45°+60°,
=105°.
故选:B.
9.解:∵AB∥CD,
∴∠BMD=∠B=50°,
又∵∠BMD是△CDE的外角,
∴∠E=∠BMD﹣∠D=50°﹣20°=30°.
故选:B.
10.
解:∵∠DPF=∠BMF
∴AB∥CD(同位角相等,两直线平行).
故选:C.
11.解:当∠1=∠2时,EF∥AC;
当∠4=∠C时,EF∥AC;
当∠1+∠3=180°时,DE∥BC;
当∠3+∠C=180°时,EF∥AC;
故选:C.
12.解:∵∠1=70°,
∴∠AED=110°,
∴∠A+∠B+∠C+∠D=540°﹣∠AED=430°.
故选:D.
13.解:根据选项,可知根据角和边来对三角形分别进行分类.
故选:C.
14.解:如图:
由折叠得:∠A=∠A′,
∵∠1是△MDA的外角,
∴∠1=∠A+∠MDA,
同理:∠MDA=∠2+∠A′,
∴∠1=∠A+∠2+∠A′,
即:∠1=2∠A+∠2,
故选:C.
15.解:∵∠1=∠2,
∴AB∥CD,故A能判定AB∥CD;
∵∠3=∠4,
∴AD∥BC,故B不能判定;
∵∠B=∠DCE,
∴AB∥CD,故C能判定;
∵∠D+∠DAB=180°,
∴AB∥CD,故D能判定;
故选:B.
16.解:∵BD平分∠ABC,
∴∠1=∠3,
又∵∠1=∠2,
∴∠2=∠3,
∴AD∥BC(内错角相等,两直线平行).
故选:B.
17.解:∵AB∥CD,
∴∠C+∠B=180°,
∵五边形ABCDE中,∠A=135°,∠D=150°,
∴∠E=540°﹣180°﹣135°﹣150°=75°.
故选:D.
18.解:A、当∠ABD=∠FEC,无法判定AB∥EF,故选项错误;
B、当∠ABC=∠FEC时,AB∥EF,故选项正确;
C、当∠DBC=∠FEB时,无法判定AB∥EF,故选项错误;
D、当∠DBC=∠FEC时,BD∥EF,故选项错误.
故选:B.
19.解:∵AB∥EF,
∴∠α=∠BOF,
∵CD∥EF,
∴∠γ+∠COF=180°,
∵∠BOF=∠COF+∠β,
∴∠γ+∠α﹣∠β=180°,
故选:B.
20.解:A、∠3=∠A,无法得到,AB∥CD,故此选项错误;
B、∠1=∠2,根据内错角相等,两直线平行可得:AB∥CD,故此选项正确;
C、∠D=∠DCE,根据内错角相等,两直线平行可得:BD∥AC,故此选项错误;
D、∠D+∠ACD=180°,根据同旁内角互补,两直线平行可得:BD∥AC,故此选项错误;
故选:B.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
