2.5 一元一次不等式与一次函数同步练习(Word版 含答案)
文档属性
| 名称 | 2.5 一元一次不等式与一次函数同步练习(Word版 含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 282.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览



文档简介
2.6一元一次不等式与一次函数
一、单选题
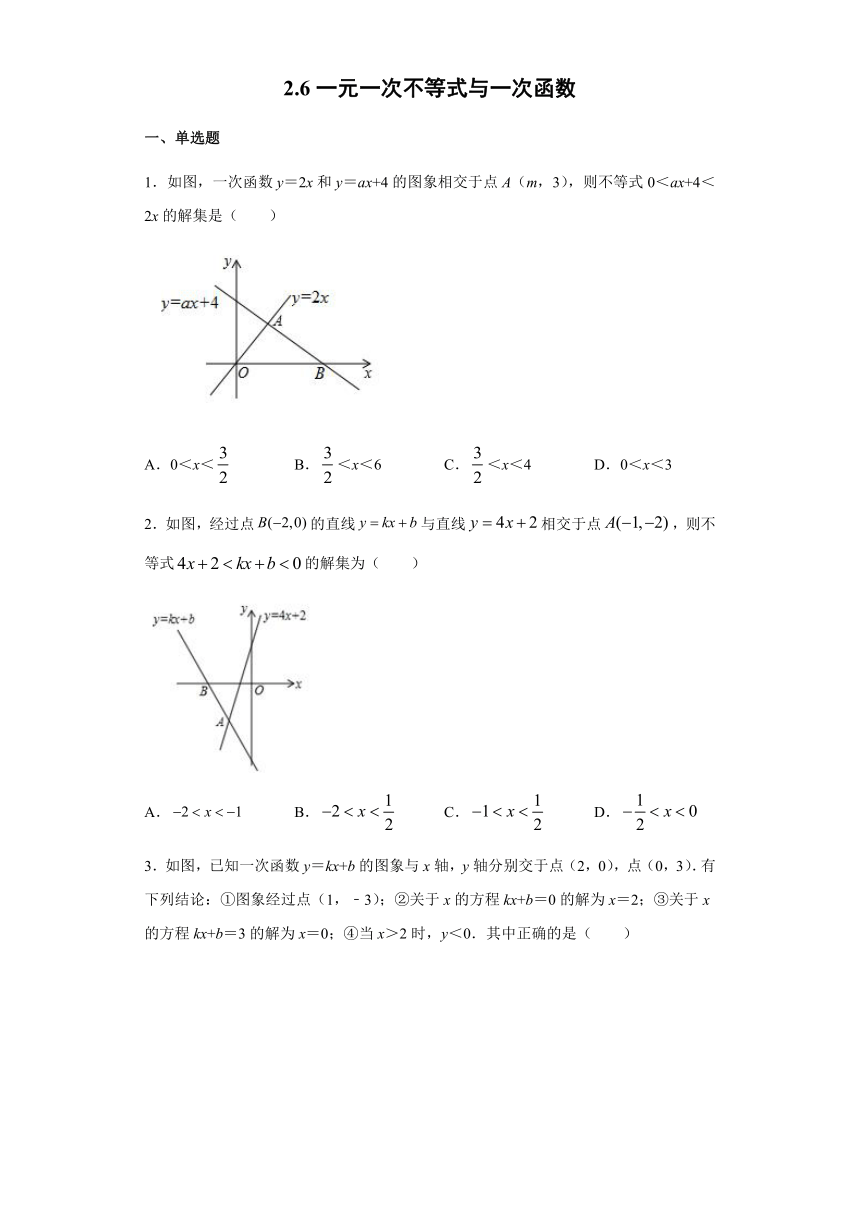
1.如图,一次函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式0<ax+4<2x的解集是( )
A.0<x<false B.false<x<6 C.false<x<4 D.0<x<3
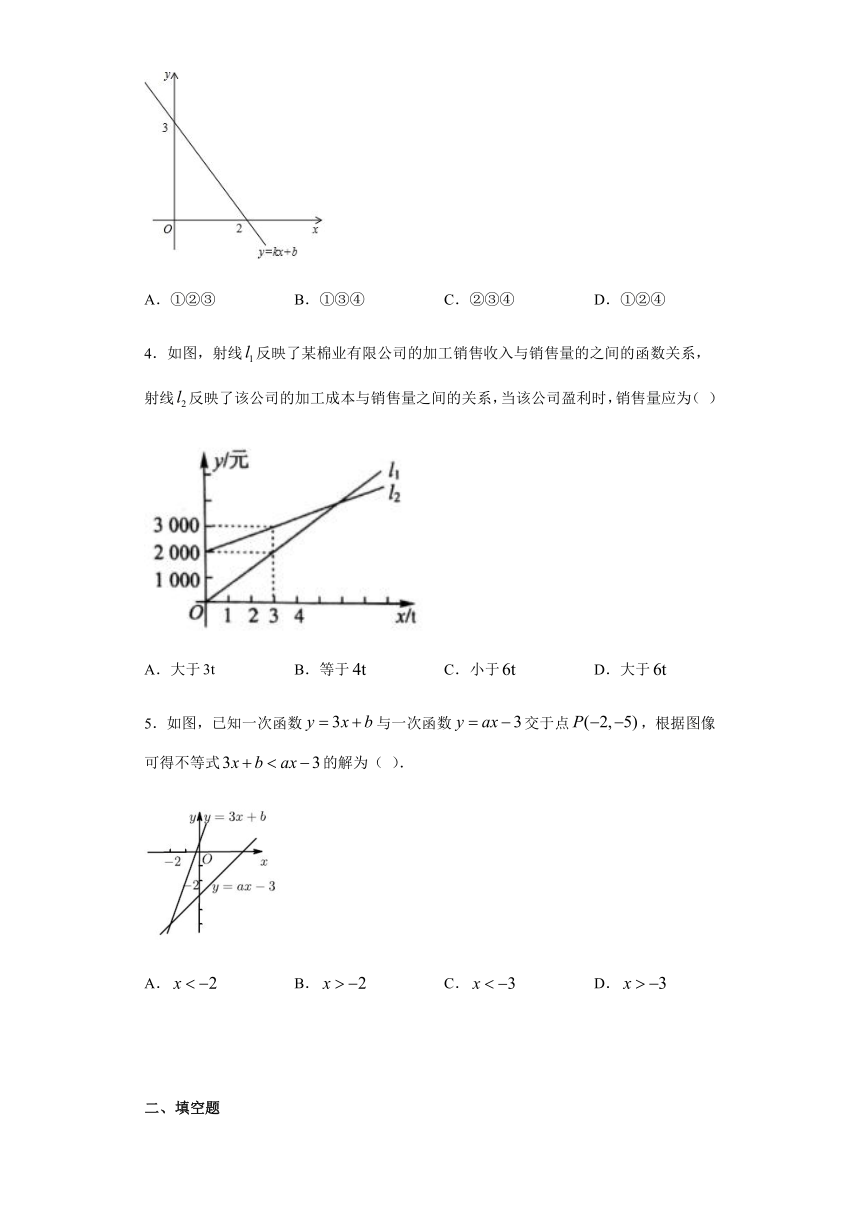
2.如图,经过点false的直线false与直线false相交于点false,则不等式false的解集为( )
A.false B.false C.false D.false
3.如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①图象经过点(1,﹣3);②关于x的方程kx+b=0的解为x=2;③关于x的方程kx+b=3的解为x=0;④当x>2时,y<0.其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
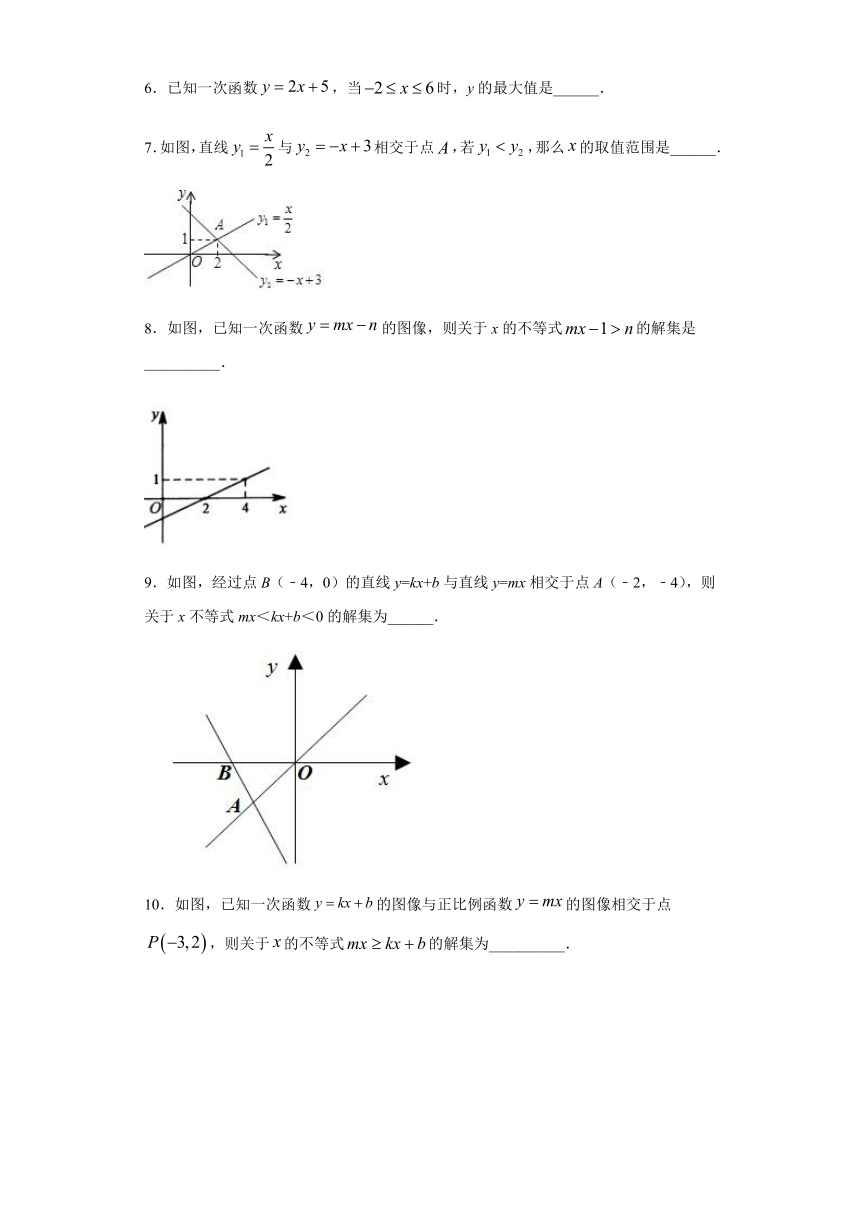
4.如图,射线false反映了某棉业有限公司的加工销售收入与销售量的之间的函数关系,射线false反映了该公司的加工成本与销售量之间的关系,当该公司盈利时,销售量应为( )
A.大于false B.等于false C.小于false D.大于false
5.如图,已知一次函数false与一次函数false交于点false,根据图像可得不等式false的解为( ).
A.false B.false C.false D.false
二、填空题
6.已知一次函数false,当false时,y的最大值是______.
7.如图,直线false与false相交于点false,若false,那么false的取值范围是______.
8.如图,已知一次函数false的图像,则关于x的不等式false的解集是__________.
9.如图,经过点B(﹣4,0)的直线y=kx+b与直线y=mx相交于点A(﹣2,﹣4),则关于x不等式mx<kx+b<0的解集为______.
10.如图,已知一次函数false的图像与正比例函数false的图像相交于点false,则关于false的不等式false的解集为__________.
11.如图,一次函数false与false的图象交于点P.下列结论中,所有正确结论的序号是_________.
①false;②false;③当false时,false;④false;⑤false.
三、解答题
12.已知点P(m,n)在一次函数y=2x﹣3的图象上,且m>2n,求m的取值范围.
13.在平面直角坐标系中,一次函数false(k,b是常数,且false)的图象经过点false和false.
(1)求该函数的表达式;
(2)若点false在该函数的图象上,求点P的坐标;
(3)当false时,求x的取值范围.
14.如图,一次函数false的图像与false轴交于点false;一次函数false的图像与false轴交于点false,且经过点false,两函数图像交于点false.
(1)求false,false,false的值;
(2)根据图象,直接写出false的解集.
15.如图,在平面直角坐标系中,一次函数y=﹣x+n图象与正比例函数y=2x的图象交于点A(m,4).
(1)求m,n的值;
(2)设一次函数y=﹣x+n的图象与x轴交于点B,与y轴交于点C,求点B,点C的坐标;
(3)直接写出使函数y=﹣x+n的值小于函数y=2x的值的自变量x的取值范围.
(4)在x轴上是否存在点P使△PAB为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
16.如图,一次函数false的图象经过点false,与x轴交于点B,与正比例函数false的图象交于点C,点C的横坐标为1
(1)求AB的函数表达式;
(2)若点D在y轴负半轴,且满足false,求点D的坐标;
(3)若false,请直接写出x的取值范围.
参考答案
1.B
2.A
3.C
4.D
5.A
6.17
7.x<2
8.false
9.false
10.false
11.②④⑤
12.false<false
【详解】
解:false 点P(m,n)在一次函数y=2x﹣3的图象上,
false
false m>2n,
false>false
false>false
false<false
false<false
13.(1)false;(2)false;(3)false.
【详解】
解:(1)一次函数false过(2,1)和(-1,7),
∴false,
解得:false,
∴false;
(2)由(1)可知:false,
将false代入false,
∴false,解得false,
即false,
∴false;
(3)∵false,
当false时,
则false,
解得:false,
∴x的取值范围:false.
14.(1)m=2;k=-1;b=4;(2)2<x<3
【详解】
解:(1)false点false在直线false上,
false,
解得false;
false点false、false在直线false上,
falsefalse,
解得:false;
(2)由图象可得,不等式组false的解集为false.
15.(1)m=2,n=6;(2)点B坐标为(6,0),点C坐标为(0,6);(3)x>2;(4)存在,点P坐标为(6+4false,0)或(6﹣4false,0)或(﹣2,0)或(2,0)
【详解】
解:(1)正比例函数y=2x的图象过点A(m,4).
∴4=2m,
∴m=2.
又∵一次函数y=﹣x+n的图象过点A(2,4).
∴4=﹣2+n,
∴n=6.
(2)一次函数y=﹣x+n的图象与x轴交于点B,
∴令y=0,则0=﹣x+6
∴x=6,
∴点B坐标为(6,0),
令x=0,则y=6,
∴点C坐标为(0,6);
(3)由图象可知,在交点A的右侧,函数y=﹣x+n的值小于函数y=2x的值,此时自变量的取值范围是:x>2;
(4)∵点A(2,4),点B坐标为(6,0),
∴AB=false,
当AB=BP=4false时,则点P(6+4false,0)或(6﹣4false,0);
当AB=AP时,如图,过点A作AE⊥BO于E,则点E(2,0),
∵AB=AP,AE⊥BO,
∴PE=BE=4,
∴点P(﹣2,0);
当PA=PB时,
∴∠PBA=∠PAB=45°,
∴∠APB=90°,
∴点P(2,0),
综上所述:点P坐标为(6+4false,0)或(6﹣4false,0)或(﹣2,0)或(2,0).
16.(1)y=-x+4;(2)D(0,-4);(3)x>1.
【详解】
(1)当x=1时,y=3x=3,
∴点C(1,3),
∵直线y=kx+b经过点A(-1,5),C(1,3),
∴false,
解得false,
故AB的函数表达式为y=-x+4;
(2)∵y=-x+4与x轴交于点B,∴B(4,0),
∴false=false=false=6,
∵false=false,∴false=2,
∴false=false=2,
∴OD=4,
故D(0,-4);
(3)根据图像,得x>1.
一、单选题
1.如图,一次函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式0<ax+4<2x的解集是( )
A.0<x<false B.false<x<6 C.false<x<4 D.0<x<3
2.如图,经过点false的直线false与直线false相交于点false,则不等式false的解集为( )
A.false B.false C.false D.false
3.如图,已知一次函数y=kx+b的图象与x轴,y轴分别交于点(2,0),点(0,3).有下列结论:①图象经过点(1,﹣3);②关于x的方程kx+b=0的解为x=2;③关于x的方程kx+b=3的解为x=0;④当x>2时,y<0.其中正确的是( )
A.①②③ B.①③④ C.②③④ D.①②④
4.如图,射线false反映了某棉业有限公司的加工销售收入与销售量的之间的函数关系,射线false反映了该公司的加工成本与销售量之间的关系,当该公司盈利时,销售量应为( )
A.大于false B.等于false C.小于false D.大于false
5.如图,已知一次函数false与一次函数false交于点false,根据图像可得不等式false的解为( ).
A.false B.false C.false D.false
二、填空题
6.已知一次函数false,当false时,y的最大值是______.
7.如图,直线false与false相交于点false,若false,那么false的取值范围是______.
8.如图,已知一次函数false的图像,则关于x的不等式false的解集是__________.
9.如图,经过点B(﹣4,0)的直线y=kx+b与直线y=mx相交于点A(﹣2,﹣4),则关于x不等式mx<kx+b<0的解集为______.
10.如图,已知一次函数false的图像与正比例函数false的图像相交于点false,则关于false的不等式false的解集为__________.
11.如图,一次函数false与false的图象交于点P.下列结论中,所有正确结论的序号是_________.
①false;②false;③当false时,false;④false;⑤false.
三、解答题
12.已知点P(m,n)在一次函数y=2x﹣3的图象上,且m>2n,求m的取值范围.
13.在平面直角坐标系中,一次函数false(k,b是常数,且false)的图象经过点false和false.
(1)求该函数的表达式;
(2)若点false在该函数的图象上,求点P的坐标;
(3)当false时,求x的取值范围.
14.如图,一次函数false的图像与false轴交于点false;一次函数false的图像与false轴交于点false,且经过点false,两函数图像交于点false.
(1)求false,false,false的值;
(2)根据图象,直接写出false的解集.
15.如图,在平面直角坐标系中,一次函数y=﹣x+n图象与正比例函数y=2x的图象交于点A(m,4).
(1)求m,n的值;
(2)设一次函数y=﹣x+n的图象与x轴交于点B,与y轴交于点C,求点B,点C的坐标;
(3)直接写出使函数y=﹣x+n的值小于函数y=2x的值的自变量x的取值范围.
(4)在x轴上是否存在点P使△PAB为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
16.如图,一次函数false的图象经过点false,与x轴交于点B,与正比例函数false的图象交于点C,点C的横坐标为1
(1)求AB的函数表达式;
(2)若点D在y轴负半轴,且满足false,求点D的坐标;
(3)若false,请直接写出x的取值范围.
参考答案
1.B
2.A
3.C
4.D
5.A
6.17
7.x<2
8.false
9.false
10.false
11.②④⑤
12.false<false
【详解】
解:false 点P(m,n)在一次函数y=2x﹣3的图象上,
false
false m>2n,
false>false
false>false
false<false
false<false
13.(1)false;(2)false;(3)false.
【详解】
解:(1)一次函数false过(2,1)和(-1,7),
∴false,
解得:false,
∴false;
(2)由(1)可知:false,
将false代入false,
∴false,解得false,
即false,
∴false;
(3)∵false,
当false时,
则false,
解得:false,
∴x的取值范围:false.
14.(1)m=2;k=-1;b=4;(2)2<x<3
【详解】
解:(1)false点false在直线false上,
false,
解得false;
false点false、false在直线false上,
falsefalse,
解得:false;
(2)由图象可得,不等式组false的解集为false.
15.(1)m=2,n=6;(2)点B坐标为(6,0),点C坐标为(0,6);(3)x>2;(4)存在,点P坐标为(6+4false,0)或(6﹣4false,0)或(﹣2,0)或(2,0)
【详解】
解:(1)正比例函数y=2x的图象过点A(m,4).
∴4=2m,
∴m=2.
又∵一次函数y=﹣x+n的图象过点A(2,4).
∴4=﹣2+n,
∴n=6.
(2)一次函数y=﹣x+n的图象与x轴交于点B,
∴令y=0,则0=﹣x+6
∴x=6,
∴点B坐标为(6,0),
令x=0,则y=6,
∴点C坐标为(0,6);
(3)由图象可知,在交点A的右侧,函数y=﹣x+n的值小于函数y=2x的值,此时自变量的取值范围是:x>2;
(4)∵点A(2,4),点B坐标为(6,0),
∴AB=false,
当AB=BP=4false时,则点P(6+4false,0)或(6﹣4false,0);
当AB=AP时,如图,过点A作AE⊥BO于E,则点E(2,0),
∵AB=AP,AE⊥BO,
∴PE=BE=4,
∴点P(﹣2,0);
当PA=PB时,
∴∠PBA=∠PAB=45°,
∴∠APB=90°,
∴点P(2,0),
综上所述:点P坐标为(6+4false,0)或(6﹣4false,0)或(﹣2,0)或(2,0).
16.(1)y=-x+4;(2)D(0,-4);(3)x>1.
【详解】
(1)当x=1时,y=3x=3,
∴点C(1,3),
∵直线y=kx+b经过点A(-1,5),C(1,3),
∴false,
解得false,
故AB的函数表达式为y=-x+4;
(2)∵y=-x+4与x轴交于点B,∴B(4,0),
∴false=false=false=6,
∵false=false,∴false=2,
∴false=false=2,
∴OD=4,
故D(0,-4);
(3)根据图像,得x>1.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
