8.1.1 二元一次方程 课件 (63张)
文档属性
| 名称 | 8.1.1 二元一次方程 课件 (63张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 12:05:00 | ||
图片预览











文档简介
(共63张PPT)
第八章
8.1.1
二元一次方程
人教版数学七年级下册
1.了解二元一次方程及其解等有关概念,并会判断一组数是不是某个二元一次方程的解.
2.通过对实际问题的分析,进一步体会方程是刻画现实世界的有效数学模型。
学习目标
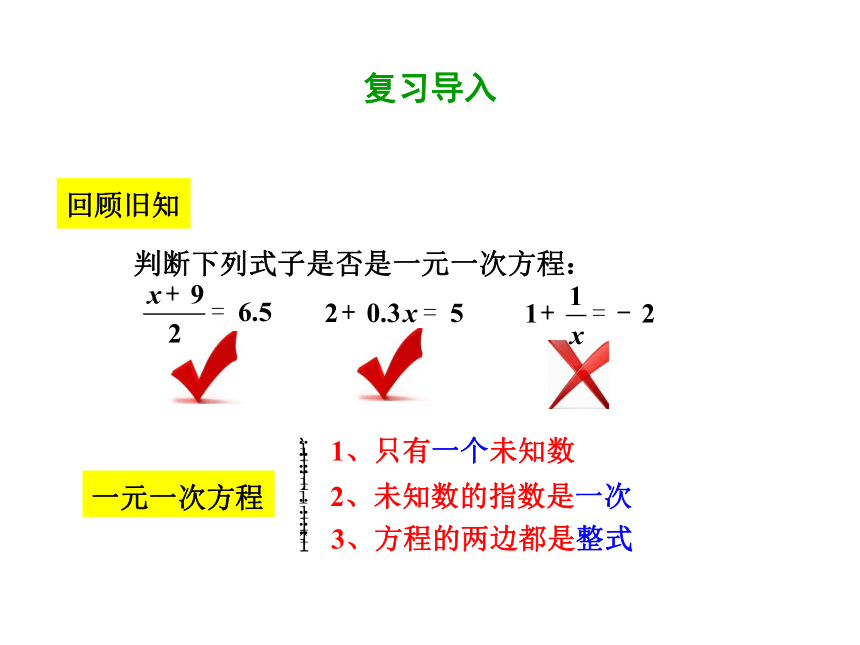
判断下列式子是否是一元一次方程:
回顾旧知
一元一次方程
1、只有一个未知数
2、未知数的指数是一次
3、方程的两边都是整式
复习导入
1
知识点
二元一次方程
思考
引言中的问题包含了哪些必须同时满足的条件?
设胜的场数是x,负的场数是y,你能用方程把这些
条件表示出来吗?
合作探究
由问题知道,题中包含两个必须同时满足的条件:
胜的场数+负的场数=总场数,
胜场积分+负场积分=总积分.
这两个条件可以用方程
x
+
y
=10,
2x
+
y
=
16
表示.
想一想:
上面问题中,我们分别得到方程x
+
y
=10,
2x
+
y
=
16.这些方程各含有几个未知数?
含未知数的项的次数是多少?
1、只含有两个未知数
2、未知数的最高次数是1次
可以发现
3、方程的两边必须是整式
二元
一次
整式方程
含有两个未知数,并且所含未知数的项的
次数都是1的方程叫做二元一次方程.
定义
(1)二元一次方程的条件:
①整式方程;
②只含两个未知数;
③两个未知数系数都不为0;
④含有未知数的项的次数都是1.
(2)二元一次方程的一般形式:ax+by=c(a≠0,
b≠0).
有下列方程:①xy
=1;
②2x=3y;
③
④x2+y=3;
⑤
⑥ax2+2x+3y=0
(a=0),其中,二元一次方程有( )
A.1个
B.2个
C.3个
D.4个
根据二元一次方程的定义,①含未知数的项xy的次
数是2;③不是整式方程;④含未知数的项x2,y中,
x2的次数不是1.只有②⑤⑥满足.其中⑥已指明
a=0,所以ax2=0,则方程化简后为2x+3y=0.
C
例1
导引:
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都
不为0且含未知数的项的次数都是1.
新知小结
例2
(1)已知方程(a+2)x+(b-3)y=9是关于x,y的
二元一次方程,则a的取值范围是________,
b的取值范围是________;
(1)因为方程(a+2)x+(b-3)y=9是关于x,y的
二元一次方程,所以a+2≠0,b-3≠0,所
以a≠-2,b≠3;
a≠-2
b≠3
导引:
合作探究
(2)已知xm-2-yn+1=99是关于x,y的二元一次
方程,则m=____,n=____.
(2)因为xm-2-yn+1=99是关于x,y的二元一次
方程,所以m-2=1,n+1=1,所以m=3,
n=0.
3
0
导引:
在含有字母参数的方程中,如果指明它是二元一次方程,那么它必定隐含两个条件:
(1)含未知数的项的次数都是1;
(2)两个未知数的系数都不为0,根据这两个条件,可
分别得到关于字母参数的方程或不等式(下章将学
到),由此可求得字母参数的值或取值范围.
新知小结
1
在下列式子:①
②
③3x+
y2-2=0;④x=y;⑤x+y-z-1=8;
⑥2xy+
9=0中,是二元一次方程的是_____.(填序号)
①
④
巩固新知
2
下列各式中,是二元一次方程的是( )
A.x-4=y2
B.4x+y=6z
C.
+1=y
D.5x-2y=19
D
3
若xa+2+yb-1=-3是关于x,y的二元一次方程,则a,b应满足( )
A.a=1,b=1
B.a=-1,b=1
C.a=-1,b=2
D.a=1,b=2
C
4
方程(m2-9)x2+x-(m+3)y=0是关于x,y的二元一次方程,则m的值为( )
A.±3
B.3
C.-3
D.9
B
2
知识点
二元一次方程的解
二元一次方程的解:
定义:适合一个二元一次方程的一组未知数的值,
叫做这个二元一次方程的一个解.
合作探究
二元一次方程x-2y=1有无数组解,下列四组值
中不是该方程的解的是(
)
A.
B.
C.
D.
例3
导引:
二元一次方程的解是能使方程两边相等的一对未
知数的值;因此将各个选项逐一代入原方程中,
能使方程左右两边相等,则是方程的解,否则就
不是方程的解.
B
(1)判断一组数值是不是方程的解,可将这组数值分别
代入方程中,若满足该方程,则这组数值就是这个
方程的解,若不满足该方程,则这组数值就不是这
个方程的解;
(2)二元一次方程中,如果已知其中一个未知数的值,
我们可以利用二元一次方程的解的定义求出与它对
应的另一个未知数的值.
新知小结
1
【中考·台湾】x=-3,y=1为下列哪一个二元一次方程的解?( )
A.x+2y=-1
B.x-2y=1
C.2x+3y=6
D.2x-3y=-6
A
巩固新知
2
已知
是方程2x-ay=3的一个解,那么a的值是( )
A.1
B.3
C.-3
D.-1
A
3
如果
是方程x-3y=-3的一组解,那么代数式5-a+3b的值是( )
A.8
B.5
C.2
D.0
A
3
知识点
用含一个未知数的式子表示另一个未知数
二元一次方程x+y=6,
(1)用含有x的代数式表示y为__________;
(2)用含有y的代数式表示x为__________.
合作探究
把方程2x+2y=6改写成用含x的式子表示y的形式,得______________.
本题是将二元一次方程变形,用一个未知数表示另
一个未知数,可先移项,再系数化为1.把方程
2x+2y=6移项得:2y=6-2x,化简:y=3-x.
例4
解析:
y=3-x
用含一个未知数的式子表示另一个未知数的变形
步骤为:
(1)移项,把被表示项移到一边,把其他项移到另
一边;
(2)化系数为1,在方程两边同除以被表示项的系数.
新知小结
1
由
可以得到用x表示y的式子为( )
A.
B.
C.
D.
C
巩固新知
如果2x-7y=8,那么用含y的代数式表示x正确的是( )
A.
B.
C.
D.
2
C
4
知识点
二元一次方程的应用及整数解
例5
求二元一次方程3x+2y=12的非负整数解.
导引:对于二元一次方程3x+2y=12而言,它有无数组
解,但它的非负整数解是有限的,可利用尝试取
值的方法逐个验证.
解:
原方程可化为
因为x,y都是非负整数,
合作探究
所以必须保证12-3x能被2整除,
所以x必为偶数.
而由
所以x=0或2或4.
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0,
所以原方程的非负整数解为
x≥0,得0≤x≤4,
求二元一次方程的整数解的方法:(1)变形:把x看
成常数,把方程变形为用x表示y的形式;(2)划界:根据
方程的解都是整数的特点,划定x的取值范围;(3)试值:
在x的取值范围内逐一试值;(4)确定:根据试值结果得
到二元一次方程的整数解.其求解流程可概述为:
变形
用x表示y
确定x的范围
逐一验证
划界
确定.
试值
新知小结
二元一次方程2x+y=5的正整数解有( )
A.1个
B.2个
C.3个
D.4个
B
1
巩固新知
【中考·龙江】“双11”促销活动中,小芳的妈妈计划用1
000元在唯品会购买价格分别为80元和120元的两种商品,则可供小芳妈妈选择的购买方案有( )
A.4种
B.5种
C.6种
D.7种
2
A
1.
二元一次方程的特征:
(1)是整式方程;
(2)只含有两个未知数;
(3)含有未知数的项的次数都是1;
(4)能整理成ax+by=c的形式,且a≠0,b≠0.
1
知识小结
归纳新知
2.
二元一次方程的解:
(1)二元一次方程的解一般都有无数多个;其整数
解一般是有限个;
(2)每个解都是一对实数,通常用大括号联立.
若(m+2)x|m|-1+y2n+m=5是关于x,y的二元一次方程,
则m=________,n=________.
2
易错小结
2
易错点:忽视二元一次方程定义的隐含条件而致错
由已知方程是二元一次方程可得|m|-1=1,且m
+2≠0,解得m=2;另外,由2n+m=1得n=
.
此题易错之处在于求m的值时,忽略题目中的隐含条件m+2≠0,从而导致m的取值出现两种结果.
1.二元一次方程满足的条件:(1)方程中含有________个未知数,即未知数的系数不能为0;
(2)含有未知数的项的次数都是______;
(3)二元一次方程是________方程,即等式的左右两边必须都是________(分母中不含有未知数).
两
1
整式
整式
课后练习
B
3.方程ax-4y=x-1是二元一次方程,则a的取值为( )
A.a≠0
B.a≠-1
C.a≠1
D.a≠2
C
4.一般地,使二元一次方程两边的值________的两个未知数的值,叫做二元一次方程的解.在二元一次方程中,只要给定其中一个未知数的值,就可以相应地求出另一个未知数的值,因此二元一次方程有________个解,即有无数多对数适合这个二元一次方程.
相等
无数
1
B
6.二元一次方程5a-11b=21( )
A.有且只有一解
B.有无数解
C.无解
D.有且只有两解
【答案】A
A
9.将一个二元一次方程改写成用含一个未知数的式子表示另一个未知数的形式,方法是利用__________的性质将其变形为y=________(或x=________)的形式,其中a,b为常数,a≠0.
等式
ax+b
ay+b
10.11x-9y=6,用含x的整式表示y,得y=________;用含y的整式表示x,得x=__________.
C
12.笼中有x只鸡、y只兔,共有36只脚,能表示其中数量关系的方程是( )
A.x+y=18
B.x+y=36
C.4x+2y=36
D.2x+4y=36
D
13.(2019·天门)把一根9
m长的钢管截成1
m长和2
m长两种规格均有的短钢管,且没有余料,设某种截法中1
m长的钢管有a根,则a的值可能有( )
A.3种
B.4种
C.5种
D.9种
B
14.(2020·齐齐哈尔)母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每枝2元,百合每枝3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )
A.3种
B.4种
C.5种
D.6种
【答案】B
15.已知方程(2m-4)xm+3+(n+3)y|n|-2=6是关于x,y的二元一次方程,试求m,n的值.
解:因为方程(2m-4)xm+3+(n+3)y|n|-2=6是关于x,y的二元一次方程,
所以m+3=1,|n|-2=1,2m-4≠0,n+3≠0.
解得m=-2,n=3.
17.已知方程3x+y=12.
(1)用含x的式子表示y;
解:y=12-3x.
(2)用含y的式子表示x;
(4)写出方程的两个解.
(3)求当x=2时y的值及当y=24时x的值;
解:当x=2时,y的值为6;
当y=24时,x的值为-4.
18.(1)写出二元一次方程x+2y=6的正整数解;
(2)写出二元一次方程2x+3y=15的非负整数解.
【点拨】先利用等式的性质将原方程变形为用一个未知数表示另一个未知数的形式,再尝试代入数值求解.
19.某电视台黄金时段的2
min广告时间内,插播时间分别为15
s和30
s的两种广告,15
s的广告每播1次收费0.6万元,30
s的广告每播1次收费1万元,要求每种广告播放不少于2次.若设15
s的广告播放x次,30
s的广告播放y次.
(1)试写出关于x,y的方程.
【思路点拨】根据“15
s的广告播放x次,30
s的广告播放y次”列二元一次方程;
解:所求方程为15x+30y=120.
(2)两种广告播放的次数有哪几种安排方式?
【思路点拨】实质是求二元一次方程满足条件的解;
∴两种广告播放的次数有两种安排方式:
①15
s的广告播放4次,30
s的广告播放2次;
②15
s的广告播放2次,30
s的广告播放3次.
(3)电视台选择哪种方式播放,利润最大?最大利润是多少?
解:∵按方式①所得利润为0.6×4+1×2=4.4(万元),按方式②所得利润为0.6×2+1×3=4.2(万元),∴按15
s的广告播放4次,30
s的广告播放2次所得的利润最大,最大利润是4.4万元.
【思路点拨】计算几种满足条件的解的利润情况,进行比较即可求出.
再见
第八章
8.1.1
二元一次方程
人教版数学七年级下册
1.了解二元一次方程及其解等有关概念,并会判断一组数是不是某个二元一次方程的解.
2.通过对实际问题的分析,进一步体会方程是刻画现实世界的有效数学模型。
学习目标
判断下列式子是否是一元一次方程:
回顾旧知
一元一次方程
1、只有一个未知数
2、未知数的指数是一次
3、方程的两边都是整式
复习导入
1
知识点
二元一次方程
思考
引言中的问题包含了哪些必须同时满足的条件?
设胜的场数是x,负的场数是y,你能用方程把这些
条件表示出来吗?
合作探究
由问题知道,题中包含两个必须同时满足的条件:
胜的场数+负的场数=总场数,
胜场积分+负场积分=总积分.
这两个条件可以用方程
x
+
y
=10,
2x
+
y
=
16
表示.
想一想:
上面问题中,我们分别得到方程x
+
y
=10,
2x
+
y
=
16.这些方程各含有几个未知数?
含未知数的项的次数是多少?
1、只含有两个未知数
2、未知数的最高次数是1次
可以发现
3、方程的两边必须是整式
二元
一次
整式方程
含有两个未知数,并且所含未知数的项的
次数都是1的方程叫做二元一次方程.
定义
(1)二元一次方程的条件:
①整式方程;
②只含两个未知数;
③两个未知数系数都不为0;
④含有未知数的项的次数都是1.
(2)二元一次方程的一般形式:ax+by=c(a≠0,
b≠0).
有下列方程:①xy
=1;
②2x=3y;
③
④x2+y=3;
⑤
⑥ax2+2x+3y=0
(a=0),其中,二元一次方程有( )
A.1个
B.2个
C.3个
D.4个
根据二元一次方程的定义,①含未知数的项xy的次
数是2;③不是整式方程;④含未知数的项x2,y中,
x2的次数不是1.只有②⑤⑥满足.其中⑥已指明
a=0,所以ax2=0,则方程化简后为2x+3y=0.
C
例1
导引:
判断一个方程是否为二元一次方程的方法:
一看原方程是否是整式方程且只含有两个未知数;
二看整理化简后的方程是否具备两个未知数的系数都
不为0且含未知数的项的次数都是1.
新知小结
例2
(1)已知方程(a+2)x+(b-3)y=9是关于x,y的
二元一次方程,则a的取值范围是________,
b的取值范围是________;
(1)因为方程(a+2)x+(b-3)y=9是关于x,y的
二元一次方程,所以a+2≠0,b-3≠0,所
以a≠-2,b≠3;
a≠-2
b≠3
导引:
合作探究
(2)已知xm-2-yn+1=99是关于x,y的二元一次
方程,则m=____,n=____.
(2)因为xm-2-yn+1=99是关于x,y的二元一次
方程,所以m-2=1,n+1=1,所以m=3,
n=0.
3
0
导引:
在含有字母参数的方程中,如果指明它是二元一次方程,那么它必定隐含两个条件:
(1)含未知数的项的次数都是1;
(2)两个未知数的系数都不为0,根据这两个条件,可
分别得到关于字母参数的方程或不等式(下章将学
到),由此可求得字母参数的值或取值范围.
新知小结
1
在下列式子:①
②
③3x+
y2-2=0;④x=y;⑤x+y-z-1=8;
⑥2xy+
9=0中,是二元一次方程的是_____.(填序号)
①
④
巩固新知
2
下列各式中,是二元一次方程的是( )
A.x-4=y2
B.4x+y=6z
C.
+1=y
D.5x-2y=19
D
3
若xa+2+yb-1=-3是关于x,y的二元一次方程,则a,b应满足( )
A.a=1,b=1
B.a=-1,b=1
C.a=-1,b=2
D.a=1,b=2
C
4
方程(m2-9)x2+x-(m+3)y=0是关于x,y的二元一次方程,则m的值为( )
A.±3
B.3
C.-3
D.9
B
2
知识点
二元一次方程的解
二元一次方程的解:
定义:适合一个二元一次方程的一组未知数的值,
叫做这个二元一次方程的一个解.
合作探究
二元一次方程x-2y=1有无数组解,下列四组值
中不是该方程的解的是(
)
A.
B.
C.
D.
例3
导引:
二元一次方程的解是能使方程两边相等的一对未
知数的值;因此将各个选项逐一代入原方程中,
能使方程左右两边相等,则是方程的解,否则就
不是方程的解.
B
(1)判断一组数值是不是方程的解,可将这组数值分别
代入方程中,若满足该方程,则这组数值就是这个
方程的解,若不满足该方程,则这组数值就不是这
个方程的解;
(2)二元一次方程中,如果已知其中一个未知数的值,
我们可以利用二元一次方程的解的定义求出与它对
应的另一个未知数的值.
新知小结
1
【中考·台湾】x=-3,y=1为下列哪一个二元一次方程的解?( )
A.x+2y=-1
B.x-2y=1
C.2x+3y=6
D.2x-3y=-6
A
巩固新知
2
已知
是方程2x-ay=3的一个解,那么a的值是( )
A.1
B.3
C.-3
D.-1
A
3
如果
是方程x-3y=-3的一组解,那么代数式5-a+3b的值是( )
A.8
B.5
C.2
D.0
A
3
知识点
用含一个未知数的式子表示另一个未知数
二元一次方程x+y=6,
(1)用含有x的代数式表示y为__________;
(2)用含有y的代数式表示x为__________.
合作探究
把方程2x+2y=6改写成用含x的式子表示y的形式,得______________.
本题是将二元一次方程变形,用一个未知数表示另
一个未知数,可先移项,再系数化为1.把方程
2x+2y=6移项得:2y=6-2x,化简:y=3-x.
例4
解析:
y=3-x
用含一个未知数的式子表示另一个未知数的变形
步骤为:
(1)移项,把被表示项移到一边,把其他项移到另
一边;
(2)化系数为1,在方程两边同除以被表示项的系数.
新知小结
1
由
可以得到用x表示y的式子为( )
A.
B.
C.
D.
C
巩固新知
如果2x-7y=8,那么用含y的代数式表示x正确的是( )
A.
B.
C.
D.
2
C
4
知识点
二元一次方程的应用及整数解
例5
求二元一次方程3x+2y=12的非负整数解.
导引:对于二元一次方程3x+2y=12而言,它有无数组
解,但它的非负整数解是有限的,可利用尝试取
值的方法逐个验证.
解:
原方程可化为
因为x,y都是非负整数,
合作探究
所以必须保证12-3x能被2整除,
所以x必为偶数.
而由
所以x=0或2或4.
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0,
所以原方程的非负整数解为
x≥0,得0≤x≤4,
求二元一次方程的整数解的方法:(1)变形:把x看
成常数,把方程变形为用x表示y的形式;(2)划界:根据
方程的解都是整数的特点,划定x的取值范围;(3)试值:
在x的取值范围内逐一试值;(4)确定:根据试值结果得
到二元一次方程的整数解.其求解流程可概述为:
变形
用x表示y
确定x的范围
逐一验证
划界
确定.
试值
新知小结
二元一次方程2x+y=5的正整数解有( )
A.1个
B.2个
C.3个
D.4个
B
1
巩固新知
【中考·龙江】“双11”促销活动中,小芳的妈妈计划用1
000元在唯品会购买价格分别为80元和120元的两种商品,则可供小芳妈妈选择的购买方案有( )
A.4种
B.5种
C.6种
D.7种
2
A
1.
二元一次方程的特征:
(1)是整式方程;
(2)只含有两个未知数;
(3)含有未知数的项的次数都是1;
(4)能整理成ax+by=c的形式,且a≠0,b≠0.
1
知识小结
归纳新知
2.
二元一次方程的解:
(1)二元一次方程的解一般都有无数多个;其整数
解一般是有限个;
(2)每个解都是一对实数,通常用大括号联立.
若(m+2)x|m|-1+y2n+m=5是关于x,y的二元一次方程,
则m=________,n=________.
2
易错小结
2
易错点:忽视二元一次方程定义的隐含条件而致错
由已知方程是二元一次方程可得|m|-1=1,且m
+2≠0,解得m=2;另外,由2n+m=1得n=
.
此题易错之处在于求m的值时,忽略题目中的隐含条件m+2≠0,从而导致m的取值出现两种结果.
1.二元一次方程满足的条件:(1)方程中含有________个未知数,即未知数的系数不能为0;
(2)含有未知数的项的次数都是______;
(3)二元一次方程是________方程,即等式的左右两边必须都是________(分母中不含有未知数).
两
1
整式
整式
课后练习
B
3.方程ax-4y=x-1是二元一次方程,则a的取值为( )
A.a≠0
B.a≠-1
C.a≠1
D.a≠2
C
4.一般地,使二元一次方程两边的值________的两个未知数的值,叫做二元一次方程的解.在二元一次方程中,只要给定其中一个未知数的值,就可以相应地求出另一个未知数的值,因此二元一次方程有________个解,即有无数多对数适合这个二元一次方程.
相等
无数
1
B
6.二元一次方程5a-11b=21( )
A.有且只有一解
B.有无数解
C.无解
D.有且只有两解
【答案】A
A
9.将一个二元一次方程改写成用含一个未知数的式子表示另一个未知数的形式,方法是利用__________的性质将其变形为y=________(或x=________)的形式,其中a,b为常数,a≠0.
等式
ax+b
ay+b
10.11x-9y=6,用含x的整式表示y,得y=________;用含y的整式表示x,得x=__________.
C
12.笼中有x只鸡、y只兔,共有36只脚,能表示其中数量关系的方程是( )
A.x+y=18
B.x+y=36
C.4x+2y=36
D.2x+4y=36
D
13.(2019·天门)把一根9
m长的钢管截成1
m长和2
m长两种规格均有的短钢管,且没有余料,设某种截法中1
m长的钢管有a根,则a的值可能有( )
A.3种
B.4种
C.5种
D.9种
B
14.(2020·齐齐哈尔)母亲节来临,小明去花店为妈妈准备节日礼物.已知康乃馨每枝2元,百合每枝3元.小明将30元钱全部用于购买这两种花(两种花都买),小明的购买方案共有( )
A.3种
B.4种
C.5种
D.6种
【答案】B
15.已知方程(2m-4)xm+3+(n+3)y|n|-2=6是关于x,y的二元一次方程,试求m,n的值.
解:因为方程(2m-4)xm+3+(n+3)y|n|-2=6是关于x,y的二元一次方程,
所以m+3=1,|n|-2=1,2m-4≠0,n+3≠0.
解得m=-2,n=3.
17.已知方程3x+y=12.
(1)用含x的式子表示y;
解:y=12-3x.
(2)用含y的式子表示x;
(4)写出方程的两个解.
(3)求当x=2时y的值及当y=24时x的值;
解:当x=2时,y的值为6;
当y=24时,x的值为-4.
18.(1)写出二元一次方程x+2y=6的正整数解;
(2)写出二元一次方程2x+3y=15的非负整数解.
【点拨】先利用等式的性质将原方程变形为用一个未知数表示另一个未知数的形式,再尝试代入数值求解.
19.某电视台黄金时段的2
min广告时间内,插播时间分别为15
s和30
s的两种广告,15
s的广告每播1次收费0.6万元,30
s的广告每播1次收费1万元,要求每种广告播放不少于2次.若设15
s的广告播放x次,30
s的广告播放y次.
(1)试写出关于x,y的方程.
【思路点拨】根据“15
s的广告播放x次,30
s的广告播放y次”列二元一次方程;
解:所求方程为15x+30y=120.
(2)两种广告播放的次数有哪几种安排方式?
【思路点拨】实质是求二元一次方程满足条件的解;
∴两种广告播放的次数有两种安排方式:
①15
s的广告播放4次,30
s的广告播放2次;
②15
s的广告播放2次,30
s的广告播放3次.
(3)电视台选择哪种方式播放,利润最大?最大利润是多少?
解:∵按方式①所得利润为0.6×4+1×2=4.4(万元),按方式②所得利润为0.6×2+1×3=4.2(万元),∴按15
s的广告播放4次,30
s的广告播放2次所得的利润最大,最大利润是4.4万元.
【思路点拨】计算几种满足条件的解的利润情况,进行比较即可求出.
再见
