2.3平行线的性质课件（31张）

3　平行线的性质第1课时
填空:(1)∵∠1 = ∠2（已知）?
? ∴ BF // CE
（内错角相等，两直线平行 ）
(2) ∵∠2 = ∠M（已知）?
? ∴ AM // BF
（同位角相等，两直线平行 ）
(3) ∵ ∠2 +∠3=180° （已知）?
? ∴ AC // MD
（同旁内角互补，两直线平行 ）
如图：直线a与直线b平行
测量同位角∠1 和∠5 的大小，它们有什么关系？ 图中还有其他同位角吗？它们的大小有什么关系？
∠1=∠5
a∥b
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
性质1:两条平行直线被第三条直线所截, 同位角相等。
简称:两直线平行, 同位角相等.
平行线的性质1(数学基本事实)
性质1:两条平行直线被第三条直线所截, 同位角相等。
简称:两直线平行, 同位角相等.
性质3:两条平行直线被第三条直线所截,同旁内角互补。
简称:两直线平行, 同旁内角互补.
性质2:两条平行直线被第三条直线所截,内错角相等。
简称:两直线平行, 内错角相等.

同位角相等
两直线平行

条件
性质

条件：角的关系 线的关系???????
性质：线的关系 角的关系
平行线的性质与判定平行的条件的区别：
内错角相等
同旁内角互补
3、归纳整理:
符号语言
⑴∵ a∥b ( 已知 )
∴ ∠1=∠5(两直线平行，同位角相等）
∠2=∠6 ∠3=∠7 ∠4=∠8
⑵∵a∥b( 已知 )
∴ ∠6=∠3 ∠4=∠5(两直线平行，内错角相等)
(∠1=∠8 ∠2=∠7 等角的补角相等）
⑶∵a∥b( 已知 )
∴ ∠6+∠4=180°
(两直线平行，同旁内角互补)
∠3+∠5=180°
B
E
1
2
3
4
C
F
D
A
B
E
如图所示，一束平行光线AB与DE射向一个水平镜面后被反射，此时∠1=∠2，∠3= ∠4。
（1）∠1 ，∠3的大小有什么关系？ ∠2与∠4呢？
（2）反射光线BC与EF也平行吗？
做一做
（1） AB // DE
∠1 =∠3
∠1 =∠3
∠1 =∠2
∠3 =∠4
∠2=∠4
（2）
∠2=∠4
BC // EF
B
E
1
2
3
4
C
F
D
A
B
E
如图所示，AB∥CD，AC ∥BD, 分别找出与∠1相等或互补的角.
A
D
C
B
1
6
5
4
3
2
7
8
14
13
15
16
10
9
11
12
如图，与∠1相等的角有：
∠3， ∠5， ∠7， ∠9，
∠11， ∠13， ∠15；
与∠1互补的角有：
∠2， ∠4， ∠6， ∠8，
∠10， ∠12， ∠14， ∠16 .
解：
随堂练习
1、如图，下列推理所注理由正确的是（ ）
A、∵DE∥BC ∴ ∠1= ∠C （同位角相等，两直线平行）
B、∵ ∠2= ∠3 ∴ DE∥BC（内错角相等，两直线平行）
C、∵DE∥BC ∴ ∠2= ∠3 （两直线平行，内错角相等）
D、∵ ∠1= ∠C ∴DE∥BC（两直线平行，同位角相等）
B
C
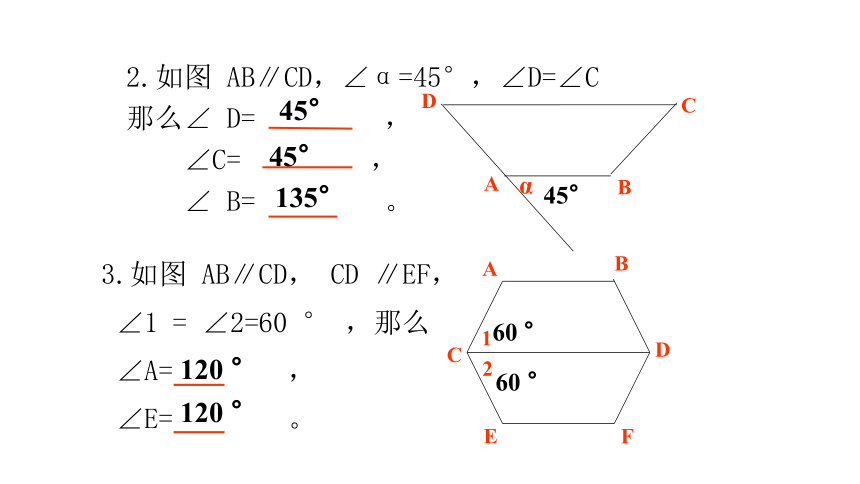
2.如图 AB∥CD，∠α=45°，∠D=∠C
那么∠ D= ，
∠C= ，
∠ B= 。
A
B
C
D
α
45°
60 °
A
B
C
D
E
F
1
2
60 °
3.如图 AB∥CD， CD ∥EF，
∠1 = ∠2=60 ° ，那么
∠A= ，
∠E= 。
45°
45°
135°
120 °
120 °
【练习提高】
1.如图,完成下列填空
(1)∵AB//DC(已知)
∴∠B=∠1
( )
(2)∵AD//BC(已知)
∴______=∠1
( )
A
B
C
D
1


两直线平行，同位角相等
∠D
两直线平行，内错角相等
(3)∵_______//_______(已知)
∴ ∠A+∠B=180° ( )
(4)∵_______//_______(已知)
∴ ∠A+∠D=180°
( )
A
B
C
D
1
AB
BC
AD
DC
两直线平行，同旁内角互补
两直线平行，同旁内角互补
2.下列说法:
①两条直线平行,同旁内角互补;
②同位角相等,两直线平行;
③内错角相等,两直线平行;
④垂直于同一直线的两直线平行,其中是平
行线的性质的是( )
A.① B.②和③ C.④ D.①和④
A
本课小结： 平行线的性质与判定的区别
性质1:两条平行直线被第三条直线所截, 同位角相等。
简称:两直线平行, 同位角相等.
性质3:两条平行直线被第三条直线所截,同旁内角互补。
简称:两直线平行, 同旁内角互补.
性质2:两条平行直线被第三条直线所截,内错角相等。
简称:两直线平行, 内错角相等.
判定1.同位角相等,两直线平行
判定2.内错角相等,两直线平行
判定3.同旁内角互补,两直线平行

【课外作业】 1.看图填空
∵∠1＝∠2
∴ ∥ ，
（内错角相等，两直线平行）
∵∠2＝ ，
∴ ∥ ，
（同位角相等，两直线平行）
∵∠3＋∠4＝180°
∴ ∥ ，
（同旁内角互补，两直线平行）
∴ AC∥FG.
（平行于同一条直线的两条直线平行）
1
2
3
4
A
B
C
D
E
F
G
AC
DE
∠4
DE
BG
DE
BG
2．填写理由：如图，
∵∠A=∠BDE（已知），
∴AC∥DE
（ )
∴∠DEB=∠C
（ ）
∵∠C=90°（已知），
∴∠DEB=90° （ ）
∴DE⊥EB（ ）
同位角相等，两直线平行
两直线平行,同位角相等
等量代换
垂直定义
3　平行线的性质第2课时
例1根据图2--20回答下列问题:
(1)若∠1=∠2,则可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,则可以判定哪两条直线平行?根据是什么?
(3)若∠2+∠3= 180°，则可以判定哪两条直线平行?根据是什么?
解: (1)∠1与∠2是内错角，若∠1=∠2,则根据“内错角相等，两直线平行”，可得BF// CE;
(2)∠2与∠M是同位角，若∠2=∠M，则根据“同位角相等，两直线平行”，可得AM// BF;
(3)∠2与∠3是同旁内角，若∠2+∠3= 180°，则根据“同旁内角互补，两直线平行”，可得AC// MD.
练习1．如图，AE∥CD，若∠1 = 37°，∠D =54°，求∠2 和∠BAE的度数.
解：∵AE∥CD，∠1 = 37° （已知）
∴ ∠2 = ∠1 =37°
（两直线平行，内错角相等）
∵ AE∥CD，∠D =54 °（已知）
∴ ∠BAE = ∠D =54°
（两直线平行，同位角相等） ）
例2.如图所示:AB∥CD,如果∠1=∠2，那么EF与AB平行吗？说说你的理由。
解： ∵∠1 = ∠2 （ ）
∴ EF∥ （ ）
又∵AB∥CD（ ）
∴ ∥ （__________ ）
已知
CD
AB
EF
已知
内错角相等，两直线平行
两直线平行于第三条直线,则这二线平行
练习2.如图, ∠B=∠C ∠B+∠D=180°，
那么BC平行DE吗？为什么？
A
B
C
D
E
解：BC∥DE
理由如下
∵ ∠B=∠C （ ）
已知
∠B+ ∠D=180°（ ）
已知
∴ ∠C+ ∠D=180°（ ）
等量代换
∴BC∥DE（ ）
同旁内角互补，两直线平行
例3: 如图，已知直线 a∥b，
直线 c∥d， ∠1 = 107°，
求 ∠2， ∠3 的度数.

解：∵a//b（已知）?
∴∠2 = ∠1=107°
（两直线平行，内错角相等）
∵c//d（已知）
∴∠1 +∠3=180°
（两直线平行，同旁内角互补 ）
∴∠3= 180°﹣ ∠1 =73°
证明 ：（1）∵AD ∥BE（ ）
∴ ∠3= ∠5 （ ）
又∵AC∥DE（ ）
∴ ∠5= ∠4 （ ）
∴ ∠3= ∠4 （ ）
（2）∵AD∥BE（ ）
∴ ∠1= ∠6 （ ）
又∵ ∠1= ∠2 （ ）
∴ ∠2= ∠6 （ ）
∴AB∥CD （ ）


#k#b#1#新#课#

已知
两直线平行内错角相等
已知
两直线平行同位角相等
等量代换
已知
两直线平行内错角相等
同位角相等两直线平行
等量代换
已知
3、 如图，已知AD∥BE，AC∥DE， ∠1= ∠2 可推出
（1） ∠3= ∠4 （2）AB∥CD。填出推理理由。
1.必做题: 课本54页 习题2.6
1、2、3、4、 6

2.选做题：
如图EF∥AD，∠1=∠2，
∠BAC=70 °，求∠AGD的度数。
布置作业
1.如图,BD平分∠_ABC,点E在BC上,EF// AB.若∠CEF=100°,则∠ABD的度数为（ ）
B
A.60°
B.50°
C.40°
D.30
2.(2018. 自贡中考)如图,若∠1=55°,则∠2的度数是（ ）
A.50°
B.45°
C.40°
D.35°
课外作业
D
3.如图,直线AB//CD,∠1= 65°∠2=50° ,试说明BC平分∠ABD.
4.如图,直线AB//CD，∠EMB= 100° ,MF平分∠AME,交CD于点F ,求∠EFM的大小.
5.如图,AB// DE// GF,∠1 :∠D :∠B=2:3 :4,求∠1的度数.
6.如图,AD//BC,∠EAD=∠C.(1)试说明:AE//CD,
(2)若∠EFC=50° ,∠C=65° ,求∠BEF的度数.
7.如图,已知∠1+∠2= 180°，∠3=∠B,试说明:DE// BC.