六年级数学下册课件-7 总复习-平面图形的周长和面积 -苏教版(共26张PPT)
文档属性
| 名称 | 六年级数学下册课件-7 总复习-平面图形的周长和面积 -苏教版(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 13:58:35 | ||
图片预览

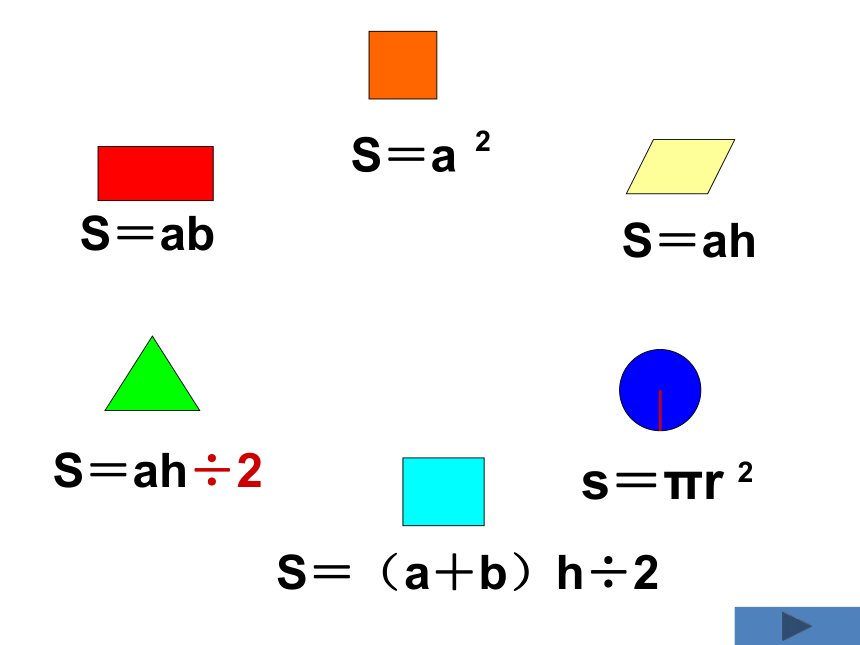
文档简介
(共26张PPT)
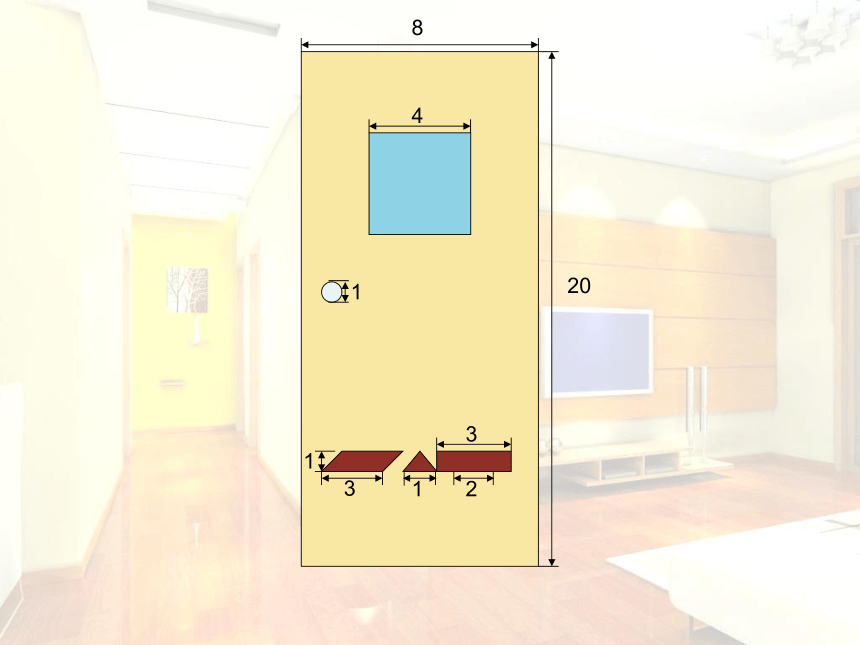
平面图形的面积
1
20
8
4
3
3
2
1
1
S=ab
S=a
2
S=ah
S=ah÷2
S=(a+b)h÷2
s=πr
2
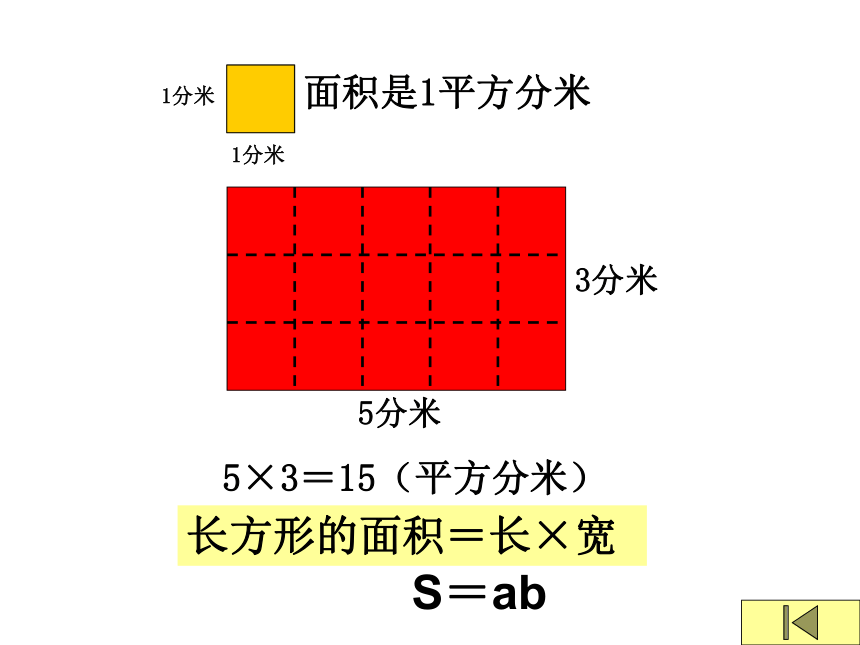
5分米
3分米
1分米
1分米
面积是1平方分米
5×3=15(平方分米)
长方形的面积=长×宽
S=ab
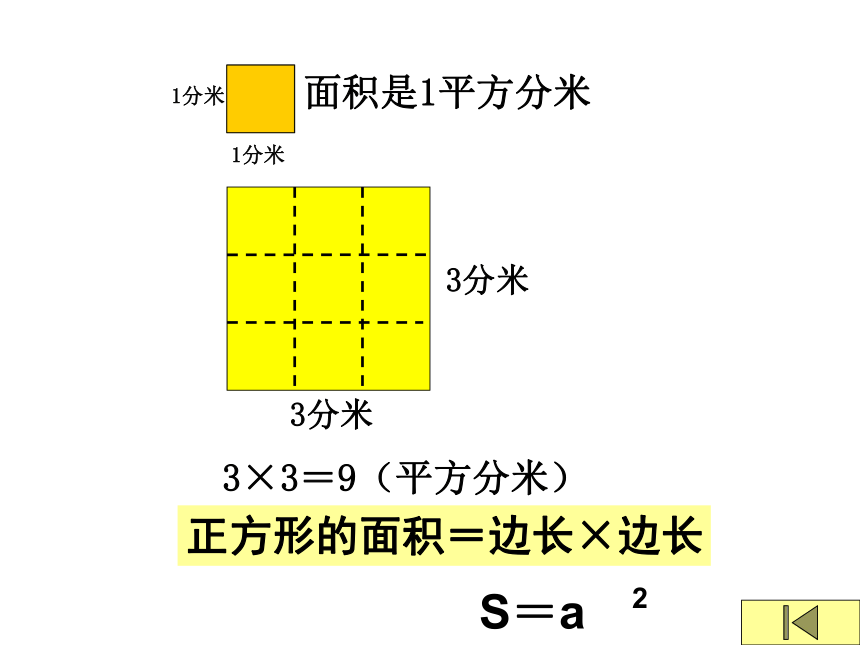
3分米
3分米
1分米
1分米
面积是1平方分米
3×3=9(平方分米)
正方形的面积=边长×边长
S=a
2
底
高
(长)
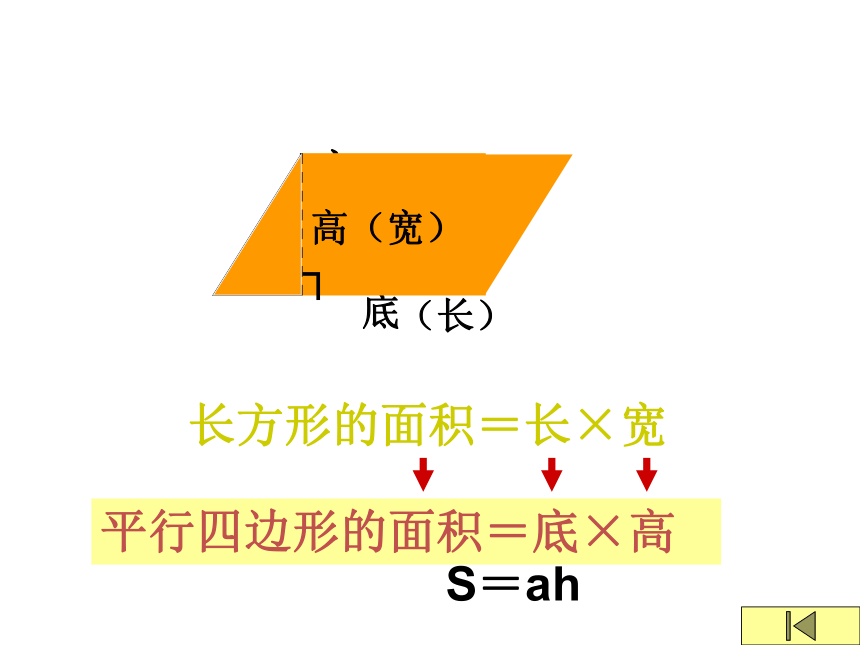
长方形的面积=长×宽
平行四边形的面积=底×高
S=ah
┐
高(宽)
底
┐
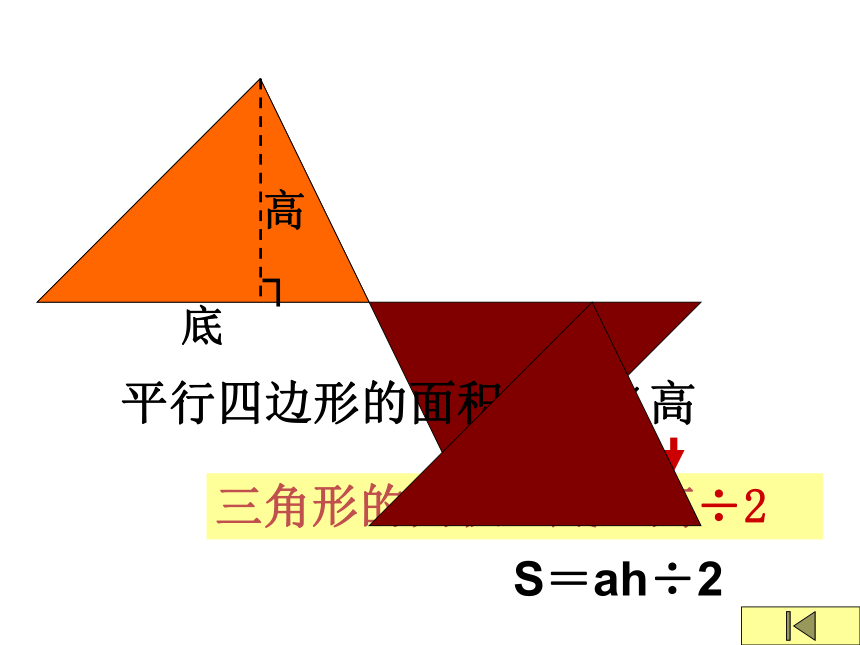
高
平行四边形的面积=底×高
三角形的面积=底×高÷2
S=ah÷2
高
┐
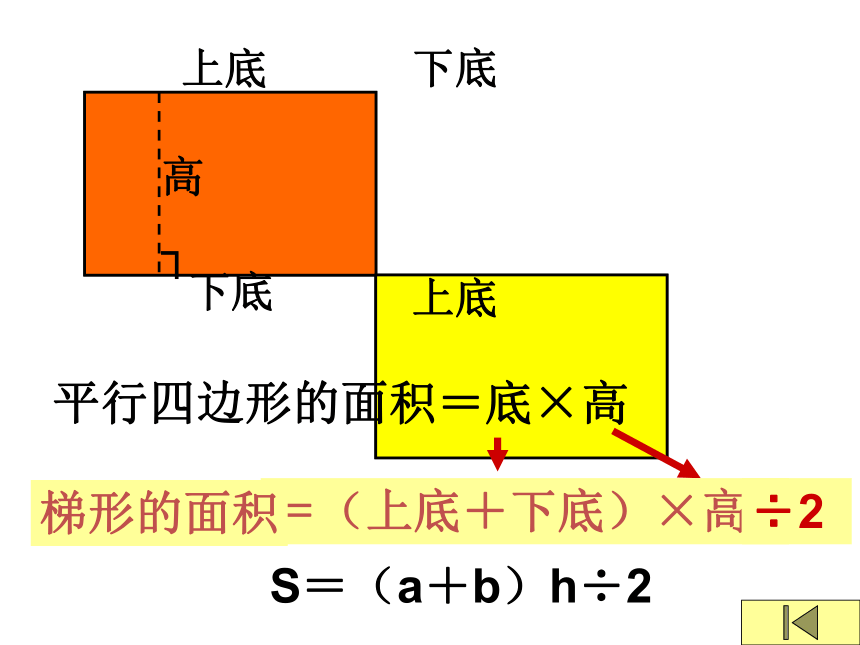
上底
下底
上底
下底
平行四边形的面积=底×高
=(上底+下底)×高
梯形的面积
S=(a+b)h÷2
÷2
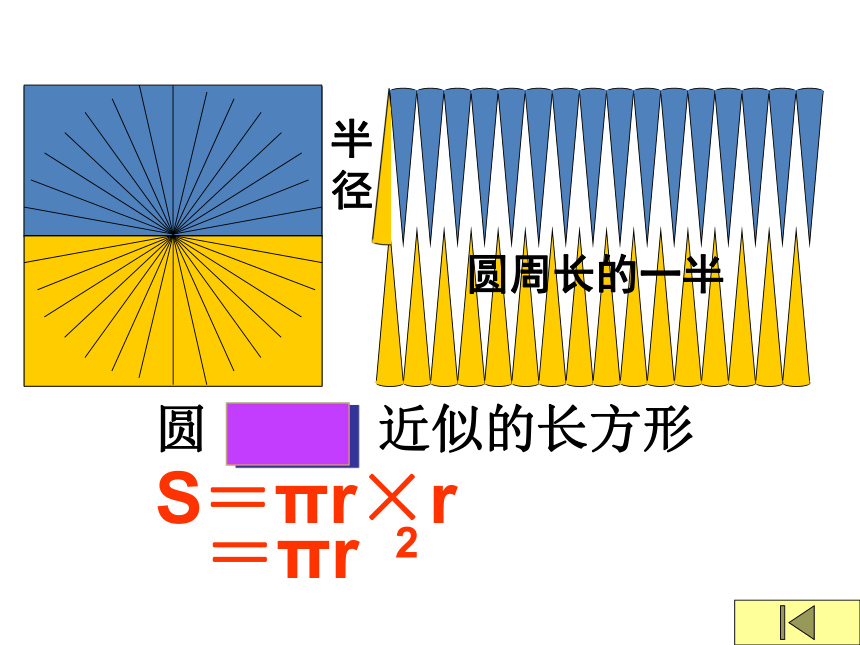
半径
圆周长的一半
圆
近似的长方形
S=πr×r
=πr
2
小组合作,用你喜欢的方法,根据这些平面图形面积推导之间的联系,画一画它们的关系图。
动一动,理一理:
a
a
a
a
a
b
b
h
h
h
S=
S=
S=
S=
S=
S=
b
平面图形面积
知识网络图
axb
a2
axh
axh÷2
(a+b)xh÷2
兀r2
1
2
3
小红的房间长4米,高3.2米,她爸爸准备把一面墙刷上彩漆,这面墙上窗户的面积是2.8平方米。算一算,小红爸爸至少需要买多少千克彩漆?(每平方米大约用彩漆0.4千克)。
1.你能计算出这个图形
中绿色部分的面积吗?
20厘米
20厘米
巩固提升
(只列式不计算)
20
20
计算下图中阴影部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
从前,有一个老人。他有三个儿子。一天,他把他们叫到跟前说:“孩子们,我已经老了。我没有多少家产留给你们,只有这个园子,就分给你们吧。”说着,老人拿出三根同样长的绳子,“你们每人拿一根绳子到园子里去圈地,谁圈到多大一块地,这块地就属于谁的谁
”
小故事
。你们圈剩下来的地就还留给我种吧!
6m
10m
如果你是老人的儿子,你会圈成什么样的图形呢?为什么?
实践探究
你能提出什么问题?
结
小
1.这本节课上,你学到了什么?
2.你有什么想要对老师说的?
谢谢同学们的合作,下课!
面积的概念很早就形成了。在古代埃及,尼罗河每年泛滥一次,洪水给两岸带来了肥沃的淤泥,但也抹掉了田地之间的界限标志。水退了,人们要重新划出田地的界限,就必须丈量和计算田地,于是逐渐有了面积的概念。在数学上是这样来研究面积问题的:首先规定边长为1的正方形的面积为1,并将其作为不证自明的公理。
面积的起源
平面图形的面积
1
20
8
4
3
3
2
1
1
S=ab
S=a
2
S=ah
S=ah÷2
S=(a+b)h÷2
s=πr
2
5分米
3分米
1分米
1分米
面积是1平方分米
5×3=15(平方分米)
长方形的面积=长×宽
S=ab
3分米
3分米
1分米
1分米
面积是1平方分米
3×3=9(平方分米)
正方形的面积=边长×边长
S=a
2
底
高
(长)
长方形的面积=长×宽
平行四边形的面积=底×高
S=ah
┐
高(宽)
底
┐
高
平行四边形的面积=底×高
三角形的面积=底×高÷2
S=ah÷2
高
┐
上底
下底
上底
下底
平行四边形的面积=底×高
=(上底+下底)×高
梯形的面积
S=(a+b)h÷2
÷2
半径
圆周长的一半
圆
近似的长方形
S=πr×r
=πr
2
小组合作,用你喜欢的方法,根据这些平面图形面积推导之间的联系,画一画它们的关系图。
动一动,理一理:
a
a
a
a
a
b
b
h
h
h
S=
S=
S=
S=
S=
S=
b
平面图形面积
知识网络图
axb
a2
axh
axh÷2
(a+b)xh÷2
兀r2
1
2
3
小红的房间长4米,高3.2米,她爸爸准备把一面墙刷上彩漆,这面墙上窗户的面积是2.8平方米。算一算,小红爸爸至少需要买多少千克彩漆?(每平方米大约用彩漆0.4千克)。
1.你能计算出这个图形
中绿色部分的面积吗?
20厘米
20厘米
巩固提升
(只列式不计算)
20
20
计算下图中阴影部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
3
4
2.求红色部分的面积
从前,有一个老人。他有三个儿子。一天,他把他们叫到跟前说:“孩子们,我已经老了。我没有多少家产留给你们,只有这个园子,就分给你们吧。”说着,老人拿出三根同样长的绳子,“你们每人拿一根绳子到园子里去圈地,谁圈到多大一块地,这块地就属于谁的谁
”
小故事
。你们圈剩下来的地就还留给我种吧!
6m
10m
如果你是老人的儿子,你会圈成什么样的图形呢?为什么?
实践探究
你能提出什么问题?
结
小
1.这本节课上,你学到了什么?
2.你有什么想要对老师说的?
谢谢同学们的合作,下课!
面积的概念很早就形成了。在古代埃及,尼罗河每年泛滥一次,洪水给两岸带来了肥沃的淤泥,但也抹掉了田地之间的界限标志。水退了,人们要重新划出田地的界限,就必须丈量和计算田地,于是逐渐有了面积的概念。在数学上是这样来研究面积问题的:首先规定边长为1的正方形的面积为1,并将其作为不证自明的公理。
面积的起源
