2020-2021学年八年级数学北师大版下册 第一章三角形的证明周末培优训练题(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册 第一章三角形的证明周末培优训练题(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 328.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 00:00:00 | ||
图片预览




文档简介
北师大版八年级数学下册 第一章《三角形的证明》
周末培优训练题
1.如图1,△ABC中,∠ABC=∠BAC,D是BC延长线上一动点,连接AD,AE平分∠CAD交CD于点E,过点E作EH⊥AB,垂足为点H.直线EH与直线AC相交于点F.设∠AEH=α,∠ADC=β.
(1)求证:∠EFC=∠FEC;
(2)①若∠B=30°,∠CAD=50°,则α= ,β= ;
②试探究α与β的关系,并说明理由;
(3)若将“D是BC延长线上一动点”改为“D是CB延长线上一动点”,其它条件不变,请在图2中补全图形,并直接写出α与β的关系.
2.如图,AD是△ABC的高,BE是△ABC的角平分线,F是AB中点,∠ABC=50°,∠CAD=60°.
(1)求∠AEB的度数;
(2)若△BCF与△ACF的周长差为3,AB=5,AC=8,求△ABC的周长.
3.在△ABC中,∠B=∠C,点D在BC上,点E在AC上,连接DE且∠ADE=∠AED.
{计算发现}
(1)若∠B=70°,∠ADE=80°,则∠BAD= ,∠CDE= .
{猜想验证}
(2)当点D在BC(点B,C除外)边上运动时(如图1),且点E在AC边上,猜想∠BAD与∠CDE的数量关系式,并证明你的猜想.
{拓展思考}
(3)①当点D在BC(点B,C除外)边上运动时(如图2),且点E在AC边上,若∠BAD=25°,则∠CDE= .
②当点D在BC(点B,C除外)边上运动时(如图2),且点E在AC边所在的直线上,若∠BAD=25°,则∠CDE= .
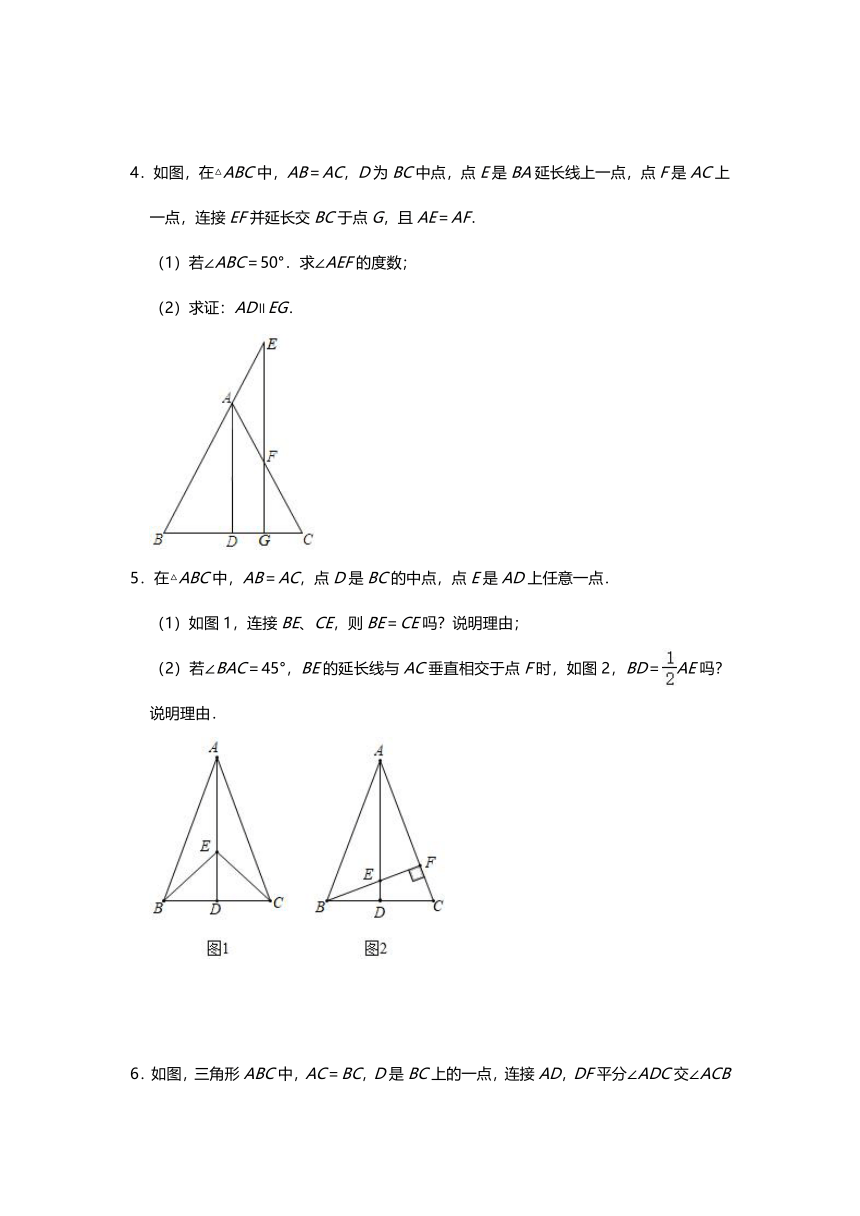
4.如图,在△ABC中,AB=AC,D为BC中点,点E是BA延长线上一点,点F是AC上一点,连接EF并延长交BC于点G,且AE=AF.
(1)若∠ABC=50°.求∠AEF的度数;
(2)求证:AD∥EG.
5.在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,则BE=CE吗?说明理由;
(2)若∠BAC=45°,BE的延长线与AC垂直相交于点F时,如图2,BD=AE吗?说明理由.
6.如图,三角形ABC中,AC=BC,D是BC上的一点,连接AD,DF平分∠ADC交∠ACB的外角∠ACE的平分线于F.
(1)求证:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度数.
7.如图,点O是△ABC边AC上的一个动点,过O点作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长.
8.如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连结CD,DE,已知∠EDB=∠ACD.
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB,BD=2时,求EB的长.
9.如图,已知∠1与∠2互为补角,且∠3=∠B,
(1)求证:EF∥BC;
(2)若AC=BC,CE平分∠ACB,求证:AF=CF.
10.在△ABC中,∠BAC=α,点D,点E在BC上,连接AD,AE.
(1)如图,若α=120°,BA=BE,CA=CD,求∠DAE的度数;
(2)若DA=DB,EA=EC,直接写出∠DAE= (用α的式子表示).
11.如图,在四边形ABCD中,AB∥CD,∠ABC的平分线交CD的延长线于点E,F是BE的中点,连接CF并延长交AD于点G.
(1)求证:CG平分∠BCD.
(2)若∠ADE=110°,∠ABC=52°,求∠CGD的度数.
12.如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A出发以1cm/s的速度向点C运动,同时点E从点C出发以2cm/s的速度向点B运动,运动的时间为t秒,解决以下问题:
(1)当t为何值时,△DEC为等边三角形;
(2)当t为何值时,△DEC为直角三角形.
13.在△ABC和△DCE中,CA=CB,CD=CE,∠CAB=∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点O:
①求证:BE=AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N,求证:N是BD的中点.
14.如图,△ABC是等边三角形,D、E、F分别是AB、BC、AC上一点,且∠DEF=60°.
(1)若∠1=50°,求∠2;
(2)连接DF,若DF∥BC,求证:∠1=∠3.
15.在等边△ABC中,
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.
16.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1)EF⊥AB;
(2)△ACF为等腰三角形.
17.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
参考答案
1.(1)证明:如图1中,
∵∠B=∠CAB,
∵EH⊥AB,
∴∠AHF=∠EHB=90°,
∴∠B+∠BEH=90°,∠CAB+∠AFH=90°,
∴∠BEH=∠AFH,
∵∠AFH=∠EFC,
∴∠EFC=∠FEC.
(2)①∵∠B=∠CAB=30°,
∴∠ACD=∠B+∠CAB=60°,
∵∠CAD=50°,
∴β=∠ADC=180°﹣50°﹣60°=70°,
∵EA平分∠DAC,
∴∠EAC=∠DAC=25°,
∴∠EAH=∠EAC+∠CAB=55°,
∵∠AHE=90°,
∴α=∠AEH=90°﹣55°=35°.
故答案为35°,70°.
②如图1中,设∠DAE=∠CAE=x,∠B=∠CAB=y.
∴β=∠ADC=180°﹣2(x+y),
∵∠AHE=90°,
∴α=∠AEH=90°﹣(x+y),
∴β=2α.
(3)图形如图所示:结论:α+=90°.
理由:设∠CBA=∠CAB=x,∠EAH=y.
∵AE平分∠CAD,
∴∠CAE=∠DAE=x﹣y,
∴∠DAB=x﹣y﹣y=x﹣2y,
∵∠CBA=∠ADC+∠BAD,
∴x=x﹣2y+β,
∴y=,
∵EH⊥AB,
∴∠AHE=90°,
∴∠AEH+∠EAH=90°,
∴α+=90°.
2.解:(1)∵AD是△ABC的高,
∴∠ADC=90°,
∵∠CAD=60°,
∴∠ACD=90°﹣60°=30°,
∵∠ABC=50°,BE是△ABC的角平分线,
∴∠CBE=ABC=25°,
∴∠AEB=∠CBE+∠ACB=25°+30°=55°;
(2)∵△BCF的周长=BC+BF+CF,△ACF的周长=AC+AF+CF,
∴△BCF的周长﹣△ACF的周长=BC+BF+CF﹣(AC+AF+CF)=3,
∵F是AB中点,
∴AF=BF,
∴BC﹣AC=3,
∵AC=8,
∴BC=11,
∴△ABC的周长=AB+BC+AC=5+11+8=24.
3.解:(1)∵∠B=∠C,∠ADE=∠AED,∠B=70°,∠ADE=80°,
∴∠C=70°,∠AED=80°,
∴∠CDE=∠AED﹣∠C=10°,
∠DAE=180°﹣∠ADE﹣∠AED=20°,
∴∠BAD=180°﹣∠B﹣∠C﹣∠DAE=20°,
故答案为:20°;10°;
(2)∠BAD=2∠CDE.
理由如下:
设∠B=x,∠ADE=y,
∵∠B=∠C,
∴∠C=x,
∵∠AED=∠ADE,
∴∠AED=y,
∴∠CDE=∠AED﹣∠C=y﹣x,
∠DAE=180°﹣∠ADE﹣∠AED=180°﹣2y,
∴∠BAD=180°﹣∠B﹣∠C﹣∠DAE=180°﹣x﹣x﹣(180°﹣2y)=2(y﹣x),
∴∠BAD=2∠CDE;
(3)①由(2)知,∠BAD=2∠CDE,
∴∠CDE=∠BAD=,
故答案为:12.5°;
②当E点在AC的延长线上时,AD<AC<AE,此时∠ADE≠∠AED,故点E不可能在AC的延长线上,
分两种情况:
当点E在线段AC上时,与①相同,∠CDE=12.5°;
当点E在CA的延长线上时,如图2,在AC边上截取AE′=AE,连接DE′,∵∠ADE=∠AED,
∴AE=AD=AE′,
∴∠ADE=∠AE′D,
由①知,∠CDE′=12.5°,
∴∠ADE+∠ADE′=∠AED+∠AE′D,
∵∠ADE+∠ADE′+∠AED+∠AE′D=180°,
∴∠ADE+∠ADE′=∠AED+∠AE′D=90°,
∴∠CDE=90°+12.5°=102.5°.
故答案为:12.5°或102.5°.
4.解:(1)∵AB=AC,
∴∠ABC=∠C=50°,
∴∠BAC=180°﹣50°﹣50°=80°,
D为BC中点,
∴AD⊥BC,AD平分∠BAC,
∴∠BAD=∠CAD=BAC=×80°=40°,
∵AE=AF,
∴∠E=∠AFE,
∵∠BAC=∠BAD+∠CAD=∠E+∠AFE,
∴∠AEF=∠BAD=40°;
(2)证明:由(1)得∠AEF=∠BAD,
∴AD∥EG.
5.解:(1)成立.
理由:∵AB=AC,D是BC的中点,
∴∠BAE=∠CAE.
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)成立.
理由:∵∠BAC=45°,BF⊥AF.
∴△ABF为等腰直角三角形
∴AF=BF,
由(1)知AD⊥BC,
∴∠EAF=∠CBF
在△AEF和△BCF中,,
∴△AEF≌△BCF(ASA),
∴AE=BC,
∵BD=BC,
∴BD=AE.
6.(1)证明:∵AC=BC,
∴∠ABC=∠CAB,
∴∠ACE=∠ABC+∠CAB=2∠ABC
∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE
∴2∠ABC=2∠FCE,
∴∠ABC=∠FCE,
∴CF∥AB;
(2)∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE=∠ADC+∠DAC
∵DF平分∠ADC,
∴∠ADC=2∠FDC;
∴2∠FCE=∠ADC+∠DAC=2∠FDC+∠DAC,
∴2∠FCE﹣2∠FDC=∠DAC
∵∠DFC=∠FCE﹣∠FDC
∴2∠DFC=2∠FCE﹣2∠FDC=∠DAC=40°
∴∠DFC=20°.
7.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF==10,
∴OC=EF=5.
8.(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵∠E+∠EDB=∠ABC=60°,∠ACD+∠DCB=60°,∠EDB=∠ACD,
∴∠E=∠DCE,
∴DE=DC,
∴△DEC是等腰三角形;
(2)解:设∠EDB=α,则∠BDC=5α,
∴∠E=∠DCE=60°﹣α,
∴6α+60°﹣α+60°﹣α=180°,
∴α=15°,
∴∠E=∠DCE=45°,
∴∠EDC=90°,
过D作DH⊥CE于H,
∵BD=2,∠DBH=60°,
∴BH=BD=1,DH==,DH=EH=,
∴BE=EH﹣BH=﹣1.
9.(1)证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC.
(2)解:∵EF∥BC,
∴∠BCE=∠FEC,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠FEC=∠ACE.
∴FC=FE,
∵AC=BC,
∴∠A=∠B,
又∵∠B=∠AEF,
∴∠A=∠AEF,
∴AF=FE,
∴AF=CF.
10.解:(1)∵BE=BA,
∴∠BAE=∠BEA,
∴∠B=180°﹣2∠BAE,①
∵CD=CA,
∴∠CAD=∠CDA,
∴∠C=180°﹣2∠CAD,②
①+②得:∠B+∠C=360°﹣2(∠BAE+∠CAD)
∴180°﹣∠BAC=360°﹣2[(∠BAD+∠DAE)+(∠DAE+∠CAE)],
∴﹣∠BAC=180°﹣2[(∠BAD+∠DAE+∠CAE)+∠DAE],
∴﹣∠BAC=180°﹣2(∠BAC+∠DAE),
∴2∠DAE=180°﹣∠BAC.
∵∠BAC=120°,
∴2∠DAE=180°﹣120°=60°,
∴∠DAE=30°;
(2)∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=∠B+∠C,
又在△ABC中,∠B+∠C=180°﹣∠BAC=180°﹣α,
∴∠DAB+∠EAC=180°﹣α,
∵∠DAB+∠DAE+∠CAE=α,
∴∠DAE+180°﹣α=α,
∴∠DAE=2α﹣180°,
故答案为:2α﹣180°.
11.(1)证明:∵BE平分∠ABC,
∴.
∵AB∥CD,
∴∠ABF=∠E,
∴∠CBF=∠E,
∴BC=CE,
∴△BCE是等腰三角形.
∵F为BE的中点,
∴CF平分∠BCD,
即CG平分∠BCD.
(2)解:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵∠ABC=52°,
∴∠BCD=128°.
∵CG平分∠BCD,
∴.
∵∠ADE=110°,∠ADE=∠CGD+∠GCD,
∴∠CGD=46°.
12.解:(1)根据题意可得 AD=t,CD=6﹣t,CE=2t
∵,∠B=30°,AC=6cm
∴BC=2AC=12cm,
∵∠C=90°﹣∠B=30°=60°,△DEC为等边三角形,
∴CD=CE,
6﹣t=2t,
t=2,
∴当t为2时,△DEC为等边三角形;
(2)①当∠DEC为直角时,∠EDC=30°,
∴CE=,
2t=(6﹣t),
t=;
②当∠EDC为直角时,∠DEC=30°,
CD=CE,
6﹣t=?2t,
t=3.
∴当t为或3时,△DEC为直角三角形.
13.解:(1)①∵CA=CB,CD=CE,∠CAB=∠CED=α,
∴∠ACB=180°﹣2α,∠DCE=180°﹣2α,
∴∠ACB=∠DCE,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS),
∴BE=AD;
②∵△ACD≌△BCE,
∴∠CAD=∠CBE=α+∠BAO,
∵∠ABE=∠BOA+∠BAO,
∴∠CBE+α=∠BOA+∠BAO,
∴∠BAO+α+α=∠BOA+∠BAO,
∴∠BOA=2α;
(2)如图2,作BP⊥MN交MN的延长线于P,作DQ⊥MN于Q,
∵∠BCP+∠BCA=∠CAM+∠AMC,
∵∠BCA=∠AMC,
∴∠BCP=∠CAM,
在△CBP与△ACM中,,
∴△CBP≌△ACM(AAS),
∴MC=BP,
同理,CM=DQ,
∴DQ=BP,
在△BPN与△DQN中,,
∴△BPN≌△DQN(AAS),
∴BN=ND,
∴N是BD的中点.
14.解:(1)∵△ABC是等边三角形,
∴∠B=∠A=∠C=60°,
∵∠B+∠1+∠DEB=180°,
∠DEB+∠DEF+∠2=180°,
∵∠DEF=60°,
∴∠1+∠DEB=∠2+∠DEB,
∴∠2=∠1=50°;
(2)连接DF,
∵DF∥BC,
∴∠FDE=∠DEB,
∵∠B+∠1+∠DEB=180°,∠FDE+∠3+∠DEF=180°,
∵∠B=60°,∠DEF=60°,
∴∠1=∠3.
15.解:(1)∵△ABC为等边三角形
∴∠B=60°
∴∠APC=∠BAP+∠B=80°
∵AP=AQ
∴∠AQB=∠APC=80°,
(2)①补全图形如图所示,
②证明:过点A作AH⊥BC于点H,如图.
由△ABC为等边三角形,AP=AQ,
可得∠PAB=∠QAC,
∵点Q,M关于直线AC对称,
∴∠QAC=∠MAC,AQ=AM
∴∠MAC+∠PAC=∠PAB+∠PAC=60°,
∵AP=AM,
∴△APM为等边三角形
∴PA=PM.
16.证明:(1)∵AB=AC,∠BAC=36°,
∴∠ABC=72°,
又∵BD是∠ABC的平分线,
∴∠ABD=36°,
∴∠BAD=∠ABD,
∴AD=BD,
又∵E是AB的中点,
∴DE⊥AB,即FE⊥AB;
(2)∵FE⊥AB,AE=BE,
∴FE垂直平分AB,
∴AF=BF,
∴∠BAF=∠ABF,
又∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°,
又∵∠ACB=72°,
∴∠AFC=∠ACB﹣∠CAF=36°,
∴∠CAF=∠AFC=36°,
∴AC=CF,即△ACF为等腰三角形.
17.解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,
∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,
∠BDA逐渐变小;
故答案为:25°,115°,小;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
∴△ABD≌△DCE(AAS),
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
理由:∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,
∴∠DAC=∠AED,
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,
∴∠ADC=100°,
∵∠C=40°,
∴∠DAC=40°,
∴∠DAC=∠ADE,
∴△ADE的形状是等腰三角形.
周末培优训练题
1.如图1,△ABC中,∠ABC=∠BAC,D是BC延长线上一动点,连接AD,AE平分∠CAD交CD于点E,过点E作EH⊥AB,垂足为点H.直线EH与直线AC相交于点F.设∠AEH=α,∠ADC=β.
(1)求证:∠EFC=∠FEC;
(2)①若∠B=30°,∠CAD=50°,则α= ,β= ;
②试探究α与β的关系,并说明理由;
(3)若将“D是BC延长线上一动点”改为“D是CB延长线上一动点”,其它条件不变,请在图2中补全图形,并直接写出α与β的关系.
2.如图,AD是△ABC的高,BE是△ABC的角平分线,F是AB中点,∠ABC=50°,∠CAD=60°.
(1)求∠AEB的度数;
(2)若△BCF与△ACF的周长差为3,AB=5,AC=8,求△ABC的周长.
3.在△ABC中,∠B=∠C,点D在BC上,点E在AC上,连接DE且∠ADE=∠AED.
{计算发现}
(1)若∠B=70°,∠ADE=80°,则∠BAD= ,∠CDE= .
{猜想验证}
(2)当点D在BC(点B,C除外)边上运动时(如图1),且点E在AC边上,猜想∠BAD与∠CDE的数量关系式,并证明你的猜想.
{拓展思考}
(3)①当点D在BC(点B,C除外)边上运动时(如图2),且点E在AC边上,若∠BAD=25°,则∠CDE= .
②当点D在BC(点B,C除外)边上运动时(如图2),且点E在AC边所在的直线上,若∠BAD=25°,则∠CDE= .
4.如图,在△ABC中,AB=AC,D为BC中点,点E是BA延长线上一点,点F是AC上一点,连接EF并延长交BC于点G,且AE=AF.
(1)若∠ABC=50°.求∠AEF的度数;
(2)求证:AD∥EG.
5.在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,则BE=CE吗?说明理由;
(2)若∠BAC=45°,BE的延长线与AC垂直相交于点F时,如图2,BD=AE吗?说明理由.
6.如图,三角形ABC中,AC=BC,D是BC上的一点,连接AD,DF平分∠ADC交∠ACB的外角∠ACE的平分线于F.
(1)求证:CF∥AB;
(2)若∠DAC=40°,求∠DFC的度数.
7.如图,点O是△ABC边AC上的一个动点,过O点作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=8,CF=6,求OC的长.
8.如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连结CD,DE,已知∠EDB=∠ACD.
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB,BD=2时,求EB的长.
9.如图,已知∠1与∠2互为补角,且∠3=∠B,
(1)求证:EF∥BC;
(2)若AC=BC,CE平分∠ACB,求证:AF=CF.
10.在△ABC中,∠BAC=α,点D,点E在BC上,连接AD,AE.
(1)如图,若α=120°,BA=BE,CA=CD,求∠DAE的度数;
(2)若DA=DB,EA=EC,直接写出∠DAE= (用α的式子表示).
11.如图,在四边形ABCD中,AB∥CD,∠ABC的平分线交CD的延长线于点E,F是BE的中点,连接CF并延长交AD于点G.
(1)求证:CG平分∠BCD.
(2)若∠ADE=110°,∠ABC=52°,求∠CGD的度数.
12.如图,在△ABC中,∠A=90°,∠B=30°,AC=6cm,点D从点A出发以1cm/s的速度向点C运动,同时点E从点C出发以2cm/s的速度向点B运动,运动的时间为t秒,解决以下问题:
(1)当t为何值时,△DEC为等边三角形;
(2)当t为何值时,△DEC为直角三角形.
13.在△ABC和△DCE中,CA=CB,CD=CE,∠CAB=∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点O:
①求证:BE=AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N,求证:N是BD的中点.
14.如图,△ABC是等边三角形,D、E、F分别是AB、BC、AC上一点,且∠DEF=60°.
(1)若∠1=50°,求∠2;
(2)连接DF,若DF∥BC,求证:∠1=∠3.
15.在等边△ABC中,
(1)如图1,P,Q是BC边上两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②求证:PA=PM.
16.如图,在△ABC中,AB=AC,∠BAC=36°,BD是∠ABC的平分线,交AC于点D,E是AB的中点,连接ED并延长,交BC的延长线于点F,连接AF,求证:
(1)EF⊥AB;
(2)△ACF为等腰三角形.
17.如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
参考答案
1.(1)证明:如图1中,
∵∠B=∠CAB,
∵EH⊥AB,
∴∠AHF=∠EHB=90°,
∴∠B+∠BEH=90°,∠CAB+∠AFH=90°,
∴∠BEH=∠AFH,
∵∠AFH=∠EFC,
∴∠EFC=∠FEC.
(2)①∵∠B=∠CAB=30°,
∴∠ACD=∠B+∠CAB=60°,
∵∠CAD=50°,
∴β=∠ADC=180°﹣50°﹣60°=70°,
∵EA平分∠DAC,
∴∠EAC=∠DAC=25°,
∴∠EAH=∠EAC+∠CAB=55°,
∵∠AHE=90°,
∴α=∠AEH=90°﹣55°=35°.
故答案为35°,70°.
②如图1中,设∠DAE=∠CAE=x,∠B=∠CAB=y.
∴β=∠ADC=180°﹣2(x+y),
∵∠AHE=90°,
∴α=∠AEH=90°﹣(x+y),
∴β=2α.
(3)图形如图所示:结论:α+=90°.
理由:设∠CBA=∠CAB=x,∠EAH=y.
∵AE平分∠CAD,
∴∠CAE=∠DAE=x﹣y,
∴∠DAB=x﹣y﹣y=x﹣2y,
∵∠CBA=∠ADC+∠BAD,
∴x=x﹣2y+β,
∴y=,
∵EH⊥AB,
∴∠AHE=90°,
∴∠AEH+∠EAH=90°,
∴α+=90°.
2.解:(1)∵AD是△ABC的高,
∴∠ADC=90°,
∵∠CAD=60°,
∴∠ACD=90°﹣60°=30°,
∵∠ABC=50°,BE是△ABC的角平分线,
∴∠CBE=ABC=25°,
∴∠AEB=∠CBE+∠ACB=25°+30°=55°;
(2)∵△BCF的周长=BC+BF+CF,△ACF的周长=AC+AF+CF,
∴△BCF的周长﹣△ACF的周长=BC+BF+CF﹣(AC+AF+CF)=3,
∵F是AB中点,
∴AF=BF,
∴BC﹣AC=3,
∵AC=8,
∴BC=11,
∴△ABC的周长=AB+BC+AC=5+11+8=24.
3.解:(1)∵∠B=∠C,∠ADE=∠AED,∠B=70°,∠ADE=80°,
∴∠C=70°,∠AED=80°,
∴∠CDE=∠AED﹣∠C=10°,
∠DAE=180°﹣∠ADE﹣∠AED=20°,
∴∠BAD=180°﹣∠B﹣∠C﹣∠DAE=20°,
故答案为:20°;10°;
(2)∠BAD=2∠CDE.
理由如下:
设∠B=x,∠ADE=y,
∵∠B=∠C,
∴∠C=x,
∵∠AED=∠ADE,
∴∠AED=y,
∴∠CDE=∠AED﹣∠C=y﹣x,
∠DAE=180°﹣∠ADE﹣∠AED=180°﹣2y,
∴∠BAD=180°﹣∠B﹣∠C﹣∠DAE=180°﹣x﹣x﹣(180°﹣2y)=2(y﹣x),
∴∠BAD=2∠CDE;
(3)①由(2)知,∠BAD=2∠CDE,
∴∠CDE=∠BAD=,
故答案为:12.5°;
②当E点在AC的延长线上时,AD<AC<AE,此时∠ADE≠∠AED,故点E不可能在AC的延长线上,
分两种情况:
当点E在线段AC上时,与①相同,∠CDE=12.5°;
当点E在CA的延长线上时,如图2,在AC边上截取AE′=AE,连接DE′,∵∠ADE=∠AED,
∴AE=AD=AE′,
∴∠ADE=∠AE′D,
由①知,∠CDE′=12.5°,
∴∠ADE+∠ADE′=∠AED+∠AE′D,
∵∠ADE+∠ADE′+∠AED+∠AE′D=180°,
∴∠ADE+∠ADE′=∠AED+∠AE′D=90°,
∴∠CDE=90°+12.5°=102.5°.
故答案为:12.5°或102.5°.
4.解:(1)∵AB=AC,
∴∠ABC=∠C=50°,
∴∠BAC=180°﹣50°﹣50°=80°,
D为BC中点,
∴AD⊥BC,AD平分∠BAC,
∴∠BAD=∠CAD=BAC=×80°=40°,
∵AE=AF,
∴∠E=∠AFE,
∵∠BAC=∠BAD+∠CAD=∠E+∠AFE,
∴∠AEF=∠BAD=40°;
(2)证明:由(1)得∠AEF=∠BAD,
∴AD∥EG.
5.解:(1)成立.
理由:∵AB=AC,D是BC的中点,
∴∠BAE=∠CAE.
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)成立.
理由:∵∠BAC=45°,BF⊥AF.
∴△ABF为等腰直角三角形
∴AF=BF,
由(1)知AD⊥BC,
∴∠EAF=∠CBF
在△AEF和△BCF中,,
∴△AEF≌△BCF(ASA),
∴AE=BC,
∵BD=BC,
∴BD=AE.
6.(1)证明:∵AC=BC,
∴∠ABC=∠CAB,
∴∠ACE=∠ABC+∠CAB=2∠ABC
∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE
∴2∠ABC=2∠FCE,
∴∠ABC=∠FCE,
∴CF∥AB;
(2)∵CF是∠ACE的平分线,
∴∠ACE=2∠FCE=∠ADC+∠DAC
∵DF平分∠ADC,
∴∠ADC=2∠FDC;
∴2∠FCE=∠ADC+∠DAC=2∠FDC+∠DAC,
∴2∠FCE﹣2∠FDC=∠DAC
∵∠DFC=∠FCE﹣∠FDC
∴2∠DFC=2∠FCE﹣2∠FDC=∠DAC=40°
∴∠DFC=20°.
7.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=8,CF=6,
∴EF==10,
∴OC=EF=5.
8.(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°,
∵∠E+∠EDB=∠ABC=60°,∠ACD+∠DCB=60°,∠EDB=∠ACD,
∴∠E=∠DCE,
∴DE=DC,
∴△DEC是等腰三角形;
(2)解:设∠EDB=α,则∠BDC=5α,
∴∠E=∠DCE=60°﹣α,
∴6α+60°﹣α+60°﹣α=180°,
∴α=15°,
∴∠E=∠DCE=45°,
∴∠EDC=90°,
过D作DH⊥CE于H,
∵BD=2,∠DBH=60°,
∴BH=BD=1,DH==,DH=EH=,
∴BE=EH﹣BH=﹣1.
9.(1)证明:∵∠1+∠FDE=180°,∠1,∠2互为补角,
∴∠2=∠FDE,
∴DF∥AB,
∴∠3=∠AEF,
∵∠3=∠B,
∴∠B=∠AEF,
∴FE∥BC.
(2)解:∵EF∥BC,
∴∠BCE=∠FEC,
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠FEC=∠ACE.
∴FC=FE,
∵AC=BC,
∴∠A=∠B,
又∵∠B=∠AEF,
∴∠A=∠AEF,
∴AF=FE,
∴AF=CF.
10.解:(1)∵BE=BA,
∴∠BAE=∠BEA,
∴∠B=180°﹣2∠BAE,①
∵CD=CA,
∴∠CAD=∠CDA,
∴∠C=180°﹣2∠CAD,②
①+②得:∠B+∠C=360°﹣2(∠BAE+∠CAD)
∴180°﹣∠BAC=360°﹣2[(∠BAD+∠DAE)+(∠DAE+∠CAE)],
∴﹣∠BAC=180°﹣2[(∠BAD+∠DAE+∠CAE)+∠DAE],
∴﹣∠BAC=180°﹣2(∠BAC+∠DAE),
∴2∠DAE=180°﹣∠BAC.
∵∠BAC=120°,
∴2∠DAE=180°﹣120°=60°,
∴∠DAE=30°;
(2)∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=∠B+∠C,
又在△ABC中,∠B+∠C=180°﹣∠BAC=180°﹣α,
∴∠DAB+∠EAC=180°﹣α,
∵∠DAB+∠DAE+∠CAE=α,
∴∠DAE+180°﹣α=α,
∴∠DAE=2α﹣180°,
故答案为:2α﹣180°.
11.(1)证明:∵BE平分∠ABC,
∴.
∵AB∥CD,
∴∠ABF=∠E,
∴∠CBF=∠E,
∴BC=CE,
∴△BCE是等腰三角形.
∵F为BE的中点,
∴CF平分∠BCD,
即CG平分∠BCD.
(2)解:∵AB∥CD,
∴∠ABC+∠BCD=180°.
∵∠ABC=52°,
∴∠BCD=128°.
∵CG平分∠BCD,
∴.
∵∠ADE=110°,∠ADE=∠CGD+∠GCD,
∴∠CGD=46°.
12.解:(1)根据题意可得 AD=t,CD=6﹣t,CE=2t
∵,∠B=30°,AC=6cm
∴BC=2AC=12cm,
∵∠C=90°﹣∠B=30°=60°,△DEC为等边三角形,
∴CD=CE,
6﹣t=2t,
t=2,
∴当t为2时,△DEC为等边三角形;
(2)①当∠DEC为直角时,∠EDC=30°,
∴CE=,
2t=(6﹣t),
t=;
②当∠EDC为直角时,∠DEC=30°,
CD=CE,
6﹣t=?2t,
t=3.
∴当t为或3时,△DEC为直角三角形.
13.解:(1)①∵CA=CB,CD=CE,∠CAB=∠CED=α,
∴∠ACB=180°﹣2α,∠DCE=180°﹣2α,
∴∠ACB=∠DCE,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS),
∴BE=AD;
②∵△ACD≌△BCE,
∴∠CAD=∠CBE=α+∠BAO,
∵∠ABE=∠BOA+∠BAO,
∴∠CBE+α=∠BOA+∠BAO,
∴∠BAO+α+α=∠BOA+∠BAO,
∴∠BOA=2α;
(2)如图2,作BP⊥MN交MN的延长线于P,作DQ⊥MN于Q,
∵∠BCP+∠BCA=∠CAM+∠AMC,
∵∠BCA=∠AMC,
∴∠BCP=∠CAM,
在△CBP与△ACM中,,
∴△CBP≌△ACM(AAS),
∴MC=BP,
同理,CM=DQ,
∴DQ=BP,
在△BPN与△DQN中,,
∴△BPN≌△DQN(AAS),
∴BN=ND,
∴N是BD的中点.
14.解:(1)∵△ABC是等边三角形,
∴∠B=∠A=∠C=60°,
∵∠B+∠1+∠DEB=180°,
∠DEB+∠DEF+∠2=180°,
∵∠DEF=60°,
∴∠1+∠DEB=∠2+∠DEB,
∴∠2=∠1=50°;
(2)连接DF,
∵DF∥BC,
∴∠FDE=∠DEB,
∵∠B+∠1+∠DEB=180°,∠FDE+∠3+∠DEF=180°,
∵∠B=60°,∠DEF=60°,
∴∠1=∠3.
15.解:(1)∵△ABC为等边三角形
∴∠B=60°
∴∠APC=∠BAP+∠B=80°
∵AP=AQ
∴∠AQB=∠APC=80°,
(2)①补全图形如图所示,
②证明:过点A作AH⊥BC于点H,如图.
由△ABC为等边三角形,AP=AQ,
可得∠PAB=∠QAC,
∵点Q,M关于直线AC对称,
∴∠QAC=∠MAC,AQ=AM
∴∠MAC+∠PAC=∠PAB+∠PAC=60°,
∵AP=AM,
∴△APM为等边三角形
∴PA=PM.
16.证明:(1)∵AB=AC,∠BAC=36°,
∴∠ABC=72°,
又∵BD是∠ABC的平分线,
∴∠ABD=36°,
∴∠BAD=∠ABD,
∴AD=BD,
又∵E是AB的中点,
∴DE⊥AB,即FE⊥AB;
(2)∵FE⊥AB,AE=BE,
∴FE垂直平分AB,
∴AF=BF,
∴∠BAF=∠ABF,
又∵∠ABD=∠BAD,
∴∠FAD=∠FBD=36°,
又∵∠ACB=72°,
∴∠AFC=∠ACB﹣∠CAF=36°,
∴∠CAF=∠AFC=36°,
∴AC=CF,即△ACF为等腰三角形.
17.解:(1)∠EDC=180°﹣∠ADB﹣∠ADE=180°﹣115°﹣40°=25°,
∠DEC=180°﹣∠EDC﹣∠C=180°﹣40°﹣25°=115°,
∠BDA逐渐变小;
故答案为:25°,115°,小;
(2)当DC=2时,△ABD≌△DCE,
理由:∵∠C=40°,
∴∠DEC+∠EDC=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
又∵AB=DC=2,
∴△ABD≌△DCE(AAS),
(3)当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形,
理由:∵∠BDA=110°时,
∴∠ADC=70°,
∵∠C=40°,
∴∠DAC=70°,∠AED=∠C+∠EDC=30°+40°=70°,
∴∠DAC=∠AED,
∴△ADE的形状是等腰三角形;
∵当∠BDA的度数为80°时,
∴∠ADC=100°,
∵∠C=40°,
∴∠DAC=40°,
∴∠DAC=∠ADE,
∴△ADE的形状是等腰三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
