18.1.1 平行四边形的性质课件(18张)
文档属性
| 名称 | 18.1.1 平行四边形的性质课件(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 905.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-19 13:16:42 | ||
图片预览




文档简介
18.1.1 平行四边形的性质
平行四边形的边、角特征
学习目标
1.理解平行四边形的定义及有关概念.
2. 掌握平行四边形的对边相等、对角相等的性质.(重点)
3. 能根据平行四边形的性质进行简单的计算和证明.(难点)
4.了解平行线间的距离的概念.
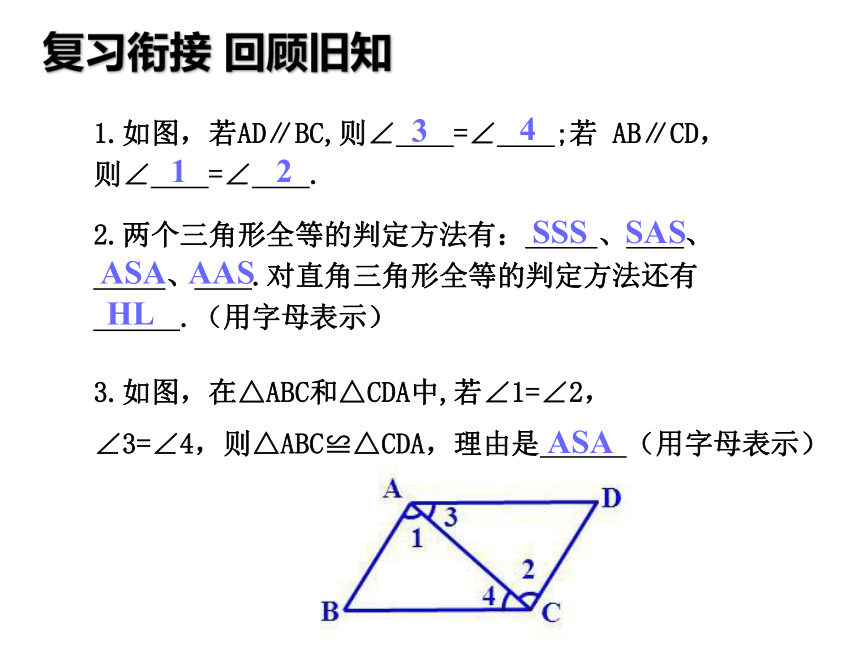
1.如图,若AD∥BC,则∠ =∠ ;若 AB∥CD, 则∠ =∠ .
2.两个三角形全等的判定方法有: 、 、
、 .对直角三角形全等的判定方法还有
.(用字母表示)
3.如图,在△ABC和△CDA中,若∠1=∠2,
∠3=∠4,则△ABC≌△CDA,理由是 (用字母表示)
1
2
3
4
HL
AAS
ASA
SSS
SAS
ASA
复习衔接 回顾旧知
问题发现 感受新知
问题:
下面的图片中,有你熟悉的哪些图形?如果有,是什么图形呢?
平行四边形的定义
问题1 用两个全等的三角形,能拼出怎样的四边形? 拼拼看.
合作探究 获取新知
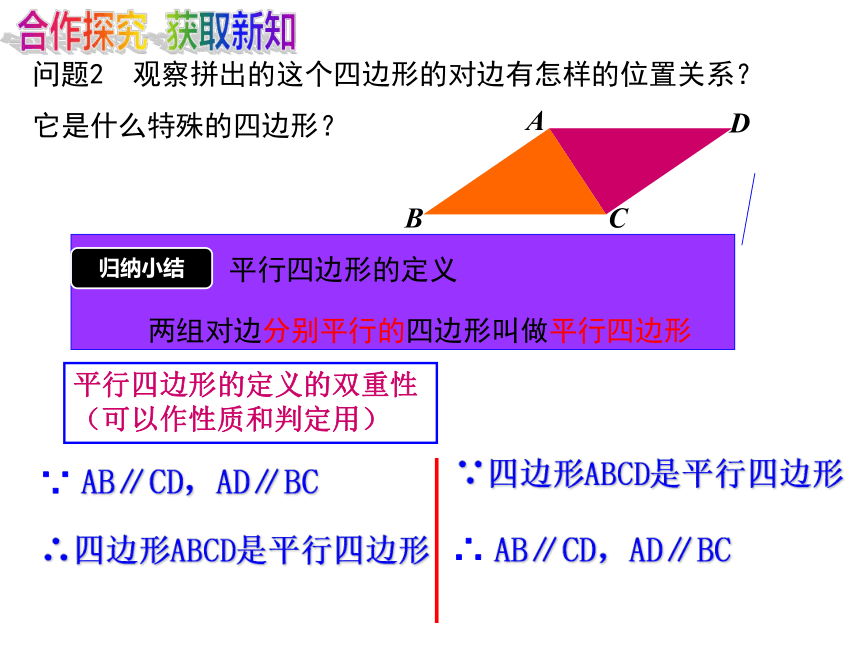
问题2 观察拼出的这个四边形的对边有怎样的位置关系?它是什么特殊的四边形?
A
B
C
D
合作探究 获取新知
归纳小结
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形
∵ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
∴ AB∥CD,AD∥BC
平行四边形的定义的双重性
(可以作性质和判定用)
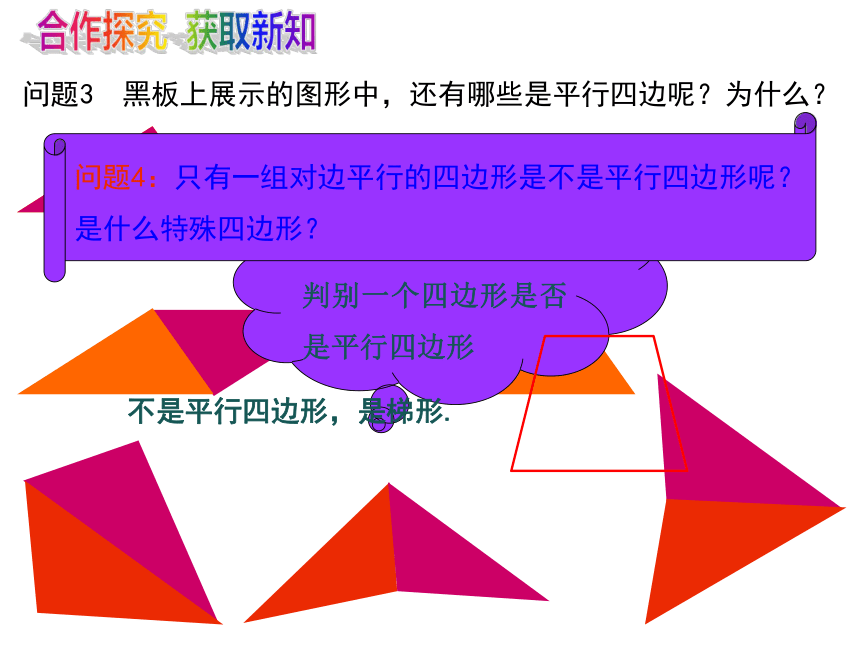
问题3 黑板上展示的图形中,还有哪些是平行四边呢?为什么?
合作探究 获取新知
说明:定义可以用来判别一个四边形是否是平行四边形
问题4:只有一组对边平行的四边形是不是平行四边形呢?
是什么特殊四边形?
不是平行四边形,是梯形.
1.平行四边形的表示方法.
如图:四边形ABCD是平行四边形记作: ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边, 相对的角称为 对角.
平行四边形相关概念
A
D
C
B
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
注意: 图形中字母的标识顺序应为顺时针方向或逆时针方向。
合作探究 获取新知
线段AC、BD就是 ABCD的两条对角线。
4. 平行四边形中,相邻的边、角分别简称为邻边、邻角.
如:邻边:AB与AD; BC与CD.
如:对角: ∠ABC与∠BCD; ∠BAD与∠ABC.
平行四边形的性质
问题5 研究等腰三角形的性质是从哪些方面考虑的?
边和角
边和角
追问:那么研究平行四边形首先可以从哪些方面考虑?
合作探究 获取新知
A
B
C
D
平行四边形的性质
合作探究 获取新知
平行四边形的性质
合作探究 获取新知
探究归纳
1、猜一猜:
(1)对边除了平行,是否还有其他关系?
(2)对角又会存在怎样的关系?
2、画一画
师?:上面仅仅是同学们的猜想和假设,现在我们一起来验证以上的结论,请同学们拿出方格纸,按照上面的提示画一画图。
平行四边形的性质
合作探究 获取新知
平行四边形的性质
3、量一量
请同学们在刚才所画的平行四边形中,量一量边和角,看看对边及对角有什么关系?
猜想结论:平行四边形的对边 ,对角 ,
邻角 。
互补
相等
相等
由上面知,△ABC≌△CDA ∴ ∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.
证明:如图,连接AC
∵AD∥BC,AB ∥ CD
∴∠1=∠2,∠3=∠4
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA
∴AD=CD,AB=CD,
∠B=∠D
1.同学们自己证明∠BAD=∠DCB
2.不添加辅助线,你能否
直接运用平行四边形的定义,
证明其对角相等?
说理验证
A
B
C
D
怎样证明平行四边形的对边相等和对角相等呢?
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
平行四边形的性质
归纳小结
A
B
C
D
合作探究 获取新知
例1 如图,在□ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,
则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,
则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
(1)平行四边形的对角相等;(2)平行四边形的
邻角互补;(3)平行四边形的一组邻边之和等于周长的一半,反之,周长=2倍邻边之和.
归纳
实战演练 运用新知
?
D
A
B
C
F
E
证明:
?
?
?
?
?
平行四边形为证明线段及角相等提供了一种新的
思路.
归纳
两条平行线间的距离
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(因为平行四边形的对边相等)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
合作探究 获取新知
1.在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A .45° B. 55° C. 65° D. 75°
A
A
B
C
M
D
2.在□ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A .3 B. 5 C. 2或3 D. 3或5
D
巩固新知 深化理解
3.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
10
4.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
巩固新知 深化理解
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等.
两条平行线间的距离相等
两组对角分别相等,邻角互补.
反思小结 提炼升华
1.通过今天的学习,获得了哪些数学知识和思想方法?
数学思想:转化思想、分类思想
2.通过今天的学习,你还有什么困难和疑惑呢?
平行四边形的边、角特征
学习目标
1.理解平行四边形的定义及有关概念.
2. 掌握平行四边形的对边相等、对角相等的性质.(重点)
3. 能根据平行四边形的性质进行简单的计算和证明.(难点)
4.了解平行线间的距离的概念.
1.如图,若AD∥BC,则∠ =∠ ;若 AB∥CD, 则∠ =∠ .
2.两个三角形全等的判定方法有: 、 、
、 .对直角三角形全等的判定方法还有
.(用字母表示)
3.如图,在△ABC和△CDA中,若∠1=∠2,
∠3=∠4,则△ABC≌△CDA,理由是 (用字母表示)
1
2
3
4
HL
AAS
ASA
SSS
SAS
ASA
复习衔接 回顾旧知
问题发现 感受新知
问题:
下面的图片中,有你熟悉的哪些图形?如果有,是什么图形呢?
平行四边形的定义
问题1 用两个全等的三角形,能拼出怎样的四边形? 拼拼看.
合作探究 获取新知
问题2 观察拼出的这个四边形的对边有怎样的位置关系?它是什么特殊的四边形?
A
B
C
D
合作探究 获取新知
归纳小结
平行四边形的定义
两组对边分别平行的四边形叫做平行四边形
∵ AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
∴ AB∥CD,AD∥BC
平行四边形的定义的双重性
(可以作性质和判定用)
问题3 黑板上展示的图形中,还有哪些是平行四边呢?为什么?
合作探究 获取新知
说明:定义可以用来判别一个四边形是否是平行四边形
问题4:只有一组对边平行的四边形是不是平行四边形呢?
是什么特殊四边形?
不是平行四边形,是梯形.
1.平行四边形的表示方法.
如图:四边形ABCD是平行四边形记作: ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边, 相对的角称为 对角.
平行四边形相关概念
A
D
C
B
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
注意: 图形中字母的标识顺序应为顺时针方向或逆时针方向。
合作探究 获取新知
线段AC、BD就是 ABCD的两条对角线。
4. 平行四边形中,相邻的边、角分别简称为邻边、邻角.
如:邻边:AB与AD; BC与CD.
如:对角: ∠ABC与∠BCD; ∠BAD与∠ABC.
平行四边形的性质
问题5 研究等腰三角形的性质是从哪些方面考虑的?
边和角
边和角
追问:那么研究平行四边形首先可以从哪些方面考虑?
合作探究 获取新知
A
B
C
D
平行四边形的性质
合作探究 获取新知
平行四边形的性质
合作探究 获取新知
探究归纳
1、猜一猜:
(1)对边除了平行,是否还有其他关系?
(2)对角又会存在怎样的关系?
2、画一画
师?:上面仅仅是同学们的猜想和假设,现在我们一起来验证以上的结论,请同学们拿出方格纸,按照上面的提示画一画图。
平行四边形的性质
合作探究 获取新知
平行四边形的性质
3、量一量
请同学们在刚才所画的平行四边形中,量一量边和角,看看对边及对角有什么关系?
猜想结论:平行四边形的对边 ,对角 ,
邻角 。
互补
相等
相等
由上面知,△ABC≌△CDA ∴ ∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.
证明:如图,连接AC
∵AD∥BC,AB ∥ CD
∴∠1=∠2,∠3=∠4
又AC是△ABC和△CDA的公共边,
∴ △ABC≌ △CDA
∴AD=CD,AB=CD,
∠B=∠D
1.同学们自己证明∠BAD=∠DCB
2.不添加辅助线,你能否
直接运用平行四边形的定义,
证明其对角相等?
说理验证
A
B
C
D
怎样证明平行四边形的对边相等和对角相等呢?
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
平行四边形的性质
归纳小结
A
B
C
D
合作探究 获取新知
例1 如图,在□ABCD中
(1)若∠A=130°,则∠B=______ ,∠C=______ , ∠D=______。
(2)若∠A+ ∠C= 200°,则∠A=______ ,∠B=______.
(3)若∠A:∠B= 5:4,
则∠C=______ ,∠D=______.
(4)若AB=3,BC=5,
则它的周长= ______.
C
D
A
B
50°
130°
50°
100°
80°
100°
80°
16
(1)平行四边形的对角相等;(2)平行四边形的
邻角互补;(3)平行四边形的一组邻边之和等于周长的一半,反之,周长=2倍邻边之和.
归纳
实战演练 运用新知
?
D
A
B
C
F
E
证明:
?
?
?
?
?
平行四边形为证明线段及角相等提供了一种新的
思路.
归纳
两条平行线间的距离
H
A
B
C
D
G
若a // b,作 AD // GH // BC,分别交 b于D、H、C,交 a于A、G、B.
两条平行线间的距离
则 GH=AD=BC.
两条平行线之间的平行线段相等
则 DA HG CB.
(因为平行四边形的对边相等)
若a // b,DA、GH、CB垂直于 a,交a于A、G、B,交 b于D、H、C.
b
a
A
B
C
D
a
b
H
G
点到直线的距离
=
=
相等
合作探究 获取新知
1.在□ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A .45° B. 55° C. 65° D. 75°
A
A
B
C
M
D
2.在□ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,则AB的长为( )
A .3 B. 5 C. 2或3 D. 3或5
D
巩固新知 深化理解
3.如图,直线AE//BD,点C在BD上,若AE=5,BD=8,△ABD的面积为16,则△ACE的面积为 .
A
B
C
D
E
10
4.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
解:∵AE//BC,AB//CF,
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°,
AD=BC=60cm.
∴ED=AD-AE=80-60=20cm.
答:DE的长度是20cm, ∠D的度数是60°.
巩固新知 深化理解
平行
四边形
定义
两组对边分别平行的四边形
性质
两组对边分别平行,相等.
两条平行线间的距离相等
两组对角分别相等,邻角互补.
反思小结 提炼升华
1.通过今天的学习,获得了哪些数学知识和思想方法?
数学思想:转化思想、分类思想
2.通过今天的学习,你还有什么困难和疑惑呢?
