5.1.2 垂线 课件 (53张)
图片预览







文档简介
(共53张PPT)
第五章
5.1.2
垂线
人教版数学七年级下册
如图所示是北京天安门
广场庄严隆重的升国旗仪式,
是亿万中国人民特别关注的
活动.众所周知,1949年10
月1日,毛泽东主席在天安
门城楼上用洪亮的声音向全
世界宣告中华人民共和国诞
生,亲手升起了第一面五星
红旗.
导入新知
天安门广场的升国旗仪式一招一式欣赏性极强,
人们概括有“五绝”.一绝:升旗;二绝:护旗;三绝:
敬礼;四绝:礼毕;五绝:收旗.其中的每招每式都有
极其严格的要求.每一次,当擎旗手以优美的动作,在
国歌奏响第一个音符时,将国旗展开抛出,到国歌的
最后一个音符终止,都是2分07秒,国旗也准时到达30
米高的旗杆顶端,做到了分秒不差.可是,你看着旗杆
与地面,会想到旗杆与地面有怎样的位置关系呢?
1.认识生活中的垂直现象,理解垂直定义,并能用符号表示.掌握垂线的性质,会过一点作已知直线的垂线.
2.经历垂线画法,垂线的性质以及点到直线的距离的探索过程,尝试从不同角度寻求垂线的画法,用不同方法得到垂线的性质.
学习目标
1
知识点
垂直的定义
观察思考
当转动一木条的位置时,什么也随着发生了变化?
合作探究
a
b
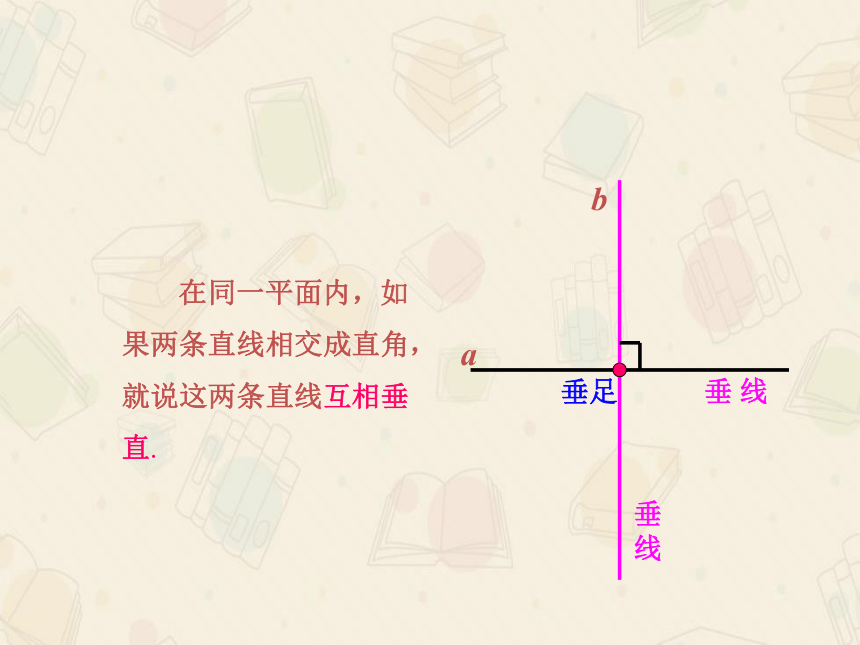
在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直.
垂足
垂
线
垂
线
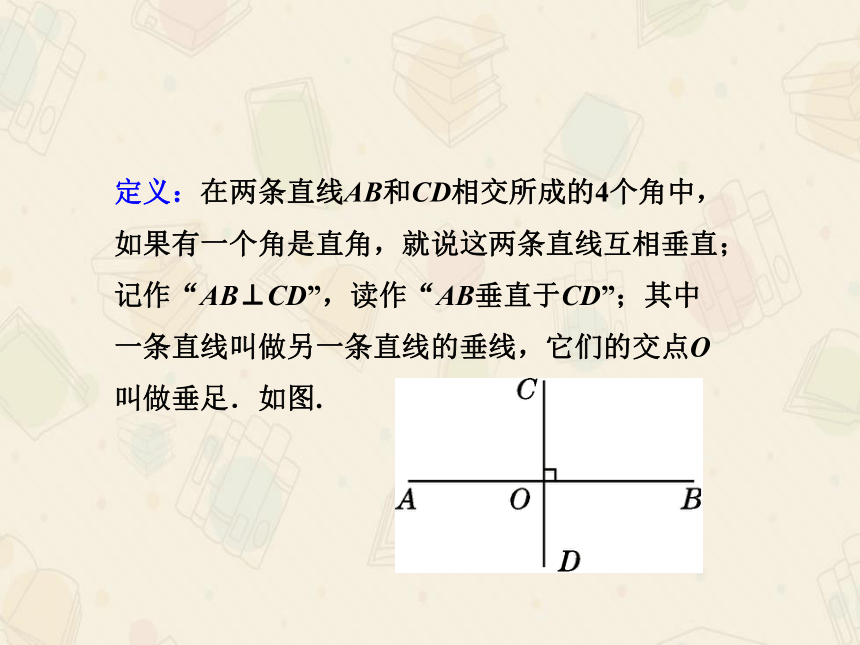
定义:在两条直线AB和CD相交所成的4个角中,
如果有一个角是直角,就说这两条直线互相垂直;
记作“AB⊥CD”,读作“AB垂直于CD”;其中
一条直线叫做另一条直线的垂线,它们的交点O
叫做垂足.如图.
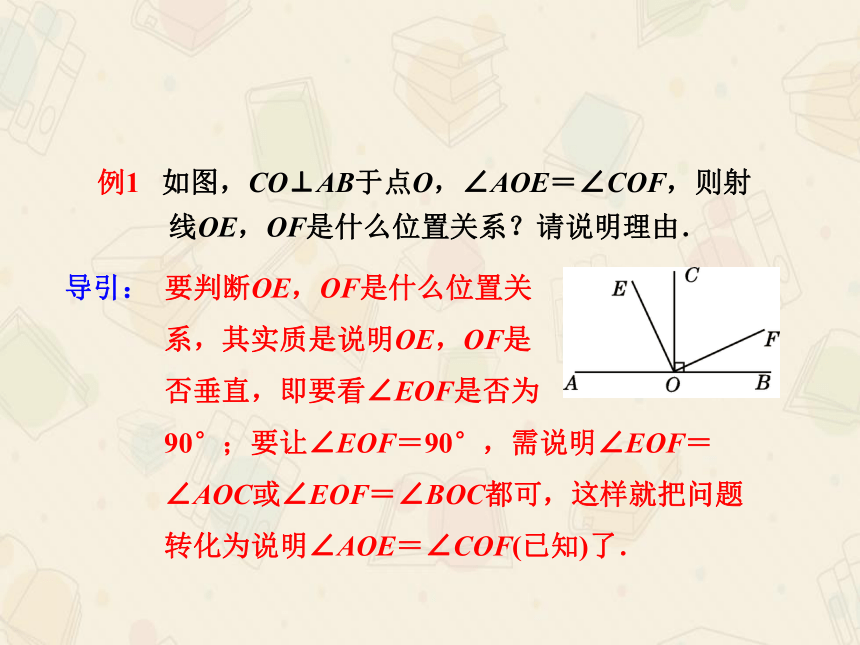
导引:
要判断OE,OF是什么位置关
系,其实质是说明OE,OF是
否垂直,即要看∠EOF是否为
90°;要让∠EOF=90°,需说明∠EOF=
∠AOC或∠EOF=∠BOC都可,这样就把问题
转化为说明∠AOE=∠COF(已知)了.
例1
如图,CO⊥AB于点O,∠AOE=∠COF,则射
线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE与OF互相垂直(垂直定义).
判断两直线(线段、射线所在直线)互相垂直,主要
依据是垂直定义,只要说明两条相交直线所构成的四
个角中有一个角是直角即可.
新知小结
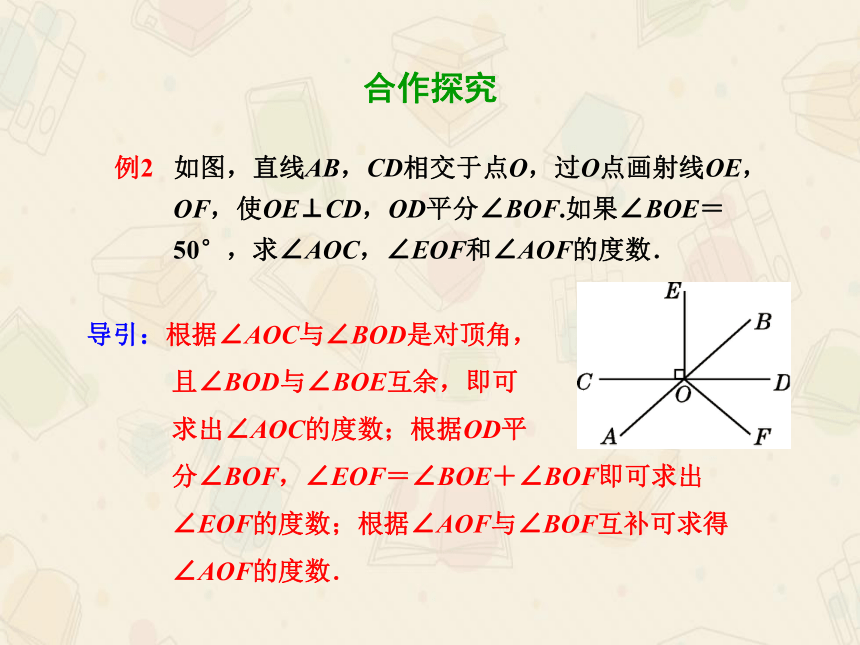
导引:根据∠AOC与∠BOD是对顶角,
且∠BOD与∠BOE互余,即可
求出∠AOC的度数;根据OD平
分∠BOF,∠EOF=∠BOE+∠BOF即可求出
∠EOF的度数;根据∠AOF与∠BOF互补可求得
∠AOF的度数.
例2
如图,直线AB,CD相交于点O,过O点画射线OE,
OF,使OE⊥CD,OD平分∠BOF.如果∠BOE=
50°,求∠AOC,∠EOF和∠AOF的度数.
合作探究
解:因为OE⊥CD,所以∠DOE=90°(垂直定义).
因为∠BOE=50°,
所以∠AOC=∠BOD=∠DOE-∠BOE=
90°-50°=40°.
因为OD平分∠BOF,
所以∠BOF=2∠BOD=80°.
所以∠EOF=∠BOF+∠BOE=80°+50°=130°,
∠AOF=∠AOB-∠BOF=180°-80°=100°.
1
当两条直线相交所成的四个角都相等时,这两条直线有什么位置关系?为什么?
当两条直线相交,所成的四个角都相等时,这两条直线互相垂直.理由:设所成的四个角中有一个角的度数为m°,则其余三个角的度数分别为180°-m°,m°,180°-m°,由题意知,m°=180°-m°,得m°=90°,所以180°-m°=90°,所以这两条直线互相垂直.
解:
巩固新知
如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35°
B.45°
C.55°
D.65°
2
C
【中考·德宏州】如图,三条直线相交于点O,
若CO⊥AB,∠1=56°,则∠2等于( )
A.30°
B.34°
C.45°
D.56°
3
B
如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36°
B.54°
C.55°
D.44°
4
B
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为( )
A.35°
B.45°
C.55°
D.65°
5
C
已知在同一平面内:
①两条直线相交成直角;
②两条直线互相垂直;
③一条直线是另一条直线的垂线.
那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A.0个
B.1个
C.2个
D.3个
6
D
2
知识点
垂线的画法
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线.
如果作线段互相垂直或作射线的垂
线,实际上是作线段所在的直线互相垂直,或作射线
所在的直线的垂线,因为射线和线段都是直线的一部
分.在垂线的画法中,有时需延长线段,垂足在延长
线上,并记上直角符号“﹁”.
合作探究
注意:画垂线也可用以下两种方法:
(1)利用量角器画;(2)用折叠法画.
例3
如图,M是三角形ABC中BC边上的任意一点,请
你按照下列要求画图:
(1)过M点画直线AB的垂线m;
(2)过M点画直线BC的垂线n;
(3)过M点画直线AC的垂线p.
导引:观察图形不难看出,(1)(3)属于过直线外一点画
已知直线的垂线,(2)属于过直线上一点画已知
直线的垂线,所以按照“一靠、二过、三画”
的方法画图即可.
解:画出的直线m,n,p如上页图.
过已知点画已知直线的垂线,实际上就是过已知
点画一条直线,使所画直线与已知直线相交所成的角
是90°.
新知小结
过一条线段外一点,作这条线段的垂线,垂足
在( )
A.这条线段上
B.这条线段的端点处
C.这条线段的延长线上
D.以上都有可能
1
D
巩固新知
3
知识点
垂线的性质
探究
如图.
(1)用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
(2)经过直线l上一点A画l的垂线,这样的垂线能画出几条?
(3)经过直线l外一点B画l的垂线,这样的垂线能画出几条?
合作探究
经过一点(已知直线上或直线外),能画出已知直
线的一条垂线,并且只
能画出一条垂线.即
在同一平面内,过一点有且只有一条直线与已知
直线垂直.
新知小结
在平面内,不是在空间内,这是需要注意的条件:
其中,一点可以是直线上一点也可以是直线外一点;
“有且只有”中的“有”是指能画出一条已知直线的
垂线,即存在性,“只有”是指只能画一条,即唯
一性.
例4〈厦门〉如图,已知直线AB,CB,l在同一平面内,
若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合
题意的图形可以是( )
C
合作探究
导引:根据题意可知,过点B有AB,CB都与直线l垂直,
由垂线的性质可知,在同一平面内,过一点有且
只有一条直线与已知直线垂直,所以A、B、C三
点在一条直线上.
利用直线的性质解答题目,要注意直线性质满足的条件:
1.
在平面内;
2.
过一点,点的位置可以在直线上也可以在直线外;
3.
相交所成的角必须是直角,以上三条缺一不可.
新知小结
在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
1
C
巩固新知
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只
有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已
知直线垂直
D.两点之间,线段最短
2
C
以下几个方面由学生自己总结:
①
垂线的定义及垂直的符号表示;
②
垂线的有关性质;
③
过一点作已知直线的垂线的方法.
1
知识小结
归纳新知
(1)在图①中,过AB外一点M作AB的垂线;
(2)在图②中,过点A,B分别作OB,OA的垂线.
2
易错小结
解:
(1)如图①所示.
(2)如图②所示.
本题易错之处在于误认为垂足一定落在线段或射线上.
易错点:误认为垂足一定要在线段或射线上而导致
错误.
互相垂直
AB⊥CD
∠AOC=∠BOC=∠BOD=∠AOD=90°
课后练习
B
C
B
D
用三角尺的一条直角边靠在已知直线上
使已知点落在另一条直角边上
过已知点画出与已知直线垂直的直线
C
有且只有
上
存在
唯一
D
B
【答案】A
再见
第五章
5.1.2
垂线
人教版数学七年级下册
如图所示是北京天安门
广场庄严隆重的升国旗仪式,
是亿万中国人民特别关注的
活动.众所周知,1949年10
月1日,毛泽东主席在天安
门城楼上用洪亮的声音向全
世界宣告中华人民共和国诞
生,亲手升起了第一面五星
红旗.
导入新知
天安门广场的升国旗仪式一招一式欣赏性极强,
人们概括有“五绝”.一绝:升旗;二绝:护旗;三绝:
敬礼;四绝:礼毕;五绝:收旗.其中的每招每式都有
极其严格的要求.每一次,当擎旗手以优美的动作,在
国歌奏响第一个音符时,将国旗展开抛出,到国歌的
最后一个音符终止,都是2分07秒,国旗也准时到达30
米高的旗杆顶端,做到了分秒不差.可是,你看着旗杆
与地面,会想到旗杆与地面有怎样的位置关系呢?
1.认识生活中的垂直现象,理解垂直定义,并能用符号表示.掌握垂线的性质,会过一点作已知直线的垂线.
2.经历垂线画法,垂线的性质以及点到直线的距离的探索过程,尝试从不同角度寻求垂线的画法,用不同方法得到垂线的性质.
学习目标
1
知识点
垂直的定义
观察思考
当转动一木条的位置时,什么也随着发生了变化?
合作探究
a
b
在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直.
垂足
垂
线
垂
线
定义:在两条直线AB和CD相交所成的4个角中,
如果有一个角是直角,就说这两条直线互相垂直;
记作“AB⊥CD”,读作“AB垂直于CD”;其中
一条直线叫做另一条直线的垂线,它们的交点O
叫做垂足.如图.
导引:
要判断OE,OF是什么位置关
系,其实质是说明OE,OF是
否垂直,即要看∠EOF是否为
90°;要让∠EOF=90°,需说明∠EOF=
∠AOC或∠EOF=∠BOC都可,这样就把问题
转化为说明∠AOE=∠COF(已知)了.
例1
如图,CO⊥AB于点O,∠AOE=∠COF,则射
线OE,OF是什么位置关系?请说明理由.
解:射线OE,OF互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE与OF互相垂直(垂直定义).
判断两直线(线段、射线所在直线)互相垂直,主要
依据是垂直定义,只要说明两条相交直线所构成的四
个角中有一个角是直角即可.
新知小结
导引:根据∠AOC与∠BOD是对顶角,
且∠BOD与∠BOE互余,即可
求出∠AOC的度数;根据OD平
分∠BOF,∠EOF=∠BOE+∠BOF即可求出
∠EOF的度数;根据∠AOF与∠BOF互补可求得
∠AOF的度数.
例2
如图,直线AB,CD相交于点O,过O点画射线OE,
OF,使OE⊥CD,OD平分∠BOF.如果∠BOE=
50°,求∠AOC,∠EOF和∠AOF的度数.
合作探究
解:因为OE⊥CD,所以∠DOE=90°(垂直定义).
因为∠BOE=50°,
所以∠AOC=∠BOD=∠DOE-∠BOE=
90°-50°=40°.
因为OD平分∠BOF,
所以∠BOF=2∠BOD=80°.
所以∠EOF=∠BOF+∠BOE=80°+50°=130°,
∠AOF=∠AOB-∠BOF=180°-80°=100°.
1
当两条直线相交所成的四个角都相等时,这两条直线有什么位置关系?为什么?
当两条直线相交,所成的四个角都相等时,这两条直线互相垂直.理由:设所成的四个角中有一个角的度数为m°,则其余三个角的度数分别为180°-m°,m°,180°-m°,由题意知,m°=180°-m°,得m°=90°,所以180°-m°=90°,所以这两条直线互相垂直.
解:
巩固新知
如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35°
B.45°
C.55°
D.65°
2
C
【中考·德宏州】如图,三条直线相交于点O,
若CO⊥AB,∠1=56°,则∠2等于( )
A.30°
B.34°
C.45°
D.56°
3
B
如图,点O在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB的大小为( )
A.36°
B.54°
C.55°
D.44°
4
B
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON的度数为( )
A.35°
B.45°
C.55°
D.65°
5
C
已知在同一平面内:
①两条直线相交成直角;
②两条直线互相垂直;
③一条直线是另一条直线的垂线.
那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A.0个
B.1个
C.2个
D.3个
6
D
2
知识点
垂线的画法
用三角尺画垂线的方法:
一贴,用三角尺的一条直角边贴住已知直线;
二靠,用三角尺的另一条直角边靠住已知点;
三画,画出垂线.
如果作线段互相垂直或作射线的垂
线,实际上是作线段所在的直线互相垂直,或作射线
所在的直线的垂线,因为射线和线段都是直线的一部
分.在垂线的画法中,有时需延长线段,垂足在延长
线上,并记上直角符号“﹁”.
合作探究
注意:画垂线也可用以下两种方法:
(1)利用量角器画;(2)用折叠法画.
例3
如图,M是三角形ABC中BC边上的任意一点,请
你按照下列要求画图:
(1)过M点画直线AB的垂线m;
(2)过M点画直线BC的垂线n;
(3)过M点画直线AC的垂线p.
导引:观察图形不难看出,(1)(3)属于过直线外一点画
已知直线的垂线,(2)属于过直线上一点画已知
直线的垂线,所以按照“一靠、二过、三画”
的方法画图即可.
解:画出的直线m,n,p如上页图.
过已知点画已知直线的垂线,实际上就是过已知
点画一条直线,使所画直线与已知直线相交所成的角
是90°.
新知小结
过一条线段外一点,作这条线段的垂线,垂足
在( )
A.这条线段上
B.这条线段的端点处
C.这条线段的延长线上
D.以上都有可能
1
D
巩固新知
3
知识点
垂线的性质
探究
如图.
(1)用三角尺或量角器画已知直线l的垂线,这样的垂线能画出几条?
(2)经过直线l上一点A画l的垂线,这样的垂线能画出几条?
(3)经过直线l外一点B画l的垂线,这样的垂线能画出几条?
合作探究
经过一点(已知直线上或直线外),能画出已知直
线的一条垂线,并且只
能画出一条垂线.即
在同一平面内,过一点有且只有一条直线与已知
直线垂直.
新知小结
在平面内,不是在空间内,这是需要注意的条件:
其中,一点可以是直线上一点也可以是直线外一点;
“有且只有”中的“有”是指能画出一条已知直线的
垂线,即存在性,“只有”是指只能画一条,即唯
一性.
例4〈厦门〉如图,已知直线AB,CB,l在同一平面内,
若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合
题意的图形可以是( )
C
合作探究
导引:根据题意可知,过点B有AB,CB都与直线l垂直,
由垂线的性质可知,在同一平面内,过一点有且
只有一条直线与已知直线垂直,所以A、B、C三
点在一条直线上.
利用直线的性质解答题目,要注意直线性质满足的条件:
1.
在平面内;
2.
过一点,点的位置可以在直线上也可以在直线外;
3.
相交所成的角必须是直角,以上三条缺一不可.
新知小结
在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
1
C
巩固新知
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只
有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已
知直线垂直
D.两点之间,线段最短
2
C
以下几个方面由学生自己总结:
①
垂线的定义及垂直的符号表示;
②
垂线的有关性质;
③
过一点作已知直线的垂线的方法.
1
知识小结
归纳新知
(1)在图①中,过AB外一点M作AB的垂线;
(2)在图②中,过点A,B分别作OB,OA的垂线.
2
易错小结
解:
(1)如图①所示.
(2)如图②所示.
本题易错之处在于误认为垂足一定落在线段或射线上.
易错点:误认为垂足一定要在线段或射线上而导致
错误.
互相垂直
AB⊥CD
∠AOC=∠BOC=∠BOD=∠AOD=90°
课后练习
B
C
B
D
用三角尺的一条直角边靠在已知直线上
使已知点落在另一条直角边上
过已知点画出与已知直线垂直的直线
C
有且只有
上
存在
唯一
D
B
【答案】A
再见
