人教版(2019)高一物理必修第二册第六章圆周运动单元测试卷
文档属性
| 名称 | 人教版(2019)高一物理必修第二册第六章圆周运动单元测试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 154.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-19 16:47:18 | ||
图片预览




文档简介
第六章《圆周运动》单元测试卷
一、单选题(共15小题)
1.如图所示,长为L的细绳的一端固定于O点,另一端系一个小球,在O点的正下方钉一个光滑的小钉子A,小球从一定高度摆下,当细绳与钉子相碰时,钉子的位置距小球,则细绳碰到钉子前、后瞬间( )
A.
绳对小球的拉力之比为1∶4
B.
小球所受合外力之比为1∶4
C.
小球做圆周运动的线速度之比为1∶4
D.
小球做圆周运动的角速度之比为4∶1
2.如图所示,质量相等的a、b两物体放在圆盘上,到圆心的距离之比是2∶3,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止,a、b两物体做圆周运动的向心力之比是( )
A.
1∶1
B.
3∶2
C.
2∶3
D.
9∶4
3.如图所示,工厂里的吊车正吊着一个铸件沿水平方向匀速运动,因为某种原因,突然紧急刹车,此瞬时铸件所受的合外力(
)
A.
为零
B.
方向向前
C.
方向竖直向上
D.
方向竖直向下
4.如图所示为一种早期的自行车,这种不带链条传动的自行车前轮的直径很大,这样的设计在当时主要是为了( ).
A.
提高速度
B.
提高稳定性
C.
骑行方便
D.
减小阻力
5.汽车在水平公路上转弯时,提供汽车所需向心力的是( )
A.
汽车的重力
B.
路面对汽车的支持力
C.
汽车的重力与路面对汽车支持力的合力
D.
路面对汽车的静摩擦力
6.下列对圆锥摆的受力分析正确的是( )
A.
B.
C.
D.
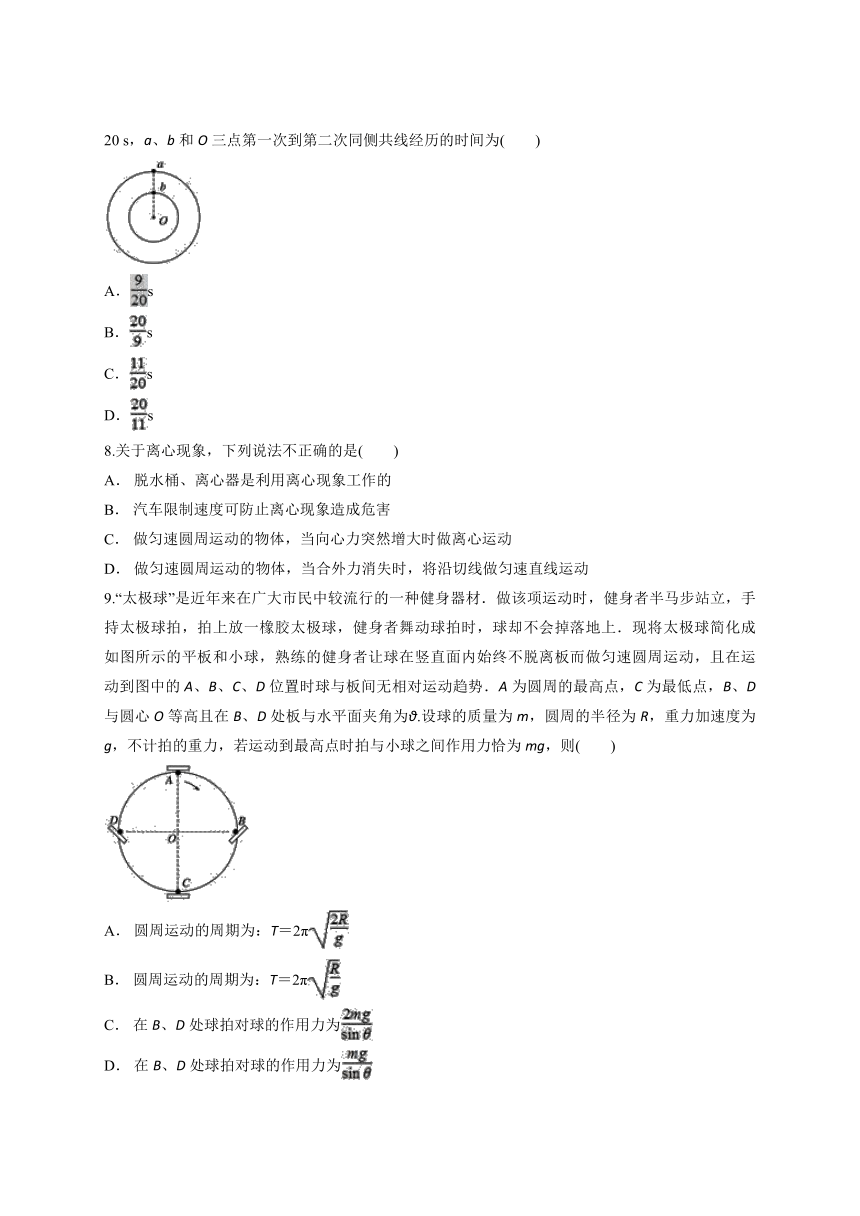
7.如图,两质点a、b在同一平面内绕O沿逆时针方向做匀速圆周运动,a、b的周期分别为2
s和20
s,a、b和O三点第一次到第二次同侧共线经历的时间为( )
A.s
B.s
C.s
D.s
8.关于离心现象,下列说法不正确的是( )
A.
脱水桶、离心器是利用离心现象工作的
B.
汽车限制速度可防止离心现象造成危害
C.
做匀速圆周运动的物体,当向心力突然增大时做离心运动
D.
做匀速圆周运动的物体,当合外力消失时,将沿切线做匀速直线运动
9.“太极球”是近年来在广大市民中较流行的一种健身器材.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高且在B、D处板与水平面夹角为θ.设球的质量为m,圆周的半径为R,重力加速度为g,不计拍的重力,若运动到最高点时拍与小球之间作用力恰为mg,则( )
A.
圆周运动的周期为:T=2π
B.
圆周运动的周期为:T=2π
C.
在B、D处球拍对球的作用力为
D.
在B、D处球拍对球的作用力为
10.如图所示,自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样,它们的边缘上有三个点A,B,C.下列关于它们的线速度大小、角速度、周期、向心加速度大小关系式中正确的是( )
A.vA>vB>vC
B.ωA<ωB<ωC
C.TA>TB>TC
D.aA<aB<aC
11.如图所示,小球从“离心轨道”上滑下,若小球经过A点时开始脱离圆环,则小球将做( )
A.
自由落体运动
B.
平抛运动
C.
斜上抛运动
D.
竖直上抛运动
12.如图所示为自行车的传动装置,大齿盘通过链条带动小齿盘转动时,大齿盘边缘的线速度v1和小齿盘边缘的线速度v2的大小关系是( )
A.v1>v2
B.v1=v2
C.v1<v2
D.
不能确定
13.如图所示,在风力推动下,风叶带动发电机发电,M、N为同一个叶片上的两点,下列说法中正确的是( )
A.M点的线速度等于N点的线速度
B.M点的角速度小于N点的角速度
C.M点的向心加速度小于N点的向心加速度
D.M点的周期大于N点的周期
14.如下图所示,一种向自行车车灯供电的小发电机的上端有一半径R0=1.0
cm的摩擦小轮,小轮与自行车车轮的边缘接触.当车轮转动时,因摩擦而带动小轮转动,从而为发电机提供动力.自行车车轮的半径R1=35
cm,小齿轮的半径R2=4.0
cm,大齿轮的半径R3=10.0
cm.则大齿轮的转速n1和摩擦小轮的转速n2之比为(假定摩擦小轮与自行车车轮之间无相对滑动)( )
A.
2∶175
B.
1∶175
C.
4∶175
D.
1∶140
15.如图所示,在匀速转动的圆筒内壁上,有一物体随圆筒一起转动而未滑动.当圆筒的角速度ω增大以后,下列说法正确的是( )
A.
物体所受弹力增大,摩擦力也增大了
B.
物体所受弹力增大,摩擦力减小了
C.
物体所受弹力和摩擦力都减小了
D.
物体所受弹力增大,摩擦力不变
二、填空题(共3小题)
16.如图所示,质量为1
t的汽车驶上一个半径为50
m的圆形拱桥,当它到达桥顶(A点)时的速度为5
m/s,此时车对桥面的压力为________N.此时汽车处于________(填“超重”或“失重”)状态.(g=10
m/s2)
若汽车接下去行驶遇到一段水平路面和凹形桥面,则在A、B、C三点中,司机为防止爆胎,需要在到达________(填“A”或“B”或“C”)点前提前减速;为了防止汽车腾空离地,需要在到达________(填“A”或“B”或“C”)点前提前减速.
17.在圆轨道上稳定运行的飞船内,宇航员为了验证向心力公式,设计了如图所示的装置(图中O为光滑的小孔):给待测物体一个初速度,使它在水平光滑桌面上做匀速圆周运动.该飞船内具有基本测量工具.
(1)实验时需要测量的物理量是_____________(写出描述物理量的文字和符号)
(2)若向心力公式成立,则上述物理量的关系是:__________.
18.飞机由俯冲转为拉起的一段轨迹可看成一段圆弧,如图所示,飞机做俯冲拉起运动时,在最低点附近做半径为r=180
m的圆周运动,如果飞行员质量m=70
kg,飞机经过最低点P时的速度v=360
km/h,则这时飞行员对座椅的压力是________.(g取10
m/s2)
三、实验题(共3小题)
19.一物理兴趣小组利用学校实验室的数字实验系统探究物体做圆周运动时向心力大小与角速度、半径的关系.在保证重物的质量m和做圆周运动的角速度ω不变的情况下,改变重物做圆周运动的半径r,得到几组向心力大小F与半径r的数据,记录到表1中.
表1 力F与半径r的测量数据
在保证重物的质量m和做圆周运动的半径r不变的情况下,改变重物的角速度ω得到几组力F和角速度ω的数据,记录到表2中.
表2 力F与角速度ω的测量数据
(1)根据上面的测量结果,分别在下图中作出F-r图线和F-ω图线.
(2)若作出的F-ω图线不是直线,可以尝试作F-ω2图线,试在图中作出F-ω2图线.
(3)通过以上实验探究可知,向心力与转动半径成________,与角速度的平方成________.
20.用如图所示的装置可以探究做匀速圆周运动的物体需要的向心力的大小与哪些因素有关.
(1)本实验采用的科学方法是________.
A.控制变量法
B.累积法
C.微元法
D.放大法
(2)图示情景正在探究的是________.
A.向心力的大小与半径的关系
B.向心力的大小与线速度大小的关系
C.向心力的大小与角速度大小的关系
D.向心力的大小与物体质量的关系
(3)通过本实验可以得到的结果是________.
A.在质量和半径一定的情况下,向心力的大小与角速度成正比
B.在质量和半径一定的情况下,向心力的大小与线速度的大小成正比
C.在半径和角速度一定的情况下,向心力的大小与质量成正比
D.在质量和角速度一定的情况下,向心力的大小与半径成反比
21.如图甲所示为测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机转轴上,在电动机的带动下匀速转动.在圆形卡纸的旁边垂直安装一个改装了的电火花计时器.(电火花计时器每隔相同的时间间隔打一个点)
(1)请将下列实验步骤按先后排序:________.
①使电火花计时器与圆形卡纸保持良好接触
②接通电火花计时器的电源,使它工作起来
③启动电动机,使圆形卡纸转动起来
④关闭电动机,拆除电火花计时器;研究卡纸上留下的一段点迹(如图乙所示),写出角速度ω的表达式,代入数据,得出ω的测量值.
(2)要得到角速度ω的测量值,还缺少一种必要的测量工具,它是________.
A.秒表 B.毫米刻度尺 C.圆规 D.量角器
(3)为了避免在卡纸连续转动的过程中出现打点重叠,在电火花计时器与盘面保持良好接触的同时,可以缓慢地将电火花计时器沿圆形卡纸半径方向向卡纸中心移动.则卡纸上打下的点的分布曲线不是一个圆,而是类似一种螺旋线,如图丙所示.这对测量结果________(填“有”或“无”)影响.
四、计算题(共3小题)
22.如图所示,用一根长为l=1
m的细线,一端系一质量为m=1
kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT.(g取10
m/s2,结果可用根式表示)求:
(1)若要小球离开锥面,则小球的角速度ω0至少为多大.
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大.
23.如图所示,水平转盘可绕竖直中心轴转动,盘上叠放着质量均为1
kg的A、B两个物块,B物块用长为0.25
m的细线与固定在转盘中心处的力传感器相连,两个物块和传感器的大小均可不计.细线能承受的最大拉力为8
N,A、B间的动摩擦因数为0.4,B与转盘间的动摩擦因数为0.1,且可认为最大静摩擦力等于滑动摩擦力.转盘静止时,细线刚好伸直,传感器的读数为零.当转盘以不同的角速度匀速转动时,传感器上就会显示相应的读数F(g=10
m/s2).
(1)当B与盘面之间的静摩擦力达到最大值时,求F的大小和转盘的角速度ω1;
(2)当A与B恰好分离时,求F的大小和转盘的角速度ω2;
(3)试通过计算在坐标系中作出F-ω2图象.
24.做匀速圆周运动的物体,10
s内沿半径为20
m的圆周运动100
m,试求物体做匀速圆周运动时:
(1)线速度的大小;
(2)角速度的大小;
(3)周期的大小.
答案解析
1.【答案】B
2.【答案】C
3.【答案】C
【解析】因为在刹车一瞬间,铸件还没来得及发生位置变化,所以物体的运动变为圆周运动,需要向心力,所以绳子的拉力减去重力的合力提供向心力,向心力是指向圆心的合力.所以合力方向竖直向上.故选C.
4.【答案】A
【解析】在骑车人脚蹬车轮转速一定的情况下,据公式v=ωr知,轮子半径越大,车轮边缘的线速度越大,车行驶得也就越快,故A选项正确.
5.【答案】D
【解析】汽车在水平公路上拐弯,重力和支持力平衡,靠静摩擦力提供圆周运动的向心力,故D正确.
6.【答案】D
【解析】圆锥摆向心力由合外力提供,方向指向圆周运动的圆心,D对.
7.【答案】B
【解析】再次共线时,运动过程转过的圆心角之差为π,则ωat-ωbt=π,t=s
8.【答案】C
【解析】脱水桶、离心器都是利用离心现象工作的,A正确.汽车限制速度,使得需要的向心力小于最大静摩擦力,可防止离心现象,B正确;做匀速圆周运动的物体,当提供的向心力突然增大时,做近心运动,而不是离心运动,C错误.匀速圆周运动的物体,当合外力消失时,将沿切线做匀速直线运动,D正确.
9.【答案】C
【解析】在最高点,根据牛顿第二定律得:mg+mg=m,解得:v=,则周期为:T===π,故A、B错误;球做匀速圆周运动,在B、D处,根据合外力提供向心力,结合几何关系得:sinθ=,解得:F==,故C正确,D错误.
10.【答案】D
【解析】由于A、B两点为共线关系,因此vA=vB,选项A错误;由于B、C两点为共轴关系,角速度相同,因此ωB=ωC,选项B错误;由T==,可判断选项C错误;由向心加速度a==ω2r可知选项D正确.
11.【答案】C
【解析】小球在脱离轨道时的速度是沿着轨道的切线方向的,即斜向上。当脱离轨道后小球只受重力,所以小球将做斜上抛运动。
12.【答案】B
【解析】同一皮带上线速度相等,同一转盘上角速度相等.在本题中,大齿盘边缘的线速度和小齿盘边缘的线速度相等,即有:v1=v2,故B正确.
13.【答案】C
【解析】由于M、N两点的转动的角速度相等,则周期相等,根据v=rω知,M点转动的半径小,则M点的线速度小于N点的线速度.故A、B、D错误.
根据a=rω2知,M、N的角速度相等,M点的转动半径小,则M点的向心加速度小于N点的向心加速度.故C正确.
故选:C.
14.【答案】A
【解析】
15.【答案】D
【解析】物体在竖直方向上受重力G与摩擦力Ff,是一对平衡力,在向心力方向上受弹力FN.根据向心力公式,可知FN=mω2R,当ω增大时,FN增大,所以应选D.
16.【答案】9
500 失重 C A
【解析】
17.【答案】(1)弹簧弹力F、物体质量m、物块转n圈时间t、轨道半径r (2)F=m()2r
【解析】据题,物体在桌面上做匀速圆周运动,物体与桌面间的摩擦力忽略不计,由弹簧秤的拉力提供物体的向心力.根据牛顿第二定律得:F=m()2r所以实验时需要测量的物理量是弹簧秤示数F、物块质量m、物块到小孔O的距离r、物块转n圈时间t.
18.【答案】4
589
N
【解析】飞机经过最低点时,v=360
km/h=100
m/s.
对飞行员进行受力分析,飞行员在竖直面内共受到重力G和座椅的支持力FN两个力的作用,根据牛顿第二定律得FN-mg=m,所以FN=mg+m=70×10
N+70×N≈4
589
N,由牛顿第三定律得,飞行员对座椅的压力为4
589
N.
19.【答案】(1)
(2)
(3)正比 正比
【解析】
20.【答案】(1)A (2)D (3)C
【解析】(1)在题图装置中,控制半径、角速度不变,只改变质量,来研究向心力大小与质量之间的关系,故采用控制变量法,A正确.(2)控制半径、角速度不变,只改变质量,来研究向心力大小与质量之间的关系,D正确.(3)通过控制变量法,得到的结果为在半径和角速度一定的情况下,向心力的大小与质量成正比,C正确.
21.【答案】(1)①③②④ (2)D (3)无
【解析】(1)该实验先将电火花计时器与圆形卡纸保持良好接触,先使卡片转动,再打点,最后取出卡片进行数据处理,故次序为①③②④.
(2)要测出角速度,需要测量点跟点间的角度,需要的器材是量角器.故选D.
(3)由于点跟点之间的角度没变化,则对测量角速度不影响.
22.【答案】1)rad/s (2)2rad/s
【解析】(1)若要小球刚好离开锥面,则小球只受到重力和细线的拉力,如图所示.
小球做匀速圆周运动的轨迹圆在水平面内,故向心力水平,运用牛顿第二定律及向心力公式得:
mgtanθ=mωlsinθ
解得:ω=
即ω0==rad/s.
(2)当细线与竖直方向成60°角时,由牛顿第二定律及向心力公式得:mgtanα=mω′2lsinα
解得:ω′2=,
即ω′==2rad/s.
23.【答案】(1)F=0 0≤ω≤2
rad/s (2)F=6
N ω2=4
rad/s
(3)
24.【答案】(1)10
m/s (2)0.5
rad/s (3)4π
s
一、单选题(共15小题)
1.如图所示,长为L的细绳的一端固定于O点,另一端系一个小球,在O点的正下方钉一个光滑的小钉子A,小球从一定高度摆下,当细绳与钉子相碰时,钉子的位置距小球,则细绳碰到钉子前、后瞬间( )
A.
绳对小球的拉力之比为1∶4
B.
小球所受合外力之比为1∶4
C.
小球做圆周运动的线速度之比为1∶4
D.
小球做圆周运动的角速度之比为4∶1
2.如图所示,质量相等的a、b两物体放在圆盘上,到圆心的距离之比是2∶3,圆盘绕圆心做匀速圆周运动,两物体相对圆盘静止,a、b两物体做圆周运动的向心力之比是( )
A.
1∶1
B.
3∶2
C.
2∶3
D.
9∶4
3.如图所示,工厂里的吊车正吊着一个铸件沿水平方向匀速运动,因为某种原因,突然紧急刹车,此瞬时铸件所受的合外力(
)
A.
为零
B.
方向向前
C.
方向竖直向上
D.
方向竖直向下
4.如图所示为一种早期的自行车,这种不带链条传动的自行车前轮的直径很大,这样的设计在当时主要是为了( ).
A.
提高速度
B.
提高稳定性
C.
骑行方便
D.
减小阻力
5.汽车在水平公路上转弯时,提供汽车所需向心力的是( )
A.
汽车的重力
B.
路面对汽车的支持力
C.
汽车的重力与路面对汽车支持力的合力
D.
路面对汽车的静摩擦力
6.下列对圆锥摆的受力分析正确的是( )
A.
B.
C.
D.
7.如图,两质点a、b在同一平面内绕O沿逆时针方向做匀速圆周运动,a、b的周期分别为2
s和20
s,a、b和O三点第一次到第二次同侧共线经历的时间为( )
A.s
B.s
C.s
D.s
8.关于离心现象,下列说法不正确的是( )
A.
脱水桶、离心器是利用离心现象工作的
B.
汽车限制速度可防止离心现象造成危害
C.
做匀速圆周运动的物体,当向心力突然增大时做离心运动
D.
做匀速圆周运动的物体,当合外力消失时,将沿切线做匀速直线运动
9.“太极球”是近年来在广大市民中较流行的一种健身器材.做该项运动时,健身者半马步站立,手持太极球拍,拍上放一橡胶太极球,健身者舞动球拍时,球却不会掉落地上.现将太极球简化成如图所示的平板和小球,熟练的健身者让球在竖直面内始终不脱离板而做匀速圆周运动,且在运动到图中的A、B、C、D位置时球与板间无相对运动趋势.A为圆周的最高点,C为最低点,B、D与圆心O等高且在B、D处板与水平面夹角为θ.设球的质量为m,圆周的半径为R,重力加速度为g,不计拍的重力,若运动到最高点时拍与小球之间作用力恰为mg,则( )
A.
圆周运动的周期为:T=2π
B.
圆周运动的周期为:T=2π
C.
在B、D处球拍对球的作用力为
D.
在B、D处球拍对球的作用力为
10.如图所示,自行车的大齿轮、小齿轮、后轮三个轮子的半径不一样,它们的边缘上有三个点A,B,C.下列关于它们的线速度大小、角速度、周期、向心加速度大小关系式中正确的是( )
A.vA>vB>vC
B.ωA<ωB<ωC
C.TA>TB>TC
D.aA<aB<aC
11.如图所示,小球从“离心轨道”上滑下,若小球经过A点时开始脱离圆环,则小球将做( )
A.
自由落体运动
B.
平抛运动
C.
斜上抛运动
D.
竖直上抛运动
12.如图所示为自行车的传动装置,大齿盘通过链条带动小齿盘转动时,大齿盘边缘的线速度v1和小齿盘边缘的线速度v2的大小关系是( )
A.v1>v2
B.v1=v2
C.v1<v2
D.
不能确定
13.如图所示,在风力推动下,风叶带动发电机发电,M、N为同一个叶片上的两点,下列说法中正确的是( )
A.M点的线速度等于N点的线速度
B.M点的角速度小于N点的角速度
C.M点的向心加速度小于N点的向心加速度
D.M点的周期大于N点的周期
14.如下图所示,一种向自行车车灯供电的小发电机的上端有一半径R0=1.0
cm的摩擦小轮,小轮与自行车车轮的边缘接触.当车轮转动时,因摩擦而带动小轮转动,从而为发电机提供动力.自行车车轮的半径R1=35
cm,小齿轮的半径R2=4.0
cm,大齿轮的半径R3=10.0
cm.则大齿轮的转速n1和摩擦小轮的转速n2之比为(假定摩擦小轮与自行车车轮之间无相对滑动)( )
A.
2∶175
B.
1∶175
C.
4∶175
D.
1∶140
15.如图所示,在匀速转动的圆筒内壁上,有一物体随圆筒一起转动而未滑动.当圆筒的角速度ω增大以后,下列说法正确的是( )
A.
物体所受弹力增大,摩擦力也增大了
B.
物体所受弹力增大,摩擦力减小了
C.
物体所受弹力和摩擦力都减小了
D.
物体所受弹力增大,摩擦力不变
二、填空题(共3小题)
16.如图所示,质量为1
t的汽车驶上一个半径为50
m的圆形拱桥,当它到达桥顶(A点)时的速度为5
m/s,此时车对桥面的压力为________N.此时汽车处于________(填“超重”或“失重”)状态.(g=10
m/s2)
若汽车接下去行驶遇到一段水平路面和凹形桥面,则在A、B、C三点中,司机为防止爆胎,需要在到达________(填“A”或“B”或“C”)点前提前减速;为了防止汽车腾空离地,需要在到达________(填“A”或“B”或“C”)点前提前减速.
17.在圆轨道上稳定运行的飞船内,宇航员为了验证向心力公式,设计了如图所示的装置(图中O为光滑的小孔):给待测物体一个初速度,使它在水平光滑桌面上做匀速圆周运动.该飞船内具有基本测量工具.
(1)实验时需要测量的物理量是_____________(写出描述物理量的文字和符号)
(2)若向心力公式成立,则上述物理量的关系是:__________.
18.飞机由俯冲转为拉起的一段轨迹可看成一段圆弧,如图所示,飞机做俯冲拉起运动时,在最低点附近做半径为r=180
m的圆周运动,如果飞行员质量m=70
kg,飞机经过最低点P时的速度v=360
km/h,则这时飞行员对座椅的压力是________.(g取10
m/s2)
三、实验题(共3小题)
19.一物理兴趣小组利用学校实验室的数字实验系统探究物体做圆周运动时向心力大小与角速度、半径的关系.在保证重物的质量m和做圆周运动的角速度ω不变的情况下,改变重物做圆周运动的半径r,得到几组向心力大小F与半径r的数据,记录到表1中.
表1 力F与半径r的测量数据
在保证重物的质量m和做圆周运动的半径r不变的情况下,改变重物的角速度ω得到几组力F和角速度ω的数据,记录到表2中.
表2 力F与角速度ω的测量数据
(1)根据上面的测量结果,分别在下图中作出F-r图线和F-ω图线.
(2)若作出的F-ω图线不是直线,可以尝试作F-ω2图线,试在图中作出F-ω2图线.
(3)通过以上实验探究可知,向心力与转动半径成________,与角速度的平方成________.
20.用如图所示的装置可以探究做匀速圆周运动的物体需要的向心力的大小与哪些因素有关.
(1)本实验采用的科学方法是________.
A.控制变量法
B.累积法
C.微元法
D.放大法
(2)图示情景正在探究的是________.
A.向心力的大小与半径的关系
B.向心力的大小与线速度大小的关系
C.向心力的大小与角速度大小的关系
D.向心力的大小与物体质量的关系
(3)通过本实验可以得到的结果是________.
A.在质量和半径一定的情况下,向心力的大小与角速度成正比
B.在质量和半径一定的情况下,向心力的大小与线速度的大小成正比
C.在半径和角速度一定的情况下,向心力的大小与质量成正比
D.在质量和角速度一定的情况下,向心力的大小与半径成反比
21.如图甲所示为测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机转轴上,在电动机的带动下匀速转动.在圆形卡纸的旁边垂直安装一个改装了的电火花计时器.(电火花计时器每隔相同的时间间隔打一个点)
(1)请将下列实验步骤按先后排序:________.
①使电火花计时器与圆形卡纸保持良好接触
②接通电火花计时器的电源,使它工作起来
③启动电动机,使圆形卡纸转动起来
④关闭电动机,拆除电火花计时器;研究卡纸上留下的一段点迹(如图乙所示),写出角速度ω的表达式,代入数据,得出ω的测量值.
(2)要得到角速度ω的测量值,还缺少一种必要的测量工具,它是________.
A.秒表 B.毫米刻度尺 C.圆规 D.量角器
(3)为了避免在卡纸连续转动的过程中出现打点重叠,在电火花计时器与盘面保持良好接触的同时,可以缓慢地将电火花计时器沿圆形卡纸半径方向向卡纸中心移动.则卡纸上打下的点的分布曲线不是一个圆,而是类似一种螺旋线,如图丙所示.这对测量结果________(填“有”或“无”)影响.
四、计算题(共3小题)
22.如图所示,用一根长为l=1
m的细线,一端系一质量为m=1
kg的小球(可视为质点),另一端固定在一光滑锥体顶端,锥面与竖直方向的夹角θ=37°,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为ω时,细线的张力为FT.(g取10
m/s2,结果可用根式表示)求:
(1)若要小球离开锥面,则小球的角速度ω0至少为多大.
(2)若细线与竖直方向的夹角为60°,则小球的角速度ω′为多大.
23.如图所示,水平转盘可绕竖直中心轴转动,盘上叠放着质量均为1
kg的A、B两个物块,B物块用长为0.25
m的细线与固定在转盘中心处的力传感器相连,两个物块和传感器的大小均可不计.细线能承受的最大拉力为8
N,A、B间的动摩擦因数为0.4,B与转盘间的动摩擦因数为0.1,且可认为最大静摩擦力等于滑动摩擦力.转盘静止时,细线刚好伸直,传感器的读数为零.当转盘以不同的角速度匀速转动时,传感器上就会显示相应的读数F(g=10
m/s2).
(1)当B与盘面之间的静摩擦力达到最大值时,求F的大小和转盘的角速度ω1;
(2)当A与B恰好分离时,求F的大小和转盘的角速度ω2;
(3)试通过计算在坐标系中作出F-ω2图象.
24.做匀速圆周运动的物体,10
s内沿半径为20
m的圆周运动100
m,试求物体做匀速圆周运动时:
(1)线速度的大小;
(2)角速度的大小;
(3)周期的大小.
答案解析
1.【答案】B
2.【答案】C
3.【答案】C
【解析】因为在刹车一瞬间,铸件还没来得及发生位置变化,所以物体的运动变为圆周运动,需要向心力,所以绳子的拉力减去重力的合力提供向心力,向心力是指向圆心的合力.所以合力方向竖直向上.故选C.
4.【答案】A
【解析】在骑车人脚蹬车轮转速一定的情况下,据公式v=ωr知,轮子半径越大,车轮边缘的线速度越大,车行驶得也就越快,故A选项正确.
5.【答案】D
【解析】汽车在水平公路上拐弯,重力和支持力平衡,靠静摩擦力提供圆周运动的向心力,故D正确.
6.【答案】D
【解析】圆锥摆向心力由合外力提供,方向指向圆周运动的圆心,D对.
7.【答案】B
【解析】再次共线时,运动过程转过的圆心角之差为π,则ωat-ωbt=π,t=s
8.【答案】C
【解析】脱水桶、离心器都是利用离心现象工作的,A正确.汽车限制速度,使得需要的向心力小于最大静摩擦力,可防止离心现象,B正确;做匀速圆周运动的物体,当提供的向心力突然增大时,做近心运动,而不是离心运动,C错误.匀速圆周运动的物体,当合外力消失时,将沿切线做匀速直线运动,D正确.
9.【答案】C
【解析】在最高点,根据牛顿第二定律得:mg+mg=m,解得:v=,则周期为:T===π,故A、B错误;球做匀速圆周运动,在B、D处,根据合外力提供向心力,结合几何关系得:sinθ=,解得:F==,故C正确,D错误.
10.【答案】D
【解析】由于A、B两点为共线关系,因此vA=vB,选项A错误;由于B、C两点为共轴关系,角速度相同,因此ωB=ωC,选项B错误;由T==,可判断选项C错误;由向心加速度a==ω2r可知选项D正确.
11.【答案】C
【解析】小球在脱离轨道时的速度是沿着轨道的切线方向的,即斜向上。当脱离轨道后小球只受重力,所以小球将做斜上抛运动。
12.【答案】B
【解析】同一皮带上线速度相等,同一转盘上角速度相等.在本题中,大齿盘边缘的线速度和小齿盘边缘的线速度相等,即有:v1=v2,故B正确.
13.【答案】C
【解析】由于M、N两点的转动的角速度相等,则周期相等,根据v=rω知,M点转动的半径小,则M点的线速度小于N点的线速度.故A、B、D错误.
根据a=rω2知,M、N的角速度相等,M点的转动半径小,则M点的向心加速度小于N点的向心加速度.故C正确.
故选:C.
14.【答案】A
【解析】
15.【答案】D
【解析】物体在竖直方向上受重力G与摩擦力Ff,是一对平衡力,在向心力方向上受弹力FN.根据向心力公式,可知FN=mω2R,当ω增大时,FN增大,所以应选D.
16.【答案】9
500 失重 C A
【解析】
17.【答案】(1)弹簧弹力F、物体质量m、物块转n圈时间t、轨道半径r (2)F=m()2r
【解析】据题,物体在桌面上做匀速圆周运动,物体与桌面间的摩擦力忽略不计,由弹簧秤的拉力提供物体的向心力.根据牛顿第二定律得:F=m()2r所以实验时需要测量的物理量是弹簧秤示数F、物块质量m、物块到小孔O的距离r、物块转n圈时间t.
18.【答案】4
589
N
【解析】飞机经过最低点时,v=360
km/h=100
m/s.
对飞行员进行受力分析,飞行员在竖直面内共受到重力G和座椅的支持力FN两个力的作用,根据牛顿第二定律得FN-mg=m,所以FN=mg+m=70×10
N+70×N≈4
589
N,由牛顿第三定律得,飞行员对座椅的压力为4
589
N.
19.【答案】(1)
(2)
(3)正比 正比
【解析】
20.【答案】(1)A (2)D (3)C
【解析】(1)在题图装置中,控制半径、角速度不变,只改变质量,来研究向心力大小与质量之间的关系,故采用控制变量法,A正确.(2)控制半径、角速度不变,只改变质量,来研究向心力大小与质量之间的关系,D正确.(3)通过控制变量法,得到的结果为在半径和角速度一定的情况下,向心力的大小与质量成正比,C正确.
21.【答案】(1)①③②④ (2)D (3)无
【解析】(1)该实验先将电火花计时器与圆形卡纸保持良好接触,先使卡片转动,再打点,最后取出卡片进行数据处理,故次序为①③②④.
(2)要测出角速度,需要测量点跟点间的角度,需要的器材是量角器.故选D.
(3)由于点跟点之间的角度没变化,则对测量角速度不影响.
22.【答案】1)rad/s (2)2rad/s
【解析】(1)若要小球刚好离开锥面,则小球只受到重力和细线的拉力,如图所示.
小球做匀速圆周运动的轨迹圆在水平面内,故向心力水平,运用牛顿第二定律及向心力公式得:
mgtanθ=mωlsinθ
解得:ω=
即ω0==rad/s.
(2)当细线与竖直方向成60°角时,由牛顿第二定律及向心力公式得:mgtanα=mω′2lsinα
解得:ω′2=,
即ω′==2rad/s.
23.【答案】(1)F=0 0≤ω≤2
rad/s (2)F=6
N ω2=4
rad/s
(3)
24.【答案】(1)10
m/s (2)0.5
rad/s (3)4π
s
